Compétition de saut d’obstacles en Hobby Horse

Asie septembre 2025 Sujet 2

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°25-PYCPE4

Sujet et corrigé

EXERCICE 1 – COMPÉTITION DE SAUT D’OBSTACLES EN HOBBY HORSE (11 POINTS)

D’après https://www.hobbyhorseland.com/blog/hobby-horsing-tout-savoir-sur-ce-sport-n7

Cet exercice comporte trois parties indépendantes. L’objectif de la première partie est de déterminer par effet Doppler la vitesse du véhicule annonçant la compétition grâce à l’effet Doppler.

L’objectif de la deuxième partie est de déterminer la qualité du crin synthétique du hobby horse par le phénomène de diffraction.

L’objectif de la dernière partie est de déterminer les paramètres permettant d’améliorer le saut d’obstacle par une étude dynamique et cinématique.

1.    Annonce de la compétition de hobby horse diffusée par le mégaphone d’une voiture.

Pour diffuser l’information de la tenue de la compétition de saut d’obstacles en hobby horse, une voiture munie d’un mégaphone sillonne les rues de la ville dans laquelle l’évènement se déroule. En début d’annonce, une note est jouée pour capter l’attention des auditeurs.

La voiture s’approche d’un citadin qui se trouve immobile sur le bord de la route. Ce dernier perçoit la fréquence sonore f_R de la note diffusée par le mégaphone vérifiant la relation :

$$f_R = \frac{v_{son}}{v_{son} – v}\cdot f_E$$

• f_E est la fréquence de l’onde sonore émise par le mégaphone ;
• v est la valeur de la vitesse du véhicule qui se rapproche du citadin (par rapport à celui-ci) ;
• v_son est la célérité du son dans l’air, considérée égale à 340 m∙s^–1.

Q1. Décrire l’effet Doppler.

Une onde émise avec une fréquence $f_e$ est perçue avec une fréquence $f_r$ différente de $f_e$ lorsque l’émetteur et le récepteur sont en déplacement relatif : c’est l’effet Doppler.

Q2. À partir de la relation donnée pour la fréquence sonore perçue f_R, justifier que le son entendu par le citadin est plus aigu que celui qu’il percevrait si le véhicule était à l’arrêt.

$$f_R=\frac{v_{son}}{v_{son}-v}\times f_E$$

$v_{son}>v_{son}-v$
$$\Longrightarrow \frac{v_{son}}{v_{son}-v}>1$$
$$f_R=\frac{v_{son}}{v_{son}-v}\times f_E$$
$$f_R>f_E$$

La fréquence sonore perçue $f_R$ est supérieure à la fréquence sonore émise $f_E$ : La fréquence sonore perçue $f_R$ est donc plus aiguë que la fréquence sonore émise $f_E$.

Q3. En déduire la valeur de la vitesse v du véhicule sachant que le citadin perçoit un son de fréquence f_R = 448 Hz et que le mégaphone du véhicule en approche émet un son de fréquence f_E = 440 Hz. Indiquer si la voiture respecte ou non la vitesse maximale autorisée dans une zone limitée à 30 km∙h^–1.

$$f_R=\frac{v_{son}}{v_{son}-v}\times f_E$$

$$f_R\times (v_{son}-v)=v_{son}\times f_E$$
$$(v_{son}-v)=\frac{v_{son}\times f_E}{f_R}$$
$$v_{son}-v=\frac{v_{son}\times f_E}{f_R}$$
$$-v=\frac{v_{son}\times f_E}{f_R}-v_{son}$$
$$v=-\frac{v_{son}\times f_E}{f_R}+v_{son}$$
$$v=-\frac{340\times 440}{448}+340$$
$$v=6,07\ \text{m.s}^{-1}$$

2.   Préparation avant la compétition de hobby horse.

Certains hobby horses ont une crinière composée de crins synthétiques. Afin de comparer le diamètre des crins synthétiques utilisés à celui des crins de cheval, on réalise l’expérience de diffraction schématisée sur la figure 1.

On utilise une diode laser de longueur d’onde λ et un crin synthétique de diamètre a. Un écran est placé à une distance D du crin. La largeur L de la tache centrale de la figure de diffraction ainsi obtenue est mesurée directement sur l’écran.

θ est l’angle caractéristique de diffraction, de valeur très inférieure à un radian. Il a pour expression : $\theta = \frac{\lambda}{a}$

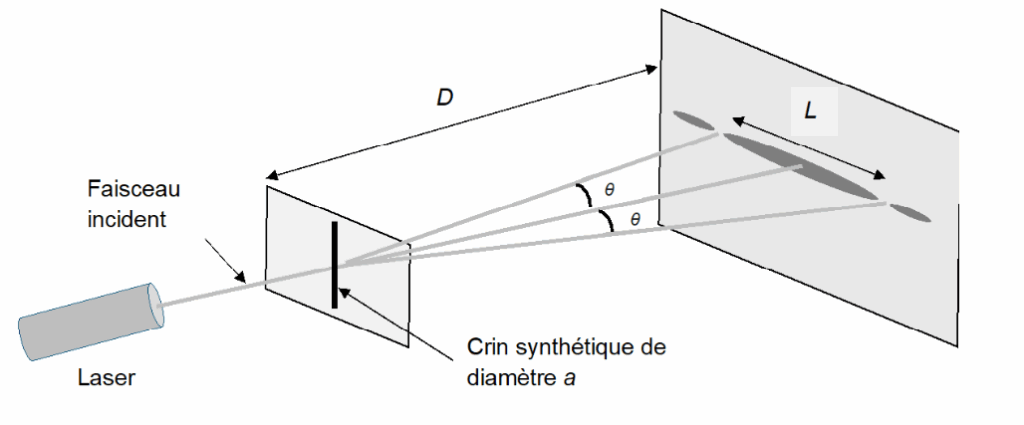
Figure 1. Schéma du montage de diffraction d’un faisceau laser par un crin synthétique.

Données :

• distance crin-écran D = 2,00 m et son incertitude-type u(D) = 0,01 m ;
• diode laser utilisée de longueur d’onde λ  = 650 nm et son incertitude-type u(λ) = 10 nm ;
• largeur  de  la  tache  centrale  mesurée  L = 1,80 cm  et son  incertitude-type u(L) = 0,05 cm ;
• on se place dans l’approximation des petits angles telle que tan θ ≈ θ.
• pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on utilise le quotient $\left|\frac{x-x_{ref}}{u\left(x\right)}\right|$ avec x, la valeur mesurée, x_réf la valeur de référence et u(x), l’incertitude-type associée à la valeur mesurée x.

Q4. À l’aide de la figure 1, établir l’expression du diamètre a du crin synthétique en fonction de λ, D et L.

$$\theta=\frac{\lambda}{a}$$

Lorsque $\theta$ est petit, on considère que $\tan(\theta)\approx\theta$ :

$$\tan(\theta)=\frac{d}{2D}$$
$$\theta=\frac{d}{2D}$$

$$\theta=\frac{\lambda}{a}$$
$$\theta=\frac{L}{2D}$$

$$\frac{L}{2D}=\frac{\lambda}{a}$$
$$a\times \frac{L}{2D}=\lambda$$
$$a=\frac{2D\times\lambda}{L}$$

Q5. À l’aide des données, montrer que la valeur du diamètre a du crin synthétique utilisé pour fabriquer la crinière du hobby horse est voisine de 144 μm.

$$a=\frac{2D\times\lambda}{L}$$
$$a=\frac{2\times 2{,}00\times 650\times10^{-9}}{1{,}80\times10^{-2}}$$
$$a=1{,}44\times10^{-4}\ \text{m}$$
$$a=144\times10^{-6}\ \text{m}$$
$$a=144\ \mu\text{m}$$

Q6. À l’aide des données, calculer la valeur de l’incertitude-type u(a) du diamètre du crin synthétique utilisé, donnée par la relation :

$$u\left(a\right)=a\times\sqrt{\left(\frac{u\left(\lambda\right)}{\lambda}\right)^2+\left(\frac{u\left(L\right)}{L}\right)^2+\left(\frac{u\left(D\right)}{D}\right)^2}$$

Préciser si le diamètre du crin synthétique choisi convient pour simuler le crin réel d’un cheval dont le diamètre de référence est égal à 140 μm.

$$u(a)=a\times\sqrt{\left(\frac{u(\lambda)}{\lambda}\right)^2+\left(\frac{u(L)}{L}\right)^2+\left(\frac{u(D)}{D}\right)^2}$$

$$u(a)=144\times10^{-6}\times\sqrt{\left(\frac{10\times10^{-9}}{650\times10^{-9}}\right)^2+\left(\frac{0{,}05\times10^{-2}}{1{,}80\times10^{-2}}\right)^2+\left(\frac{0{,}01}{2{,}00}\right)^2}$$
$$u(a)=5\times10^{-6}\ \text{m}$$
$$u(a)=5\ \mu\text{m}$$

Pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser :
$$z=\left|\frac{x-x_{ref}}{u(x)}\right|$$

Ici :
$$z=\left|\frac{140-144}{5}\right|$$
$$z=0,8$$

$z<2$ : la mesure est en accord avec la valeur de référence.
Donc le diamètre du crin synthétique convient.

3.   Étude cinématique du saut d’obstacles en hobby horse.

Le saut d’obstacles en hobby horse est une discipline qui se rapproche du saut de haies en athlétisme, mais avec une difficulté supplémentaire puisqu’il faut tenir d’une main le bâton et de l’autre les rênes, ce qui ne permet donc pas d’équilibrer le corps en utilisant les bras comme balancier.

On appellera hobbyhorseur le système {hobby horse + cavalier}. Ce système de masse m est modélisé par un point matériel assimilé à son centre de masse M. L’étude se fait dans le référentiel terrestre considéré comme galiléen.

À l’instant $t = 0$, le hobbyhorseur ne touche plus le sol, il est à la verticale du point $O$, engagé dans son saut par-dessus l’obstacle constitué par la barre horizontale, placée à une hauteur $H$. Le centre de masse $M_{(t=0)}$ du hobbyhorseur a alors pour coordonnées $x_0 = 0$ et $y_0 = h$ et sa vitesse initiale est représentée par le vecteur vitesse $\vec{v_0}$ incliné d’un angle $\alpha$ par rapport à l’horizontale. L’obstacle est à une distance $x = D$ du point $O$. On suppose que la trajectoire du système s’effectue dans le plan $xOy$.

Durant le saut, l’action exercée par l’air sur le système est considérée comme négligeable. On modélise la situation du saut d’obstacle sur la figure 2.

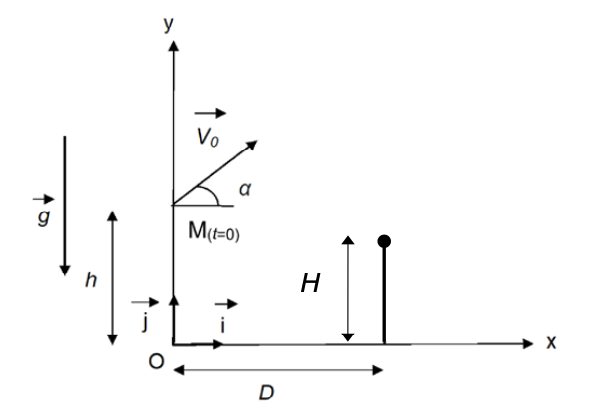
Figure 2. Représentation de la situation du saut d’obstacle, vu de profil et sans souci d’échelle.

Donnée :

• intensité du champ de pesanteur considéré uniforme : g = 9,81 m·s^–2.

Q7. En appliquant la deuxième loi de Newton dans le référentiel terrestre, déterminer les coordonnées ax(t) et ay(t) du vecteur accélération du centre de masse M du hobbyhorseur.

Système { hobbyhorseur }
Référentiel terrestre supposé galiléen

D’après la deuxième loi de Newton :
$$\sum \overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{P}=m\overrightarrow{a}$$
$$m\overrightarrow{g}=m\overrightarrow{a}$$
$$\overrightarrow{g}=\overrightarrow{a}$$

Or
$$\overrightarrow{g}\begin{pmatrix}0\\-g\end{pmatrix}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\overrightarrow{a}\begin{pmatrix}a_x(t)=0\\a_y(t)=-g\end{pmatrix}$$

Q8. Établir les équations horaires x(t) et y(t) décrivant le mouvement du centre de masse M du hobbyhorseur lors du saut.

$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$

On intègre :
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=C_1\\v_y(t)=-gt+C_2\end{pmatrix}$$

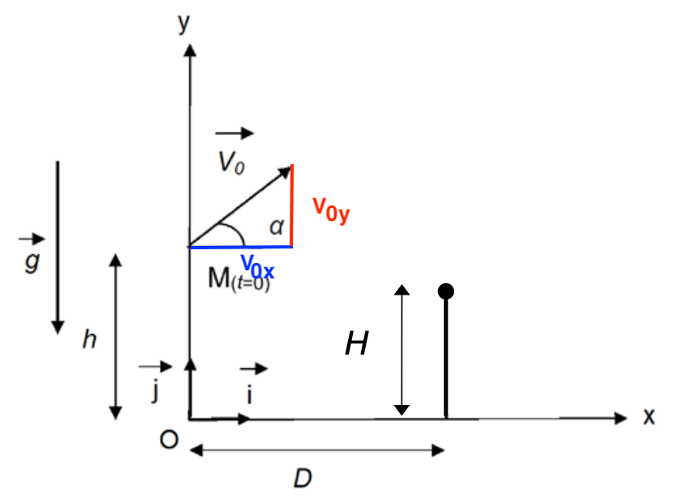
Donc :
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=v_0\cos\alpha\\v_y(t)=-gt+v_0\sin\alpha\end{pmatrix}$$

Puis :
$$\overrightarrow{OM}=\int \overrightarrow{v},dt$$
$$\overrightarrow{OM}\begin{pmatrix}x(t)=v_0\cos(\alpha)t+C_3\\y(t)=-\frac12 gt^2+v_0\sin(\alpha)t+C_4\end{pmatrix}$$

Avec $x_0=0$, $y_0=h$ :
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0\cos(\alpha)t\\y(t)=-\frac12 gt^2+v_0\sin(\alpha)t+h\end{pmatrix}$$

Q9. Montrer que l’équation de la trajectoire du centre de masse M du hobbyhorseur s’écrit sous la forme :

$$y(x) = -\frac{g}{2,v_0^2\cdot\cos^2(\alpha)}\cdot x^2 + \tan(\alpha)\cdot x + h.$$

$$x=v_0\cos(\alpha)t$$
$$t=\frac{x}{v_0\cos(\alpha)}$$

Alors :
$$y(x)=-\frac12 g\left(\frac{x}{v_0\cos(\alpha)}\right)^2+\tan(\alpha),x+h$$
$$y(x)=-\frac{g}{2v_0^2\cos^2(\alpha)}x^2+\tan(\alpha)x+h$$

Données :

• à l’instant initial, le hobbyhorseur se trouve au point M(t=0) tel  que OM_(t=0) = h = 1,19 m ;
• la distance D entre le point O et la base du support de la barre d’obstacle horizontale à franchir est D = 50,0 cm ;
• les jambes du hobbyhorseur sont repliées au maximum lors du saut et occupent un espace de 30 cm en-dessous de son centre de masse M ;

La trajectoire du centre de masse M du hobbyhorseur est modélisée par l’équation suivante, avec les coordonnées x et y exprimées en m :

y(x) = – 0,590 x² + 0,566 x + 1,19.

Q10. Déterminer si le hobbyhorseur franchira ou non la barre d’obstacle horizontale, placée à une hauteur H = 1,00 m du sol.

Pour la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée

Pour déterminer si le hobbyhorseur franchira ou non la barre d’obstacle horizontale, placée à une hauteur H = 1,00 m du sol, il faut calculer son altitude y pour la distance D entre le point O et la base du support de la barre d’obstacle horizontale à franchir x=D = 50,0 cm.

La trajectoire du centre de masse M du hobbyhorseur est modélisée par l’équation suivante, avec les coordonnées x et y exprimées en m :
$$y\left(x\right)=-0,590\ x^2+0,566\ x+1,19$$

$$y\left(x=D\right)=-0,590\ \left(50,0{\times10}^{-2}\right)^2+0,566\times50,0{\times10}^{-2}+1,19$$
$$y\left(x=D\right)=1,33\ m$$

Le centre de masse M est situé à une altitude de 1,32 m.
Or les jambes du hobbyhorseur sont repliées au maximum lors du saut et occupent un espace de 30 cm en-dessous de son centre de masse M.
$$1,33\ -30{\times10}^{-2}=1,03\ m$$

Les pieds du hobbyhorseur sont à une altitude de 1,03m, ainsi il franchira la barre d’obstacle horizontale, placée à une hauteur H = 1,00 m du sol.

Q11. À l’aide des données, calculer la valeur de l’angle α puis celle de la valeur de la vitesse initiale v₀ avec lesquelles le hobbyhorseur aborde l’obstacle. Indiquer comment le hobbyhorseur peut faire évoluer ces paramètres pour modifier sa trajectoire afin de sauter une barre d’obstacle de hauteur plus élevée.

D’après la question Q9. :
$$y\left(x\right)=-\frac{g}{2v_0^2\ \cos^2(\alpha)}x^2+\tan\left(\alpha\right)x+h$$

D’après les données :
$$y\left(x\right)=-0,590\ x^2+0,566\ x+1,19$$

Par identification :
$$\tan\left(\alpha\right)=0,566$$
$$\alpha=\tan^{-1}\left(0,566\right)$$
$$\alpha=29,5\ °$$

Par identification :
$$-\frac{g}{2v_0^2\ \cos^2(\alpha)}=-0,590$$
$$\frac{g}{2\ \cos^2(\alpha)}=0,590\times v_0^2$$
$$0,590\times v_0^2=\frac{g}{2\ \cos^2(\alpha)}$$
$$v_0^2=\frac{g}{0,590\times 2\ \cos^2(\alpha)}$$
$$v_0=\sqrt{\frac{g}{0,590\times 2\ \cos^2(\alpha)}}$$
$$v_0=\sqrt{\frac{9,81}{0,590\times 2\ \cos^2(29,5\ )}}$$
$$v_0=3,3\ m.s^{-1}$$

$$y\left(x\right)=-\frac{g}{2v_0^2\ \cos^2(\alpha)}x^2+\tan\left(\alpha\right)x+h$$

L’altitude dépends de l’inverse de la vitesse initiale au carré.
L’altitude dépends l’angle α, cependant sa dépendance est complexe car dépendant inversement de la fonction cos et également de la fonction tan.

Pour modifier sa trajectoire afin de sauter une barre d’obstacle de hauteur plus élevée, le hobbyhorseur peut :
• Augmenter la valeur de sa vitesse initiale.
• Trouver l’angle α le plus adapté.

Le hobbyhorseur réalise un deuxième saut. La figure 3 représente l’évolution de la vitesse initiale v₀ en fonction de la hauteur maximale y_max du centre de masse M du même hobbyhorseur avec un angle α’ par rapport au sol de 55°, une distance D de valeur égale à 50,0 cm ainsi qu’une hauteur initiale telle que OM_(t=0) = h = 1,19 m.

Le record du monde de saut d’obstacles en hobby horse a été établi à une hauteur d’obstacle de 1,40 m en 2019 par Marie Karkkainen lors du championnat du monde de la discipline en Finlande.

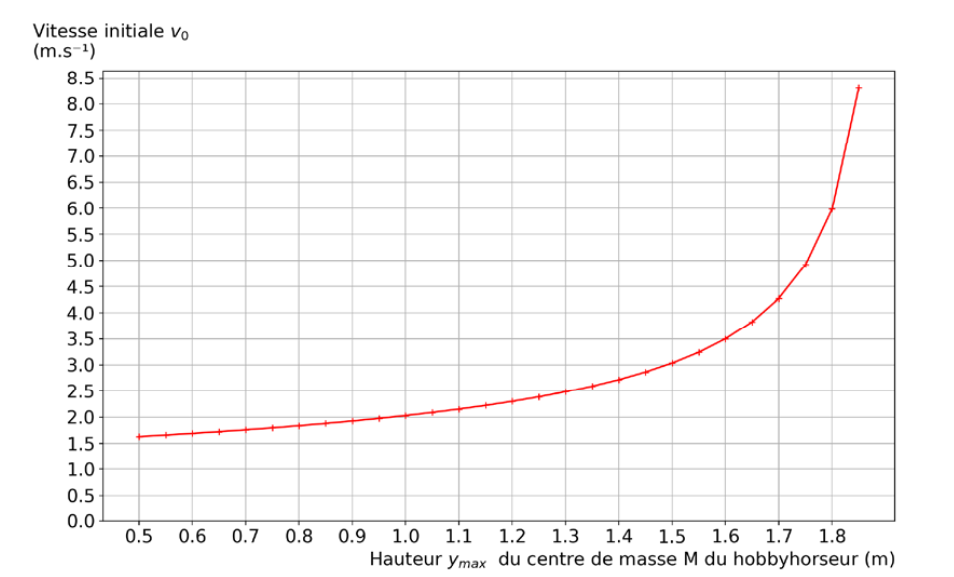
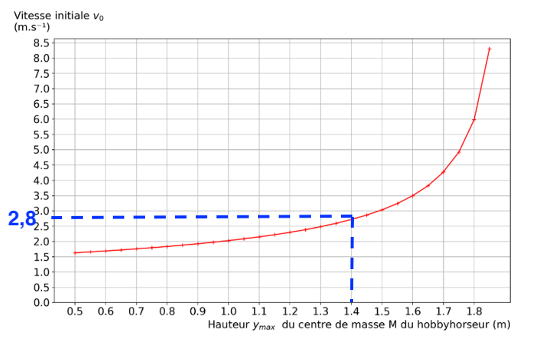
Figure 3. Représentation graphique de l’évolution de la vitesse initiale v₀ en fonction de la hauteur maximale y_max du centre de masse M du hobbyhorseur pour un angle α’ de valeur égale à 55°.

Q12. À partir de la figure 3, déterminer la valeur de la vitesse initiale v₀ avec laquelle le hobbyhorseur doit arriver sur l’obstacle pour espérer égaler le record mondial. Indiquer si cela est réalisable par ce hobbyhorseur sachant qu’habituellement lors des entraînements, sa vitesse initiale v₀ est comprise entre 11,5 et 13,5 km∙h^–1.

Habituellement lors des entraînements, sa vitesse initiale v₀ est comprise entre 11,5 et 13,5 km∙h^–1. Convertissons la vitesse trouvée en km∙h^–1
$$2,8\ m.s^{-1}=2,8\times 3,6=10\ km.h^{-1}$$

La vitesse nécessaire est inférieure à la vitesse initiale lors de ses entrainements. Ainsi, cela est réalisable par ce hobbyhorseur.