Bac Amérique du nord 2024 Sujet 2
Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°24-PYCJ2AN1
Sujet et corrigé
EXERCICE 2 : une batterie comestible (5 points)
L’électronique comestible est au cœur de l’attention des scientifiques qui cherchent à améliorer la réalisation de certains diagnostics de santé, et le déploiement d’équipements médicaux facilement ingérables et sans danger.
Un nouveau pas vient d’être franchi avec la création d’une batterie rechargeable entièrement comestible, pouvant se dissoudre dans le corps humain en toute sécurité.

Prototype de batterie comestible développée par les chercheurs de l’Institut Italien de Technologie
D’après https://www.futura-sciences.com/
Dans cet exercice, on s’intéresse à deux utilisations possibles de ce prototype :
- alimenter de petits équipements électroniques permettant de surveiller la santé d’un patient ;
- remplacer les piles rechargeables présentes dans les jouets, dispositifs sources d’intoxication après ingestion par les jeunes enfants.
1. Composition et fonctionnement de la pile
Le prototype réalisé par des chercheurs italiens est constitué de deux électrodes :
- la première notée CA / R est en or, recouverte de charbon actif et de 0,75 mg de riboflavine ou vitamine B2;
- la seconde notée CA / Q est en or, recouverte de charbon actif et de 0,60 mg de quercétine (pigment végétal présent dans les câpres ou l’oignon rouge).
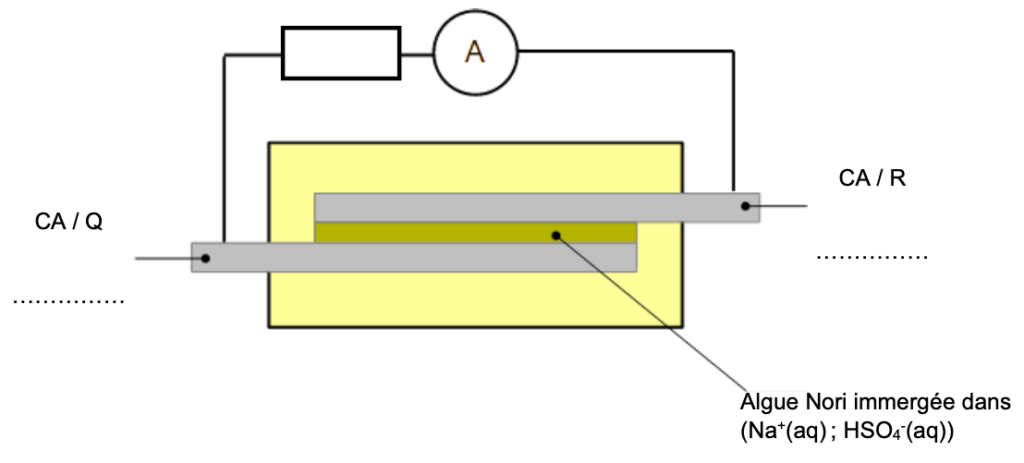
L’ensemble est séparé par un film d’algue Nori immergé dans une solution électrolytique d’hydrogénosulfate de sodium (Na+(aq) ; HSO4 –(aq)) puis encapsulé dans de la cire d’abeille (Figure 1).

Figure 1 : composition de la pile – D’après Adv. Mater. 2023, 35, 2211400
Lors de son fonctionnement, la pile permet d’obtenir une tension de 0,65 V et de délivrer un courant d’intensité constante de 48 μA pendant une durée Δt = 12 minutes. Ce courant permet selon les scientifiques italiens d’alimenter de petits dispositifs médicaux.
Données :
- informations relatives à la riboflavine et la quercétine :
| Formule Brute | Masse molaire moléculaire (g·mol-1) | Couple oxydant / réducteur | |
| riboflavine (R) | C17H20N4O6 | 376,36 | C17H18N4O6(s) / C17H20N4O6(s) |
| quercétine (Q) | C15H10O7 | 302,24 | C15H10O7(s) / C15H12O7(s) |
- nombre d’Avogadro : NA = 6,02×1023 mol-1 ;
- charge élémentaire e = 1,6×10-19 C ;
- constante de Faraday : F = 96 500 C·mol-1.
Le Faraday est la valeur absolue de la charge électrique d’1 mol d’électrons.
Q.1. Écrire l’équation de la réaction électrochimique modélisant la transformation de la riboflavine lors du fonctionnement de la pile.
La riboflavine de formule $C_{17}H_{20}N_4O_6$ appartient au couple $C_{17}H_{18}N_4O_6/C_{17}H_{20}N_4O_6$
L’équation de la réaction électrochimique modélisant la transformation de la riboflavine lors du fonctionnement de la pile s’écrit :
$$C_{17}H_{20}N_4O_6=C_{17}H_{18}N_4O_6+2H^++2e^-$$
Q.2. En déduire si la riboflavine subit une oxydation ou une réduction. Justifier.
La riboflavine cède des électrons, elle subit une oxydation.
La pile comestible est utilisée pour alimenter une résistance.
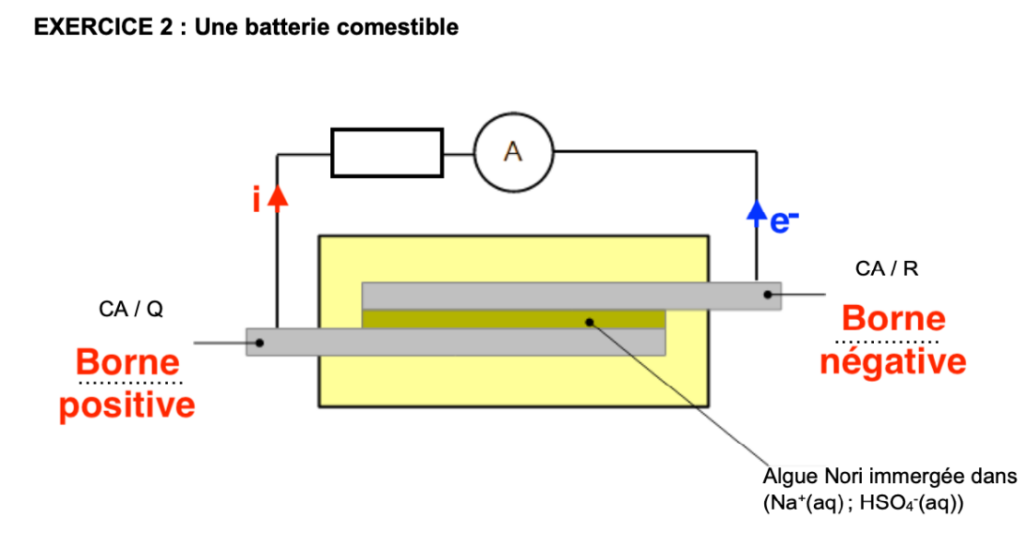
Q.3. Compléter le schéma de fonctionnement de la pile situé en ANNEXE à rendre avec la copie en mentionnant :
- la borne positive
- la borne négative
- le sens du courant dans le circuit
- le sens des électrons dans le circuit
La riboflavine (R) cède des électrons : c’est la borne négative
La quercétine (Q) reçoit des électrons : c’est la borne positive
Le sens du courant est de la borne positive vers la borne négative dans le circuit
Le sens des électrons est de la borne négative vers la borne positive dans le circuit
Q.4. Indiquer le rôle joué par le film d’algue Nori immergé dans la solution électrolytique d’hydrogénosulfate de sodium (Na+(aq) ; HSO4–(aq)).
La membrane joue le rôle d’un pont salin.
Elle assure l’électroneutralité des électrolytes des compartiments et permet de fermer le circuit.
La réaction électrochimique modélisant la transformation mise en jeu sur l’électrode recouverte de quercétine est :
C15H10O7(s) + 2 H+(aq) + 2 e– = C15H10O7(s)
Q.5. Déterminer la charge électrique Q délivrée par la pile pendant les 12 min de fonctionnement.
$$Q=I\times \Delta t$$
$$Q=48\times {10}^{-6}\times 12\times 60$$
$$Q=3,5\times {10}^{-2}\ C$$
Q.6. En déduire que la quantité de matière d’électrons ne consommée par l’électrode recouverte de quercétine pendant la durée Δt vaut ne = 3,6×10-7 mol.
$$Q=n_{e^-}\times N_a\times e$$
$$n_{e^-}\times N_a\times e=Q$$
$$n_{e^-}=\frac{3,5\times {10}^{-2}}{6,02\times {10}^{23}\times 1,6\times {10}^{-19}}$$
$$n_{e^-}=3,6\times {10}^{-7}\ mol$$
Q.7. Indiquer si, au bout de 12 min, la demi–pile est déchargée en calculant le pourcentage de quercétine qui a été consommée pendant cette durée.
$$n_{C_{15}H_{10}O_7\ consommé}=\frac{m_{C_{15}H_{10}O_7\ consommé}}{M_{C_{15}H_{10}O_7}}$$
$$\frac{m_{C_{15}H_{10}O_7\ consommé}}{M_{C_{15}H_{10}O_7}}=n_{C_{15}H_{10}O_7\ consommé}$$
$$m_{C_{15}H_{10}O_7\ consommé}=n_{C_{15}H_{10}O_7\ consommé}\times M_{C_{15}H_{10}O_7}$$
La réaction électrochimique modélisant la transformation mise en jeu sur l’électrode recouverte de quercétine est :
$$C_{15}H_{10}O_7+2H^++2e^-=C_{15}H_{12}O_7$$
Ainsi,
$$n_{C_{15}H_{10}O_7\ consommé}=\frac{n_{e^-}}{2}$$
Ainsi
$$m_{C_{15}H_{10}O_7\ consommé}=\frac{n_{e^-}}{2}\times M_{C_{15}H_{10}O_7}$$
$$m_{C_{15}H_{10}O_7\ consommé}=\frac{3,6\times 10^{-7}}{2}\times 302,24$$
$$m_{C_{15}H_{10}O_7\ consommé}=5,4\times 10^{-5}\ g$$
Calculons le pourcentage de quercétine qui a été consommée pendant cette durée :
$$P=\frac{m_{C_{15}H_{10}O_7\ consommé}}{m_{C_{15}H_{10}O_7\ initiale}}$$
$$P=\frac{5,4\times {10}^{-5}}{0,60\times {10}^{-3}}$$
$$P=0,09$$
$$P=9,0\ %$$
Le pourcentage de quercétine qui a été consommée pendant cette durée est de 9 %, il reste encore beaucoup de quercétine. Ainsi, au bout de 12 min, la pile n’est pas déchargée.
2. Recharge de la pile
Une deuxième possibilité d’application de cette batterie comestible est son utilisation pour remplacer les piles Lithium-Ion ou Nickel Métal Hybride utilisées dans les jouets. En effet, ces dernières présentent un danger d’intoxication en cas d’ingestion par un jeune enfant.
Les scientifiques italiens ont étudié le comportement de leur prototype après plusieurs charges
sous une tension comprise entre 0,60 et 0,80 V pour un courant de 48 μA (Figure 2).
Q.8. Indiquer la courbe qui représente la charge de la batterie comestible en analysant le graphe de la figure 2 Expliquer.
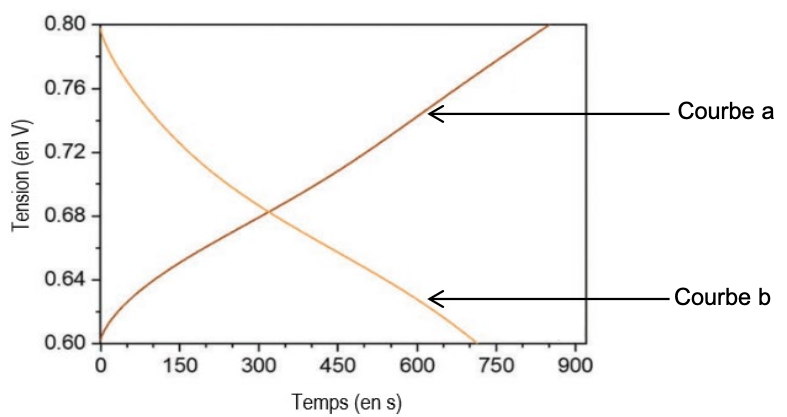
Figure 2 : charge et décharge de la batterie – D’après Adv. Mater. 2023, 35, 2211400
Lors de la charge de la batterie comestible, la tension à ses bornes augmente : courbe a.
On cherche à comparer la capacité d’une pile comestible à celle d’une pile classique Nickel Métal Hybride.
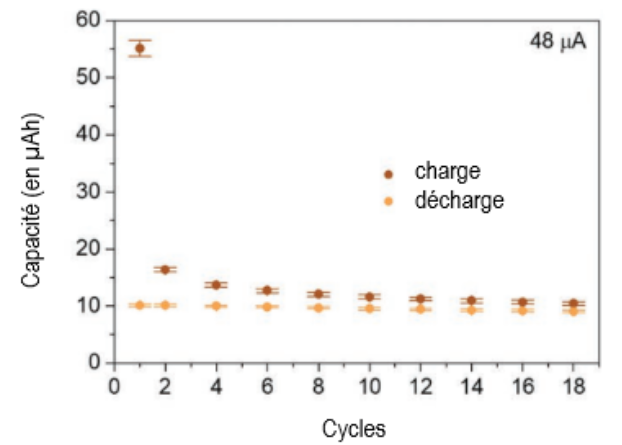
Figure 3 : capacité électrique de la batterie comestible après plusieurs cycles charge / décharge – D’après Adv. Mater. 2023, 35, 2211400

Figure 4 : pile Nickel Métal Hybride (NMH)– D’après Adv. Mater. 2023, 35, 2211400
Q.9. Calculer, avec les données fournies par la figure 4, la capacité en Ampèreheure (notée A·h) de la pile Nickel Métal Hybride. Discuter de la possibilité d’une réelle application de la batterie comestible dans la vie courante.
$$Q=I\times \Delta t$$
Or
$$P=U\times I$$
$$U\times I=P$$
$$I=\frac{P}{U}$$
D’ou
$$Q=\frac{P}{U}\times \Delta t$$
Or
$$P=E\Delta t$$
D’ou
$$Q=\frac{E}{U}$$
$$Q=0,04\ A.h$$
Comparons aux capacités des batteries comestibles :
$$\frac{Q}{Q_{comestible}}=\frac{0,04}{10\times {10}^{-6}}$$
$$\frac{Q}{Q_{comestible}}=4000$$
Les capacités des batteries comestibles sont 4000 fois plus faibles que celle des piles Nikel Métal Hybride utilisées.
Ainsi, on ne peut pas utiliser ces batteries comestibles dans la vie courante.
Annexe à rendre avec la copie
EXERCICE 2 : Une batterie comestible