Bac Métropole Septembre 2024 Sujet 1
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°24-PYCJ1ME3
Sujet et corrigé
Exercice 1 – L’acide citrique comme produit ménager (9 points)
L’acide citrique est un acide naturellement présent dans les fruits, en particulier dans le jus de citron. Ses propriétés acides en font un détartrant utilisé comme produit ménager.
Le but de cet exercice est de déterminer la quantité de matière d’acide citrique présente dans le jus extrait d’un citron puis de vérifier l’indication
« 1 pelle doseuse = la puissance de 10 citrons » notée sur l’emballage d’un produit ménager (voir photo ci-contre).

Données :
- l’acide citrique est un triacide, il est noté H3A dans cet exercice ;
- les autres espèces acide-base associées à l’acide citrique sont notées H2A–, HA2– et A3– ;
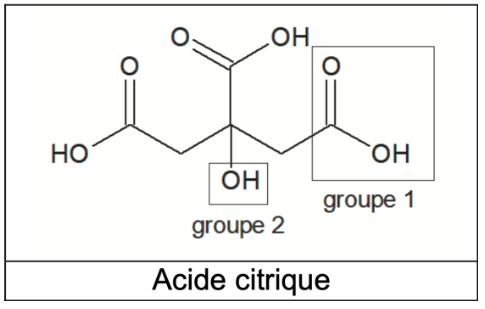
- formules topologiques :
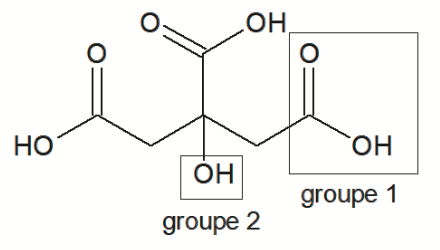
Acide citrique
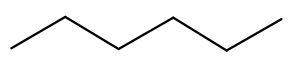
Hexane
- masse molaire de l’acide citrique : M = 192,1 g·mol–1 ;
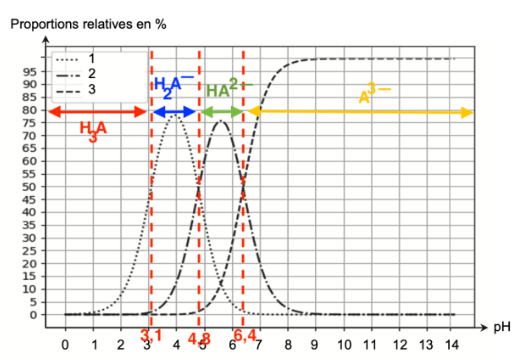
- pKA à 25 °C des couples acide/base associés à l’acide citrique : pKA1 = 3,1 ; pKA2 = 4,8 ; pKA3 = 6,4 ;
- concentration standard : c° = 1 mol·L–1 ;
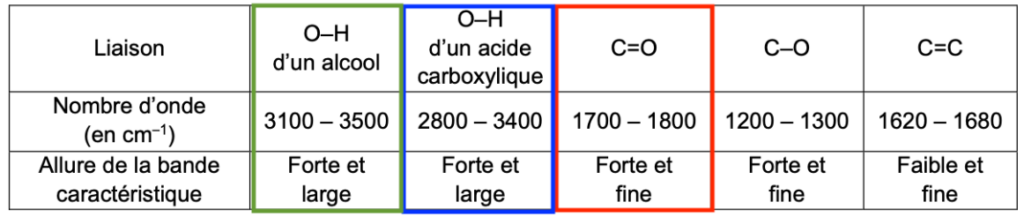
- données de spectroscopie infrarouge :
| Liaison | O–H d’un alcool | O–H d’un acide carboxylique | C=O | C–O | C=C |
| Nombre d’onde (en cm–1) | 3100 – 3500 | 2800 – 3400 | 1700 – 1800 | 1200 – 1300 | 1620 – 1680 |
| Allure de la bande caractéristique | Forte et large | Forte et large | Forte et fine | Forte et fine | Faible et fine |
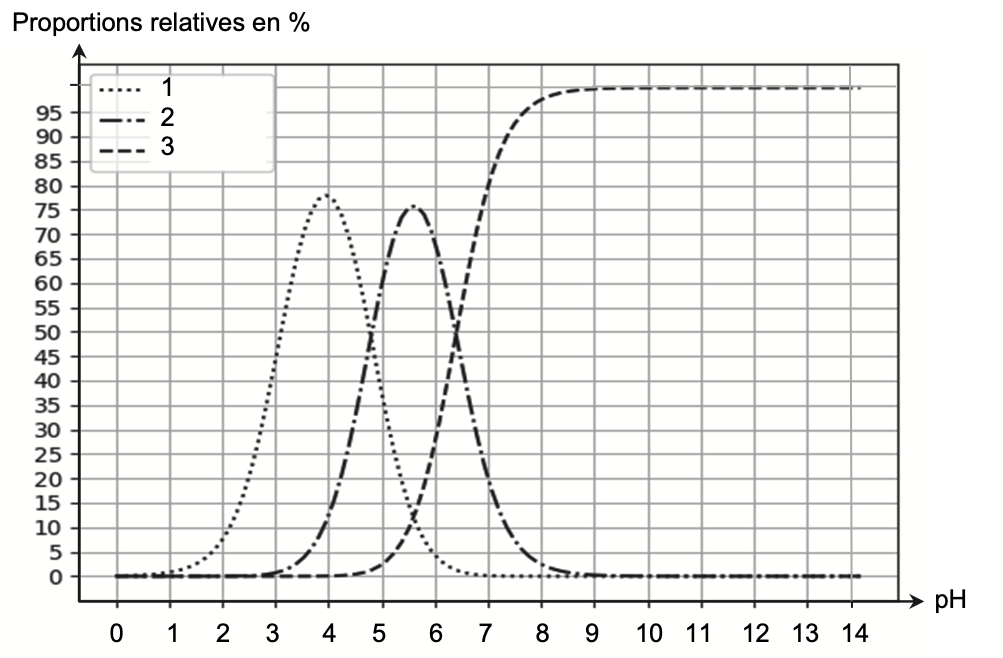
- diagramme de distribution de différentes espèces acido-basiques des couples associés à l’acide citrique :
1. Étude de quelques propriétés de l’acide citrique
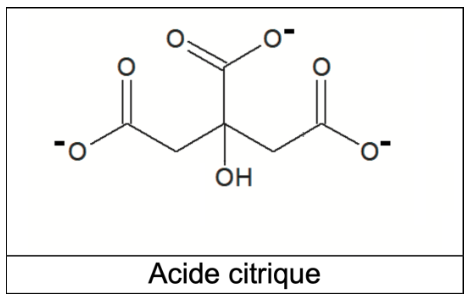
Q1. Nommer les groupes caractéristiques 1 et 2 encadrés sur la formule topologique de l’acide citrique. Préciser celui qui est responsable des propriétés acides de la molécule dans l’eau.
Groupe 1 : Carboxyle
Groupe 2 : hydroxyle
Le groupe carboxyle est responsable des propriétés acides de la molécule dans l’eau.
Q2. Justifier que le spectre infrarouge de la figure 1 est compatible avec la structure chimique de l’acide citrique.
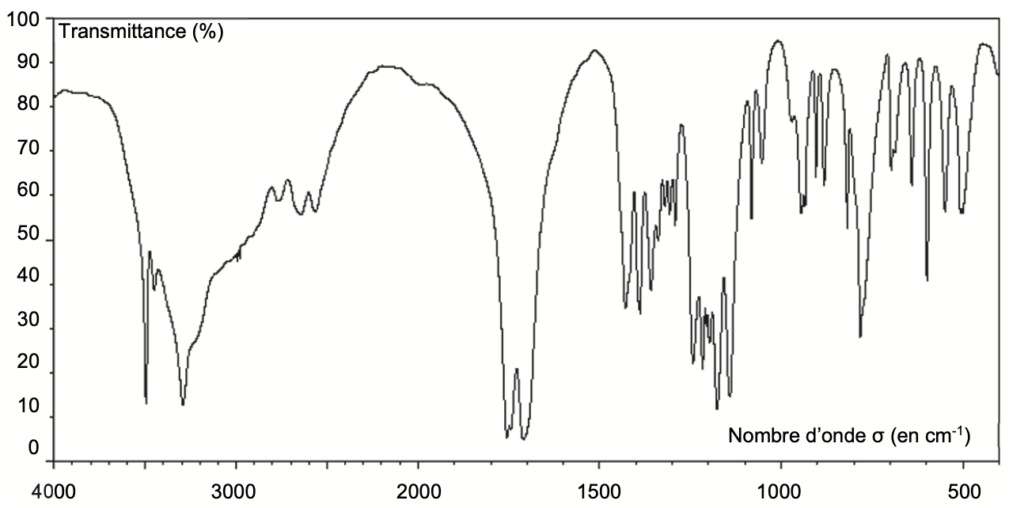
Figure 1. Spectre infrarouge de l’acide citrique
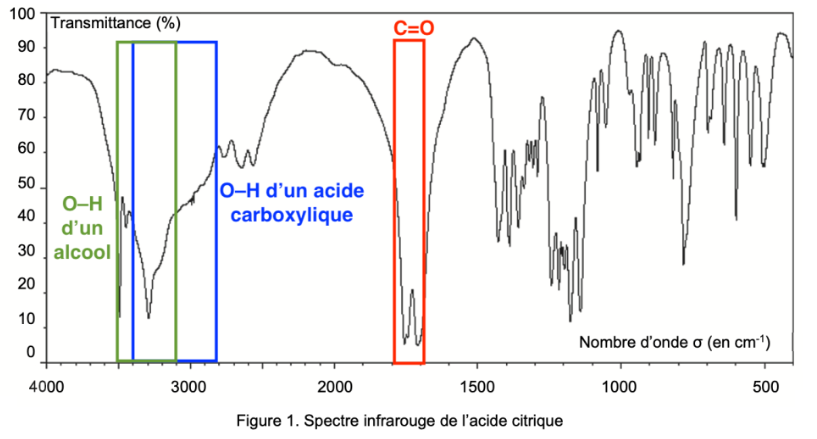
Le spectre présente :
une bande d’absorption entre 1700 -1800 cm-1 Forte et fine caractéristique d’une liaison C=O
une bande d’absorption autour de 2800 – 3400 cm-1 Forte et large caractéristique d’une liaison O-H d’un acide carboxylique.
une bande d’absorption autour de 3100 – 3500 cm-1 Forte et large caractéristique d’une liaison O-H d’un alcool. L’acide citrique possède, des liaisons C=O et O-H (acide carboxylique) ainsi qu’une liaison O-H d’un alcool.
Ainsi, le spectre infrarouge de la figure 1 est compatible avec la structure chimique de l’acide citrique.
La solubilité de l’acide citrique dans l’eau à 25 °C est égale à 592 g·L–1. La solubilité de l’hexane dans l’eau vaut 9,5 mg·L–1.
Q3. Proposer une explication de la différence entre ces deux valeurs de solubilité.
L’eau est un solvant polaire. L’acide citrique est polaire (présence d’atomes d’oxygènes très électronégatifs) et peut faire des liaisons hydrogènes avec les molécules d’eau. Ainsi, l’acide citrique est très soluble dans l’eau.
L’eau est un solvant polaire. L’hexane apolaire (présence d’atomes de carbone et d’hydrogènes uniquement) et ne peut donc pas faire des liaisons hydrogènes avec les molécules d’eau. Ainsi, l’hexane n’est pas soluble dans l’eau.
Q4. Attribuer à chaque courbe numérotée du diagramme de distribution de l’acide citrique l’espèce chimique correspondante. Justifier ces attributions.
Diagramme de prédominance :

Lorsque pH<3,1 : H3A est prédominant. L’espèce chimique H3A n’est pas représentée sur le diagramme de distribution.
Lorsque 3,1<pH<4,8 : H2A— est prédominant. Ainsi la courbe 1 correspond à l’espèce chimique H2A—.
Lorsque 4,8<pH<6,4 : HA2— est prédominant. Ainsi la courbe 2 correspond à l’espèce chimique HA2—.
Lorsque pH>6,4 : A3— est prédominant. Ainsi la courbe 3 correspond à l’espèce chimique A3—.
L’équation modélisant la réaction entre l’acide citrique H3A et l’eau est :
H3A(aq) + H2O(𝘗)→ H2A–(aq) + H3O+(aq)
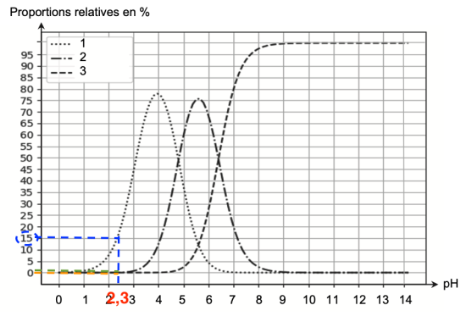
On dispose au laboratoire d’une solution aqueuse d’acide citrique de concentration c = 2,6×10–2 mol·L–1. Son pH vaut environ 2,3.
Q5. Estimer, à l’aide du diagramme de distribution, les proportions en pourcentage de chaque espèce acido- basiques H3A et H2A– de cette solution.
D’après le sujet, le pH de cette solution vaut environ 2,3.
Graphiquement, il y’a 15% de H2A—(courbe 1), 0% de HA2— (courbe 2) et 0% A3—(courbe 3).
Ainsi, il y a 100—15=85 % de H3A.
Q6. En déduire, par le calcul, qu’à pH = 2,3 les concentrations des espèces chimiques H3A et H2A– sont voisines de [H3A]éq = 2,2×10–2 mol·L–1 et [H2A–]éq = 3,9×10–3 mol·L–1.
D’après le sujet, la solution aqueuse d’acide citrique est de concentration c = 2,6×10–2 mol·L–1.
D’après la question précédente, il y’a 15% de H2A— et 85 % de H3A dans cette solution.
$\left[H_2A^-\right]=\frac{15}{100}\times c$
$\left[H_2A^-\right]=\frac{15}{100}\times 2,6\times {10}^{-2}$
$\left[H_2A^-\right]=3,9\times {10}^{-3}\ mol\cdot L^{-1}$
$\left[H_3A\right]=\frac{85}{100}\times c$
$\left[H_3A\right]=\frac{85}{100}\times 2,6\times {10}^{-2}$
$\left[H_3A\right]=2,2\times {10}^{-2}\ mol\cdot L^{-1}$
Q7. Donner l’expression de la constante d’acidité KA1 du couple H3A(aq)/H2A–(aq) en fonction des concentrations en quantité de matière à l’équilibre [H3A]éq, [H2A–]éq, [H3O+]éq et de la concentration standard c°.
En déduire l’égalité $\frac{[H_2A^-]{\text{eq}}}{[H_3A]{\text{eq}}}=10^{\text{pH}-\text{p}K_{A1}}$
KA1 du couple H3A(aq)/H2A–(aq) :
$K_{A1}=\frac{[H_2A^-]{eq}\times [H_3O^+]{eq}}{[H_3A]_{eq}\times c^0}$
$\frac{[H_2A^-]{eq}\times [H_3O^+]{eq}}{[H_3A]{eq}\times c^0}=K_{A1}$
Or
$\left[H_3O^+\right]=c^0\times {10}^{-pH}$
$\frac{[H_2A^-]{eq}\times c^0\times 10^{-pH}}{[H_3A]{eq}\times c^0}=K_{A1}$
$\frac{[H_2A^-]{eq}\times 10^{-pH}}{[H_3A]{eq}}=K_{A1}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=K_{A1} \times 10^{pH}$
Or
$K_{A1}={10}^{-pK_{A1}}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=10^{-pK_{A1}}10^{pH}$
Ainsi :
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=10^{pH-pK_{A1}}$
Q8. Déterminer si les proportions du diagramme de distribution à pH = 2 ,3 sont cohérentes avec la valeur du quotient $\frac{[H_2A^-]{\text{eq}}}{[H_3A]{\text{eq}}}$ calculée à l’aide de la relation démontrée la question Q7.
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=10^{pH-pK_{A1}}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=10^{2,3-3,1}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=0,16$
D’après les résultats de la question Q6 :
$\left[H_2A^-\right]=3,9\times {10}^{-3}\ mol\cdot L^{-1}$ et $\left[H_3A\right]=2,2\times {10}^{-2}\ mol\cdot L^{-1}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=\frac{3,9\times 10^{-3}}{2,2\times 10^{-2}}$
$\frac{[H_2A^-]{eq}}{[H_3A]{eq}}=0,18$
Les proportions du diagramme de distribution à pH = 2 ,3 sont cohérentes avec la valeur du quotient $\frac{[H_2A^-]{eq}}{[H_3A]{eq}}$ calculée à l’aide de la relation démontrée la question Q7. L’écart trouvé est due aux incertitudes liées à la lecture graphique peu précise.
2. Titrage de l’acide citrique
Dans cette partie, on cherche à déterminer expérimentalement la masse d’acide citrique présente dans un citron. Le protocole expérimental suivant est réalisé :
- presser un citron avec un presse-agrumes ;
- filtrer le jus obtenu. Le volume de jus mesuré vaut Vjus = 46 mL après filtration ;
- diluer 10 fois le jus de citron filtré ;
- prélever un volume Vdilué = 25,0 mL de jus de citron dilué et réaliser le titrage par une solution aqueuse d’hydroxyde de sodium de concentration cB = 2,5×10–1 mol·L–1, à l’aide d’un suivi pH-métrique.
Les valeurs des trois pKA de l’acide citrique étant proches, les trois acidités sont titrées simultanément. L’équation de la réaction support du titrage s’écrit :
H3A(aq) + 3 HO–(aq) → A3–(aq) + 3 H2O(𝘗)
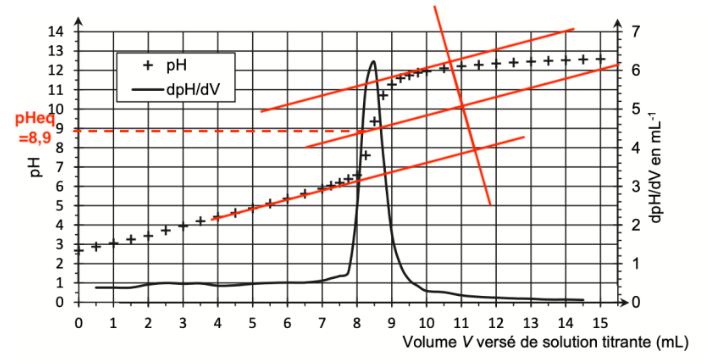
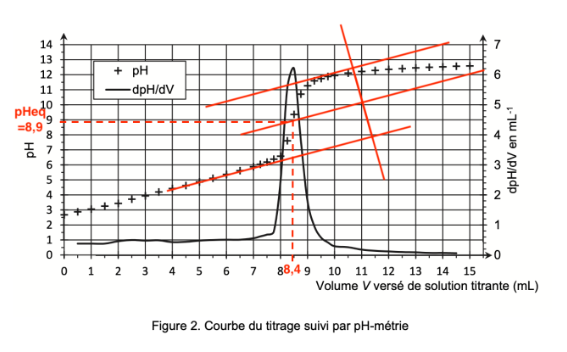
La courbe de titrage obtenue est représentée à la figure 2.
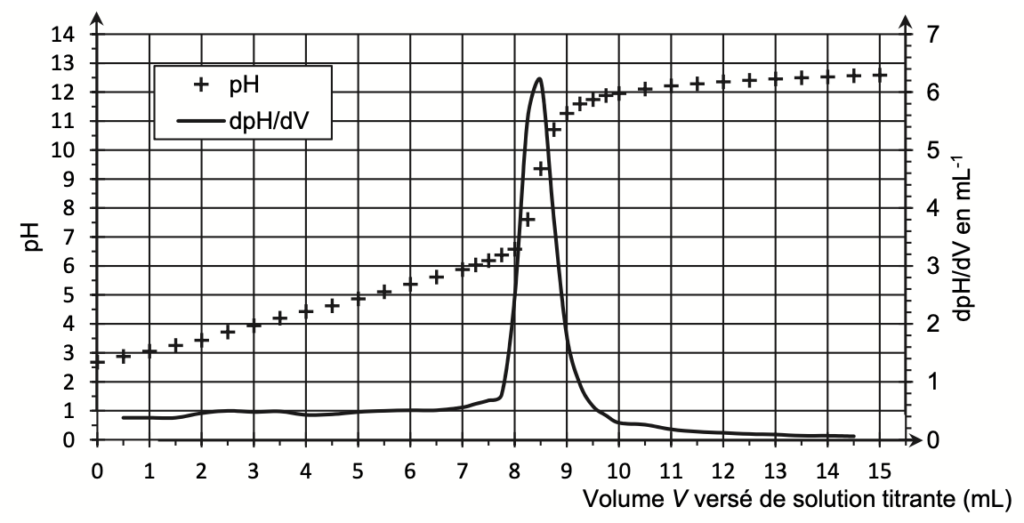
Figure 2. Courbe du titrage suivi par pH-métrie
Q9. À partir de la formule topologique de l’acide citrique H3A, représenter la formule semi-développée de l’ion A3–.
Formule topologique de l’acide citrique H3A :
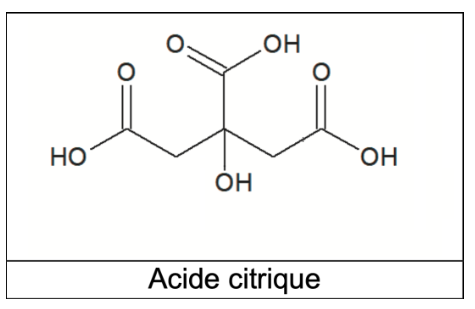
L’acide citrique possède 3 groupes caractéristique carboxyle (COOH). Chaque groupe carboxyle peut donner un ion H+.
Formule semi-développée de l’ion A3– :
Q10. Proposer un protocole expérimental permettant de diluer 10 fois le jus de citron filtré. Justifier la verrerie utilisée.
Protocole expérimental permettant de diluer 10 fois le jus de citron filtré.
On souhaite diluer 10 fois, ainsi le facteur de dilution est 10 : le volume de la solution fille est 10 fois plus grand que le volume de la solution mère.
Protocole expérimental :
- On prélève le volume Vm=10,0 mL à l’aide d’une pipete jaugée de 10,0 mL
- On introduit Vm=10,0 mL dans une fiole jaugée de volume Vf=100,0 mL
- On complète avec de l’eau distillée jusqu’au trait de jauge et on homogénéise.
Q11. Réaliser un schéma légendé du dispositif de titrage, en nommant le matériel et les solutions utilisées.
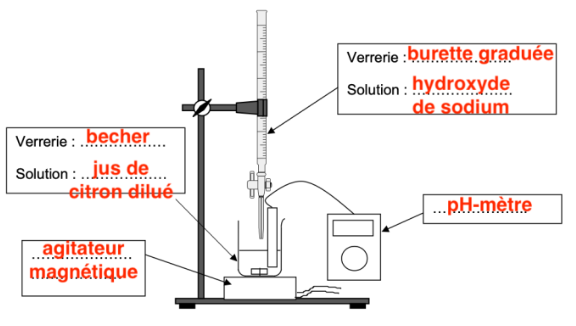
Q12. Choisir dans le tableau ci-dessous, en justifiant, un indicateur coloré adapté à ce titrage. Préciser, en justifiant, le changement de couleur de l’indicateur coloré à l’équivalence.
| Nom de l’indicateur coloré | Zone de virage | Teinte en milieu acide | Teinte en milieu basique |
| hélianthine | 3,1 – 4,4 | rouge | jaune |
| rouge de méthyle | 4,2 – 6,2 | rouge | jaune |
| bleu de bromothymol | 6,0 – 7,6 | jaune | bleu |
| phénolphtaléine | 8,2 – 10,0 | incolore | rose |
Un indicateur coloré est adapté au titrage si le pHeq est compris dans sa zone de virage.
En utilisant la méthode des tangentes parallèles, déterminons pHeq à l’aide de la Figure 2. pHeq=8,9.
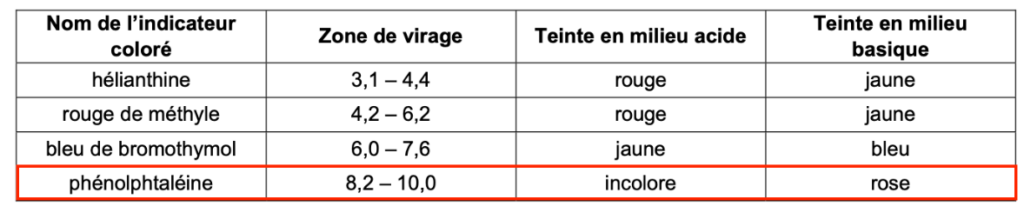
pHeq=8,9 est compris dans sa zone de virage de la phénolphtaléine. Ainsi, la phénolphtaléine est un indicateur coloré adapté à ce titrage.
La solution dosée est acide (acide citrique dilué de pH=2,7). Avant l’équivalence, la phénolphtaléine prend sa teinte acide qui est incolore.
Après l’équivalence, le pH est supérieur à 10, la phénolphtaléine prend sa teinte basique qui est rose.
Le changement de couleur de l’indicateur coloré à l’équivalence est d’incolore à rose.
Q13. En supposant que l’acide citrique est le seul acide présent dans le fruit, déterminer la masse d’acide citrique présente dans le citron.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
$H_3A_{(aq)}+3{\rm HO}{(aq)}^-\rightarrow A{(aq)}^{3-}+3H_2O_{(l)}$
A l’équivalence, les réactifs ont été introduits dans les proportions stœchiométrique :
$\frac{n_{H_3A}^i}{1}=\frac{n_{{\rm HO}^-}^{eq}}{3}$
$C_{A,diluee}\times V_{diluee}=\frac{C_B\times V_{eq}}{3}$
$C_{A,diluee}=\frac{C_B\times V_{eq}}{3\times V_{diluee}}$
On trouve graphiquement $V_{eq}$ :
$V_{eq}=8,4\ mL$
$C_{A,diluee}=\frac{2,5\times {10}^{-1}\times 8,4}{3\times 25,0}$
$C_{A,diluee}=2,8.{10}^{-2}\ mol.L^{-1}$
Or la solution est diluée 10 fois :
$C_A=10\times C_{A,diluee}$
$C_A=10\times 2,8.{10}^{-2}$
$C_A=2,8.{10}^{-1}\ mol.L^{-1}$
Déterminons la masse d’acide citrique présente dans le citron.
$n_{H_3A}=\frac{m_{H_3A}}{M_{H_3A}}$
$\frac{m_{H_3A}}{M_{H_3A}}=n_{H_3A}$
Or
$C_A=\frac{n_{H_3A}}{V_{jus\ de\ citron}}$
$\frac{n_{H_3A}}{V_{jus\ de\ citron}}=C_A$
$n_{H_3A}=C_A\times V_{jus\ de\ citron}$
D’où
$m_{H_3A}=C_A\times V_{jus\ de\ citron}\times M_{H_3A}$
$m_{H_3A}=2,8.{10}^{-1}\times 46\times {10}^{-3}\times 192,1$
$m_{H_3A}=2,5\ g$
Avec un protocole similaire, on détermine que la masse d’acide citrique contenue dans une pelle-doseuse est égale à 23 g.
Q14. En déduire le nombre de citrons apportant la même masse d’acide citrique. Commenter.
| 1 citron | 2,5 g |
| N citrons | 23 g |
$N=\frac{23\times 1}{2,5}$
$N=9,2$
9,2 de citrons apportent la même masse d’acide citrique contenue dans une pelle-doseuse.
Sur l’emballage est noté : « 1 pelle doseuse = la puissance de 10 citrons ».
L’indication de l’emballage est vérifiée.
