Bac Liban 2024 Sujet 2
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°24-PYCJ2G11
Sujet et corrigé
EXERCICE 1 : l’ammoniac : un futur carburant pour les transports maritimes (9 points)
L’industrie chimique produit chaque année 180 millions de tonnes d’ammoniac. L’ammoniac est principalement utilisé dans la production d’engrais et dans le stockage de l’énergie. C’est aussi un carburant potentiel pour les années futures, notamment dans le domaine des transports maritimes.
Dans les conditions normales de température et de pression, l’ammoniac, de formule NH3, est un gaz incolore à l’odeur très désagréable.
D’après le site Médiachimie.
Cet exercice comporte deux parties : la première s’intéresse à la molécule d’ammoniac et ses propriétés chimiques, la seconde traite de la synthèse de l’ammoniac et de l’amélioration du procédé.
1. Étude de la molécule et de ses propriétés chimiques
Données :
- numéro atomique de l’azote : Z(N) = 7 ;
- électronégativités : χ(N) = 3,04 ; χ(H) = 2,20 ; χ(O) = 3,44 ;
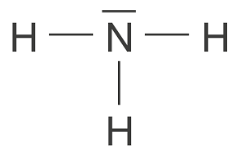
- la géométrie de la molécule d’ammoniac est pyramidale :
- pKA du couple NH4+ (aq) / NH3 (aq) = 9,2 ;
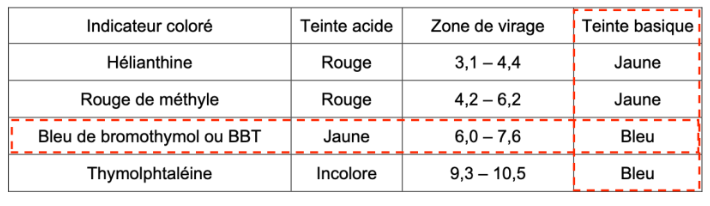
- zones de virage de quelques indicateurs colorés :
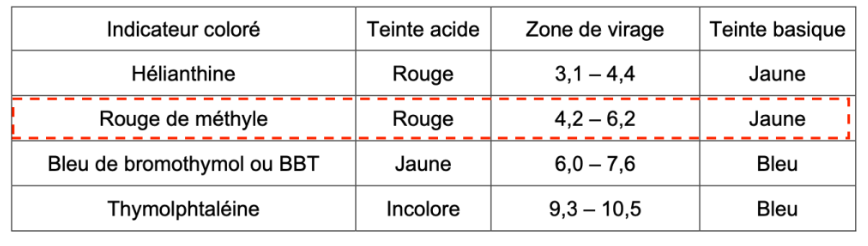
| Indicateur coloré | Teinte acide | Zone de virage | Teinte basique |
| Hélianthine | Rouge | 3,1 – 4,4 | Jaune |
| Rouge de méthyle | Rouge | 4,2 – 6,2 | Jaune |
| Bleu de bromothymol ou BBT | Jaune | 6,0 – 7,6 | Bleu |
| Thymolphtaléine | Incolore | 9,3 – 10,5 | Bleu |
Q.1. Représenter le schéma de Lewis de la molécule d’ammoniac.
Q.2. Donner un argument justifiant la grande solubilité de l’ammoniac dans l’eau.
$\Delta\chi=\chi N-\chi(H)$
$\Delta\chi=3,04-2,20$
$\Delta\chi=0,84$
La différence d’électronégativité entre l’azote et l’hydrogène est supérieure à 0,4 : les liaisons sont polarisées.
L’eau est un solvant polaire. Le caractère polaire de la molécule d’ammoniac peut expliquer la grande solubilité de l’ammoniac dans l’eau.
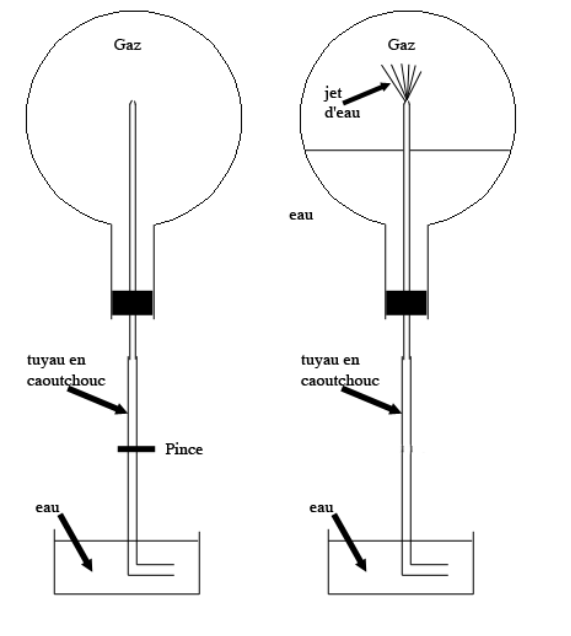
Pour vérifier la dissolution de l’ammoniac dans l’eau, on réalise l’expérience dite du jet d’eau.
Sous la hotte, on remplit de gaz ammoniac un ballon bien sec.
On immerge le tuyau de caoutchouc dans un cristallisoir contenant de l’eau à pH = 7. On observe alors un jet d’eau dans le ballon. Une fois le ballon totalement rempli de solution, on y ajoute du BBT.
Q.3. Définir une base selon Brönsted.
Selon Bronsted : Une base est une espèce chimique capable de capter un ou plusieurs proton(s) H+.
Q.4. Écrire l’équation de la réaction modélisant la transformation de l’ammoniac avec l’eau.
$NH_3\left(aq\right)+H_2O\left(l\right)\rightleftarrows NH_4^+aq+HO-aq$
Q.5. En déduire, en la justifiant, la couleur de la solution obtenue.
L’ion HO– apparait, la solution devient basique. Le BBT prend sa teinte basique : la solution devient bleue.
On mesure le pH de la solution aqueuse d’ammoniac obtenue : pH = 11,0.
Q.6. Indiquer l’espèce qui prédomine en justifiant la réponse à l’aide d’un diagramme de prédominance.
Diagramme de prédominance :

Pour pH=11, l’ammoniac NH3 est prédominant.
On simule le titrage d’un volume VB = 20,0 mL d’une solution aqueuse d’ammoniac de pH = 11,0 par de l’acide chlorhydrique (H3O+(aq) ; Cl– (aq)) de concentration CA = 0,100 mol·L-1.
On obtient la courbe suivante :
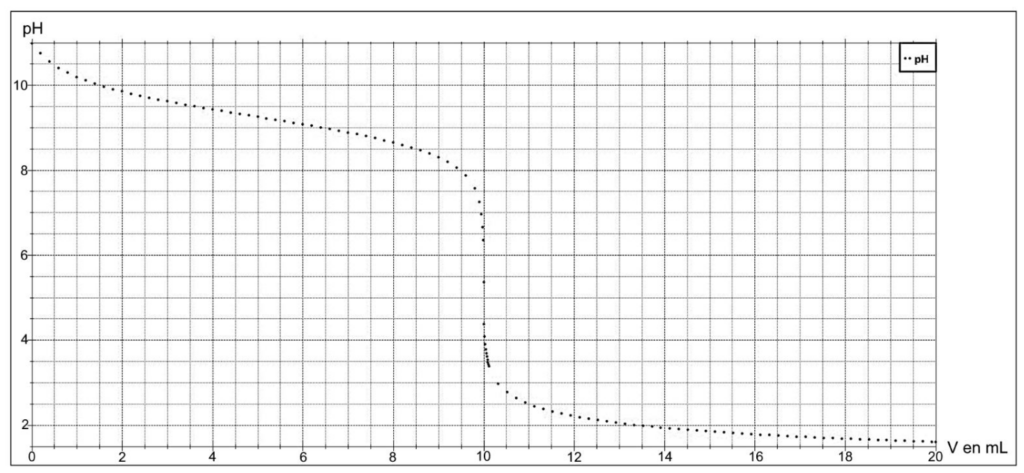
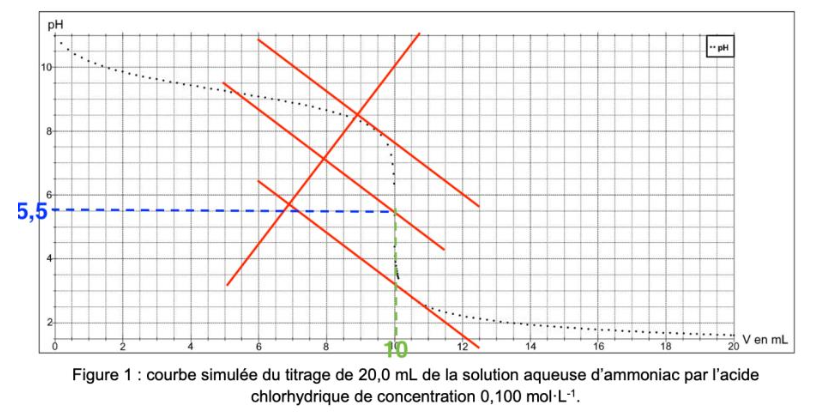
Figure 1 : courbe simulée du titrage de 20,0 mL de la solution aqueuse d’ammoniac par l’acide chlorhydrique de concentration 0,100 mol·L-1.
Q.7. Écrire l’équation de la réaction support du titrage.
$NH_3\left(aq\right)+H_3O^+\left(aq\right)\rightarrow NH_4^+\left(aq\right)+H_2O\left(l\right)$
Q.8. Justifier l’utilisation du rouge de méthyle comme indicateur coloré pour ce titrage.
pHeq=5,5
Pour choisir un indicateur coloré, il faut que le pHeq soit dans sa zone de virage.
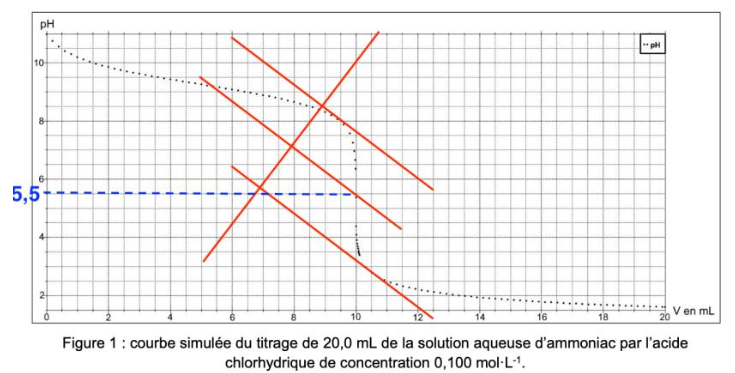
Le rouge de méthyle contient pHeq dans sa zone de virage. Ainsi, le rouge de méthyle convient comme indicateur coloré pour ce titrage.
Q.9. Déterminer la valeur de la concentration CB de la solution aqueuse d’ammoniac choisie pour cette simulation.
$NH_3\left(aq\right)+H_3O^+\left(aq\right)\rightarrow NH_4^+\left(aq\right)+H_2O\left(l\right)$
A l’équivalence, les réactifs sont introduits dans les proportions stœchiométriques :
$\frac{n_i\left(NH_3\right)}{1}=\frac{n_{eq}\left(H_3O^+\right)}{1}$
$n_i\left(NH_3\right)=n_{eq}\left(H_3O^+\right)$
$C_B\times V_B=C_A\times V_e$
$C_B=\frac{C_A\times V_e}{V_B}$
$C_B=\frac{0,100\times 10,0}{20,0}$
$C_B=5,0\times {10}^{-2}\ mol.L^{-1}$
2. Synthèse de l’ammoniac
En 1909, le chimiste allemand, Fritz Haber, chercheur à l’Université de Karlsruhe, réussit, en laboratoire, la synthèse de l’ammoniac NH3(g) à partir du diazote de l’air N2(g) et de dihydrogène H2(g).
Aujourd’hui, cette synthèse se fait sous une pression d’environ 300 bar, à 500 °C en présence d’un catalyseur riche en fer. En utilisant 6,0 mol de diazote et 6,0 mol de dihydrogène, on obtient 0,80 mol d’ammoniac.
Q.10. Écrire l’équation de la réaction modélisant la synthèse de l’ammoniac.
La synthèse (Produit) de l’ammoniac NH3(g) à partir (Réactifs) du diazote de l’air N2(g) et de dihydrogène H2(g)
$N_2\left(g\right)+3H_2\left(g\right)\rightarrow 2NH_3\left(g\right)$
Q.11. Déterminer l’avancement final xf de cette réaction dans les conditions données. Comparer la valeur obtenue à celle de l’avancement maximal et conclure.
| $N_2\left(g\right)$ | $+3H_2\left(g\right)$ | $\rightarrow 2NH_3\left(g\right)$ | |
| État initial | 6,0 | 6,0 | 0 |
| État intermédiaire | 6,0-x | 6,0-3x | 2x |
| État final | $6,0-x_f$ | $6,0-3x_f$ | $2x_f=0,80$ |
Calculons l’avancement final :
$2x_f=0,80$
$x_f=\frac{0,80}{2}$
$x_f=0,40\ mol$
Calculons l’avancement maximale :
$6,0-x_{max1}=0$
$-x_{max1}=-6,0$
$x_{max1}=6,0\ mol$
$6,0-3x_{max2}=0$
$-3x_{max2}=-6,0$
$x_{max2}=\frac{-6,0}{-3}$
$x_{max2}=2,0\ mol$
$x_{max2}<x_{max1}$ : $x_{max}=x_{max2}=2,0\ mol$
Comparons l’avancement final et l’avancement maximal :
$x_f<x_{max}$ : la réaction est limitée.
La société française ENGIE investit dans le développement d’un des premiers projets de dihydrogène renouvelable. Ce projet est situé dans la région de Pilbara en Australie. En 2024, la première phase produira 640 tonnes de dihydrogène par an. Le dihydrogène sera utilisé comme matière première pour la production d’ammoniac. Le rendement de la production d’ammoniac sera de 20 %.
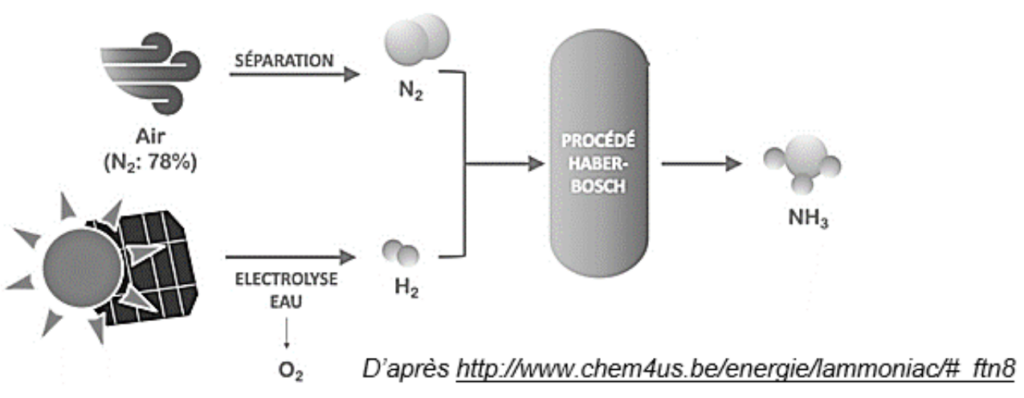
Figure 2 : schéma du procédé Haber-Bosch
Données :
- équations des réactions électrochimiques modélisant les transformations aux électrodes :
- 2 H+(aq) + 2 e– → H2(g)
- 2 H2O(l) → O2(g) + 4 H+(aq) + 4 e– ;
- volume molaire dans les conditions de l’expérience : Vm = 24 L·mol-1 ;
- nombre d’Avogadro : NA = 6,02×1023 mol-1 ;
- charge élémentaire e = 1,6×10-19 C ;
- quantité d’électricité Q : Q = I×Δt = ne-×NA×e avec ne- la quantité de matière d’électrons échangés (en mol) ;
- masses molaires atomiques en g·mol-1 : M(H) = 1,0 ; M(N) = 14,0.
L’électrolyse de l’eau utilisée dans l’usine de Pilbara peut être reproduite au laboratoire grâce au montage de la figure 3, en remplaçant la cellule photovoltaïque par un générateur.

Figure 3 : montage expérimental
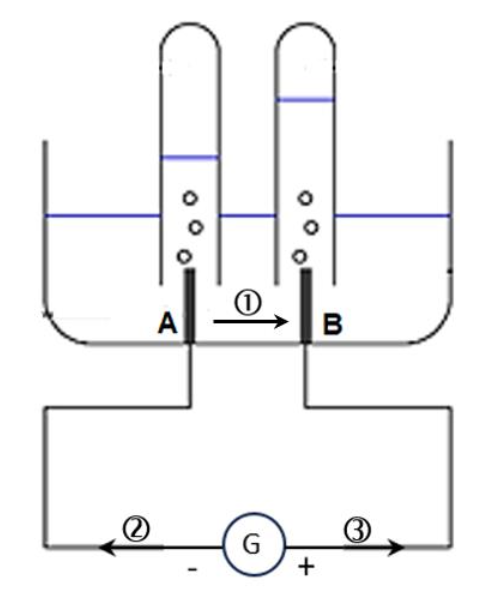
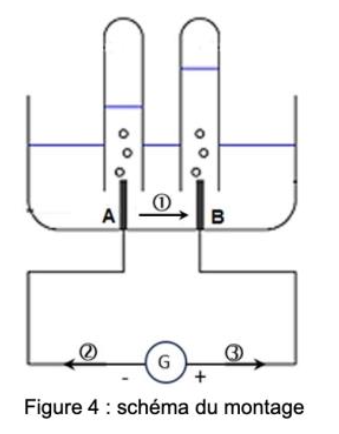
Figure 4 : schéma du montage
Q.12. Indiquer, parmi celles numérotées ①,② ou ③ sur la figure 4, les deux flèches représentant respectivement le sens du courant électrique et celui du déplacement des électrons.
1 :
2 : déplacement des électrons
3 : courant électrique
Q.13. Associer à chacune des électrodes, A et B, une des équations des réactions électrochimiques figurant dans les données et nommer les gaz formés à chaque électrode.
Les électrons arrivent sur l’électrode A. Les électrons sont consommés à cette électrode :
$2H^+\left(aq\right)+2e^-\rightarrow H_2\left(g\right)$
Le gaz formé sur l’électrode A est le dihydrogène H2. Sur l’électrode B les électrons sont produits :
$2H_2O\left(l\right)\rightarrow O_2\left(g\right)+4H^+\left(aq\right)+4e^-$
Le gaz formé sur l’électrode B est le dioxygène O2.
On recueille 4,0 mL de gaz dans un des tubes et 2,0 mL dans l’autre.
Q.14. Écrire l’équation de la réaction modélisant la transformation chimique qui se déroule dans l’électrolyseur. Valider la stœchiométrie des deux gaz formés en analysant les volumes de gaz obtenus aux électrodes.
$2\times\ \ \ \ \ \ 2H^+\left(aq\right)+2e^-\rightarrow H_2\left(g\right)$
$2H_2O\left(l\right)\rightarrow O_2\left(g\right)+4H^+\left(aq\right)+4e^-$
$4H^+\left(aq\right)+2H_2O\left(l\right)\rightarrow O_2\left(g\right)+4H^+\left(aq\right)+2H_2\left(g\right)$
$2H_2O\left(l\right)\rightarrow O_2\left(g\right)+2H_2\left(g\right)$
$\frac{n\left(O_2\right)}{1}=\frac{n\left(H_2\right)}{2}$
Or
$n=\frac{V}{V_m}$
$\frac{V\left(O_2\right)}{V_m}=\frac{\frac{V\left(H_2\right)}{V_m}}{2}$
$\frac{V\left(O_2\right)}{V_m}=\frac{V\left(H_2\right)}{2\times V_m}$
$V\left(O_2\right)=\frac{V\left(H_2\right)}{2}$
Ou
$V\left(H_2\right)=2\times V\left(O_2\right)\ $
On remarque que le volume de gaz formé (dihydrogène H2) à l’électrode A est deux fois supérieur au volume de gaz formé (dioxygène O2) à l’électrode B.
La manipulation dure Δt = 3 min et 20 s. L’intensité du courant est de 0,16 A.
Q.15. Calculer la quantité d’électricité Q ayant circulé dans le circuit électrique pendant la durée de l’électrolyse au laboratoire et en déduire la quantité de matière d’électrons échangés.
Calculons la quantité d’électricité Q :
$Q=I\times \Delta t$
$Q=0,16\times\left(3\times 60+20\right)\ $
$Q=32\ C$
Calculons la quantité́ de matière d’électrons échanges :
$Q=n\left(e^-\right)\times Na\times e$
$n\left(e^-\right)\times Na\times e=Q$
$n\left(e^-\right)=\frac{Q}{Na\times e}$
$n\left(e^-\right)=\frac{32}{6,02\times {10}^{23}\times 1,6\times {10}^{-19}}$
$n\left(e^-\right)=3,3\ \times {10}^{-4}\ mol$
Q.16. En déduire le volume de dihydrogène que l’on pourrait obtenir dans les conditions de l’expérience. Comparer aux données expérimentales.
$2H^+\left(aq\right)+2e^-\rightarrow H_2\left(g\right)$
$\frac{n\left(e^-\right)}{2}=\frac{n\left(H_2\right)}{1}$
$n\left(H_2\right)=\frac{n\left(e^-\right)}{2}$
Or
$n\left(H_2\right)=\frac{V\left(H_2\right)}{V_m}$
D’où
$\frac{V\left(H_2\right)}{V_m}=\frac{n\left(e^-\right)}{2}$
$V\left(H_2\right)=\frac{n\left(e^-\right)}{2}\times V_m$
$V\left(H_2\right)=\frac{3,3\ \times {10}^{-4}}{2}\times 24$
$V\left(H_2\right)=4,0\ \times {10}^{-3}\ L$
$V\left(H_2\right)=4,0\ mL$
Le volume trouvé est cohérent avec les données expérimentales (4,0 mL)
Q.17. Déterminer la masse d’ammoniac qui pourra être produite en 2024 à partir du dihydrogène produit dans l’usine de Pilbara. Commenter.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
D’après l’énoncé : « En 2024, la première phase produira 640 tonnes de dihydrogène par an ».
Calculons la masse d’ammoniac qui pourra être produite en 2024 à partir du dihydrogène produit dans l’usine de Pilbara en considérant la réaction totale :
$N_2\left(g\right)+3H_2\left(g\right)\rightarrow 2NH_3\left(g\right)$
$\frac{n\left(NH_3\right)}{2}=\frac{n\left(H_2\right)}{3}$
$n\left(NH_3\right)=2\times\frac{n\left(H_2\right)}{3}$
Or
$n=\frac{m}{M}$
$\frac{m\left(NH_3\right)}{M\left(NH_3\right)}=2\times\frac{m\left(H_2\right)}{3\times M\left(H_2\right)}$
$m\left(NH_3\right)=2\times\frac{m\left(H_2\right)}{3\times M\left(H_2\right)}\times M\left(NH_3\right)$
$m\left(NH_3\right)=2\times\frac{640\times {10}^3}{3\times\left(2\times 1,0\right)}\times\left(14,0+3\times 1,0\right)$
$m\left(NH_3\right)=3,6\times {10}^6\ kg$
$m\left(NH_3\right)=3,6\times {10}^3\ tonnes$
En considérant que le rendement de la production d’ammoniac sera de 20 %.
$m_{reel}\left(NH_3\right)=\frac{20}{100}\times m\left(NH_3\right)$
$m_{reel}\left(NH_3\right)=\frac{20}{100}\times 3,6\times {10}^{-3}$
$m_{reel}\left(NH_3\right)=720\ tonnes$
