Une série d’expériences historiques : la réaction d’estérification étudiée par Marcellin Berthelot

Bac Polynésie septembre 2024 Sujet 2

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°24-PYCJ2PO3

EXERCICE 1 – UNE SÉRIE D’EXPÉRIENCES HISTORIQUES : LA RÉACTION D’ESTÉRIFICATION ÉTUDIÉE PAR MARCELLIN BERTHELOT (9 POINTS)

Marcellin Berthelot (1827-1907), auteur de nombreuses découvertes en chimie, est considéré comme l’un des plus grands scientifiques français du dix-neuvième siècle. Avec l’aide de son élève, Léon Péan de Saint-Gilles, il a étudié de manière approfondie la réaction entre un alcool et un acide carboxylique.

L’objectif de cet exercice est de montrer comment la technique du dosage par titrage a permis à Marcellin Berthelot de mettre en évidence les notions de cinétique chimique et d’équilibre chimique.

1.   Dosage par titrage.

Berthelot et Péan de Saint-Gilles ont réalisé un mélange contenant les mêmes quantités de matière en acide éthanoïque et en éthanol laissé à la température ambiante de 20 °C. Il s’est formé de l’éthanoate d’éthyle et de l’eau. La transformation d’estérification qui s’est déroulée était très lente. Elle peut être modélisée par l’équation de réaction suivante :

CH₃COOH(ℓ) + C₂H₅OH(ℓ) ⇄ CH₃COOC₂H₅(ℓ) + H₂O(ℓ)

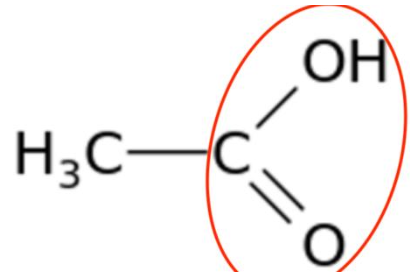
Q1. Représenter la formule semi-développée de l’acide éthanoïque. Entourer et nommer le groupe caractéristique de la molécule. Nommer la famille fonctionnelle à laquelle appartient l’éthanoate d’éthyle.

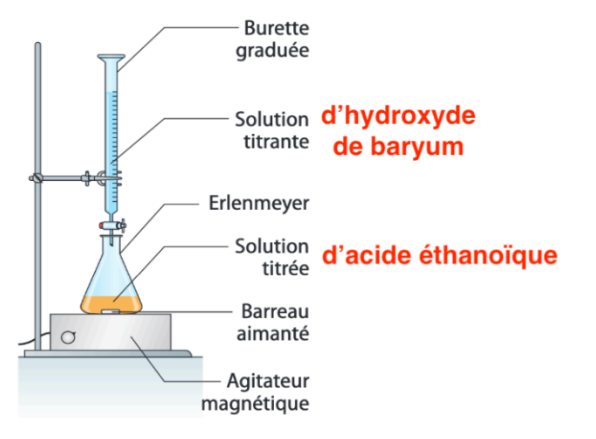
La transformation s’étant poursuivie pendant quinze jours, un échantillon du mélange réactionnel a alors été prélevé afin de connaître l’évolution des quantités de matière des espèces chimiques en jeu. Pour Marcellin Berthelot : « C’est évidemment l’acide qu’il faut déterminer. On transvase (l’échantillon) dans un vase à fond plat. On ajoute quelques gouttes de teinture de tournesol et l’on verse de l’eau de baryte avec une burette graduée jusqu’à ce que la teinte rose du tournesol ait viré au bleu franc. »

Données :

• Le vase à fond plat est un erlenmeyer ;
• La teinture de tournesol est un indicateur coloré acido-basique ;
• L’eau de baryte est une solution aqueuse d’hydroxyde de baryum : elle contient les ions baryum Ba²⁺(aq), spectateurs, et les ions hydroxyde HO⁻(aq) ;
• Couples acide / base mis en jeu : CH₃CO₂H(ℓ) / CH₃CO₂⁻(aq) ; H₂O(ℓ) / HO⁻(aq).

Q2. Faire un schéma du dosage par titrage réalisé en y indiquant les positions de la solution titrante et de la solution titrée.

Q3. Écrire l’équation de réaction qui modélise la transformation lors du dosage par titrage entre l’acide éthanoïque présent dans l’échantillon et les ions hydroxyde provenant de la burette. Citer au moins une caractéristique que doit posséder toute réaction utilisée pour un dosage par titrage.

Équation de réaction qui modélise la transformation lors du dosage par titrage entre l’acide éthanoïque présent dans l’échantillon et les ions hydroxyde provenant de la burette :
$${\rm CH}_3CO_2H\left(l\right)+{\rm HO}^-\left(aq\right)\longrightarrow{\rm CH}_3CO_2^-\left(aq\right)+H_2O(l)$$
Caractéristiques que doit posséder toute réaction utilisée pour un dosage par titrage :
Rapide
Totale
Unique
(Une seule est demandée par le sujet)

Q4. Indiquer la teinte de la forme acide de l’indicateur coloré.

Le sujet indique « On ajoute quelques gouttes de teinture de tournesol et l’on verse de l’eau de baryte avec une burette graduée jusqu’à ce que la teinte rose du tournesol ait viré au bleu franc. »
Au début du dosage, seul l’acide éthanoïque est présent dans l’erlenmeyer.
Ainsi, la teinte de la forme acide de l’indicateur coloré est la teinte du début du titrage : teinte rose

On considère une solution titrante de concentration en quantité de matière c_B en ions hydroxyde HO⁻(aq) de valeur égale à 2,0 mol·L^–1 et provoquant le changement de couleur pour un volume V_BE versé à l’équivalence de valeur égale à 5,0 mL.

Q5. En utilisant la relation entre les quantités de matière à l’équivalence, calculer la valeur de la quantité de matière n_A en acide éthanoïque dans l’échantillon titré.

$${\rm CH}_3CO_2H\left(l\right)+{\rm HO}^-\left(aq\right)\longrightarrow{\rm CH}_3CO_2^-\left(aq\right)+H_2O(l)$$
A l’équivalence, les réactifs sont introduits dans les proportions stœchiométriques :
$$\frac{n{{\rm CH}_3CO_2H}^i}{1}=\frac{n{HO^-}^{eq}}{1}$$
$$n{{\rm CH}_3CO_2H}^i=C_B\times V{BE}$$
$$n_A=C_B\times V_{BE}$$
$$n_A=2,0\times5,0\times{10}^{-3}$$
$$n_A=1,0\times{10}^{-2}\ mol$$

Données :

• Le volume de l’échantillon V_éch vaut un centième du volume du mélange réactionnel initial V_i ;
• Le dosage par titrage réalisé a montré que 10 % de l’acide initial avait réagi.

Q6. Montrer que ce mélange contenait initialement une quantité de matière d’acide n_i de valeur égale à 1,1 mol.

Le dosage par titrage réalisé a montré que 10 % de l’acide initial avait réagi : il reste donc 90% d’acide.
Ainsi, $n_A=1,0\times{10}^{-2}\ mol$ représente les 90% d’acide restant.

90 %	$1,0\times{10}^{-2}\ mol$
100 %	$n_{A,\ ini\ ech}$

$$n_{A,\ ini\ ech}=\frac{100\times1,0\times{10}^{-2}}{90}$$
$$n_{A,\ ini\ ech}=1,1\times{10}^{-2}\ mol$$

Or, Le volume de l’échantillon $V_{ech}$ vaut un centième du volume du mélange réactionnel initial $V_i$. La quantité de matière d’acide $n_i$ est donc 100 fois plus grande que la quantité de matière d’acide $n_{A,\ ini\ ech}$ présente dans l’échantillon :
$$n_i=100\times n_{A,\ ini\ ech}$$
$$n_i=100\times1,1\times{10}^{-2}$$
$$n_i=1,1\ mol$$

Ainsi, ce mélange contenait initialement une quantité de matière d’acide $n_i$ de valeur égale à 1,1 mol.

2.    Cinétique chimique.

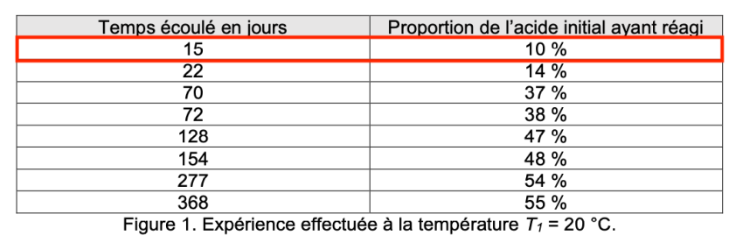
Les dosages par titrage successifs d’échantillons issus du mélange réactionnel laissé à température ambiante ont permis d’obtenir les résultats du tableau de la figure 1.

Temps écoulé en jours	Proportion de l’acide initial ayant réagi
15	10 %
22	14 %
70	37 %
72	38 %
128	47 %
154	48 %
277	54 %
368	55 %

Figure 1. Expérience effectuée à la température T₁ = 20 °C.

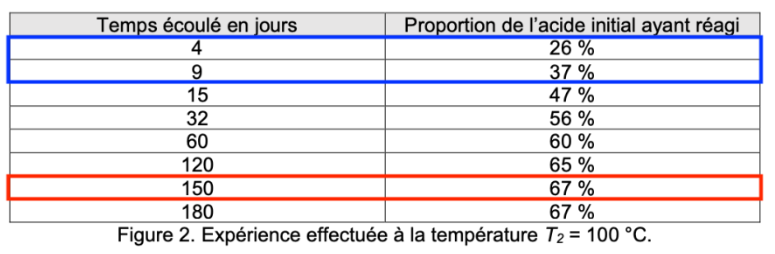
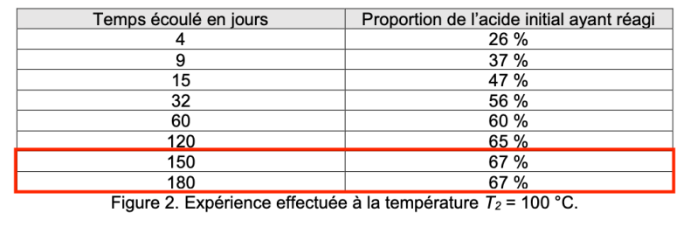
L’expérience a été reproduite en portant la température T₂ du mélange réactionnel à la valeur constante égale à 100 °C. Les résultats obtenus sont présentés dans le tableau de la figure 2.

Temps écoulé en jours	Proportion de l’acide initial ayant réagi
4	26 %
9	37 %
15	47 %
32	56 %
60	60 %
120	65 %
150	67 %
180	67 %

Figure 2. Expérience effectuée à la température T₂ = 100 °C.

Q7. Expliquer pourquoi l’ensemble des mesures de Marcellin Berthelot illustrent le fait que la température est un facteur cinétique. Au moins une comparaison quantitative s’appuyant sur les données des tableaux des figures 1 et 2 est attendue.

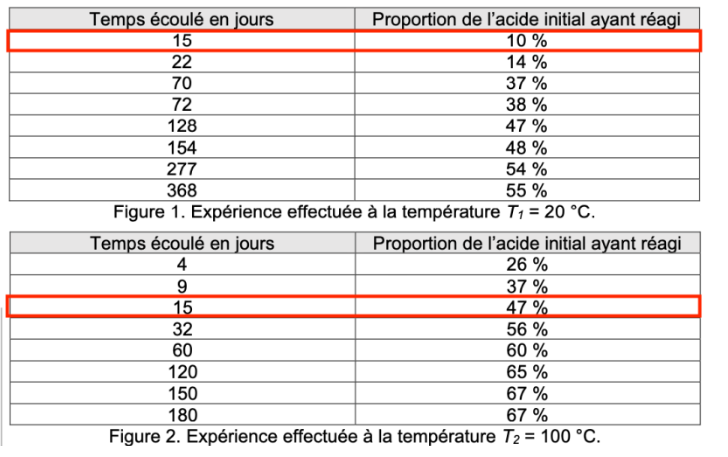
Q8. Définir le temps de demi-réaction t_1/2 d’une transformation chimique. Pour l’expérience à la température T₂, donner l’encadrement de la valeur de t_1/2 le plus précis possible selon les données de la figure 2, sachant que l’état final est atteint après 150 jours.

Q9. À l’aide du tableau de la figure 1 et de la quantité de matière initiale d’acide ni, montrer qu’après les quinze premiers jours de l’expérience à température ambiante la valeur de la quantité de matière d’acide restant est égale à une mole.

Données :

• Vitesse volumique moyenne de disparition d’un réactif : $v=\frac{c_{initiale}-c_{finale}}{\Delta t}$ ;
• Volume initial du mélange réactionnel : V_mélange = 130 mL.

Q10. Calculer la valeur moyenne v de la vitesse volumique de disparition de l’acide, à température ambiante, sur la durée Δt = 15 j. Le résultat sera exprimé en mol·L^–1·j^–1.

Calculons la valeur moyenne $v$ de la vitesse volumique de disparition de l’acide, à température ambiante, sur la durée $\Delta t=15\ j$ :
D’après les données :
$$v=\frac{c_{initiale}-c_{finale}}{\Delta t}$$
Or
$$c_{initiale}=\frac{n_{initiale}}{V_{melange}}$$
$$c_{finale}=\frac{n_{finale}}{V_{melange}}$$

D’où
$$v=\frac{\frac{n_{initiale}}{V_{melange}}-\frac{n_{finale}}{V_{melange}}}{\Delta t}$$
$$v=\frac{\frac{1,1}{130\times{10}^{-3}}-\frac{1,0}{130\times{10}^{-3}}}{15}$$
$$v=0,051\ mol\cdot L^{-1}\cdot j^{-1}$$
$$v=5,1\times{10}^{-2}\ mol\cdot L^{-1}\cdot j^{-1}$$

Q11. Expliquer sans calcul comment évolue ensuite la vitesse de disparition de l’acide dans l’expérience se déroulant à 20 °C. Justifier ce comportement à l’aide d’un facteur cinétique autre que la température.

Plus la réaction évolue, plus la concentration restante d’acide diminue.
Or la concentration est un facteur cinétique et lorsque la concentration des réactifs diminue, la vitesse de disparation diminue.
Ainsi, la vitesse de disparition de l’acide dans l’expérience se déroulant à 20 °C diminue au cours du temps.

Q12. Proposer une modification du protocole qui permettrait d’accélérer la réaction d’estérification sans changer la température du mélange réactionnel.

Pour accélérer la réaction d’estérification sans changer la température du mélange réactionnel, on peut augmenter la concentration des réactifs.

3.   Équilibre chimique.

Les expériences décrites dans les deux tableaux précédents ont été prolongées bien au-delà des durées qui y sont indiquées : elles ont montré que le mélange réactionnel n’évoluait plus lorsque 67 % de la quantité de matière d’acide initial avait réagi, quelle que soit sa température.

Dans le mémoire Recherche sur les affinités (1862-1863), Marcellin Berthelot a ainsi pu écrire :

« Il résulte de ces expériences que toutes les fois que l’action d’un acide sur un alcool a été suffisamment prolongée, ou réalisée à une température suffisamment élevée, la composition des systèmes devient sensiblement invariable. On voit en même temps que l’état d’équilibre qui se produit ainsi ne répond jamais à une saturation complète de l’acide par l’alcool ».

Q13. Expliquer, en utilisant la notion d’avancement, la différence entre une réaction totale et une réaction menant à un équilibre chimique. Indiquer l’expression qu’utilise Marcellin Berthelot dans le texte ci-dessus pour parler d’une réaction totale.

Dans une réaction totale, les réactifs sont entièrement consommés, donc l’avancement $x_f$ atteint son maximum $x_f=x_{max}$.

Dans une réaction menant à un équilibre chimique, les réactifs et les produits coexistent : l’avancement s’arrête à une valeur $x_f<x_{max}$ : la réaction directe et la réaction inverse s’équilibrent, sans consommation totale des réactifs.
L’expression qu’utilise Marcellin Berthelot dans le texte ci-dessus pour parler d’une réaction totale est « saturation complète »

Q14. Préciser en quoi le tableau de la figure 2 de mesures à la température T₂ permettait déjà de soupçonner l’existence d’un équilibre chimique pour la réaction d’estérification. Citer une partie du texte ci-dessus évoquant l’intérêt de mener l’expérience à la température T₂ de valeur égale à 100 °C.

Données :

• On rappelle l’équation de la réaction modélisant la transformation étudiée : CH₃COOH(ℓ) + C₂H₅OH (ℓ) ⇄ CH₃COOC₂H₅ (ℓ) + H₂O(ℓ)
• On considère un mélange réactionnel initial de volume V_mélange = 130 mL à une température T de valeur égale à 25°C, contenant des quantités de matière identiques en acide et en alcool : n_acide = n_alcool = 1,1 mol ;
• Concentration standard en quantité de matière à 25°C : c° = 1,0 mol·L^–1 ;
• L’eau n’étant pas le solvant, sa concentration en quantité de matière intervient dans l’expression du quotient de réaction.

Q15. Justifier que les concentrations en quantité de matière des quatre espèces chimiques en présence dans l’état d’équilibre ont pour valeur :

[CH₃COOH]éq = [C₂H₅OH]éq = 2,8 mol·L^–1 ;
[CH₃COOC₂H₅]éq = [H₂O]éq = 5,7 mol·L^–1.

		${\rm CH}_3COOH$	$+ C_2H_5OH \rightleftarrows $	${\rm CH}_3COOC_2H_5(l)$	$+\ H_2O(l)$
État initial	x = 0	$n_{acide}$	$n_{alcool}$	0	0
État intermédiaire	x	$n_{acide}-x$	$n_{alcool}-x$	$x$	$x$
État final	x=xf	$n_{acide}-x_f$	$n_{alcool}-x_f$	$x_f$	$x_f$

D’après l’énoncé : « le mélange réactionnel n’évoluait plus lorsque 67 % de la quantité de matière d’acide initial avait réagi, quelle que soit sa température. » : il reste donc $100-67=33%$ de la quantité de matière d’acide initial
On a donc :
$$n_{acide,\ restant}=0,33\times n_{acide}$$
Or $n_{acide,\ restant}=n_{acide}-x_f$
$$n_{acide}-x_f=0,33\times n_{acide}$$
$$-x_f=0,33\times n_{acide}-n_{acide}$$
$$x_f=-0,33\times n_{acide}+n_{acide}$$
$$x_f=-0,33\times1,1+1,1$$
$$x_f=0,74\ mol$$

Calculons les concentrations en quantité́ de matière des quatre espèces chimiques en présence dans l’état d’équilibre :
$$\left[{\rm CH}_3COOH\right]{eq}=\frac{n_{{\rm CH}_3COOH}^{eq}}{V{melange}}$$
$$\left[{\rm CH}_3COOH\right]{eq}=\frac{n_{acide}-x_f}{V_{melange}}$$
$$\left[{\rm CH}_3COOH\right]{eq}=\frac{1,1-0,74}{130\times{10}^{-3}}$$
$$\left[{\rm CH}_3COOH\right]{eq}=2,8\ mol\cdot L^{-1}$$

$$\left[C_2H_5OH\right]{eq}=\frac{n_{C_2H_5OH}^{eq}}{V_{melange}}$$
$$\left[C_2H_5OH\right]{eq}=\frac{n_{alcool}-x_f}{V_{melange}}$$
$$\left[C_2H_5OH\right]{eq}=\frac{1,1-0,74}{130\times{10}^{-3}}$$
$$\left[C_2H_5OH\right]{eq}=2,8\ mol\cdot L^{-1}$$

$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=\frac{n_{{\rm CH}_3COOC_2H_5}^{eq}}{V{melange}}$$
$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=\frac{x_f}{V_{melange}}$$
$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=\frac{0,74}{130\times{10}^{-3}}$$
$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=5,7\ mol\cdot L^{-1}$$

$$\left[H_2O\right]{eq}=\frac{n_{H_2O}^{eq}}{V_{melange}}$$
$$\left[H_2O\right]{eq}=\frac{x_f}{V_{melange}}$$
$$\left[H_2O\right]{eq}=\frac{0,74}{130\times{10}^{-3}}$$
$$\left[H_2O\right]{eq}=5,7\ mol\cdot L^{-1}$$

Ainsi :
$$\left[{\rm CH}_3COOH\right]{eq}=\left[C_2H_5OH\right]{eq}=2,8\ mol\cdot L^{-1}$$
$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=\left[H_2O\right]{eq}=5,7\ mol\cdot L^{-1}$$

Q16. À l’aide des données, établir l’expression du quotient de réaction Q de la réaction d’estérification. Indiquer sa valeur Q_i dans l’état initial, puis calculer sa valeur Q_éq = K dans l’état d’équilibre chimique.

$${\rm CH}_3COOH\left(l\right)\ \ \ +\ \ C_2H_5OH\left(l\right)\ \ \ \ \ \ \ \rightleftarrows\ \ \ {\rm CH}_3COOC_2H_5(l)\ +\ H_2O(l)$$
$$Q=\frac{\left[{\rm CH}_3COOC_2H_5\right]\times\left[H_2O\right]}{\left[{\rm CH}_3COOH\right]\times\left[C_2H_5OH\right]}$$

$$Q_i=\frac{\left[{\rm CH}_3COOC_2H_5\right]_i\times\left[H_2O\right]_i}{\left[{\rm CH}_3COOH\right]_i\times\left[C_2H_5OH\right]_i}$$
Or
$$\left[{\rm CH}_3COOC_2H_5\right]_i=0\ mol\cdot L^{-1}\ \text{et}\ \left[H_2O\right]_i=0\ mol\cdot L^{-1}$$
$$Q_i=\frac{0\times0}{\left[{\rm CH}_3COOH\right]_i\times\left[C_2H_5OH\right]_i}$$
$$Q_i=0$$

$$Q_{eq}=k=\frac{\left[{\rm CH}3COOC_2H_5\right]{eq}\times\left[H_2O\right]{eq}}{\left[{\rm CH}3COOH\right]{eq}\times\left[C_2H_5OH\right]{eq}}$$
Or
$$\left[{\rm CH}_3COOH\right]{eq}=\left[C_2H_5OH\right]{eq}=2,8\ mol\cdot L^{-1}$$
$$\left[{\rm CH}_3COOC_2H_5\right]{eq}=\left[H_2O\right]{eq}=5,7\ mol\cdot L^{-1}$$
$$Q_{eq}=k=\frac{5,7\times5,7}{2,8\times2,8}$$
$$Q_{eq}=k=4,1$$

Q17. Dans son mémoire, Marcellin Berthelot a présenté plusieurs méthodes permettant de faire réagir l’acide éthanoïque et l’éthanol avec un rendement supérieur à 67%. Proposer une méthode possible.

Pour augmenter le rendement, on peut séparer les produits formés. Ainsi, ils ne peuvent pas réagir entre eux et former les réactifs. Le quotient de réaction sera toujours nul et donc inferieur à $K$ : la réaction se déroulera dans le sens direct.