Bac Amérique du Sud 2022 Sujet 2
Exercice C – (5 points) – Au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n°22-PYCJ2AS1
Sujet et corrigé
EXERCICE C. LA BATTERIE AU LITHIUM – FER – PHOSPHATE D’UNE AUTOMOBILE
Mots-clés : quotient de réaction et sens d’évolution d’un système, réaction d’oxydo-réduction
Les batteries lithium-ion sont devenues une source d’électricité indispensable pour nos dispositifs électroniques portables et portatifs dont la taille ne cesse de se réduire. En outre, du fait de leurs avantages remarquables par rapport aux autres types de batteries, par exemple leur densité de stockage d’énergie supérieure, elles ont permis le développement d’un large éventail d’applications au-delà de leur cœur de cible technologique, notamment pour les véhicules hybrides et électriques.
https://cordis.europa.eu/article/id/242819-improved-lithiumion-batteries-to-boost-electric-vehicles/fr
Données :
- charge élémentaire : 𝑒 = 1,60 × 10−19 C ;
- constante d’Avogadro : 𝑁𝐴 = 6,02 × 1023 mol−1 ;
- équivalence ampère-heure / coulomb : 1,0 Ah = 3,6 × 103 C ;
- masses molaires : 𝑀(LiC6) = 78,9 g⋅mol−1 , 𝑀(FePO4) = 150,8 g⋅mol−1.
Caractéristiques de la batterie
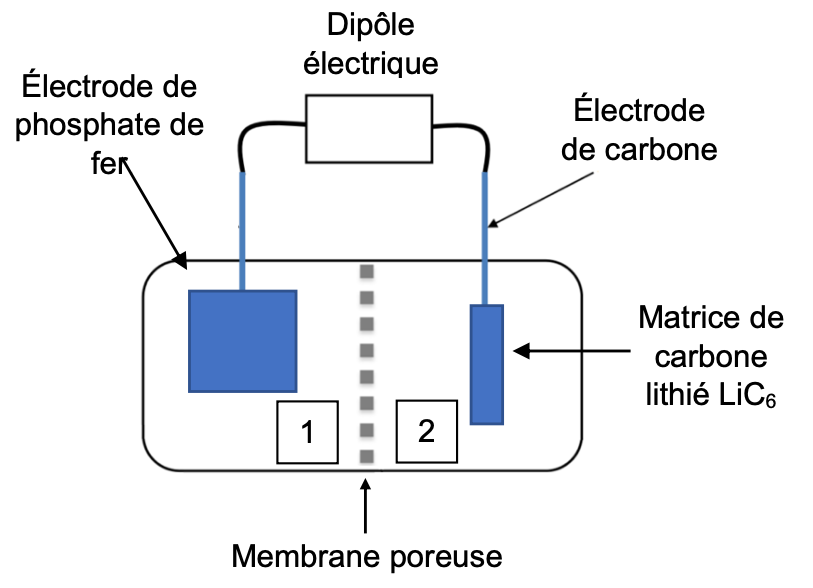
L’électrode de phosphate de fer, FePO4, du compartiment 1 a une masse 𝑚(FePO4) = 4,7 kg et lorsque la batterie est chargée, l‘électrode du compartiment 2 est recouverte d’une matrice de carbone lithié de formule LiC6 pesant 1,1 kg. Les électrodes plongent dans un électrolyte organique ionique contenant des ions lithium et les deux compartiments sont séparés par une membrane
Pour démarrer, la voiture nécessite une charge électrique 𝑞𝐷 = 45 Ah.
Lors de la décharge de la batterie, les transformations chimiques en jeu sont modélisables par deux réactions électrochimiques aux électrodes dont les équations figurent ci-dessous.
- Libération du lithium dans le compartiment 2 :
LiC6(s) = 6 C(s) + Li+ + e−
- Formation de phosphate de fer lithié de formule LiFePO4 :
Li+ + e− + FePO4(s) = LiFePO4(s)
1. Identifier l’électrode où se produit une oxydation et celle où se produit une réduction. Justifier.
Une réduction est un gain d’électrons.
${\rm Li}^++e^-+FePO_4(s)=LiFePO_4(s)$
Compartiment 1 : c’est la cathode.
Une oxydation est une perte d’électrons.
$LiC_6\left(s\right)=6C\left(s\right)+{\rm Li}^++e^-$
Compartiment 2 : c’est l’anode.
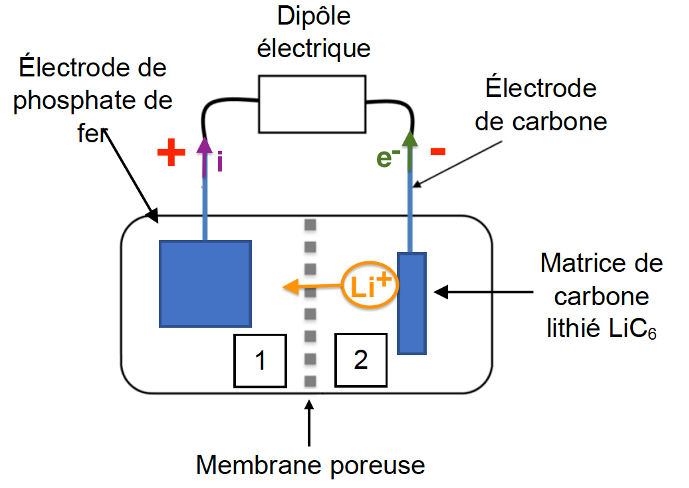
2. Reproduire le schéma de la pile, indiquer les polarités des électrodes et représenter les porteurs de charges et leur sens de circulation lorsque la pile débite.
Compartiment 2 : perte d’électrons donc elle constitue la borne négative et le compartiment 1 la borne positive.
Les électrons partent de l’anode (compartiment 2) vers la cathode (compartiment 1).
Le courant circule donc de la cathode (compartiment 1) vers l’anode (compartiment 2).
Lorsque la pile débite, les ions sont produits dans le compartiment 2 et sont consommés dans le compartiment 1.
3. Écrire l’équation de la réaction modélisant le fonctionnement de la pile.
Compartiment 1 : ${\rm Li}^++e^-+FePO_4(s)=LiFePO_4(s)$
Compartiment 2 : $LiC_6\left(s\right)=6C\left(s\right)+{\rm Li}^++e^-$
Equation de la réaction modélisant le fonctionnement de la pile :
${\rm Li}^++FePO_4\left(s\right)+LiC_6\left(s\right)\rightleftarrows LiFePO_4\left(s\right)+6C\left(s\right)+{\rm Li}^+$
${\rm Li}^++FePO_4\left(s\right)+LiC_6\left(s\right)\rightleftarrows LiFePO_4\left(s\right)+6C\left(s\right)+{\rm Li}^+$
$FePO_4\left(s\right)+LiC_6\left(s\right)\rightleftarrows LiFePO_4\left(s\right)+6C\left(s\right)$
4. La valeur de la constante d’équilibre de la réaction de fonctionnement de la pile à 25 °C vaut 𝐾 = 1054. Conclure quant à la transformation chimique mise en jeu dans la pile.
La valeur de la constante d’équilibre de la réaction de fonctionnement de la pile à 25 °C vaut $K=10^{54}$ :
$K>10^4$ la réaction est totale.
5. Montrer que la valeur de l’avancement final de la transformation est 𝑥max = 14 mol. Indiquer ce qu’il se passe lorsque cette valeur est atteinte lors du fonctionnement de la batterie ?
$n_{FePO_4}^i=\frac{m_{FePO_4}}{M_{FePO_4}}$
$n_{FePO_4}^i=\frac{4,7\times{10}^3}{150,8}$
$n_{FePO_4}^i=31\ mol$
$n_{LiC_6}^i=\frac{m_{LiC_6}}{M_{LiC_6}}$
$n_{FePO_4}^i=\frac{1,1\times{10}^3}{78,9}$
$n_{FePO_4}^i=14\ mol$
| $FePO_4\left(s\right)$ | $+LiC_6\left(s\right)\rightleftarrows$ | $ LiFePO_4\left(s\right)$ | $+6C\left(s\right)$ | |
| Etat initial | 31 | 14 | 0 | 0 |
| Etat intermédiaire | 31-x | 14-x | x | x |
| Etat final | 31-xf | 14-xf | xf | xf |
Calculons $x_{max}$ :
$31-x_{max1}=0$
$x_{max1}=31\ mol$
$14-x_{max2}=0$
$x_{max2}=14\ mol$
$x_{max2}<x_{max1}$
$x_{max}=x_{max2}=14\ mol$
Lorsque cette valeur est atteinte, la batterie cesse de fonctionner.
6. Déterminer la valeur de la capacité électrique maximale 𝑞max de cette batterie.
$q=n_{e^-}\times Na\times e$
$q_{max}=n_{e^-}^{max}\times Na\times e$
$q_{max}=x_{max}\times Na\times e$
$q_{max}=14\times6,02\times{10}^{23}\times1,60\times{10}^{-19}$
$q_{max}=1,3\times{10}^6\ C$
7. Indiquer si la batterie permet le démarrage du véhicule.
$1,0\ Ah=3,60\times{10}^3\ C$
$q_{max}=\frac{1,3\times{10}^6}{3,60\times{10}^3}$
$q_{max}=361\ Ah$
Pour démarrer, la voiture nécessite une charge électrique $q_D=45\ Ah$.
$q_{max}>q_D$
La batterie permet donc le démarrage du véhicule.
