Bac Asie 2023 Sujet 2
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°23-PYCJ2JA1
Sujet et corrigé
EXERCICE 1 ‒ L’IMPORTANCE DE LA VITAMINE C (9 POINTS)
L’acide ascorbique, communément appelé vitamine C, est un antioxydant présent dans de nombreux fruits et légumes.
La vitamine C est parfois utilisée dans des cosmétiques pour ses propriétés antioxydantes. Elle est aussi prescrite en complément alimentaire car elle joue un rôle important dans le métabolisme de l’être humain. Elle se dégrade à l’air, à la lumière et en présence d’oxydants.
L’objectif de l’exercice est d’étudier la dégradation de la vitamine C laissée à l’air libre dans un comprimé (partie A) ou dans un jus de fruit (partie B), puis d’examiner sa présence comme antioxydant dans les cosmétiques (partie C).
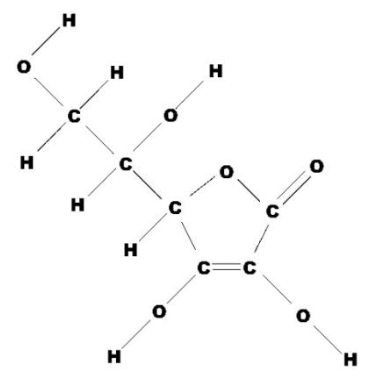
Source : Wikipédia
Données
- Formule développée de la molécule de vitamine C ou acide ascorbique, voir ci-contre.
- L’acide ascorbique C6H806 est un diacide possédant deux couples acido-basiques notés AH2/AH‒ et AH-/A2‒ dont les pKA respectifs sont : pKA1 = 4,1 et pKA2 = 11,8.
- Masse molaire de l’acide ascorbique : M = 176,1 g·mol-1.
- Conductivités molaires ioniques l° à 25 °C :
| ions | λ° en mS·m2·mol‒1 |
| Na+ | 5,01 |
| HO‒ | 19,9 |
| AH‒ | 3,42 |
- On rappelle que la conductivité s d’une solution se calcule à partir de la loi de Kohlrausch :
$$ \sigma=\sum_j \lambda_j^{0}\times[x_j] $$
où cj désigne une espèce chimique ionique et $ \lambda_j^{0}$ la conductivité molaire ionique de cette espèce.
- Concentration standard : c° = 1 mol·L-1.
Partie A – Dégradation de la vitamine C dans un comprimé
La vitamine C est commercialisée sous forme de comprimés à croquer. Ces comprimés sont conditionnés dans des tubes hermétiques et sous emballage protecteur. Cet emballage indique que chaque comprimé contient 250 mg d’acide ascorbique.
Un comprimé de vitamine C a été laissé plusieurs jours à l’air libre. La vitamine C qu’il contient a réagi avec le dioxygène de l’air.
On souhaite déterminer la masse d’acide ascorbique restant dans le comprimé à l’aide d’un titrage avec suivi conductimétrique d’une réaction acido-basique.
Une solution aqueuse SA est préparée par dissolution complète d’un comprimé de vitamine C dans l’eau. Le volume de la solution SA est V = 200,0 mL.
L’acide ascorbique et ses couples acide-base
- Parmi les trois propositions ci -dessous, indiquer celle qui correspond à la formule topologique de la vitamine C.
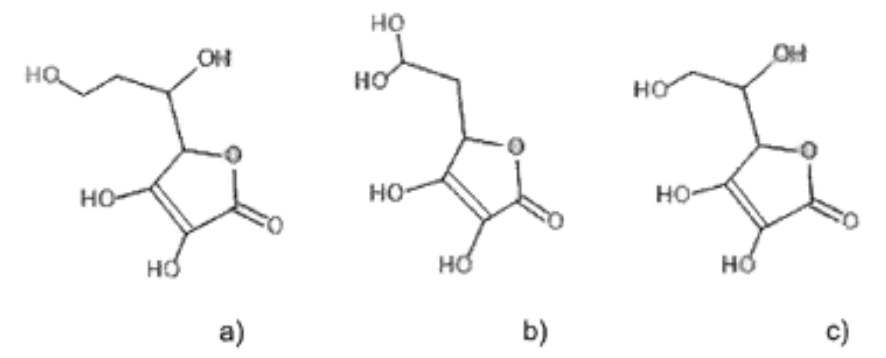
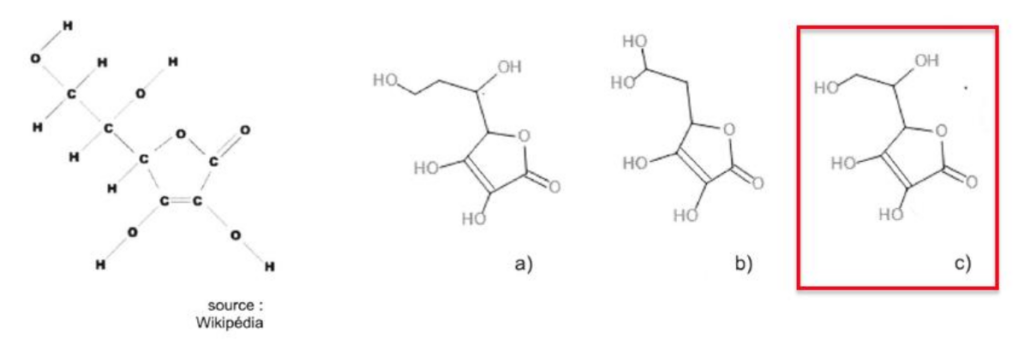
La proposition c est celle qui correspond à la formule topologique de la vitamine C.
Préparation de la solution titrante
Au laboratoire, on dispose d’une solution aqueuse d’hydroxyde de sodium de concentration C0 = 0,200 mol·L-1 et de la verrerie suivante :
- fioles jaugées de 20,0 mL, 25,0 mL, 50,0 mL, 100,0 mL, 200,0 mL, 250,0 mL, 500,0 mL,1000 mL ;
- pipettes jaugées de 1,0 mL, 5,0 mL, 10,0 mL, 20,0 mL.
2. Déterminer le volume V0 de solution d’hydroxyde de sodium de concentration C0 à prélever afin d’obtenir un volume VB = 200,0 mL de solution d’hydroxyde de sodium de concentration CB = 1,00×10-2 mol·L-1.
Lors d’une dilution la quantité de matière se conserve :
$$n_0=n_B$$
$$C_0\times V_0=C_B\times V_B$$
$$V_0=\frac{C_B\times V_B}{C_0}$$
$$V_0=\frac{1,00\times {10}^{-2}\times 200\times {10}^{-3}}{0,200}\ $$
$$V_0=1,00\times {10}^{-2}\ L\ $$
$$V_0=10,0\times {10}^{-3}\ L\ $$
$$V_0=10,0\ \ mL\ $$
3. Préciser la verrerie nécessaire pour mesurer V0 et VB.
Verrerie nécessaire pour mesurer V0 : pipette jaugée de 10,0 mL
Verrerie nécessaire pour mesurer VB : fiole jaugée de 200,0 mL.
Titrage de la solution SA
On prélève un volume VA = 20,0 mL de la solution aqueuse SA que l’on titre par une solution aqueuse d’hydroxyde de sodium (Na+, HO‒) de concentration CA = 1,00×10-2 mol·L-1.
Les couples acide-base mis en jeu sont AH2/AH‒ pour l’acide ascorbique et H2O/HO‒.
Le titrage acido-basique des 20,0 mL de solution SA par la solution d’hydroxyde de sodium de concentration CB = 1,00×10-2 mol·L-1 est réalisé. La conductivité de la solution est relevée en fonction du volume d’hydroxyde de sodium versé. La courbe de titrage est tracée figure 1 ci-après.
4. Écrire l’équation de la réaction support du titrage avec les notations simplifiées AH2, AH‒ et justifier qu’il s’agit d’une transformation acide-base au sens de Brønsted.
Couples :
$AH_2/AH^-$
$H_2O/{\rm HO}^-$
Équation de la réaction support du titrage :
$$AH_2(aq)+{\rm HO}^-(aq)\rightarrow AH^-(aq)+H_2O(l)$$
Lors de la réaction l’acide AH_2 cède un proton H^+ à la base ${\rm HO}^-$ : c’est une transformation acide-base au sens de Bronsted.
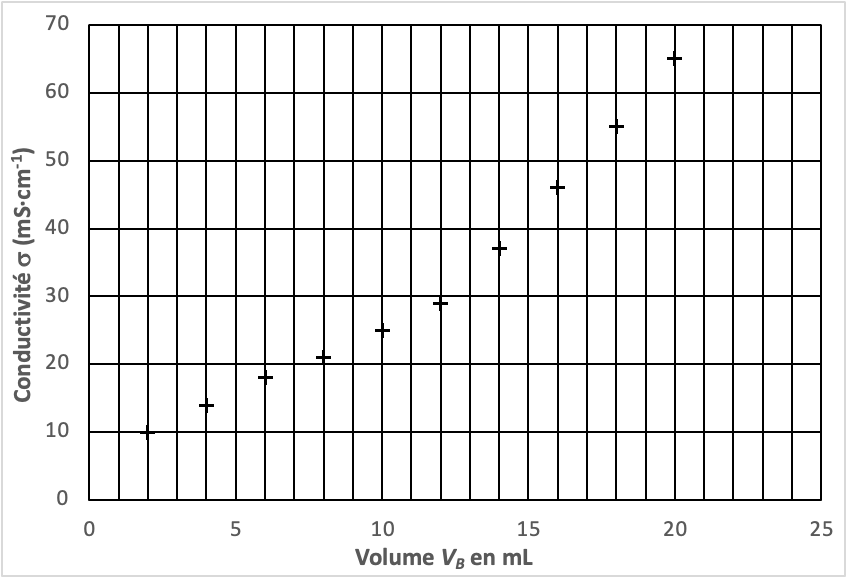
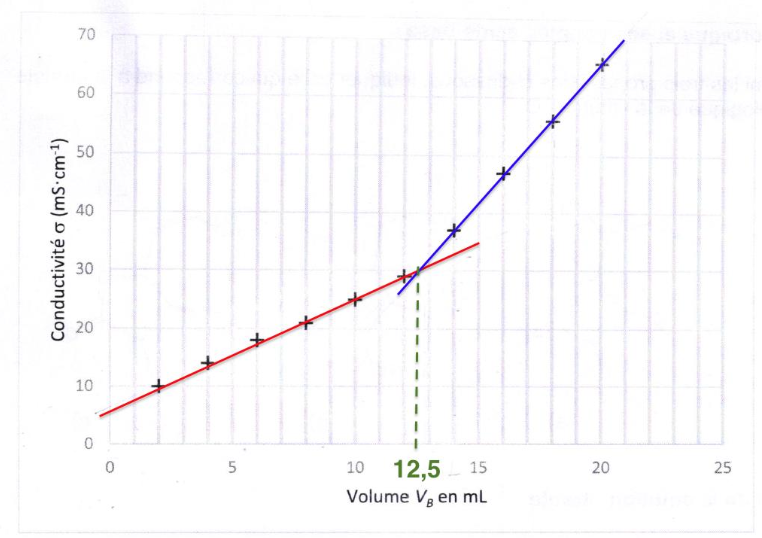
Figure 1 – Conductivité de la solution en fonction du volume de solution d’hydroxyde versé
5. Justifier le changement de pente observé sur le graphique, en s’appuyant sur les conductivités molaires ioniques.
$$AH_2(aq)+{\rm HO}^-(aq)\rightarrow AH^-(aq)+H_2O(l)$$
Avant l’équivalence :
$\left[{\rm AH}^-\right]$ augmente car c’est un produit de la réaction.
$\left[HO^-\right]$ est nulle car les ions $HO^-$ sont en défaut avant l’équivalence
$\left[{\rm Na}^+\right]$ augmente car les ions ${\rm Na}^+$sont spectateurs et ajoutés au cours du titrage.
| Ions | Avant l’équivalence |
| $${\rm AH}^-$$ | ↗ |
| $$HO^-$$ | 0 |
| $${\rm Na}^+$$ | ↗ |
Apres l’équivalence :
$\left[{\rm AH}^-\right]$ reste car constant. ${\rm AH}^-$est un produit de la réaction or après l’équivalence, il n’y a plus de réaction entre $AH_2\left(aq\right)\ et\ {\rm HO}^-(aq)$ car tous les AH_2 ont été consommés.
$\left[HO^-\right]$ augmente car les ions HO^- sont en excès après l’équivalence et ils ne réagissent plus
$\left[{\rm Na}^+\right]$ augemente car les ions ${\rm Na}^+$sont spectateurs et ajoutés au cours du titrage.
| Ions | Apres l’équivalence |
| $${\rm AH}^-$$ | = |
| $$HO^-$$ | ↗ |
| $${\rm Na}^+$$ | ↗ |
Avant l’équivalence, la concentration des ions augmente donc la conductivité augmente.
Apres l’équivalence, la concentration des ions augmente donc la conductivité augmente.
Comparons les deux augmentations :
$$\lambda_{HO^-}>\lambda_{{\rm AH}^-}$$ donc l’augmentation de la conductivité est plus importante après l’équivalence.
6. Déterminer le volume VBE à l’équivalence.
La valeur du volume à l’équivalence VBE se lit à l’intersection des deux droites :
Graphiquement VBE = 12,5 mL
7. En déduire la valeur de la masse m de vitamine C dans le comprimé resté à l’air libre et vérifier que cette valeur est comprise entre 190 mg et 230 mg.
A l’équivalence :
$$\frac{n_{AH_2}^i}{1}=\frac{n_{HO^-}^{eq}}{1}$$
$$\frac{m_{AH_2}}{M_{AH_2}}=C_B\times V_{BE}$$
$$m_{AH_2}=C_B\times V_{BE}\times M_{AH_2}$$
$$m_{AH_2}=1,00\times {10}^{-2}\times 12,5\times {10}^{-3}\times 176,1$$
$$m_{AH_2}=2,2\times {10}^{-2}\ g$$
$$m_{AH_2}=22\times {10}^{-3}\ g$$
$$m_{AH_2}=22\ mg$$
D’après l’énoncé : « Une solution aqueuse SA est préparée par dissolution complète d’un comprimé de vitamine C dans l’eau. Le volume de la solution SA est V = 200,0 mL. »
Or on a dosé VA = 20,0 mL.
| 22 mg | 20,0 mL |
| m | 200,0 mL |
$$m=\frac{200,0\times 22}{20,0}$$
$$m=220\ mg$$
La valeur de la masse m de vitamine C dans le comprimé resté à l’air libre est bien comprise entre 190 mg et 230 mg.
8. Justifier, à partir de l’information fournie par l’emballage au sujet de chaque comprimé, qu’une réaction de la vitamine C a bien eu lieu.
D’après l’énoncé : « Cet emballage indique que chaque comprimé contient 250 mg d’acide ascorbique. »
Le dosage indique que le comprimé ne contient plus que 220 mg d’acide ascorbique. Cet écart s’explique par une réaction de la vitamine C du comprimé avec le dioxygène de l’air.
Partie B – Étude cinétique de la dégradation de la vitamine C dans un jus d’orange
« La vitamine C est la plus fragile de toutes les vitamines : elle se dégrade rapidement à la chaleur, à l’eau, à l’air et à la lumière. Par exemple, à température ambiante, la moitié de la teneur en vitamine C d’un jus de fruit peut être perdue en 24 heures.
En conséquence, les modes de stockage doivent être adaptés de manière à limiter les pertes : les industriels conservent les produits à basse température (inférieure à 5 °C) en y adjoignant des agents actifs. »
D’après l’AFSSA – Agence Française de Sécurité Sanitaire des Aliments
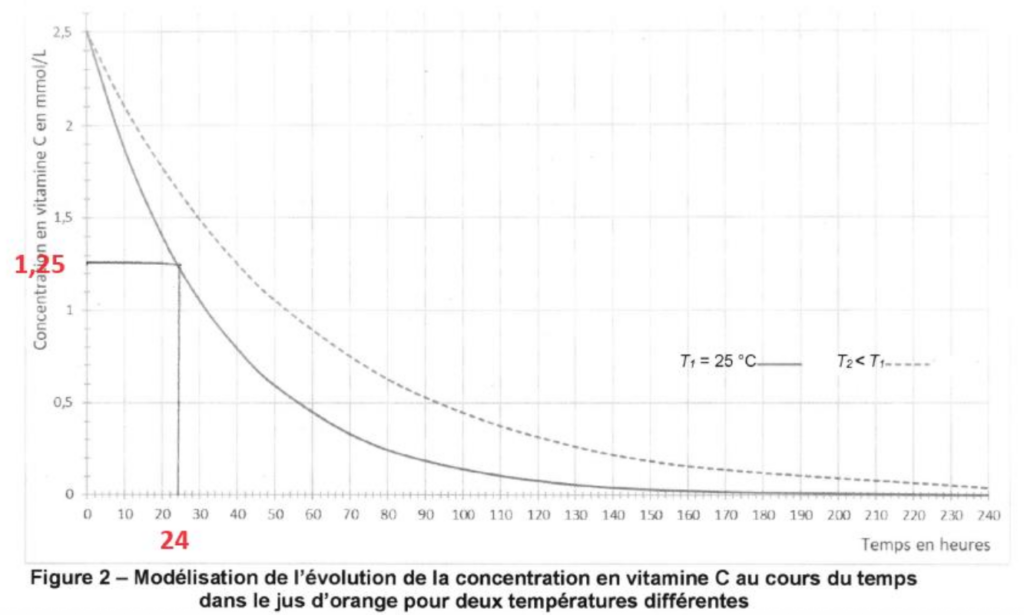
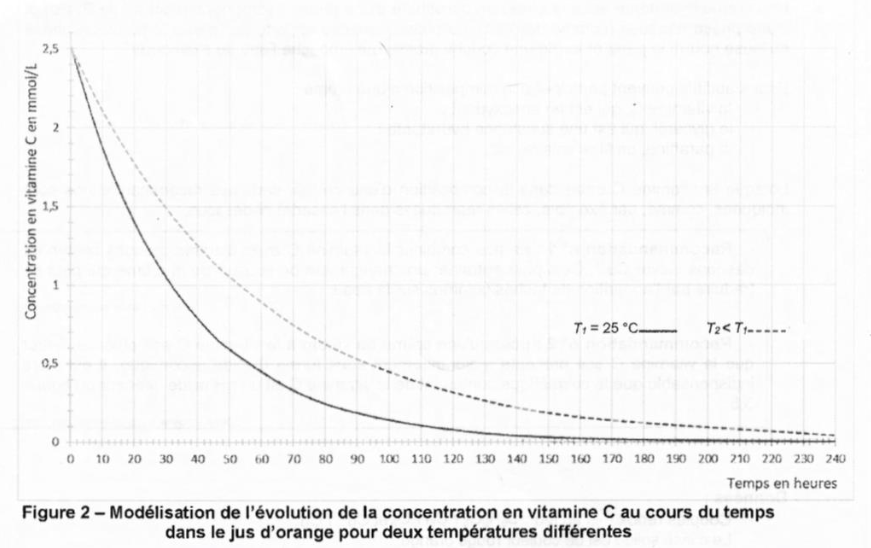
On dispose d’un jus d’orange filtré à la température T1 = 25 °C. À partir de données expérimentales, on a modélisé le suivi cinétique de la dégradation de la vitamine C, ou acide ascorbique, dans ce jus d’orange et à cette température (voir figure 2 ci-dessous).
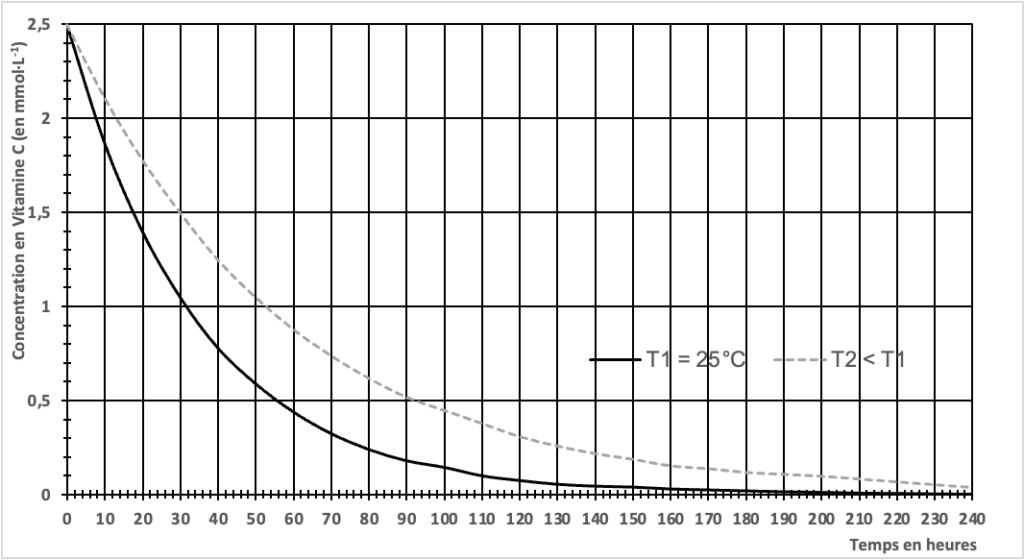
Figure 2 – Modélisation de l’évolution de la concentration en vitamine C au cours du temps dans le jus d’orange pour deux températures différentes
Données
- L’acide ascorbique est aussi un réducteur et fait partie du couple : C6H6O6 (aq) / C6H8O6(aq).
- Le dioxygène est l’oxydant du couple O2(g) / H2O(l).
9. Écrire les demi-équations correspondant aux couples mis en jeu lors de la dégradation de la vitamine C par le dioxygène de l’air et montrer que l’équation de l’oxydation de la vitamine C s’écrit :
2 C6H8O6 (aq) + O2(g) → 2 C6H6O6(aq) + 2 H2O(l)
Couples :
$$C_6H_6O_{6(aq)}/C_6H_8O_{6(aq)}$$
$$O_{2(g)}/H_2O_{(l)}$$
Demi-équations :
$$2\times\ \ C_6H_8O_{6(aq)}=C_6H_6O_{6(aq)}+2H^++2e^-$$
$$O_{2(g)}+4H^++4e^-=2H_2O_{(l)}$$
Équation de l’oxydation de la vitamine C :
$$2\ C_6H_8O_{6(aq)}+O_{2(g)}+4H^+=2\ C_6H_6O_{6(aq)}+4H^++2H_2O_{(l)}$$
$$2\ C_6H_8O_{6(aq)}+O_{2(g)}=2\ C_6H_6O_{6(aq)}+2H_2O_{(l)}$$
10. Définir la vitesse volumique de disparition de la vitamine C.
$$v_d=-\frac{d\left[C_6H_8O_6\right]_{(t)}}{dt}$$
11. À partir du graphique de la figure. 2, décrire qualitativement l’évolution de la vitesse de disparition de la vitamine C en fonction du temps, à une température donnée, et faire le lien avec un facteur cinétique à préciser.
$$v_d=-\frac{d\left[C_6H_8O_6\right]_{(t)}}{dt}$$
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
La valeur absolue de la pente décroit au cours du temps. Ainsi la vitesse de disparation de la vitamine C diminue au cours du temps.
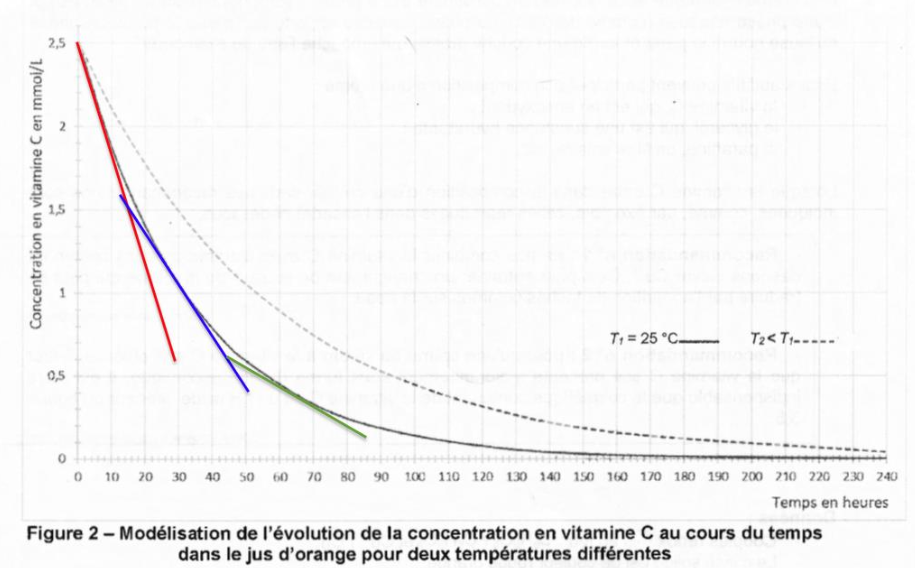
Le facteur cinétique responsable de cette diminution est la concentration. Au fur et à mesure de la disparation de la vitamine C, la concentration de la vitamine C diminue. Or plus la concentration est faible, plus la vitesse est petite.
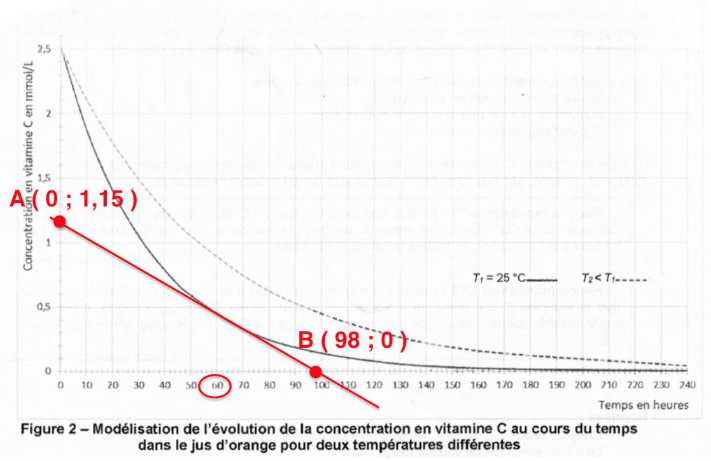
12. Déterminer graphiquement la vitesse volumique de disparition de la vitamine C à la température T1 = 25 °C à la date t1 = 60 h. L’exprimer en mmol·L-1·h-1.
$$v_d=-\frac{d\left[C_6H_8O_6\right]_{(t)}}{dt}$$
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
Pour t=60h :
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{0-1,15}{98-0}=-1,2.{10}^{-2}mmol.L^{-1}.h^{-1}$$
$$v_{t=60h}=-\frac{d\left[C_6H_8O_6\right]{(t)}}{dt}=-k$$
$$v{t=60h}=1,2.{10}^{-2}mmol.L^{-1}.h^{-1}$$
13. Déterminer graphiquement le temps t½ de demi-réaction à la température T1 = 25 °C et vérifier que cette valeur est cohérente avec celle annoncée dans le texte introductif de la partie B.
t1/2 est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : x(t1/2) = xf/2
$$C_{t_{1/2}}=\frac{C_0}{2}$$
Graphiquement : t1/2 = 24 h La valeur est cohérente avec celle annoncée dans le texte introductif de la partie B : « à température ambiante, la moitié de la teneur en vitamine C d’un jus de fruit peut être perdue en 24 heures
14. À partir de la figure 2, en comparant les deux courbes, donner un deuxième facteur cinétique, et indiquer pourquoi il est préférable de ne pas laisser le jus d’orange sur la table du petit déjeuner.
Graphiquement pour T2<T1, la concentration diminue moins rapidement.
Le facteur cinétique responsable de cette différence est la température : plus la température est élevée, plus la réaction est rapide.
Le jus d’orange sur la table se réchauffe, or plus la température est élevée, plus la réaction de disparation de la vitamine C est rapide. C’est pourquoi il est préférable de ne pas laisser le jus d’orange sur la table du petit déjeuner.
Partie C – Vitamine C dans les crèmes
Une crème hydratante est une émulsion constituée d’une phase hydrophobe (comme de l’huile) et d’une phase aqueuse (comme de l’eau). La phase aqueuse apporte de l’eau à la peau. La phase huileuse nourrit la peau et forme une couche grasse qui empêche l’eau de s’évaporer.
Divers additifs peuvent participer à la composition d’une crème :
- la vitamine C, qui est un antioxydant ;
- le glycérol, qui est une substance hydratante ;
- la paraffine, un filtre solaire, etc.
Lorsque la vitamine C entre dans la composition d’une crème, certaines recommandations sont indiquées, comme, par exemple, celles reproduites dans l’encadré ci -dessous.
- Recommandation n° 1 : ne pas combiner la vitamine C avec d’autres produits contenant des ions cuivre Cu2+. Cela peut entrainer un changement de couleur de la crème qui peut se traduire par l’apparition de taches colorées sur la peau.
D’après : www.cosmopolitan.fr
- Recommandation n° 2 : pour qu’une crème ou sérum à la vitamine C soit efficace, il faut que la vitamine C soit présente majoritairement sous forme d’acide ascorbique. Il est alors indispensable que le cosmétique contenant de la vitamine C ait un pH acide inférieur ou égal à 3,5.
D’après : www.medecine-anti-aae.com
Données :
- Couples rédox mis en jeu : C6H6O6 / C6H8O6 et Cu2+ / Cu.
- Le cuivre solide est de couleur rouge orangé.
L’équation de l’oxydation de la vitamine C par l’ion Cu2+ s’écrit :
C6H8O6(aq) + Cu2+(aq) → C6H6O6 (aq) + Cu(s) + 2 H+(aq)
15. Justifier le fait que des taches colorées peuvent apparaître, comme indiqué dans la recommandation n° 1.
C6H8O6(aq) + Cu2+(aq) → C6H6O6 (aq) + Cu(s) + 2 H+(aq)
L’équation de l’oxydation de la vitamine C par l’ion Cu2+ produit cuivre solide est de couleur rouge orangé.
D’où l’apparition des taches colorées comme indiqué dans la recommandation n°1.
16. Établir le diagramme de prédominance pour les couples AH2/AH‒ et AH‒/A2‒.
Diagramme de prédominance :

17. Évaluer la valeur du rapport $\frac{[AH_2]}{[AH^-]} $ pour la valeur de pH indiquée et justifier la recommandation n° 2 portant sur une valeur de pH à ne pas dépasser.
Le candidat est invité à présenter sa démarche et à faire preuve d’esprit critique.
$$pH=pK_{a1}+log\left(\frac{\left[AH^-\right]}{\left[AH_2\right]}\right)$$
$$pK_{a1}+log\left(\frac{\left[AH^-\right]}{\left[AH_2\right]}\right)=pH$$
$$log\left(\frac{\left[AH^-\right]}{\left[AH_2\right]}\right)=pH-pK_{a1}$$
$${10}^{log\left(\frac{\left[AH^-\right]}{\left[AH_2\right]}\right)}={10}^{pH-pK_{a1}}$$
$$\frac{\left[AH^-\right]}{\left[AH_2\right]}={10}^{pH-pK_{a1}}$$
$$\frac{\left[AH^-\right]}{\left[AH_2\right]}={10}^{3,5-4,1}$$
$$\frac{\left[AH^-\right]}{\left[AH_2\right]}=0,25$$
Ainsi,
$$\frac{\left[AH_2\right]}{\left[AH^-\right]}=\frac{1}{0,25}$$
$$\frac{\left[AH_2\right]}{\left[AH^-\right]}=4$$
$$\left[AH_2\right]>\left[AH^-\right]$$
La forme prédominante pour pH =3,5 est AH2.Si la valeur du pH augmente, le rapport augmente et la forme prédominante ne sera plus AH2.
C’est pourquoi, la recommandation n°2 porte sur un pH=3,5 à ne pas dépasser pour que la vitamine C soit présente majoritairement sous forme d’acide ascorbique.
