Bac Centres étrangers 2023 Sujet 1
Exercice 1 – (10 points) – Durée 1h45 – Calculatrice autorisée
Sujet n°25-PYCJ1G11
Sujet et corrigé
EXERCICE 1 – CONTROLE DE LA QUALITE D’UN BIBERON (9 points)
Chez le nourrisson, les ions nitrate (NO3 –) sont incriminés dans la survenue de la méthémoglobinémie (ou maladie bleue). La formation des ions nitrite, à partir des ions nitrate ingérés, est réalisée par la flore bactérienne intestinale. Chez les enfants, les ions nitrite en excès provoquent une moindre capacité des globules rouges à fixer et transporter l’oxygène.
C’est pourquoi la concentration en ions nitrate dans l’eau potable est réglementée, notamment pour la préparation des biberons […].

Source : Observatoire régional de la santé Rhône-Alpes, 2007
L’Organisation Mondiale de la Santé (OMS) a fixé la concentration maximale en ions nitrate dans l’eau à 50 mg·L-1.
Par ailleurs, indépendamment de la quantité d’ions nitrate, l’état de conservation d’un lait s’apprécie en mesurant son acidité.
Dans cet exercice, on se propose de :
- vérifier par deux méthodes différentes si une eau supposée potable prélevée au robinet satisfait ou non à la recommandation de l’OMS concernant les nitrates (partie A et partie B) ;
- déterminer combien de temps un biberon préparé peut être conservé avant consommation (partie C).
Partie A – Dosage spectrophotométrique des ions nitrate dans une eau
Par ajout d’acide 2,4-phénoldisulfonique, une solution aqueuse initialement incolore prend une teinte jaune plus ou moins prononcée selon sa concentration en ions nitrate NO3– . La concentration en ion NO3– de cette solution peut alors être déterminée par la mesure de son absorbance à une longueur d’onde donnée.
Données
- Absorption de la lumière du visible
| Longueurs d’onde d’absorption (nm) | 400 – 424 | 424 – 491 | 491 – 575 | 575 – 585 | 585 – 647 | 647 – 850 |
| Couleur absorbée | Violet | Bleu | Vert | Jaune | Orange | Rouge |
| Couleur complémentaire | jaune – vert | jaune | magenta | bleu | bleu – cyan | cyan |
- Protocole du dosage
ÉTAPE 1 : obtention d’une courbe d’étalonnage
Pour vérifier la concentration en masse en ions nitrate NO3– d’une eau, on réalise dans un premier temps plusieurs dilutions d’une solution aqueuse S de nitrate de potassium de concentration en masse tNO3– = 1,0 x 10-1 g·L-1 (avec ajout d’acide 2,4-phénoldisulfonique).
On obtient alors une échelle de teintes à partir de cinq solutions filles S1, S2, S3, S4 et S5 plus ou moins concentrées en ions nitrate.
On mesure ensuite l’absorbance A des différentes solutions filles à une longueur d’onde
l judicieusement choisie, puis on trace le graphe de l’absorbance A en fonction de la concentration en masse en ions nitrate tNO3– (figure 1 ci-dessous).
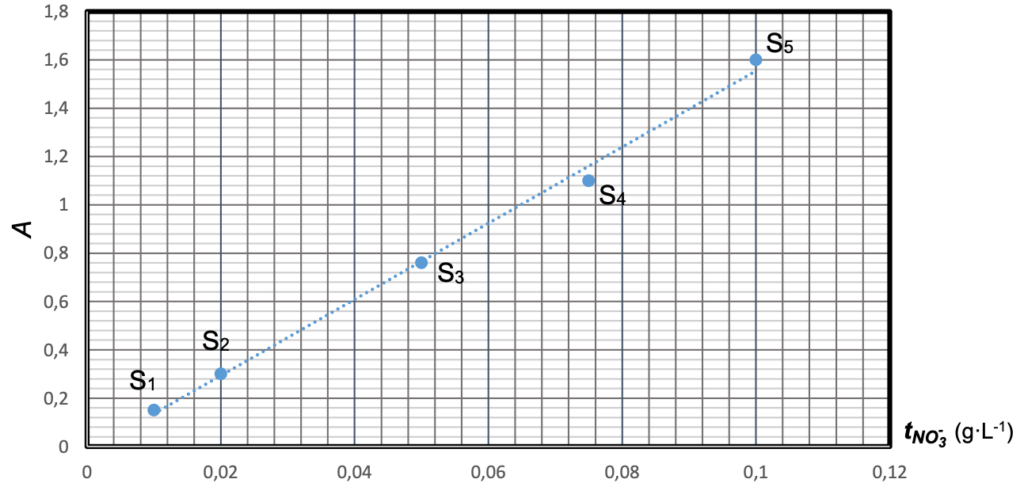
Figure 1. Courbe d’étalonnage des ions nitrate, NO3–
ÉTAPE 2 : mesure sur l’échantillon à analyser
On prélève un volume V = 250 mL de l’eau étudiée que l’on fait réagir avec un excès d’acide 2,4-phénoldisulfonique. On mesure ensuite l’absorbance de cette solution avec les mêmes réglages que ceux utilisés à l’ÉTAPE 1. L’absorbance mesurée est : A = 0,48.
Le spectrophotomètre utilisé lors de ce dosage peut fonctionner avec des radiations monochromatiques de longueurs d’onde : 440 nm, 510 nm, 580 nm, 640 nm.
1. Indiquer la longueur d’onde la plus adaptée pour réaliser ce dosage. Justifier.
D’après l’énoncé : « une solution aqueuse initialement incolore prend une teinte jaune »

Elle absorbe la couleur complémentaire : le bleu. Il faut donc $424\ nm<\lambda<491\ nm$.
Le spectrophotomètre utilisé lors de ce dosage peut fonctionner avec des radiations monochromatiques de longueurs d’onde : $440\ nm$, $510\ nm$, $580\ nm$, $640\ nm$.
La longueur d’onde la plus adaptée pour réaliser ce dosage est donc $\lambda=440\ nm$
2. Utiliser la figure 1 pour déterminer la concentration en masse en ions nitrate t1 de l’eau analysée.
L’absorbance mesurée est : $A = 0,48$.
Graphiquement :\ $t_1=0,032\ g{.L}^{-1}$
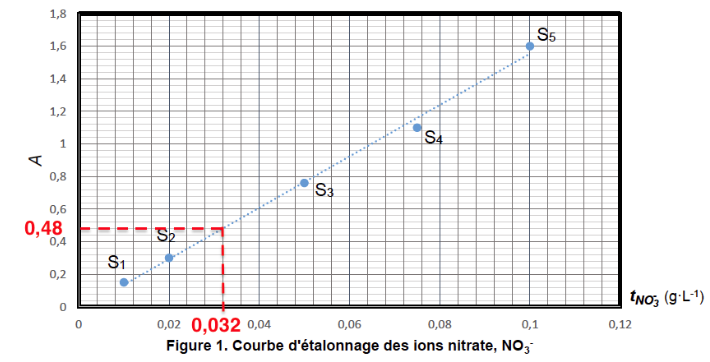
On désigne par u(t1) l’incertitude-type sur la valeur de t1. Pour cette détermination, on estime que l’incertitude-type relative $\frac{u(t_1)}{t_1} $ est de l’ordre de 15 %.
3. Écrire, en conservant un seul chiffre significatif pour l’incertitude-type, le résultat de la mesure de la concentration en ions nitrate t1.
$$\frac{u\left(t_1\right)}{t_1}=15%$$
$$u\left(t_1\right)=15%t_1$$
$$u\left(t_1\right)=\frac{15}{100}t_1$$
$$u\left(t_1\right)=\frac{15}{100}\times 0,032$$
$$u\left(t_1\right)=5\times {10}^{-3}g{.L}^{-1}$$
D’ou
$$t_1=0,032\ \pm5\times {10}^{-3}g{.L}^{-1}$$
$$t_1=\left(32\ \pm5\right)\times {10}^{-3}g{.L}^{-1}$$
$$t_1=32\pm 5\ mg{.L}^{-1}$$
Partie B – Dosage par titrage conductimétrique des ions nitrate dans l’eau étudiée
Une autre méthode de dosage consiste à faire réagir les ions nitrate, NO3– , en milieu acide, avec une quantité connue d’ions Fe2+. Cette quantité notée n(Fe2+)totale est largement suffisante pour consommer tous les ions nitrate : c’est l’étape 1.
On titre ensuite les ions Fe2+ en excès (qui n’ont pas réagi précédemment) à l’aide d’un dosage par titrage conductimétrique : c’est l’étape 2.
Données
- Masses molaires :
M(NO3– ) = 62,0 g·mol-1 ; M(Fe2+) = 55,8 g·mol-1 ; M(Cr2O72-) = 216 g·mol-1
- Protocole du titrage :
ÉTAPE 1 : on prélève un volume V = 250,0 ± 0,2 mL de l’eau étudiée dans la partie A. On fait réagir ce volume avec une solution acidifiée contenant n(Fe2+)totale = 4,0×10-3 mol d’ions Fe2+.
L’équation de la réaction est la suivante :
NO3– (aq) + 3 Fe2+(aq) + 4 H3O+(aq) → NO(g) + 3 Fe3+(aq) + 6 H2O(ℓ) (équation 1)
On note n(Fe2+)excès la quantité de matière en ions Fe2+ encore présente à l’état final de la réaction d’équation 1.
ÉTAPE 2 : la quantité de matière n(Fe2+)excès est déterminée à l’aide d’un titrage par les ions dichromate Cr2O72- d’une solution aqueuse de dichromate de potassium pour laquelle [Cr2O72-] = C = 5,0×10-2 ± 0,2×10-2 mol·L-1.
L’équation de la réaction support de ce titrage s’écrit :
Cr2O72-(aq) + 6 Fe2+(aq) + 14 H3O+(aq) → 2 Cr3+(aq) + 6 Fe3+(aq) + 21 H2O(ℓ) (équation 2)
La courbe du titrage obtenue est présentée dans la figure 2 ci-dessous.
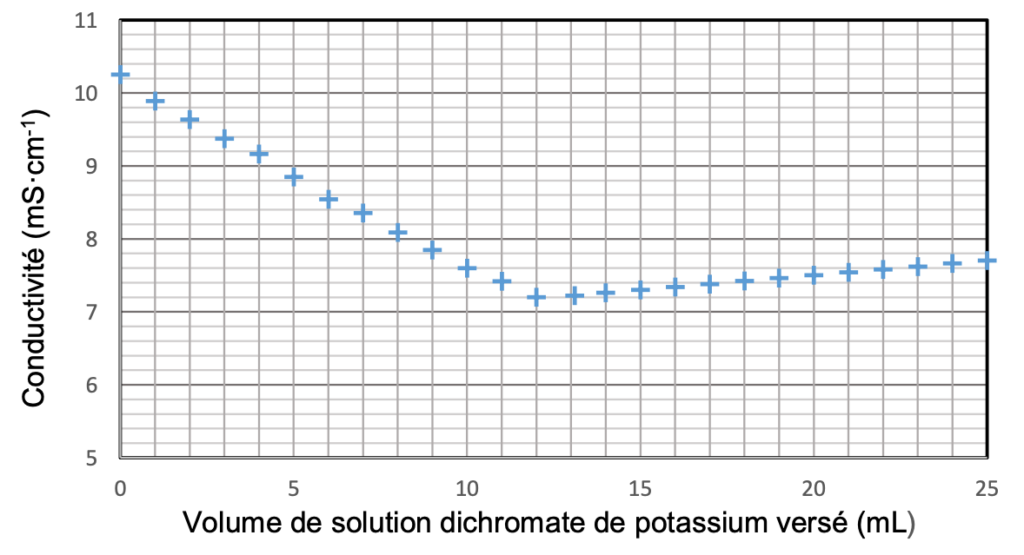
Figure 2. Courbe de titrage conductimétrique de l’eau analysée
4. Identifier le réactif titré et le réactif titrant lors du titrage de l’ÉTAPE 2.
Le réactif titré est celui qui est dosé : ${{\rm Fe}^{2+}}$
Le réactif titrant est celui de concentration connue : ${\rm Cr}_2O_7^{2-}$
5. À partir de l’exploitation de la figure 2, montrer que la quantité de matière des ions Fe2+ qui ont été versés en excès n(Fe2+)excès vaut environ 3,6 mmol.
$${\rm Cr}2O_7^{2-}\left(aq\right)+6{\rm Fe}^{2+}\left(aq\right)+14H_3O^+\left(aq\right)\rightarrow2{\rm Cr}^{3+}\left(aq\right)+6{\rm Fe}^{3+}\left(aq\right)+21H_2O\left(l\right)$$
A l’equivalence :
$$\frac{n(Fe^{2+}){excès}}{6}=\frac{n({\rm Cr}2O_7^{2-}){eq}}{1}$$
$$n(Fe^{2+}){excès}=6\times n({\rm Cr}2O_7^{2-}){eq}$$
$$n(Fe^{2+}){excès}=6\times C_{{\rm Cr}2O_7^{2-}}\times V{eq}$$
Graphiquement : $Veq=12,0\ mL$
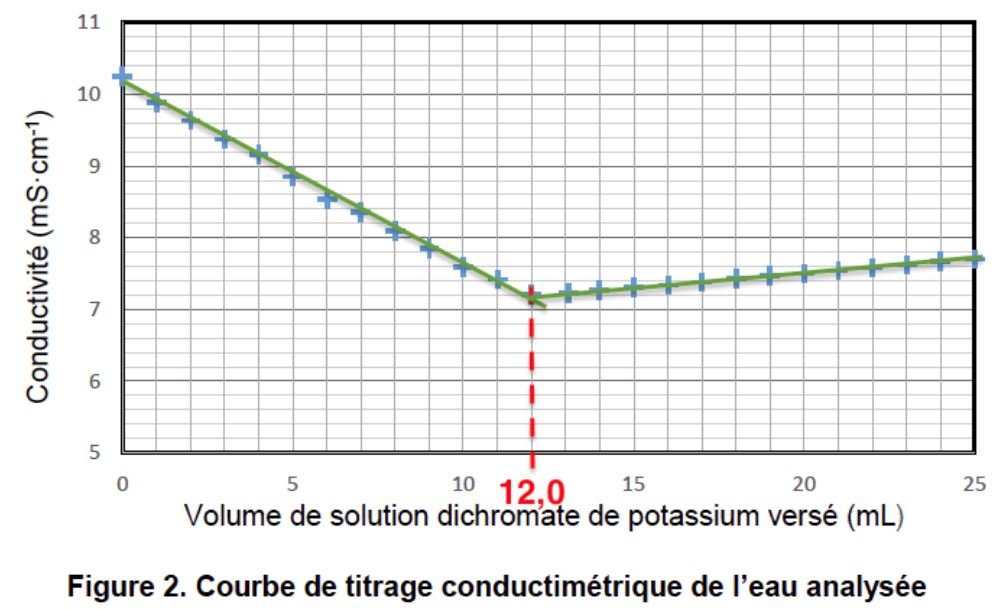
$$n(Fe^{2+}){excès}=6\times 5,0\times 10^{-2}\times 12,0\times 10^{-3}$$
$$n(Fe^{2+}){excès}=3,6\times 10^{-3}\ mol$$
$$n(Fe^{2+})_{excès}=3,6\ mmol$$
La quantité d’ions nitrate recherchée n(NO3– ) peut être calculée à partir de la quantité d’ions Fe2+ initialement introduite lors de l’ÉTAPE 1, n(Fe2+)totale, et à partir de la quantité d’ions Fe2+ titrée lors du titrage n(Fe2+)excès en utilisant la relation suivante :
$$ n(\mathrm{NO}3^-)=\frac{1}{3}\left[n(\mathrm{Fe}^{2+}){\text{totale}}-n(\mathrm{Fe}^{2+})_{\text{excès}}\right] $$
6. Justifier cette relation.
D’après l’énoncé : « Cette quantité notée n(Fe2+)totale est largement suffisante pour consommer tous les ions nitrate ». $NO_3^-$ est donc le réactif limitant.
| $NO_3^-(aq)$ | +$3{\rm Fe}^{2+}\left(aq\right)$ | +$4H_3O^+\left(aq\right)\rightarrow$ | $NO\left(g\right)$ | +$3{\rm Fe}^{3+}\left(aq\right)$ | +$6H_2O\left(l\right)$ | |
| État initial | $n\left(NO_3^-\right)$ | ${n\left({\rm Fe}^{2+}\right)}_{totale}$ | excès | 0 | 0 | Solvant |
| État intermédiaire | $n\left(NO_3^-\right)-x$ | ${n\left({\rm Fe}^{2+}\right)}_{totale}-3x$ | excès | x | 3x | Solvant |
| État final | $n\left(NO_3^-\right)-x_{max}=0$ | ${n\left({\rm Fe}^{2+}\right)}_{totale}-3x_{max}=n(Fe2+)_{excès}$ | excès | xf | 3xf | Solvant |
$${n\left({\rm Fe}^{2+}\right)}_{totale}-3x_{max}=n(Fe^{2+})_{excès}$$
$$n(Fe2+){excès}=n(Fe^{2+})_{totale}-3x_{max}$$
$$3x_{max}={n\left({\rm Fe}^{2+}\right)}_{totale}-n(Fe^{2+})_{excès}$$
$$x_{max}=\frac{1}{3}n(Fe^{2+})_{totale}-n(Fe^{2+})_{excès}$$
$$n\left(NO_3^-\right)-x_{max}=0$$
$$n\left(NO_3^-\right)=x_{max}$$
$$n\left(NO_3^-\right)=\frac{1}{3}n(Fe^{2+})_{totale}-n(Fe^{2+})_{excès}$$
7. Calculer la quantité d’ion nitrate n(NO3–) présente dans l’échantillon d’eau. En déduire que la concentration en masse en ion nitrate t2 vaut environ 33 mg·L-1.
$$n\left(NO_3^-\right)=\frac{1}{3}n(Fe^{2+}){totale}-n(Fe^{2+}){excès}$$
$$n\left(NO_3^-\right)=\frac{1}{3}\left[4,0\times 10^{-3}-3,6\times 10^{-3}\right]$$
$$n\left(NO_3^-\right)=1,3\times 10^{-4}\ mol$$
$$t_2=\frac{m\left(NO_3^-\right)}{V}$$
$$t_2=\frac{n\left(NO_3^-\right)\times M\left(NO_3^-\right)}{V}$$
$$t_2=\frac{1,3\times 10^{-4}\times 62,0}{250\times 10^{-3}}$$
$$t_2=0,032\ g.L^{-1}$$
$$t_2=32\ mg.L^{-1}$$
La concentration en masse en ion nitrate t2 vaut environ 33 mg·L-1.
L’incertitude-type u(t2) sur la valeur de la concentration t2 de nitrates déterminée avec le titrage est donnée par la relation :
$$ u(t_2)=t_2 \times \sqrt{\left(\frac{u(C)}{C}\right)^2+\left(\frac{u(V_E)}{V_E}\right)^2+\left(\frac{u(V)}{V}\right)^2} $$
avec :
- u(VE) = 0,5 mL, incertitude-type sur la valeur du volume VE de solution titrante versée à l’équivalence.
- u(V), incertitude-type sur la valeur du volume de solution titrée V.
- u(C), incertitude-type sur la valeur de la concentration en quantité de matière [Cr2O72-] = C en ions dichromate Cr2O72-.
8. Calculer l’incertitude-type u(t2) de la teneur en ions nitrate puis donner un encadrement de la concentration en masse t2 obtenue avec cette méthode de titrage.
$$u\left(t_2\right)=t_2\times \sqrt{\left(\frac{u(C)}{C}\right)^2+\left(\frac{u\left(V_E\right)}{V_E}\right)^2+\left(\frac{u\left(V\right)}{V}\right)^2}$$
$$u\left(t_2\right)=32\ \times \sqrt{\left(\frac{0,2\times {10}^{-2}}{5,0\times {10}^{-2}}\right)^2+\left(\frac{0,5}{12}\right)^2+\left(\frac{0,2}{250}\right)^2}$$
$$u\left(t_2\right)=2\ mg{.L}^{-1}$$
$$t_2=32\pm 2\ mg{.L}^{-1}$$
$$30\ mg{.L}^{-1}<t_2<34\ mg{.L}^{-1}$$
9. Conclure sur la potabilité de l’eau prélevée au regard des résultats obtenus par les deux méthodes de dosage étudiées.
D’après l’énoncé : « L’Organisation Mondiale de la Santé (OMS) a fixé la concentration maximale en ions nitrate dans l’eau à 50 mg·L-1. »
t1 et t2 sont inferieurs à la concentration maximale donc l’eau prélevée est potable au regard des résultats obtenus par les deux méthodes de dosage étudiées.
Partie C – Combien de temps peut-on conserver un biberon préparé avec du lait en poudre ?
On prépare un biberon par dissolution de lait en poudre dans de l’eau.
Un lait présente une légère acidité qui peut se développer assez vite selon les conditions de conservation. En effet, le lactose présent dans le lait se transforme progressivement en acide lactique.
On vérifie l’état de conservation d’un lait en mesurant son acidité exprimée en degré Dornic (°D). Un degré Dornic, noté 1°D, correspond à 0,10 g d’acide lactique par litre de lait.
Données
- Formule semi-développée de l’acide lactique :
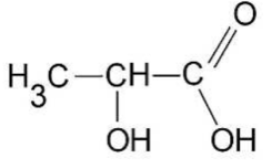
- Masse molaire de l’acide lactique : M = 90,0 g·mol-1
- pKa (acide lactique/ion lactate) = 3,9
- Couples acide/base de l’eau : H3O+(aq)/H2O(ℓ) H2O(ℓ)/HO–(aq)
- Rappel : pKa = – log Ka
Le couple acide lactique / ion lactate
10. Recopier la formule semi-développée de l’acide lactique, entourer les groupes caractéristiques et indiquer leur nom.
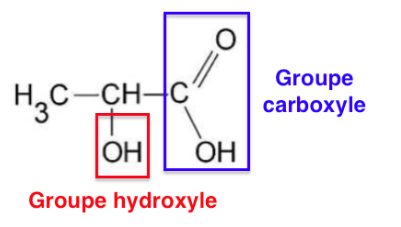
11. Représenter le schéma de Lewis de l’ion lactate, base conjuguée de l’acide lactique.
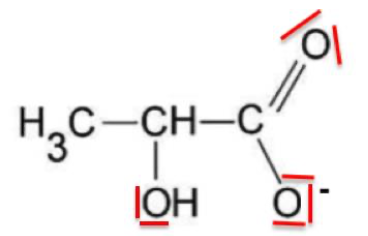
Pour la suite, on note AH l’acide lactique et A– sa base conjuguée. La réaction chimique entre l’acide lactique AH et l’eau du biberon conduit à un équilibre chimique :
AH(aq) + H2O(ℓ) ⇌ A–(aq) + H3O+(aq)
La mesure au laboratoire du pH du lait contenu dans le biberon indique un pH = 6,2.
12. Après avoir représenté le diagramme de prédominance du couple AH/A–, indiquer quelle espèce prédomine dans le lait du biberon.
Diagramme de prédominance :

pH = 6,2 pour le lait contenu dans le biberon : $A^-$ prédomine dans le lait du biberon.
13. Exprimer la constante d’acidité 𝐾𝐴 du couple AH/A– en fonction des concentrations [AH], [A–], [H3O+] et c° avec c° = 1 mol·L-1, concentration standard.
$$K_a=\frac{\left[A^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[HA\right]_{eq}\times c^0}$$
14. En déduire que la concentration en ion lactate [A–] dans le lait du biberon est environ 200 fois supérieure à celle en acide lactique [AH].
$$\frac{\left[A^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[HA\right]{eq}\times c^0}=K_a$$
$$\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}=K_a\times\frac{c^0}{\left[H_3O^+\right]{eq}}$$
$$\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}=10^{-pK_a}\times\frac{c^0}{c^0\times10^{-pH}}$$
$$\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}=10^{-pK_a+pH}$$
$$\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}=10^{-3,9+6,2}=200$$
$$\left[A^-\right]{eq}=200\left[HA\right]{eq}$$
Dosage de l’acide lactique
Afin de déterminer la concentration en acide lactique dans le lait, on met en œuvre le protocole suivant :
- Verser dans un erlenmeyer VL = 40,0 mL de lait.
- Ajouter Veau = 150 mL d’eau distillée.
- Ajouter quelques gouttes d’indicateur coloré (qui permettront de repérer l’équivalence).
- Placer l’erlenmeyer sous une burette remplie de solution d’hydroxyde de sodium (Na+, HO–) de concentration cB = 2,0·10-2 mol·L-1 et agiter.
- Verser jusqu’au changement de couleur et noter le volume de soude versé VBE.
Pour un même échantillon de lait, on recommence la manipulation plusieurs fois. Les valeurs de VBE ainsi obtenues sont regroupées dans le tableau ci-dessous.
| VBE (mL) | 12,3 | 12,2 | 12,4 | 12,0 | 12,1 | 12,2 |
La valeur moyenne de ces valeurs est $\overline{V_{BE}}=12,2\ \text{mL}$.
Au cours de la transformation, les couples acide-base mis en jeu sont : AH/A– et H2O/HO–.
15. Écrire la réaction support du dosage.
Équation de la réaction support du titrage :
$$AH_{(aq)}+{\rm HO}{(aq)}^-\rightarrow A{(aq)}^-+H_2O_{(l)}$$
16. Déterminer la concentration en masse d’acide lactique dans le lait de biberon.
A l’équivalence :
$$\frac{n_{AH}^i}{1}=\frac{n_{HO^-}^{eq}}{1}$$
$$\frac{m_{AH}}{M_{AH}}=C_B\times V_{BE}$$
$$m_{AH}=C_B\times V_{BE}\times M_{AH}$$
Or
$$c_m=\frac{m_{AH}}{V_L}$$
$$m_{AH}=c_m\times V_L$$
D’ou
$$c_m\times V_L=C_B\times V_{BE}\times M_{AH}$$
$$c_m=\frac{C_B\times V_{BE}\times M_{AH}}{V_L}$$
$$c_m=\frac{2,0\times {10}^{-2}\times 12,2\times {10}^{-3}\times 90,0}{40,0\times {10}^{-3}}$$
$$c_m=0,55\ g{.L}^{-1}$$
La dispersion des mesures de VBE peut s’expliquer par des imprécisions sur les valeurs de certains paramètres.
17. Parmi les deux paramètres suivants, volume de lait, VL, et volume d’eau distillée, Veau, indiquer lequel a une incidence sur la valeur de VBE.
$V_L$ a une incidence sur $V_{BE}$.
L’eau ajouté n’entraine pas une réaction avec ${\rm HO}_{(aq)}^-$.
D’après la question précédente :
$$c_m=\frac{C_B\times V_{BE}\times M_{AH}}{V_L}$$
$$\frac{C_B\times V_{BE}\times M_{AH}}{V_L}=c_m$$
$$V_{BE}=\frac{c_m\times V_L}{C_B\times V_{BE}\times M_{AH}}$$
$V_{BE}$ dépend de $V_L$ mais de dépend pas de $V_{eau}$.
Suivi temporel de la concentration en acide lactique dans plusieurs échantillons
Des tests ont été effectués sur trois échantillons provenant du lait d’un biberon classique préparé par dissolution de lait en poudre dans de l’eau. Ces échantillons ont ensuite été stockés pendant plusieurs jours aux températures suivantes :
- Echantillon 1 : 5 °C.
- Echantillon 2 : 20 °C.
- Echantillon 3 : 30 °C.
Un suivi par titrage a permis de déterminer la concentration en masse d’acide lactique dans chaque échantillon en fonction du temps. Les résultats obtenus sont présentés ci-dessous (figure 3). Chaque courbe correspond à l’un des échantillons étudiés.
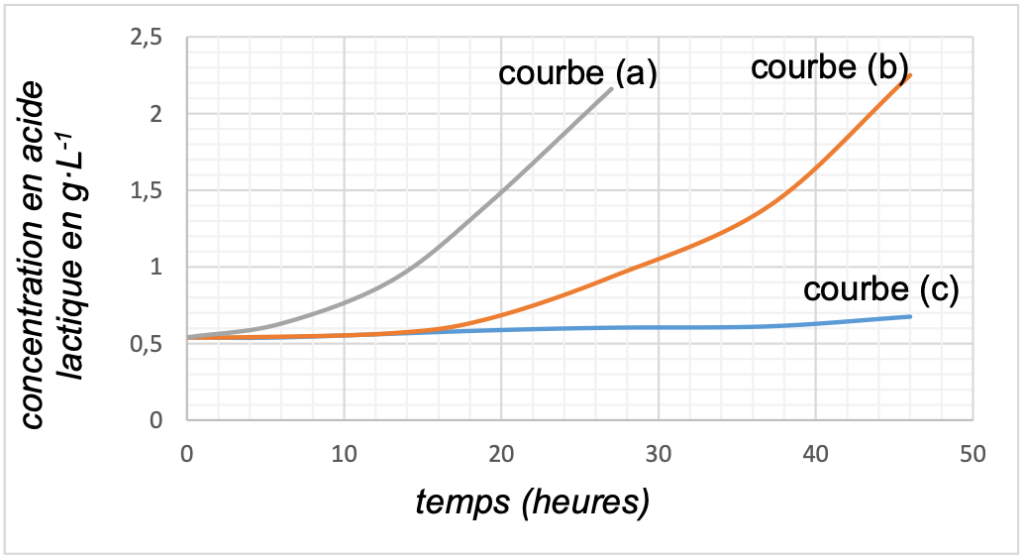
Figure 3. Suivi cinétique de la formation d’acide lactique pour trois températures
Un lait est considéré comme frais, selon les normes en vigueur, si son acidité est inférieure à 18°D.
18. À l’aide du graphe de la figure 3, déterminer au bout de combien de temps les échantillons 2 et 3 ne sont plus considérés comme étant des laits frais.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
t_1<t_2<t_3 or la température est un facteur cinétique : plus la température est élevée, plus la concentration en acide lactique augmente rapidement.
t_1 : courbe c
t_2 : courbe b
t_3 : courbe a
| 1°D | $0,1\ g{.L}^{-1}$ |
| 18°D | x |
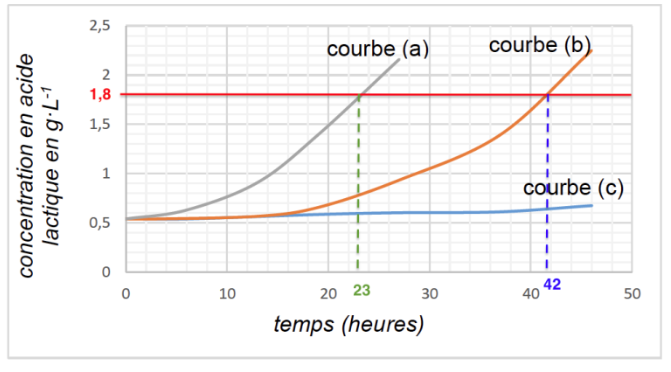
$$x=\frac{18\times 0,1}{1}=1,8\ g{.L}^{-1}$$ d’acide lactique
L’échantillon 2 (courbe b) n’est plus considéré comme étant un lait frais au bout de 42 heures.
L’échantillon 3 (courbe a) n’est plus considéré comme étant un lait frais au bout de 23 heures.
