Bac Centres étrangers 2023 Sujet 2
Exercice 2 – (4,5 points) – Durée 0h47 – Calculatrice autorisée
Sujet n°23-PYCJ2G11
Sujet et corrigé
EXERCICE 2 – L’ÉRYTHROSINE, COLORANT ALIMENTAIRE (4,5 points)
L’érythrosine est un colorant synthétique rouge contenant de l’iode. Très soluble dans l’eau, ce colorant est utilisé pour colorer les aliments, notamment les cerises en conserve, ainsi que pour teinter des préparations microscopiques ou des médicaments. Les taches dues à ce colorant peuvent être traitées à l’eau de Javel.
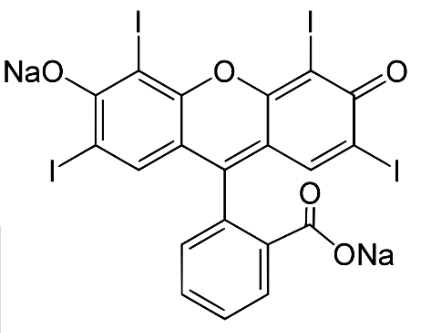
Document
La DJA (Dose Journalière Admissible qu’un individu peut ingérer sans risque pour sa santé) est de 0,1 mg/kg de masse corporelle, par jour.
Extrait de : https://www.avenir-bio.fr/additif,E127
Dans la partie A, on souhaite savoir si une solution d’érythrosine contenue dans une boîte de conserve de cerises respecte la DJA. La seule espèce colorée dans cette solution est l’érythrosine.
Dans la partie B, on s’intéresse à la cinétique de la décoloration de l’érythrosine par l’eau de Javel.
Données
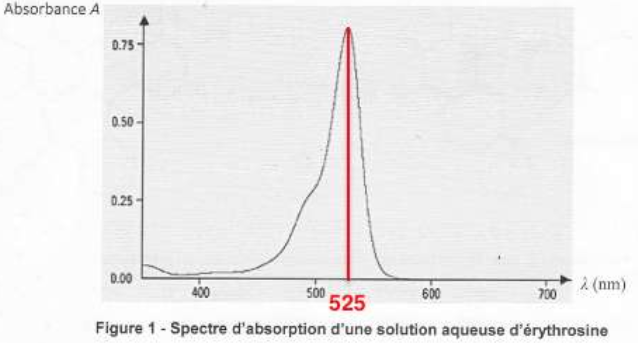
– Spectre d’absorption d’une solution aqueuse d’érythrosine de référence.
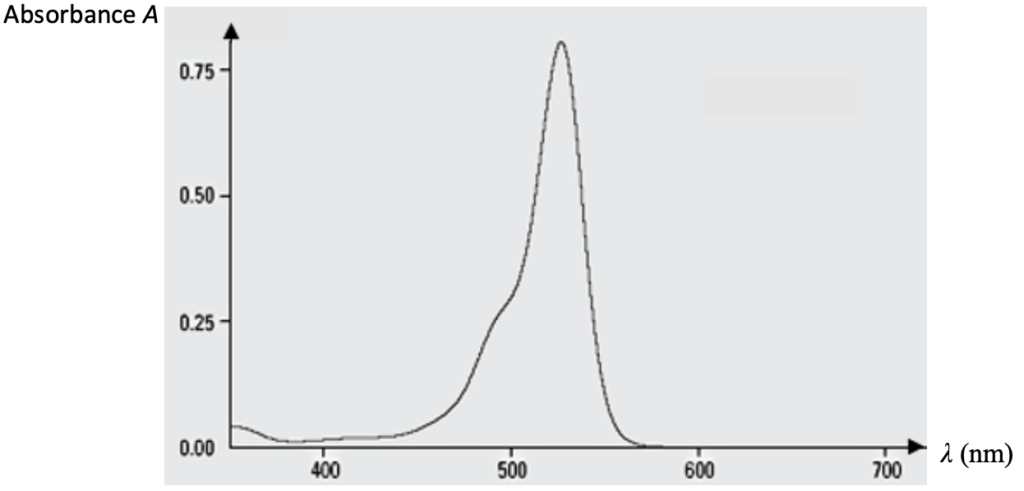
Figure 1 – Spectre d’absorption d’une solution aqueuse d’érythrosine
- Volume de la solution d’érythrosine extraite de la boîte de conserve de cerises : V = 500 mL
- Coefficient d’absorption molaire de l’érythrosine dans les conditions de l’expérience :
𝜀 = 8,2 × 104 L∙mol-1∙cm-1
- Longueur de la cuve du spectrophotomètre : 𝑙 = 1,0 cm
- Rappel de la loi de Beer-Lambert : 𝐴 = 𝜀 × 𝑙 × 𝑐
- Masse volumique de l’eau de Javel utilisée : 𝜌𝐽 = 1095 g ∙ L−1
- Masse molaire de l’érythrosine : ME = 879,86 g∙mol-1
- Autres masses molaires : M(Cl) = 35,5 g·mol-1 ; M(O) = 16,0 g·mol-1.
On note [E] la concentration en quantité de matière d’érythrosine dans la solution.
Partie A – Concentration en érythrosine dans la solution contenue dans la boîte de cerises
1. Proposer une valeur de la longueur d’onde 𝜆𝑚 à laquelle régler le spectrophotomètre.
On choisi la longueur d’onde au pic de l’absorbance :
$\lambda_m=525\ nm$
2. À partir de la loi de Beer-Lambert, montrer que la mesure de l’absorbance de la solution étudiée permet de déterminer la concentration en érythrosine.
Loi de Beer-Lambert :
$A=\epsilon\times l\times c$
$c=\frac{A}{\epsilon\times l}$
Ainsi la mesure de l’absorbance de la solution étudiée permet de déterminer la concentration en érythrosine à partir de la loi de Beer-Lambert.
On mesure l’absorbance de la solution étudiée. La valeur obtenue est Asolution = 0,44.
3. Montrer que la concentration de la solution en érythrosine est : [𝐸] = 5,4 × 10−6 mol · L−1.
$c=\frac{A}{\epsilon\times l}$
$\left[E\right]=\frac{A_{solution}}{\epsilon\times l}$
$\left[E\right]=\frac{0,44}{8,2\times{10}^4\times1,0}$
$\left[E\right]=5,4\times{10}^{-6}\ mol.L^{-1}$
4. En s’appuyant sur la valeur de la DJA citée dans le document de l’introduction, montrer qu’une personne de 50 kg peut consommer la totalité de la solution contenue dans la conserve de cerises sans risque pour sa santé.
DJA : 0,1 mg/kg
Une personne de 50kg peut consommer $50\times0,1\times{10}^{-3}=5,0\times{10}^{-3}g$
Calculons la masse contenue dans la solution :
$m=n\times M$
Or $n=\left[E\right]\times V$
D’ou
$m=\left[E\right]\times V\times M$
$m=5,4\times{10}^{-6}\times500\times{10}^{-3}\times878,86$
$m=2,4\times{10}^{-3}g$
La masse contenue dans la solution est inférieure à la masse maximale qu’une personne de 50kg peut consommer. Ainsi, une personne de 50kg peut consommer la totalité de la solution contenue dans la conserve de cerises sans risque pour sa santé.
Partie B – Cinétique de la décoloration de l’érythrosine par l’eau de Javel
En cas de taches, l’érythrosine peut être décolorée par les ions hypochlorite ClO− apportés par une solution d’eau de Javel. Un composé incolore se forme selon l’équation :
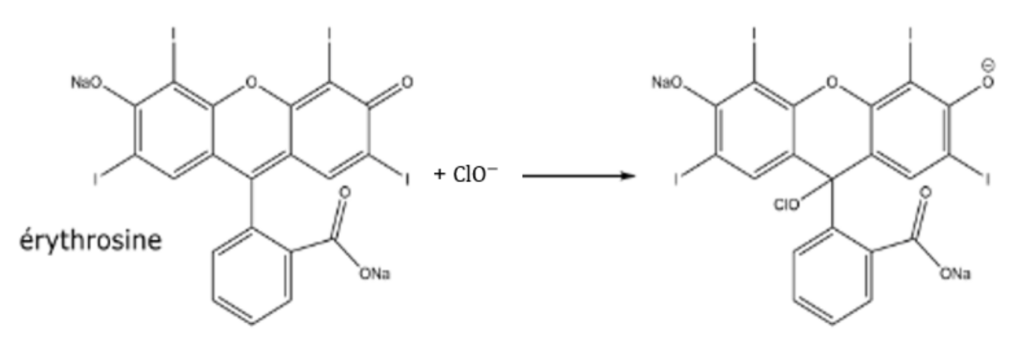
Avec les notations E pour l’érythrosine et P pour le composé formé, on peut écrire :
E(aq) + ClO−(aq) → P(aq) (équation 1)
rouge incolore incolore
On s’intéresse à la rapidité avec laquelle l’eau de Javel permet d’effacer les taches d’érythrosine, dans le cas où l’ion hypochlorite est en excès.
Protocole
Pour préparer la solution en ions hypochlorite ClO−, on utilise une solution commerciale S0 d’eau de Javel contenant 4,8 % en masse d’ion hypochlorite.
On prélève V0 = 30 mL de solution S0 que l’on verse dans une fiole jaugée de volume Vj = 100 mL et on complète jusqu’au trait de jauge. On obtient ainsi une solution S1 de volume Vj = 100 mL.
À la date t = 0 s, on mélange V1 = 5 mL de solution S1 avec VE = 5 mL de solution d’érythrosine dont la concentration en érythrosine a été déterminée à la question 3 et on mesure l’absorbance du mélange au cours du temps, voir figure 2 ci-dessous.
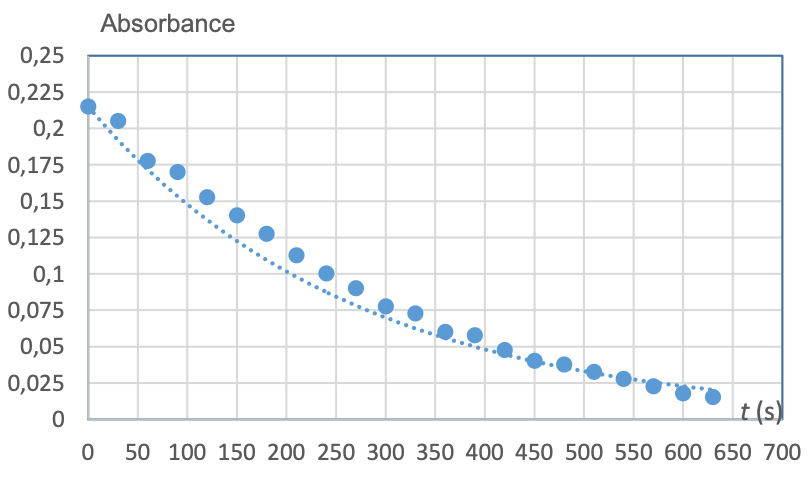
Sur cette figure, on a superposé une modélisation, en pointillés, aux points expérimentaux. L’équation de la courbe de modélisation est donnée par le tableur :
𝐴 = 0,215 e−0,0036 𝑡
Figure 2 – Évolution temporelle de l’absorbance de la solution d’érythrosine
5. Montrer que la concentration de la solution S1 en ion hypochlorite ClO− est C1 = 3,1×10-1 mol·L-1.
$C=\frac{n_{{\rm ClO}^-}}{V_{Solution}}$
Or
$n_{{\rm ClO}^-}=\frac{m_{{\rm ClO}^-}}{M_{{\rm ClO}^-}}$
Ainsi :
$C=\frac{n_{{\rm ClO}^-}}{V_{Solution}}=\frac{m_{{\rm ClO}^-}}{M_{{\rm ClO}^-}\times V_{Solution}}$
Or le pourcentage est défini par :
$w=\frac{m_{{\rm ClO}^-}}{m_{solution}}$
D’ou
$m_{{\rm ClO}^-}=w\times m_{solution}$
Ainsi :
$C=\frac{m_{{\rm ClO}^-}}{M_{{\rm ClO}^-}\times V_{Solution}}=\frac{w\times m_{solution}}{M_{{\rm ClO}^-}\times V_{Solution}}$
Or
$\rho_{solution}=\frac{m_{solution}}{V_{Solution}}$
Ainsi :
$C=\frac{w\times m_{solution}}{M_{{\rm ClO}^-}\times V_{Solution}}=\frac{w\times\rho_{solution}}{M_{{\rm ClO}^-}}$
$C=\frac{\frac{4,8}{100}\times1095}{35,5+16,0}$
$C=1,0\ mol.L^{-1}$
Lors d’une dilution la quantité de matière se conserve :
$n_1=n_0$
$c_1\times V_j=c\times V_0$
$c_1=\frac{c\times V_0}{V_j}$
$c_1=\frac{1,0\times30\times{10}^{-3}}{100\times{10}^{-3}}$
$c_1=3,0\times{10}^{-1}mol.L^{-1}$
6. En calculant les quantités de matière initiales en érythrosine nEi et en ion hypochlorite nHi, montrer que les ions hypochlorite sont effectivement en excès.
$n_{Hi}=c_1\times V_1$
$n_{Hi}=3,0\times{10}^{-1}\times5\times{10}^{-3}$
$n_{Hi}=1,5\times{10}^{-3}\ mol$
$n_{Ei}=\left[E\right]\times V_E$
$n_{Ei}=5,4\times{10}^{-6}\times5\times{10}^{-3}$
$n_{Ei}=2,7\times{10}^{-8}\ mol$
$E(aq)+{\rm ClO}^-(aq)\rightarrow P(aq)$
$\frac{n_{Ei}}{1}<\frac{n_{Hi}}{1}$
Ainsi, les ions hypochlorite sont en excès.
7. Définir la vitesse volumique de disparition 𝑣 de l’érythrosine en utilisant la notation [E].
$v=-\frac{d\left[E\right]}{dt}$
8. Donner l’expression de la vitesse volumique de disparition 𝑣 de l’érythrosine en fonction de la concentration [E] et d’une constante 𝑘 positive dans le cas où la loi de vitesse est d’ordre 1.
Dans le cas d’une loi de vitesse d’ordre 1, la relation existant entre la vitesse volumique de disparition $v$ de l’érythrosine, la concentration $\left[E\right]$ et une constante positive $k$ est :
$v=k\times c$
Dans le cas où la loi de vitesse est d’ordre 1, l’équation différentielle satisfaite par la concentration [E] est donc : $\frac{d[E]}{dt}+k \times [E]=0$. Les solutions de cette équation différentielle sont de la forme :
[E](𝑡) = [E]0 e−𝑘𝑡
Par ailleurs, on rappelle que, pour la fonction logarithme népérien, on a les relations :
ln(𝑎 × 𝑏) = ln(𝑎) + ln(𝑏) et ln e𝑥 = 𝑥
9. Montrer que le temps de demi-réaction 𝑡1/2 pour une loi de vitesse d’ordre 1 est donné par la relation : $t_{1/2}=\frac{\ln(2)}{k}$
$t_{1/2}$ est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale :
$x(t_{1/2})=\frac{x_f}{2}$
on a donc :
$\left[E\right]{\left(t=t{1/2}\right)}=\frac{\left[E\right]_0}{2}$
Or
$\left[E\right]{\left(t=t{1/2}\right)}=\left[E\right]0{\times e}^{-k\times t{1/2}}$
Donc
$\left[E\right]0{\times e}^{-k\times t{1/2}}=\frac{\left[E\right]0}{2}$
$e^{-k\times t{1/2}}=\frac{1}{2}$
$\ln\left(e^{-k\times t_{1/2}}\right)=\ln\left(\frac{1}{2}\right)$
$-k\times t_{1/2}=-\ln\left(2\right)$
$t_{1/2}=\frac{\ln\left(2\right)}{k}$
10. Montrer, en utilisant le résultat de la question 2, que si la décoloration de l’érythrosine suit une loi de vitesse d’ordre 1, alors l’évolution de l’absorbance en fonction du temps est une exponentielle.
D’après l’énoncé : dans le cas ou la loi de vitesse est d’ordre 1, les solutions de cette équation différentielle sont de la forme :
$\left[E\right]=\left[E\right]_0{\times e}^{-k\times t}$
Or Loi de Beer-Lambert (question2):
$A=\epsilon\times l\times c$
$A=\epsilon\times l\times\left[E\right]$
$\left[E\right]=\frac{A}{\epsilon\times l}$
On a donc :
$\frac{A}{\epsilon\times l}=\left[E\right]_0{\times e}^{-k\times t}$
$A=\epsilon\times l\times\left[E\right]_0{\times e}^{-k\times t}$
Ainsi, l’évolution de l’absorbance en fonction du temps est une exponentielle.
11. Déterminer la valeur de 𝑡1/2 en indiquant la méthode utilisée et conclure sur la rapidité de l’action de l’eau de Javel sur l’érythrosine.
L’équation de la courbe de modélisation donnée par le tableau est :
$A=0,215{\times e}^{-0,0036\times t}$
Or
$A=\epsilon\times l\times\left[E\right]_0{\times e}^{-k\times t}$
Par identification
$k=0,0036\ s^{-1}$
D’après la question 9 :
$t_{1/2}=\frac{\ln\left(2\right)}{k}$
$t_{1/2}=\frac{\ln\left(2\right)}{0,0036}$
$t_{1/2}=193\ s$
$t_{1/2}=3\ min\ 13\ s$
L’action de l’eau de Javel sur l’érythrosine est lente.
