L’acétanilide, médicament antipyrétique

Bac Centres étrangers 2023 Sujet 2

Exercice 3 – (4,5 points) – Durée 0h47 – Calculatrice autorisée

Sujet n°23-PYCJ2G11

Sujet et corrigé

Télécharger le sujet complet en PDF :

EXERCICE 3 – L’ACÉTANILIDE, MÉDICAMENT ANTIPYRÉTIQUE (4,5 points)

L’acétanilide est un composé organique, solide, blanc, obtenu par l’action de l’anhydride éthanoïque (CH₃CO)₂O sur l’aniline C₆H₅NH₂, et utilisé en pharmacologie. Sa formule semi-développée est donnée figure 1 ci-dessous.

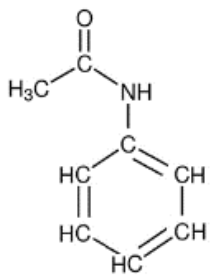
Figure 1 – Formule semi-développée de l’acétanilide

Cette molécule est obtenue selon la réaction d’équation :

(CH₃CO)₂O + C₆H₅NH₂ CH₃-CO-NH-C₆H₅ + CH₃CO₂H (équation 1)

Le but de l’exercice est d’étudier trois protocoles expérimentaux afin de déterminer les conditions optimales d’obtention de l’acétanilide CH₃-CO-NH-C₆H₅.

Pour simplifier, les différents composés sont notés par des lettres :

A = (CH₃CO)₂O    anhydride éthanoïque
B = C₆H₅NH₂             aniline
C = CH₃-CO-NH-C₆H₅       acétanilide
D = CH₃CO₂H                 acide éthanoïque

Données

Masse volumique de l’anhydride éthanoïque : ρ_A = 1,08 g·mL^-1
Masse molaire de l’anhydride éthanoïque : M_A = 102,09 g·mol^-1
Masse volumique de l’aniline : ρ_B = 1,02 g·mL^-1
Masse molaire de l’aniline : M_B = 93,13 g·mol^-1
Masse molaire de l’acétanilide : M_C = 135,17 g·mol^-1
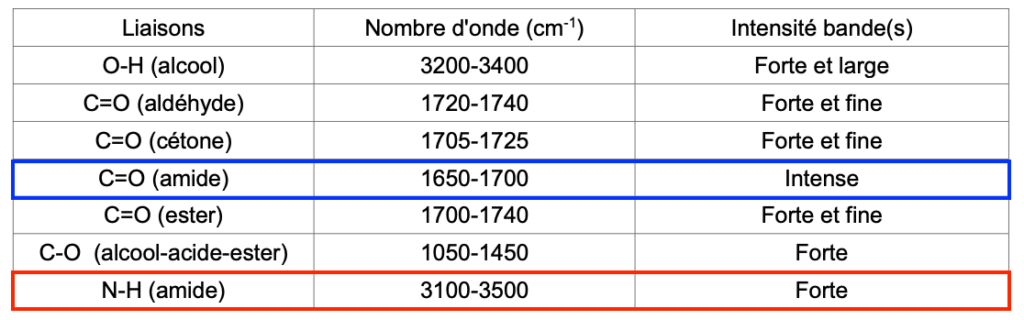
Nombres d’onde et allure des bandes d’absorption de quelques liaisons :

Liaisons	Nombre d’onde (cm^-1)	Intensité bande(s)
O-H (alcool)	3200-3400	Forte et large
C=O (aldéhyde)	1720-1740	Forte et fine
C=O (cétone)	1705-1725	Forte et fine
C=O (amide)	1650-1700	Intense
C=O (ester)	1700-1740	Forte et fine
C-O (alcool-acide-ester)	1050-1450	Forte
N-H (amide)	3100-3500	Forte

La molécule d’acétanilide

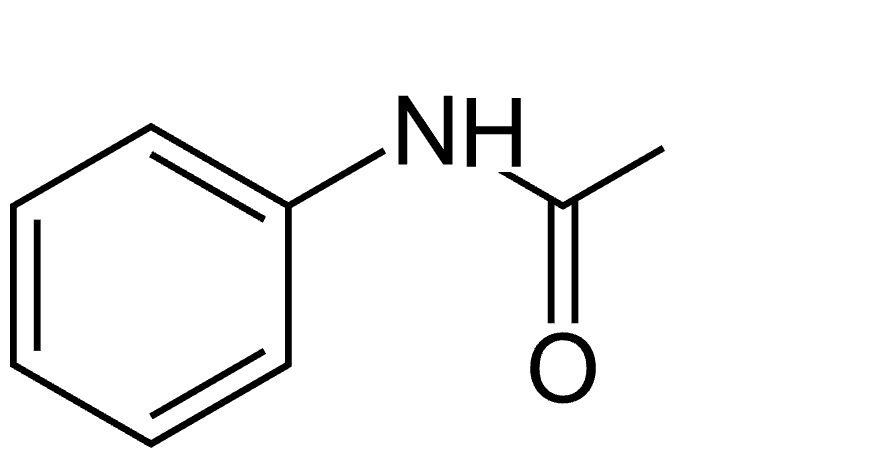
1. Représenter la formule topologique de l’acétanilide. Identifier la famille fonctionnelle à laquelle l’acétanilide appartient parmi les suivantes : alcool, aldéhyde, cétone, amide, ester.

L’acétanilide appartient à la famille des amides

2. Montrer que le spectre infrarouge de l’acétanilide (figure 2 ci-dessous) permet de confirmer que l’acétanilide appartient bien à cette famille fonctionnelle.

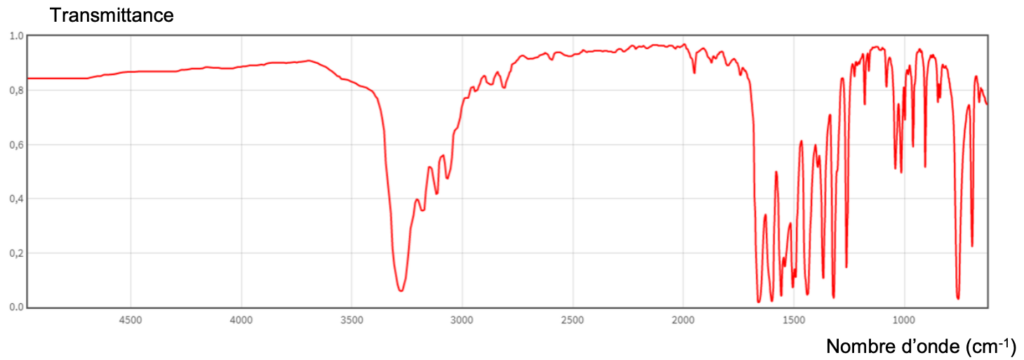
Figure 2 – Spectre infrarouge de l’acétanilide

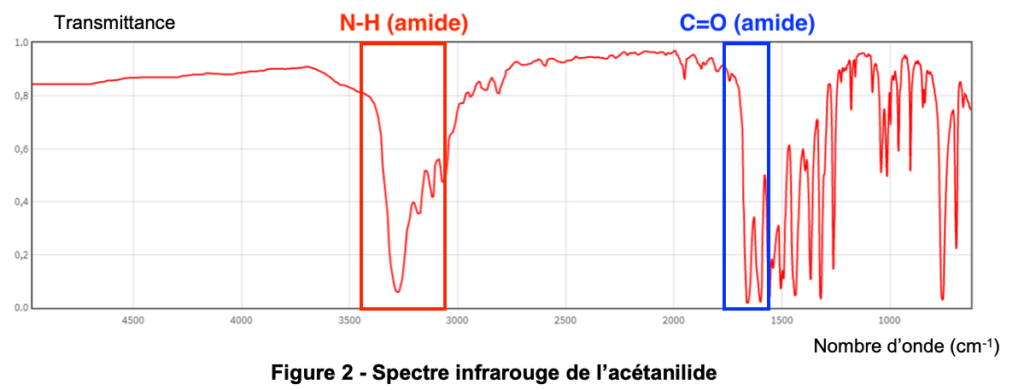
Le spectre infrarouge de l’acétanilide comporte des bandes d’absorption correspondant aux liaisons :
N-H (amide)
C=O (amide)

Ainsi, le spectre infrarouge de l’acétanilide permet de confirmer que l’acétanilide appartient bien à la famille fonctionnelle des amides.

Protocoles expérimentaux

On met en œuvre trois protocoles expérimentaux différents, présentés figure 3 ci-dessous, afin d’étudier les conditions optimales de synthèse de l’acétanilide.

Les réactifs sont introduits dans un ballon adapté aux montages des protocoles 1, 2 ou 3.

Après une vingtaine de minutes, le mélange est refroidi dans un bain d’eau glacée afin de faire précipiter le produit C obtenu.

On filtre ensuite le mélange, on le rince à l’eau distillée, puis les cristaux obtenus sont séchés à l’étuve. On pèse ensuite le produit C.

Numéro du protocole	1	2	3
Montage utilisé	Chauffage à reflux	Chauffage à reflux adapté d’un montage DEAN-STARK*	Chauffage à reflux
Volume du réactif A (mL) (CH3CO)2O	15,0	15,0	30,0
Volume du réactif B (mL) C6H5NH2	14,5	14,5	14,5
Masse mC du produit C (g) CH3-CO-NH-C6H5	10,7	21,4	14,3
Rendement r		1,0	0,67

Figure 3 – Récapitulatif des différents protocoles

(*) Un montage DEAN-STARK est un montage qui permet d’éliminer un produit au cours de sa formation.

Etude du protocole 1

3. Montrer que, dans le cas du protocole 1, les réactifs sont introduits dans le ballon en proportions stœchiométriques.

$n=\frac{m}{M}$
Or
$\rho=\frac{m}{V}$
$m=\rho\times V$
$n=\frac{\rho\times V}{M}$

$n_A=\frac{\rho_A\times V_A}{M_A}$
$n_A=\frac{1,08\times15,0}{102,09}$
$n_A=1,59{\times10}^{-1}\ mol$

$n_B=\frac{\rho_B\times V_B}{M_B}$
$n_B=\frac{1,02\times14,5}{93,13}$
$n_B=1,59{\times10}^{-1}\ mol$

$\frac{n_A}{1}=\frac{n_B}{1}\ $ :
Les réactifs sont introduits dans le ballon en proportion stoechiométrique.

La constante d’équilibre K associée à l’équation 1 a pour valeur K = 1,0 à la température de l’expérience.

Par ailleurs, on admet que, dans les conditions de l’expérience, le quotient de réaction 𝑄𝑅(𝑥) s’écrit, pour un avancement x donné :

$$Q_R(x)=\frac{n(C)\times n(D)}{n(A)\times n(B)}$$

𝑛(X) désigne la quantité de matière (en mol) de l’espèce X.

4. Donner la valeur du quotient de réaction initial, Q_R (𝑥 = 0), pour le protocole 1.

$Q_R(x)=\frac{n\left(C\right)\times n\left(D\right)}{n\left(A\right)\times n\left(B\right)}$
$Q_R(x=0)=\frac{0\times0}{1,59{\times10}^{-1}\times1,59{\times10}^{-1}}$
$Q_R(x=0)=0$

5. En déduire le sens d’évolution spontanée de la réaction chimique d’équation 1.

$K=1,0$
$Q_R\left(x=0\right)=0<K$
Ainsi, le sens d’évolution spontanée de la réaction chimique d’équation 1 est le sens direct.

6. Recopier et compléter le tableau d’avancement de la réaction de formation de l’acétanilide.

	Avancement x	(CH₃CO)₂O + C₆H₅NH₂ CH₃-CO-NH-C₆H₅ + CH₃CO₂H
État initial	x = 0	n(A)i	n(B)i	0	0
État final	x_f

	Avancement x	(CH₃CO)₂O + C₆H₅NH₂ CH₃-CO-NH-C₆H₅ + CH₃CO₂H
État initial	x = 0	n(A)i	n(B)i	0	0
État final	x_f	${n\left(A\right)}_i-x_f$	${n\left(B\right)}_i-x_f$	$x_f$	$x_f$

7. Déterminer la masse maximale théorique m_max de produit C qui serait obtenue si la réaction était totale pour le protocole 1.

${n\left(A\right)}i-x{max1}=0$
$x_{max1}={n\left(A\right)}i$
$x{max1}=1,59{\times10}^{-1}\ mol$

${n\left(B\right)}i-x{max2}=0$
$x_{max2}={n\left(B\right)}i$
$x{max2}=1,59{\times10}^{-1}\ mol$

$x_{max}=1,59{\times10}^{-1}\ mol$

Calculons la masse maximale de produit C qui peut être obtenue :
$n_C^{maximale}=\frac{m_C^{maximale}}{M_C}$
$m_C^{maximale}=n_C^{maximale}\times M_C$
$m_C^{maximale}=x_{max}\times M_C$
$m_C^{maximale}=1,59{\times10}^{-1}\times135,17$
$m_C^{maximale}=21,5\ g$

8. Exprimer le rendement r de la réaction pour le protocole 1 en fonction de m_C (voir figure 3) et de m_max. Calculer sa valeur.

$\eta=\frac{m_C^{experimentale}}{m_C^{maximale}}$
$\eta=\frac{10,7}{21,5\ }$
$\eta=0,498$

9. Exprimer le quotient de réaction 𝑄_𝑅(𝑥 = 𝑥_𝑓) à l’état final pour le protocole 1 en fonction de l’avancement final 𝑥_𝑓.

$Q_R(x=x_f)=\frac{{n\left(C\right)}_f\times{n\left(D\right)}_f}{{n\left(A\right)}_f\times{n\left(B\right)}_f}$
$Q_R(x=x_f)=\frac{x_f\times x_f}{\left({n\left(A\right)}_i-x_f\right)\times\left({n\left(B\right)}_i-x_f\right)}$

10. Calculer la valeur de 𝑄_𝑅(𝑥 = 𝑥_𝑓) et, à partir de cette valeur, indiquer si l’état d’équilibre est atteint.

Trouvons $x_f$ :
$x_f=n_C^f=\frac{m_C^f}{M_C}$
$x_f=\frac{m_C^f}{M_C}$
$x_f=\frac{10,7}{135,17}$
$x_f=7,92{\times10}^{-2}\ mol$

$Q_R(x=x_f)=\frac{x_f\times x_f}{\left({n\left(A\right)}_i-x_f\right)\times\left({n\left(B\right)}_i-x_f\right)}$
$Q_R(x=x_f)=\frac{7,92{\times10}^{-2}\times7,92{\times10}^{-2}}{\left(1,59{\times10}^{-1}-7,92{\times10}^{-2}\right)\times\left(1,59{\times10}^{-1}-7,92{\times10}^{-2}\right)}$
$Q_R(x=x_f)=0,985$

$Q_R(x=x_f)\approx K$
L’état d’équilibre est atteint.

Les protocoles 2 et 3

11. Expliquer pourquoi la mise en œuvre des protocoles 2 et 3 permet d’optimiser le rendement.

Le protocole 2 utilise un montage de DEAN-STARK qui permet d’éliminer un produit au cours de sa formation. Ainsi, la quantité de matière d’un des produits est nulle (n(C)=0 ou n(D)=0) et donc
$Q_R\left(x\right)=\frac{n\left(C\right)\times n\left(D\right)}{n\left(A\right)\times n\left(B\right)}=0$
$Q_R\left(x\right)$ sera donc toujours inferieur à $K$ et donc la réaction se déroulera dans le sens direct jusqu’à épuisement des réactifs : la réaction sera totale.

Le protocole 3 utilise un volume du réactif A supérieur au protocole 1. Ainsi, pour atteindre l’équilibre $Q_R\left(x=x_f\right)=K$ il faut une quantité de matière des produits plus importante car $Q_R$ est inversement proportionnel à $n(A)$.
La quantité de matière des produits plus importante, le rendement est supérieure au rendement de la réaction 1.

Bilan

12. Indiquer le protocole le plus intéressant parmi les trois en justifiant.

Le protocole le plus intéressant est le protocole 2 car le rendement est maximal et on garde des proportions steochiometriques.

Télécharger l’exercice en PDF :

Télécharger le sujet complet en PDF :