Bac La Réunion 2023 Sujet 2
Exercice 3 – (4 points) – Durée 0h42 – Calculatrice autorisée
Sujet n°23-PYCJ2LR1
Sujet et corrigé
EXERCICE III : ANALYSE D’UN SOL (4 points)
De nombreux éléments minéraux, tel le fer, et l’azote sont indispensables pour permettre aux végétaux de synthétiser la chlorophylle. Si ces éléments sont déficitaires dans le sol, la concentration en chlorophylle sera moindre et la couleur des végétaux moins verte. Ainsi, lorsqu’un sol est en carence de fer, les feuilles se décolorent et deviennent jaunes : c’est ce qu’on appelle la chlorose ferrique.
PARTIE A : Étude de la réaction mise en jeu
En présence d’ions thiocyanate SCN−(aq) incolores les ions fer (III) Fe3+(aq) forment des ions thiocyanatofer (III) [FeSCN]2+(aq) colorés en solution aqueuse.
Données :
- Masse molaire du fer : 𝑀(Fe) = 55,8 g ⋅ mol−1
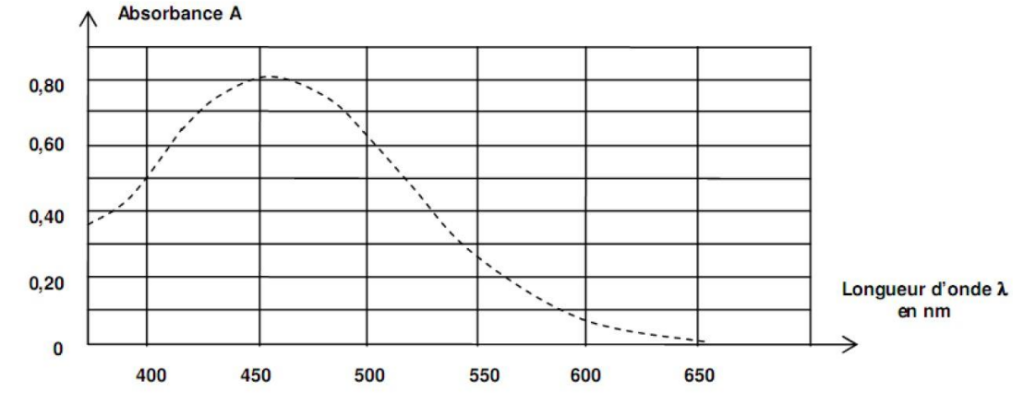
- Spectre d’absorption des ions thiocyanatofer (III) [FeSCN]2+(aq) en solution aqueuse :
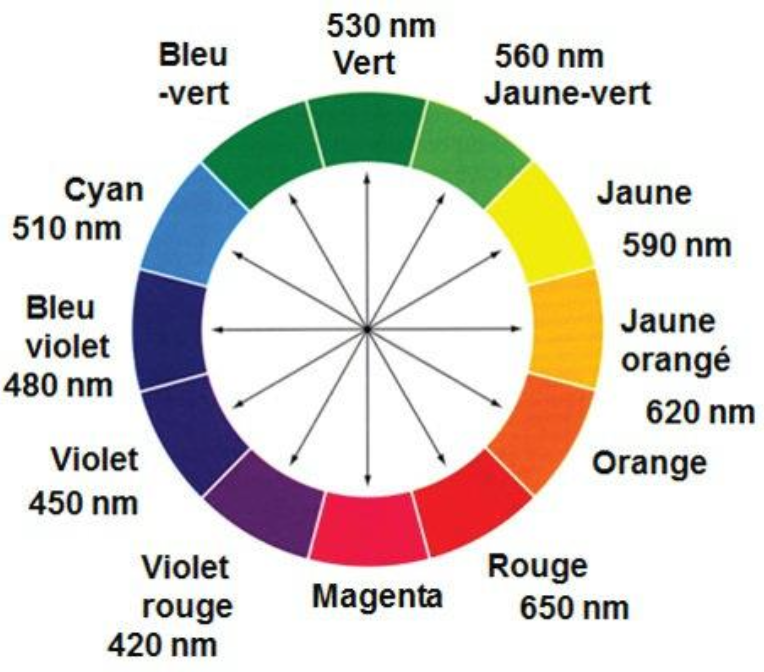
- Cercle chromatique :
- Équation de la réaction modélisant la transformation qui se produit lors du test de détection :
Fe3+(aq) + SCN−(aq) ⇄ [FeSCN]2+(aq)
- Constante d’équilibre 𝐾 associée à cette réaction à 25°C : 𝐾 = 130.
A.1. Déterminer, en justifiant, la couleur d’une solution contenant des ions thiocyanatofer (III) [FeSCN]2+(aq).
$$\lambda_{max}=460\ nm$$
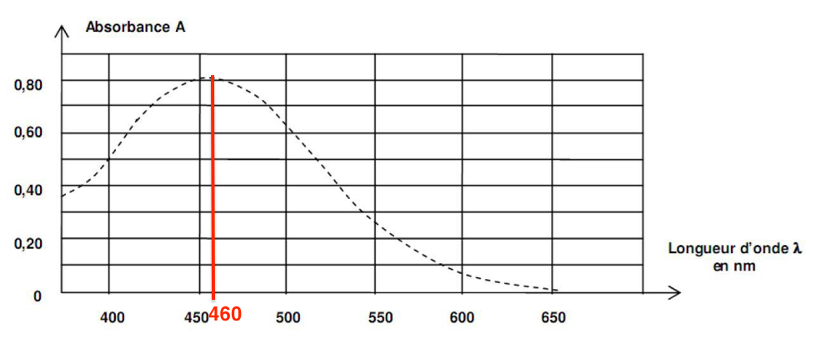
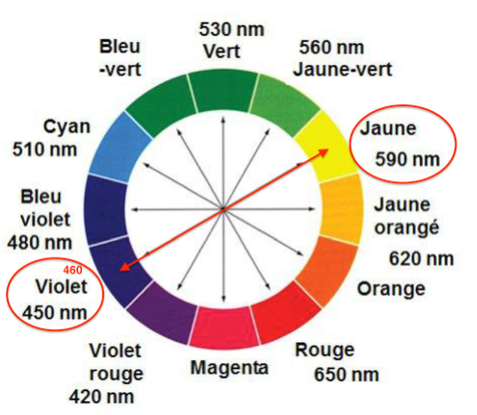
La solution contenant des ions thiocyanatofer (III) absorbe dans le violet, sa couleur est la couleur complémentaire : la solution contenant des ions thiocyanatofer (III) est jaune.
On dissout une quantité de matière 𝑛1 = 1,0 × 10−3 mol d’ions fer (III) Fe3+(aq) et une quantité de matière 𝑛2 = 5,0 × 10−4 mol d’ions thiocyanate SCN−(aq) dans un volume 𝑉 = 500,0 mL d’eau.
A.2.1. Exprimer puis calculer le quotient réactionnel initial 𝑄r,0.
$${\rm Fe}^{3+}(aq)+{\rm SCN}^-(aq)\rightarrow\left[FeSCN\right]^{2+}(aq)$$
$$Q_r=\frac{\left[\left[FeSCN\right]^{2+}\right]}{\left[{\rm Fe}^{3+}\right]\times\left[{\rm SCN}^-\right]}$$
$$Q_{r,0}=\frac{\left[\left[FeSCN\right]^{2+}\right]_0}{\left[{\rm Fe}^{3+}\right]_0\times\left[{\rm SCN}^-\right]_0}$$
Or à l’instant initial : $\left[\left[FeSCN\right]^{2+}\right]0=0\ mol.L^{-1}$
$$Q{r,0}=\frac{0}{\left[{\rm Fe}^{3+}\right]_0\times\left[{\rm SCN}^-\right]_0}$$
$$Q{r,0}=0$$
A.2.2. En déduire le sens d’évolution spontané de la transformation.
$Q_{r,0}<K$ : le sens d’évolution spontané de la transformation est le sens direct.
PARTIE B : Analyse d’un échantillon
Les eaux qui ruissellent sur les sols et s’y infiltrent dissolvent les différents ions qu’ils contiennent. Ainsi l’eau stockée dans les nappes phréatiques souterraines est caractéristique du sol traversé.
Afin d’évaluer la concentration en ions fer III contenus dans un sol, on dose par spectrophotométrie les ions thiocyanatofer (III) [FeSCN]2+(aq) contenus dans une solution aqueuse 𝑆 préparée comme suit :
- on introduit dans une fiole jaugée de 50,0 mL un volume 𝑉0 = 25,0 mL d’un échantillon d’eau prélevé d’une nappe phréatique ;
- on y ajoute 1 mL d’une solution aqueuse d’acide chlorhydrique à 5 mol ⋅ L−1, puis 1 mL d’une solution aqueuse de thiocyanate de potassium (K+(aq), SCN−(aq)) à 2 mol ⋅ L−1 ;
- on complète la fiole jusqu’au trait de jauge par de l’eau distillée.
B.1. Gamme d’étalonnage
Cinq solutions étalon de différentes concentrations 𝑐𝑓 sont préparées à partir d’une solution mère 𝑆m en ions Fe3+(aq) de concentration 𝑐m= 2,0 × 10−3 mol⋅L−1.
Chacune de ces solutions, de volume total 𝑉f = 50,0 mL, contient :
- un volume 𝑉𝑖 de la solution mère 𝑆m ;
- 1 mL d’une solution aqueuse d’acide chlorhydrique à 5 mol ⋅ L−1 ;
- 1 mL d’une solution aqueuse de thiocyanate de potassium (K+(aq), SCN−(aq)) à 2 mol ⋅ L−1 ;
- de l’eau distillée.
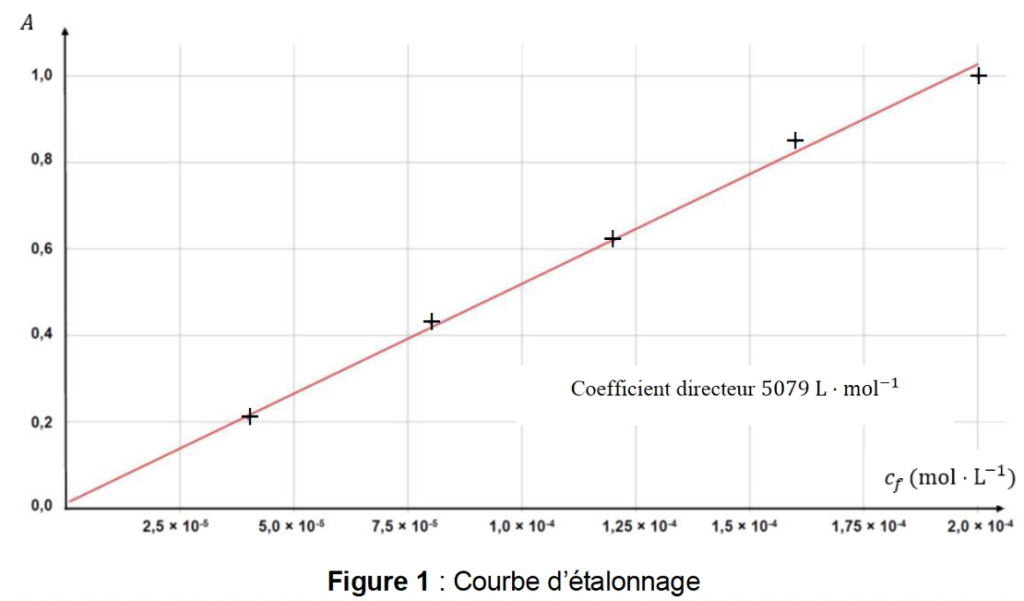
On mesure l’absorbance 𝐴 pour chacune des solutions ci-après dans le tableau et on trace la courbe d’étalonnage 𝐴 = 𝑓(𝑐𝑓) fournie sur la figure 1 page suivante.
| Solution | 1 | 2 | 3 | 4 | 5 |
| 𝑐𝑓 (mol ⋅ L−1) | 4,0 × 10−5 | 8,0 × 10−5 | 1,2 × 10−4 | 1,6 × 10−4 | 2,0 × 10−4 |
B.1.1. Préciser, en justifiant, la longueur d’onde à laquelle régler le spectrophotomètre pour réaliser les mesures d’absorbance.
Pour réaliser les mesures d’absorbance on règle le spectrophotomètre sur la longueur d’onde au maximum de l’absorbance : $\lambda_{max}=460\ nm$

B.1.2. Dresser, en justifiant, la liste du matériel nécessaire à la réalisation de la solution étalon 5 à partir de la solution mère 𝑆m.
Lors d’une dilution, la quantité de matière se conserve :
$$n_m=n_5$$
$$C_mV_m=C_5V_5$$
Avec :
- $V_m=V_i$ : un volume $V_i$ de la solution mère Sm
- $V_5=V_f$ : Chacune de ces solutions, de volume total $V_f = 50,0\ mL$, contient
$$C_mV_i=C_5V_f$$
$$V_i=\frac{C_5V_f}{C_m}$$
$$V_i=\frac{2,0\times {10}^{-4}\times 50,0\times {10}^{-3}}{2,0\times {10}^{-3}}$$
$$V_i=5,00\times {10}^{-3}\ L$$
$$V_i=5,0\ mL$$
Protocole :
- Verser la solution mère dans un bécher
- Prélever à l’aide d’une pipette jaugée Vi=5,0mL de la solution mère
- Introduire VS dans une fiole jaugée Vf=50,0mL
- Ajouter de l’eau distillée jusqu’au trait de jauge
- Homogénéiser la solution
Liste du matériel nécessaire :
- un bécher
- d’une pipette jaugée Vi=5,0mL avec une poire a pipeter
- une fiole jaugée Vf=50,0mL
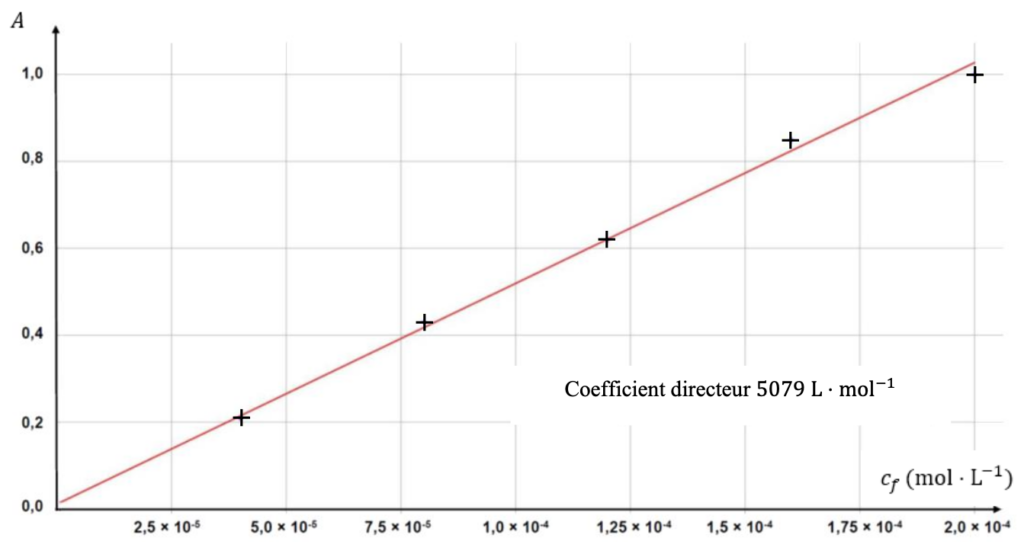
Figure 1 : Courbe d’étalonnage
B.1.3.1. Donner l’expression de la loi de Beer-Lambert en définissant chaque terme et en donnant leur unité.
Loi de Beer-Lambert :
$$A=K\times C$$
Avec
- $A$ l’absorbance sans unité
- $K$ le coefficient de proportionnalité en L.mol-1
- $C$ la concentration en mol.L-1
B.1.3.2. Indiquer si cette loi est vérifiée dans le cas étudié.
Le graphique est une droite passant par l’origine : A et C sont proportionnel ainsi A=KC . La loi de Beer Lambert est vérifiée.
B.2. Dosage de la solution 𝑺
L’absorbance de l’échantillon 𝑆 mesurée dans les mêmes conditions que pour les solutions étalons est 𝐴 = 0,70.
B.2. Déterminer la masse d’ions Fe3+(aq) contenue dans un litre d’eau de la nappe phréatique.
Dans cette question, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
$$A=K\times C$$
$$K\times C=A$$
$$C=\frac{A}{K}$$
L’absorbance de l’échantillon S mesurée dans les mêmes conditions que pour les solutions étalons est $A= 0,70$ et Figure 1 : Coefficient directeur $5079\ L\cdot mol^{-1}$.
$$C=\frac{0,70}{5079}$$
$$C=1,4\times {10}^{-4}\ mol.L^{-1}$$
Une solution aqueuse S préparée comme suit :
- on introduit dans une fiole jaugée de $50,0\ mL$ un volume $V_0 = 25,0\ mL$ d’un échantillon d’eau prélevé d’une nappe phréatique ;
L’eau prélevé d’une nappe phréatique est donc diluée 2 fois pour obtenir la solution aqueuse S.
$$C_{nape}=2C$$
$$C_{nape}=2\times 1,4\times {10}^{-4}$$
$$C_{nape}=2,8\times {10}^{-4}\ mol.L^{-1}$$
$$n_{{\rm Fe}^{3+}}=\frac{m_{{\rm Fe}^{3+}}}{M_{{\rm Fe}^{3+}}}$$
$$\frac{m_{{\rm Fe}^{3+}}}{M_{{\rm Fe}^{3+}}}=n_{{\rm Fe}^{3+}}$$
$$m_{{\rm Fe}^{3+}}=n_{{\rm Fe}^{3+}}\times M_{{\rm Fe}^{3+}}$$
Or
$$n_{{\rm Fe}^{3+}}=C_{nape}\times V$$
$$m_{{\rm Fe}^{3+}}=C_{nape}\times V\times M_{{\rm Fe}^{3+}}$$
$$m_{{\rm Fe}^{3+}}=2,8\times {10}^{-4}\times 1,0\times 55,8$$
$$m_{{\rm Fe}^{3+}}=1,6\times {10}^{-2}\ g$$
$$m_{{\rm Fe}^{3+}}=16\ mg$$
Un litre d’eau de la nappe phréatique contient une masse d’ions Fe3+(aq) de 16 mg.
