Étude d’une chaufferette

Bac Métropole Septembre 2023 Sujet 1

Exercice 2 – (4 points) –  Durée 0h42 – Calculatrice autorisée

Sujet n°23-PYCJ1ME3

Sujet et corrigé

EXERCICE 2 – ÉTUDE D’UNE CHAUFFERETTE (4 points)

Photographie d’une chaufferette commerciale

Après utilisation, on peut « régénérer » la chaufferette en la chauffant, au bain-marie par exemple, et en la laissant doucement refroidir sans perturbation pour éviter la précipitation.

Cet exercice a pour objectif de déterminer, à l’aide d’un titrage suivi par conductimétrie, le titre massique en éthanoate de sodium du contenu d’une chaufferette commerciale.

Données :

• masse molaire de l’éthanoate de sodium (Na⁺; CH₃CO₂^–) : M = 82,0 g·mol^–1 ;
• concentration maximale de l’éthanoate de sodium dans l’eau (ou solubilité) : s = 365 g·L^–1 ;
• valeurs de la conductivité molaire ionique l à 25 °C de quelques ions :

Ions	H3O+	Cℓ–	Na+	CH3CO2–
λ en mS·m2·mol–1	35,0	7,6	5,0	4,1

À partir de la solution d’éthanoate de sodium ( Na⁺; CH₃CO₂^–) présente dans la chaufferette, on prépare 50,0 mL de solution diluée 25 fois. On note S la solution obtenue.

Q1. Décrire le protocole expérimental permettant de préparer la solution S. Indiquer, en justifiant, les volumes de la verrerie utilisée.

Nous souhaitons faire une dilution de facteur 25 :
$F=\frac{V_f}{V_m}=25$
$V_f=25\times V_m$
$25\times V_m=V_f$
$V_m=\frac{V_f}{25}$
$V_m=\frac{50,0}{25}$
$V_m=2,00\ mL$

Le volume mère à prélever est de 2,00 mL.

Protocole expérimental permettant de préparer la solution S :
Prélever, à l’aide d’une pipette jaugée de 2,00 mL de la solution mère.
Introduire le prélèvement dans une fiole jaugée de 50,0 mL.
Ajouter au ¾ de l’eau distillée et homogénéiser.
Ajuster avec de l’eau distillée jusqu’au trait de jauge.
Homogénéiser.

On réalise un titrage avec suivi conductimétrique de la solution S. Pour cela un volume V_S = 10,0 mL de solution S est prélevé puis versé dans un bécher auquel sont ajoutés environ 250 mL d’eau distillée. L’ensemble est alors titré par une solution aqueuse titrante d’acide chlorhydrique de concentration C = 2,0×10–1 mol·L^–1.

La réaction support du titrage a pour équation : CH₃CO₂^–(aq) + H₃O⁺(aq) → CH₃CO₂ (aq) + H₂O(ℓ).

La conductivité σ de la solution contenue dans le bécher est mesurée après chaque ajout de solution aqueuse titrante d’acide chlorhydrique. Les résultats expérimentaux obtenus sont reproduits en figure 1 ci-dessous.

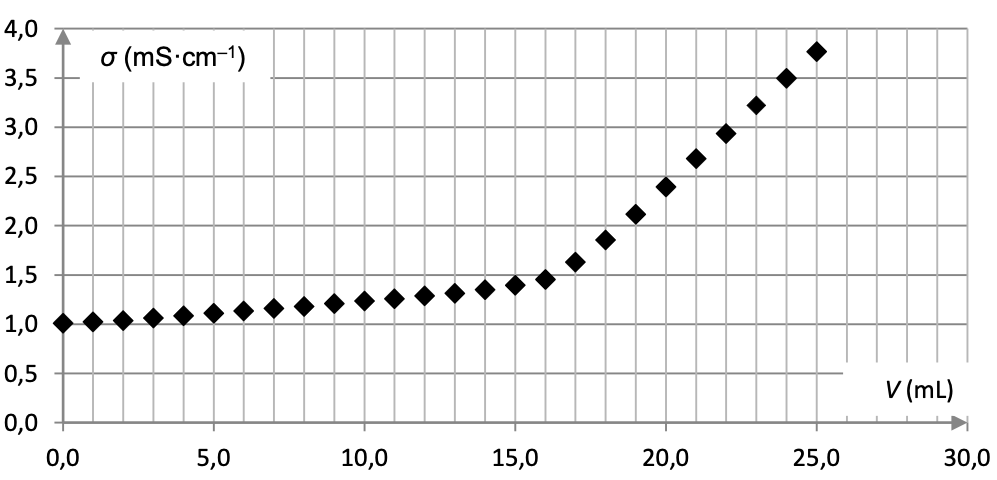
Figure 1. Représentation graphique de la conductivité σ de la solution contenue dans le bécher en fonction du volume V versé de solution aqueuse titrante d’acide chlorhydrique

Q2. Reproduire sur la copie le tableau ci-dessous. Décrire, dans chacune des cases, l’évolution des concentrations des ions dans le bécher lorsque l’on ajoute de l’acide chlorhydrique en utilisant les termes suivants :

• « reste constante » ;
• « reste négligeable » ;
• « augmente » ;
• « diminue ».

On néglige l’effet de dilution dû à l’ajout de la solution d’acide chlorhydrique dans le bécher.

Concentrations	Avant l’équivalence	Après l’équivalence
[Na+]
[CH3CO2–]
[H3O+]
[Cℓ–]

Concentrations	Avant l’équivalence	Après l’équivalence
[Na+]	reste constante	reste constante
[CH3CO2–]	diminue	reste négligeable
[H3O+]	reste négligeable	augmente
[Cℓ–]	augmente	augmente

Explication (non demandée) :
$CH_3CO_2^-(aq)+{H_3O}^+(aq)\rightarrow CH_3CO_2H(aq)+H_2O(l)$
Remarque : l’équation donnée comporte une erreur, un H (ici en rouge) à été oublié.

Avant l’équivalence :
les ions ${H_3O}^+$ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, la concentration des ions ${H_3O}^+$ est nulle (reste négligeable).
les ions ${\rm Cl}^-$ sont ajoutés, ils ne réagissent pas, la concentration des ions ${\rm Cl}^-$ augmente.
les ions $CH_3CO_2^-$ sont consommés, la concentration des ions $CH_3CO_2^-$ diminue.
Les ions ${\rm Na}^+$, présents dans la solution, ne réagissent pas : la concentration des ions ${\rm Na}^+$ ne varie pas (reste constante).

Après l’équivalence :
les ions ${H_3O}^+$ sont ajoutés et ne sont plus consommés, la concentration des ions ${H_3O}^+$ augmente.
les ions ${\rm Cl}^-$ sont ajoutés, ils ne réagissent pas, la concentration des ions ${\rm Cl}^-$ augmente.
les ions $CH_3CO_2^-$ n’existent plus, la concentration des ions $CH_3CO_2^-$ est nulle (reste négligeable).
Les ions ${\rm Na}^+$, présents dans la solution, ne réagissent pas : la concentration des ions ${\rm Na}^+$ ne varie pas (reste constante).

Q3. En utilisant les conductivités molaires ioniques des espèces présentes, justifier sans calcul l’allure de la courbe de la figure 1.

Avant l’équivalence, les ions $CH_3CO_2^-$ sont remplacés par des ions ${\rm Cl}^-$.
Or $\lambda_{{\rm Cl}^-}>\lambda_{CH_3CO_2^-}$ ainsi $\mathbf{\sigma}$ augmente légèrement avant l’équivalence.
Après l’équivalence, la concentration des ions augmente, ainsi $\mathbf{\sigma}$ augmente après l’équivalence.

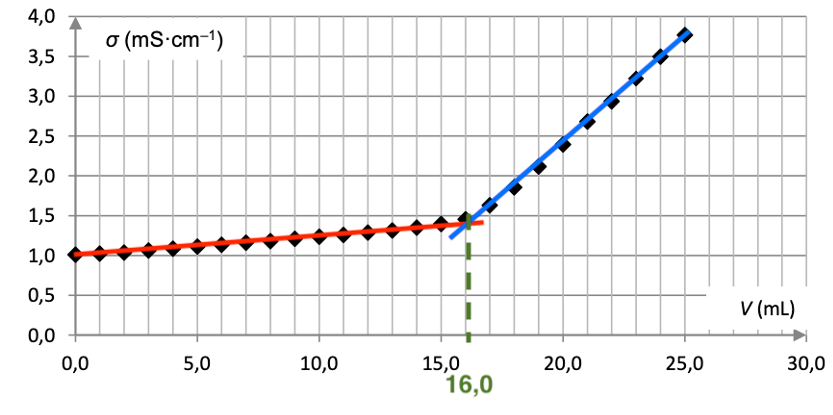
Q4. Déterminer, en justifiant à l’aide d’un schéma, la valeur du volume de solution aqueuse titrante versé à l’équivalence du titrage.

Q5. Justifier que la solution contenue dans la chaufferette est sursaturée, c’est-à-dire que sa concentration en masse de soluté est supérieure à sa solubilité s.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.

Calculons la concentration en éthanoate de sodium de la solution S.

L’équivalence est atteinte lorsque les réactifs sont introduits dans des proportions stœchiométriques.
$CH_3CO_2^-(aq)+{H_3O}^+(aq)\rightarrow CH_3CO_2H(aq)+H_2O(l)$

A l’équivalence :
$\frac{n_{CH_3CO_2^-}^i}{1}=\frac{n_{{H_3O}^+}^{eq}}{1}$
$C_S\times V_S=C\times V_{Eq}$
$C_S=\frac{C\times V_{Eq}}{V_S}$
$C_S=\frac{2,0\times{10}^{-1}\times16\times{10}^{-3}}{10,0\times{10}^{-3}}$
$C_S=0,32\ mol{.L}^{-1}$

Calculons la concentration en éthanoate de sodium de la solution chaufferette.
La solution a été diluée 25 fois :
$F=\frac{C_{chaufferette}}{C_S}=25$
$C_{chaufferette}=25\times C_S$
$C_{chaufferette}=25\times0,32$
$C_{chaufferette}=8,0\ mol{.L}^{-1}$

Calculons la concentration massique en éthanoate de sodium du contenu d’une chaufferette commerciale.
$C_m=C_{chaufferette}\times M$
$C_m=8,0\times82,0$
$C_m=656\ g{.L}^{-1}$

D’après les données, la concentration maximale de l’éthanoate de sodium dans l’eau (ou solubilité) : $s=365\ g{.L}^{-1}$.
$C_m>s$ : la solution contenue dans la chaufferette est sursaturée