Le miel et les abeilles

Bac Nouvelle Calédonie 2023 Sujet 2

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°23-PYCJ2NC1

Sujet et corrigé

EXERCICE I – LE MIEL ET LES ABEILLES (9 points)

Les abeilles sont capables de communiquer entres elles pour repérer les sources de nourriture et les sources de danger. Elles récoltent le nectar des fleurs pour le transformer en miel. Les miels vendus dans le commerce sont régulièrement analysés pour détecter d’éventuelles fraudes.

Les parties A, B et C de l’exercice sont indépendantes.

Partie A : Du nectar au miel

Les abeilles utilisent le nectar présent dans les fleurs pour fabriquer leur miel. Le nectar est aspiré par la trompe de la butineuse, puis il est emmagasiné dans son jabot où il est transformé en raison de l’absorption d’eau et de l’apport de salive riche en invertase. De retour à la ruche, la butineuse régurgite le contenu de son jabot aux ouvrières qui poursuivent la transformation dans leurs propres jabots.

Lors de cette transformation, le saccharose présent dans le nectar réagit avec l’eau pour former du glucose et du fructose qui sont les principaux constituants du miel. La molécule d’eau

« casse » la molécule de saccharose en deux. On parle d’hydrolyse du saccharose. Cette transformation chimique est une transformation totale.

L’équation de la réaction d’hydrolyse est la suivante :

C₁₂H₂₂O₁₁ + H₂O → C₆H₁₂O₆ + C₆H₁₂O₆

saccharose (S) +eau → glucose (G) +fructose (F)

La température à l’intérieur de la ruche reste égale à 35 °C.

On se propose de déterminer l’ordre de la réaction d’hydrolyse du saccharose.

À température constante, à 𝑝𝐻 = 5 constant, on mélange du saccharose avec de l’eau (sans invertase) et on suit l’évolution de la concentration du saccharose en fonction du temps. On obtient le graphique représenté sur la figure 1. [S] désigne la concentration en saccharose à l’instant 𝑡 :

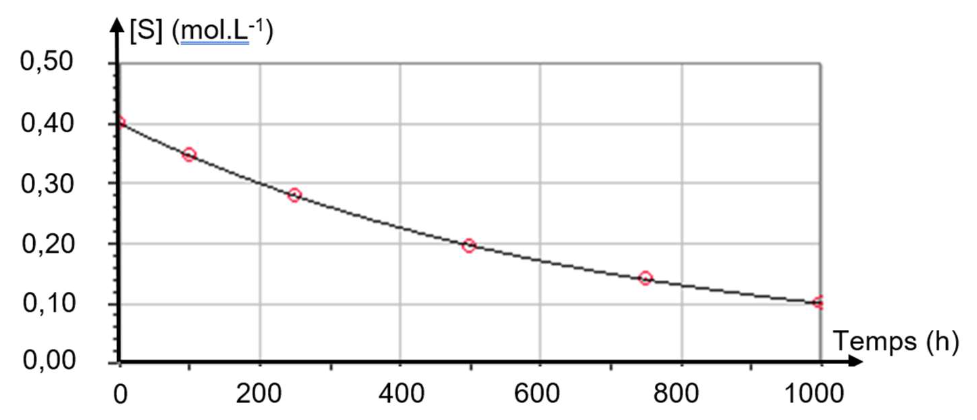
Figure 1 : Graphique représentant l’évolution de la concentration [S] en fonction du temps.

Source : dlecorgnechimie.fr

A.1. Justifier en quoi la transformation chimique peut être considérée comme lente.

L’évolution de la concentration du saccharose montre que la transformation n’est pas instantanée : la transformation chimique peut être considérée comme lente.

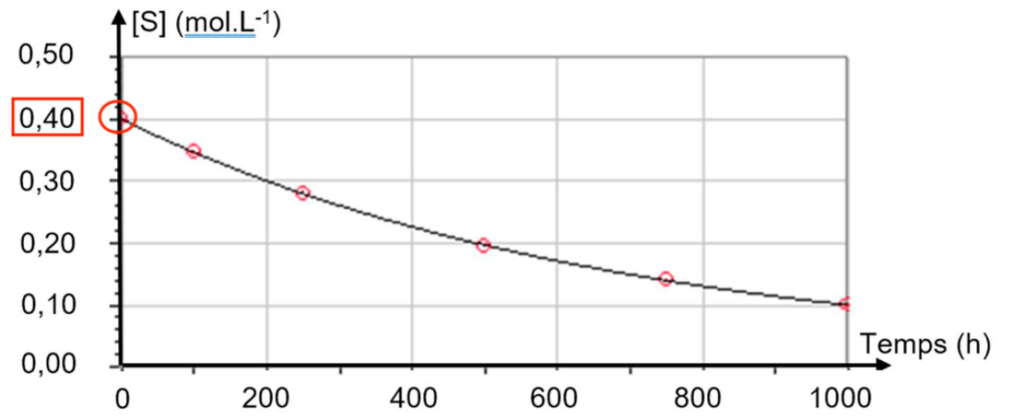
A.2. En utilisant la figure 1, déterminer la concentration initiale en saccharose [S]₀.

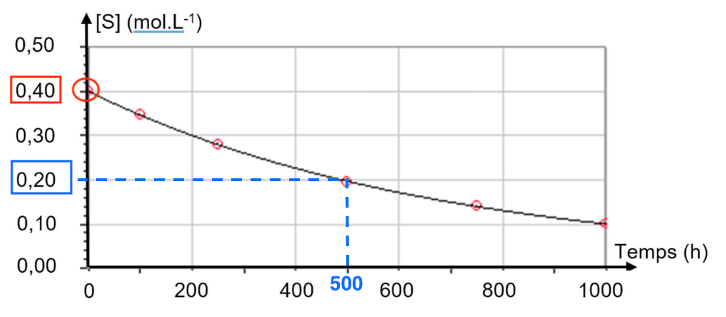
A.3. Estimer, en expliquant la démarche, la valeur du temps de demi-réaction 𝑡_1/2.

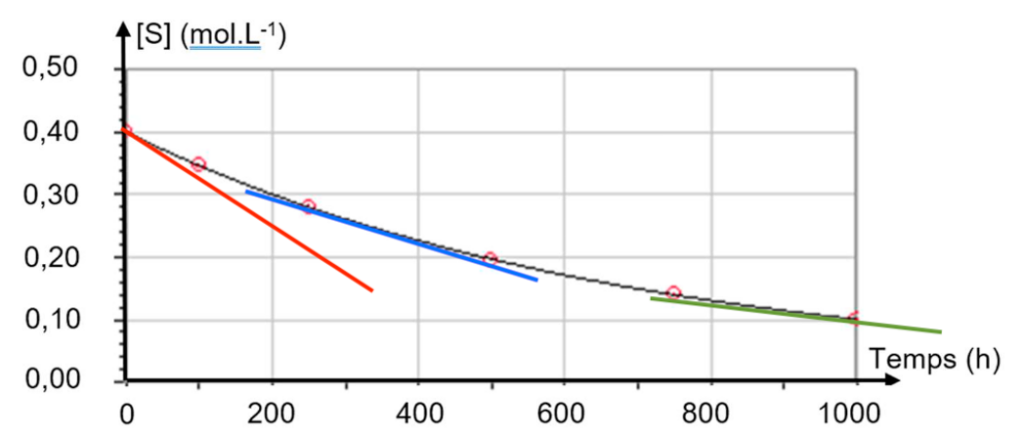
A.4. Définir la vitesse volumique de disparition 𝑣_disp du saccharose en fonction de la concentration en saccharose [S].

$v_{disp}=-\frac{d\left[S\right]_{(t)}}{dt}$

A.5. Indiquer, en justifiant qualitativement, comment varie la vitesse de disparition du saccharose au cours du temps.

On fait l’hypothèse que l’hydrolyse du saccharose suit une loi de vitesse d’ordre 1. Dans ce cas, on montre que la concentration en saccharose [S] vérifie la relation ln[S] = −𝑘 × 𝑡 + ln[S]₀ avec 𝑡 le temps (en h), 𝑘 la constante de vitesse à la température de l’expérience (en h^–1) et ln[S]₀ le logarithme népérien de la concentration initiale en saccharose (sans unité).

Les valeurs de ln[S] ont été calculées puis modélisées par la fonction ln[S] = −𝑘 × 𝑡 + ln[S]₀ à l’aide d’un programme Python. On obtient alors le graphique représenté sur la figure 2.

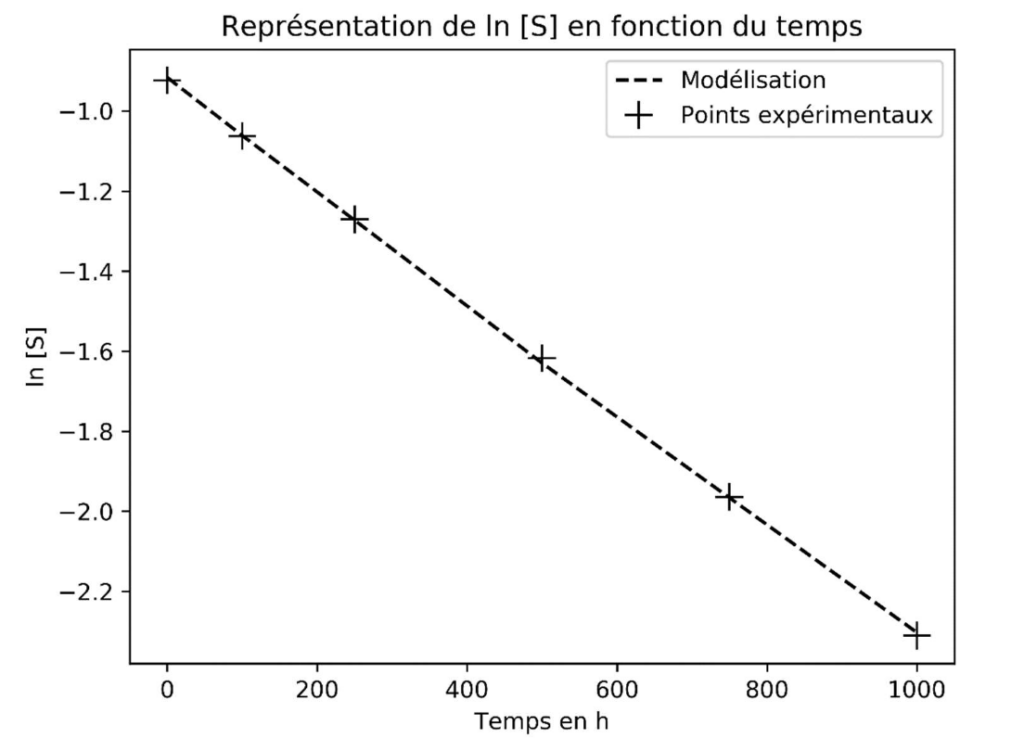
Figure 2 : Graphique représentant les données expérimentales et la modélisation.

A.6. À partir de la modélisation représentée sur la figure 2, justifier que l’hypothèse de la cinétique d’ordre 1 est validée.

Les données expérimentales correspondent à la courbe de la modélisation $\ln\left[S\right]=-k\times t+\ln\left[S\right]_0$ (figure 2).
Or lorsque la concentration en saccharose [S] vérifie la relation $\ln\left[S\right]=-k\times t+\ln\left[S\right]_0$ elle suit une loi de vitesse d’ordre 1.
Ainsi, l’hypothèse de la cinétique d’ordre 1 est validée.

Partie B : Mesure de l’acidité libre d’un miel de châtaignier

Le miel de châtaignier est majoritairement constitué de sucres (77 %) et d’eau (19 %) et son 𝑝𝐻 est égal à 4,5. Le principal acide présent dans le miel est l’acide gluconique dont la formule topologique est :

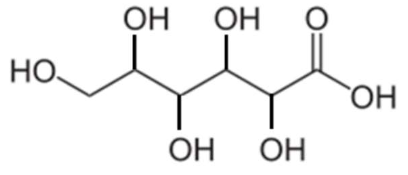
Par souci de simplification, on considèrera que l’acide gluconique est le seul acide présent dans le miel.

La teneur en acidité libre d’un miel s’exprime en milli-équivalents d’acide par kg de miel (mEq/kg). Elle correspond à la quantité de matière en mmol d’acide gluconique présent dans 1,0 kg de miel. Pour respecter la règlementation européenne, l’acidité libre d’un miel ne doit pas dépasser 50 mEq/kg.

Données :

• Couple acido-basique acide gluconique / ion gluconate : C₅H₁₁O₅COOH(aq) / C₅H₁₁O₅COO^–(aq)
• Constante d’acidité du couple acide gluconique / ion gluconate en solution aqueuse à 25 °C : 𝑝𝐾_a = 3,3.

Protocole pour mesurer l’acidité libre du miel :

• Préparer un bécher avec 50,0 mL de solution aqueuse contenant 5,00 g de miel.
• Remplir la burette graduée avec la solution titrante d’hydroxyde de sodium (Na⁺(aq) + HO^–(aq)) de concentration 𝐶_B = 1,00 × 10^–2 mol · L^–1.
• Placer la sonde 𝑝𝐻-métrique dans le bécher et mettre en marche l’agitateur magnétique.
• Tracer la courbe représentant le 𝑝𝐻 en fonction du volume de la solution titrante.

On obtient le graphique suivant :

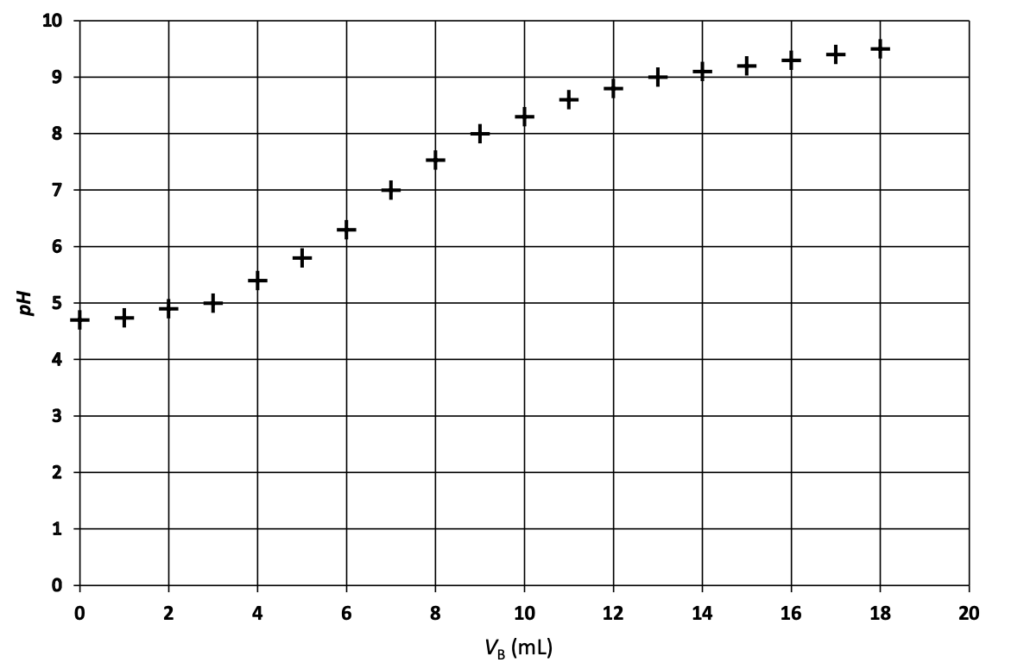
Figure 3 : Graphique représentant l’évolution du 𝑝𝐻 de la solution titrée en fonction du volume 𝑉_B de solution titrante versé.

B.1. Donner la définition d’un acide selon Brönsted.

Selon Brönsted : un acide est une espèce capable de perdre un proton $H^+$.

B.2. Si on considère que l’acide gluconique est le seul acide présent dans le miel, écrire l’équation de la réaction support du titrage.

Équation de la réaction support du titrage :
$${C_5H_{11}O_5COOH}{(aq)}+{\rm HO}{(aq)}^-\rightarrow{C_5H_{11}O_5COO}{(aq)}^-+{H_2O}{(l)}$$

B.3. Définir l’équivalence d’un titrage.

L’équivalence correspond au mélange stœchiométrique des réactifs pour la réaction mis en jeu. A l’équivalence, il y a changement du réactif limitant.

B.4. Déterminer si le miel de châtaignier respecte la règlementation européenne.

Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche, même non aboutie, sera valorisée.

A l’équivalence :
$$\frac{n_{C_5H_{11}O_5COOH}^i}{1}=\frac{n_{{\rm HO}^-}^{eq}}{1}$$
$$n_{C_5H_{11}O_5COOH}^i=C_B\times V_{eq}$$

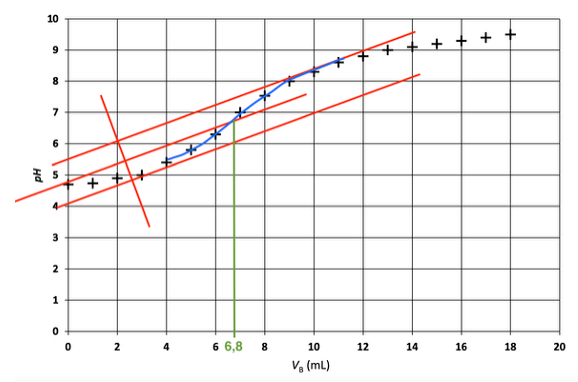
$$n_{C_5H_{11}O_5COOH}^i=1,00\times{10}^{-2}\times6,8\times{10}^{-3}$$
$$n_{C_5H_{11}O_5COOH}^i=6,8\times{10}^{-5}\ mol$$

La teneur en acidité libre d’un miel s’exprime en milli-équivalents d’acide par kg de miel (mEq/kg). Elle correspond à la quantité de matière en mmol d’acide gluconique présent dans 1,0 kg de miel.

Calculons la quantité de matière en mmol d’acide gluconique présent dans 1,0 kg de miel :

Quantité de matière	Masse de miel correspondante
$n_{C_5H_{11}O_5COOH}^i=6,8\times{10}^{-5}\ mol$	5,00 g
n	1,00 Kg

$$n=\frac{1,00\times{10}^3\times6,8\times{10}^{-5}}{5,00}$$
$$n=1,4\times{10}^{-2}\ mol$$
$$n=14\times{10}^{-3}mol$$
$$n=14\ mmol$$

La teneur en acidité libre de ce miel est 14 mEq/kg.
Pour respecter la règlementation européenne, l’acidité libre d’un miel ne doit pas dépasser 50 mEq/kg.
Ainsi, le miel de châtaignier respecte la règlementation européenne car son acidité libre est inférieure à 50 mEq/kg.

Partie C : Phéromone d’attaque de l’abeille

Pour transmettre un message chimique, les abeilles émettent des substances chimiques aux odeurs particulières, appelées phéromones. La phéromone d’attaque est l’éthanoate de 3-méthylbutyle qui est produite par des cellules bordant la poche à venin.

L’éthanoate de 3-méthylbutyle peut être synthétisé en laboratoire à partir du 3-méthylbutan-1-ol et de l’anhydride éthanoïque. La transformation chimique correspondante est modélisée par l’équation bilan ci-dessous :

C₅H₁₂O  + C₄H₆O₃ →  C₇H₁₄O₂  +  C₂H₄O₂

3-méthylbutan-1-ol +  Anhydride éthanoïque → Ethanoate de 3-méthylbutyle + acide éthanoïque

Protocole : Pour obtenir l’éthanoate de 3-méthylbutyle, on chauffe à reflux un volume 𝑉₁ = 9,9 mL de 3-méthylbutan-1-ol avec un volume 𝑉₂ = 8,6 mL d’anhydride éthanoïque, en présence d’acide sulfurique. Après séparation et rinçage, on obtient une quantité de matière finale d’éthanoate de 3-méthylbutyle 𝑛_ƒ = 7,4 × 10^–2 mol.

Données :

Espèces chimiques	Masse molaire (g · mol–1)	Masse volumique p (g · mL–1)	Température d’ébullition (°C)	Solubilité dans l’eau
3-méthylbutan-1-ol	88,1	0,81	128	Très peu soluble
Anhydride éthanoïque	102,1	1,08	139	Très soluble
Éthanoate de 3-méthylbutyle	130,2	0,87	142	Très peu soluble

C.1. Justifier le double intérêt du chauffage à reflux.

Un chauffage à reflux permet d’accélérer la réaction sans perte de matière.

C.2. À l’aide du protocole et des données, vérifier que la quantité de matière initiale du 3-méthylbutan-1-ol est 𝑛₁ = 9,1 × 10^–2 mol et que la quantité de matière initiale d’anhydride éthanoïque est 𝑛₂ = 9,1 × 10^–2 mol.

$$n=\frac{m}{M}$$

Or
$$\rho=\frac{m}{V}$$
$$\frac{m}{V}=\rho$$
$$m=\rho\times V$$

$$n=\frac{\rho\times V}{M}$$

Ainsi :
$$n_1=\rho_{3\text{-méthylbutan-1-ol}\times}V_{3\text{-méthylbutan-1-ol}}/M_{3\text{-méthylbutan-1-ol}}$$
$$n_1=\frac{0,81\times9,9}{88,1}$$
$$n_1=9,1\times{10}^{-2}\ mol$$

$$n_2=\rho_{anhydride\ éthanoïque}\times V_{anhydride\ éthanoïque}/M_{anhydride\ éthanoïque}$$
$$n_2=\frac{1,08\times8,6}{102,1}$$
$$n_2=9,1\times{10}^{-2}\ mol$$

C.3. Montrer que le rendement de la synthèse est d’environ 81 %.

Équation		C5H12O  +   C4H6O3   →  C7H14O2    +     C2H4O2
État initial	x=0mol	$9,1\times{10}^{-2}-x$	$9,1\times{10}^{-2}-x$	0	0
État intermédiaire	x	$9,1\times{10}^{-2}-x$	$9,1\times{10}^{-2}-x$	x	x
État final	x=xf	$9,1\times{10}^{-2}-x_f$	$9,1\times{10}^{-2}-x_f$	xf	xf

Équation C5H12O + C4H6O3 → C7H14O2 + C2H4O2
État initial $x=0mol$ $9,1\times{10}^{-2}$ $9,1\times{10}^{-2}$ 0 0
État intermédiaire $x$ $9,1\times{10}^{-2}-x$ $9,1\times{10}^{-2}-x$ $x$ $x$
État final $x=x_f$ $9,1\times{10}^{-2}-x_f$ $x_f$ $x_f$

Calculons $x_{max}$ :
$$9,1\times{10}^{-2}-x_{max}=0$$
$$x_{max}=9,1\times{10}^{-2}\ mol$$

D’après le texte : n obtient une quantité de matière finale d’éthanoate de 3-méthylbutyle (C7H14O2)
$$n_f=7,4\times{10}^{-2}\ mol.$$

Calculons $x_f$ :
$$x_f=7,4\times{10}^{-2}\ mol$$

Calculons le rendement :
$$\eta=\frac{n_{exp}}{n_{Th}}$$
$$\eta=\frac{x_f}{x_{max}}$$

$$\eta=\frac{7,4\times{10}^{-2}}{9,1\times{10}^{-2}}=0,81=81%$$

C.4. Proposer une méthode permettant d’améliorer ce rendement.

Pour augmenter le rendement, on peut déplacer l’équilibre en :

• Mettant un réactif en excès
• En séparant les produits au fur et à mesure de leur formation.