E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02711, n°G1SPHCH02735 et n°G1SPHCH02780
Télécharger l’exercice en PDF :

La bouillie bordelaise peut être utilisée par les jardiniers pour traiter le potager ou les arbres fruitiers contre certaines maladies. Dans le commerce, elle est vendue sous la forme d’une poudre à dissoudre dans de l’eau.
Cette poudre est constituée de sulfate de cuivre hydraté CuSO4,5H2O(s) et d’hydroxyde de calcium Ca(OH)2(s).
On obtient, par dissolution de cette poudre dans l’eau, une solution contenant des ions cuivre Cu2+ à pulvériser sur les végétaux.
Comme tout produit de traitement, cette solution doit être utilisée en respectant des concentrations précises. En effet au-delà d’un certain seuil, le cuivre est toxique pour l’Homme et l’environnement.
Le but de l’exercice est de déterminer si la solution de bouillie bordelaise notée S, fabriquée en trop grande quantité par un jardinier amateur, peut être jetée à l’évier ou doit être traitée ou recyclée
Données :
- Concentration en masse limite d’ions Cu2+ pour les rejets dans les eaux usées : Cm = 0,5 mg par litre d’eau déversée
- Masse molaire atomique du cuivre : M(Cu) = 63,5 g·mol−1
- Masse molaire de l’hydroxyde de sodium : M(NaOH) = 40,0 g·mol−1
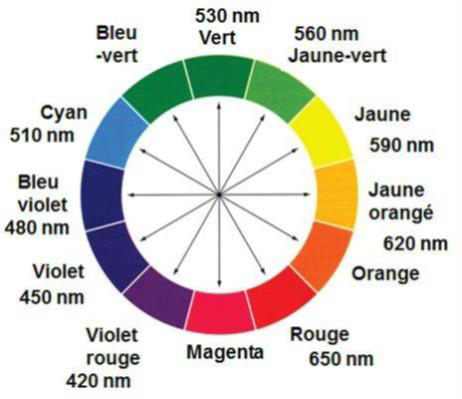
- Cercle chromatique :
- Spectre d’absorbance d’une solution aqueuse de sulfate de cuivre
(Cu2+ (aq) + SO42-(aq)) :
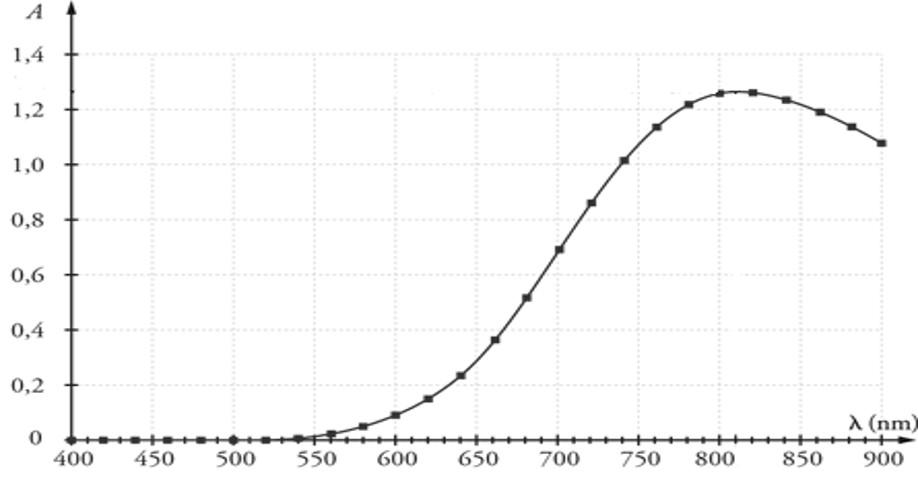
- L’espèce ionique Cu2+ (aq) est responsable de la couleur de la solution aqueuse.
1. Déterminer la couleur de l’espèce ionique Cu2+(aq) en solution aqueuse. Justifier.
« L’espèce ionique Cu2+(aq) est responsable de la couleur de la solution aqueuse. »
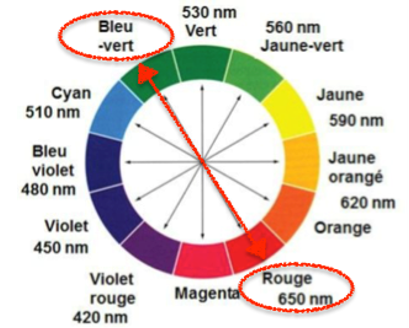
Le pic d’absorption se situe pour λ = 810 nm. Or à 810 nm nous ne sommes pas dans le visible. Nous allons regarder la partie visible qui est absorbée.
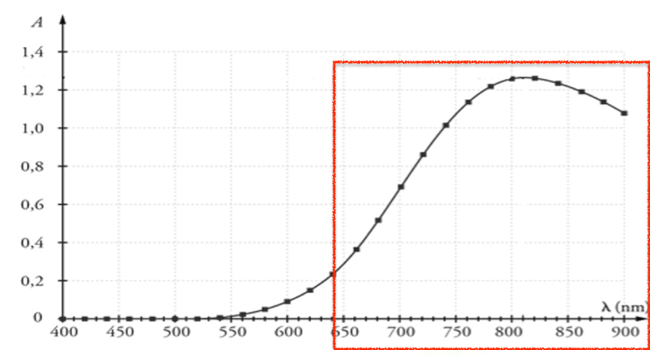
L’absorbance d’une solution est proportionnelle à la concentration (loi de Beer Lambert).
En mesurant l’absorbance de différentes solutions de concentrations connues, on trace une droite d’étalonnage. Connaissant l’absorbance d’une solution inconnue, on détermine par lecture graphique sa concentration.
On souhaite déterminer la concentration en quantité de matière d’ions cuivre Cu2+(aq) de la solution de bouillie bordelaise S, par un dosage spectrophotométrique. On réalise pour cela une gamme étalon et des mesures d’absorbance à la longueur d’onde 810 nm.
2. Expliquer en quelques lignes le principe de cette méthode de dosage.
L’absorbance d’une solution est proportionnelle à la concentration (loi de Beer Lambert).
En mesurant l’absorbance de différentes solutions de concentrations connues, on trace une droite d’étalonnage. Connaissant l’absorbance d’une solution inconnue, on détermine par lecture graphique sa concentration.
On dispose d’une solution mère de sulfate de cuivre S0 de concentration en quantité de matière d’ions cuivre Cu 2+(aq) égale à C0= 0,040 mol·L-1. À partir de cette solution S0 on prépare différentes solutions Si. Le volume de chaque solution fille obtenue est égal à VF= 10,0 mL.
3. Recopier et compléter le tableau ci-dessous en explicitant le calcul pour la solution S2.
| Solution fille Si | S1 | S2 | S3 | S4 | S5 |
| Concentration en quantité de matière Ci (mol.L-1) | 0,020 | 0,016 | 0,012 | 0,008 | 0,004 |
| Volume V0 de solution S0 à prélever (mL) |
Calcul pour la solution S2 :
Lors d’une dilution la quantité de matière se conserve :
$n_0=n_2$
Or
$n=C\times V$
Donc
$C_0 V_0=C_2 V_2$
$V_0=\frac{C_2 V_2}{C_0}$
$V_0=\frac{0,016\times10,0.10^{-3}}{0,040}$
$V_0=4,0.10^{-3}\ L=4,0\ mL$
| Solution fille Si | S1 | S2 | S3 | S4 | S5 |
| Concentration en quantité de matière Ci (mol.L-1) | 0,020 | 0,016 | 0,012 | 0,008 | 0,004 |
| Volume V0 de solution S0 à prélever (mL) | 5,0 | 4,0 | 3,0 | 2,0 | 1,0 |
On mesure l’absorbance A des différentes solutions préparées et on trace le graphique suivant :
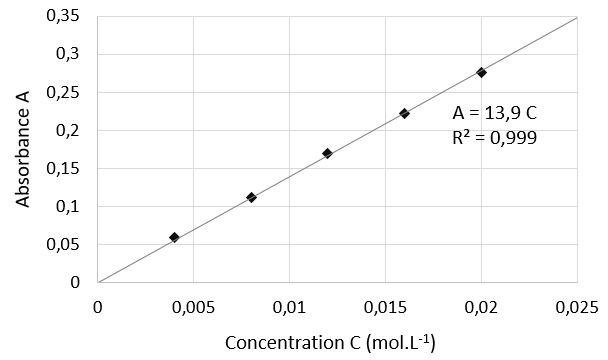
4. Après avoir rappelé l’expression de la loi de Beer-Lambert en indiquant le nom des grandeurs et les unités associées, déterminer si les résultats expérimentaux obtenus sont en accord avec cette loi.
Loi de Beer Lambert : A=K.c
Avec :
- A l’absorbance sans unité
- C la concentration en mol.L-1
- K en L.mol-1
La courbe obtenue est une droite passant par l’origine : A et C sont proportionnelles. Les résultats expérimentaux obtenus sont en accord avec la loi de Beer Lambert
Afin de déterminer la concentration de la bouillie bordelaise préparée par le jardinier, on dilue 20 fois la solution S avant de l’analyser avec le spectrophotomètre. On mesure une absorbance A’ = 0,120 pour la solution diluée S’.
5. Détailler le protocole expérimental de préparation des 100 mL de la solution S’. La verrerie mise à disposition est :
| fiole jaugée : 100 mL et 200 mL pipettes jaugées : 5 mL, 10 mL, 50 mL et 100 mL béchers : 50 mL et 100 mL | éprouvettes graduées : 10 mL, 50 mL et 100 mL pissette d’eau distillée pipette en plastique souple |
Lors d’une dilution la quantité de matière se conserve :
$n’=n$
Or
$n=C\times V$
Donc
$C’ V’=CV$
$V’=\frac{CV}{C’}$
Or on dilue 20 fois la solution S : $C=20\times C’$
$V’=\frac{20\times C’\times V}{C’}$
$V’=20V$
Remarque : on peut utiliser le facteur de dilution pour arriver au même résultat
$F=\frac{C_{mere}}{C_{fille}}=\frac{V_{fille}}{V_{mere}}$
$\frac{V_{fille}}{V_{mere}}=F$
$V_{fille}=F\times V_{mere}$
$V’=20V$
$V’$ le volume fille est celui d’une fiole jaugée et $V$ le volume de la solution mère est prélevé avec une pipette jaugée.
Ainsi nous utiliserons une fiole jaugée dont le volume est 20 fois plus grand que la pipette jaugée.
Prenons une pipette jaugée de 5,0 mL et une fiole jaugée de 100 mL.
Protocole :
Verser la solution mère dans un bécher
Prélever à l’aide d’une pipette jaugée V=5,0 mL de la solution mère
Introduire V dans une fiole jaugée 100 mL
Ajouter de l’eau distillée jusqu’au trait de jauge
Homogénéiser la solution
6. Déterminer si le jardinier peut rejeter son excédent de solution S à l’évier ou s’il doit le faire recycler.
Il faut déterminer si le jardinier peut rejeter son excédent de solution S à l’évier ou s’il doit le faire recycler.
D’après les données : « Concentration en masse limite d’ions $Cu^{2+}$ pour les rejets dans les eaux usées : $C_m = 0,5\ mg$ par litre d’eau déversée »
Il faut donc trouver sa concentration.
Non demandé mais à savoir faire : La lecture graphique n’étant pas assez précise sur ce graphique, nous allons déterminer son équation.
$k=\frac{A_B-A_A}{C_B-C_B}$
$k=\frac{0,35-0}{0,025-0}=14\ L.mol^{-1}$
Remarque : l’équation est affichée sur le graphique $A=13,9\times C$
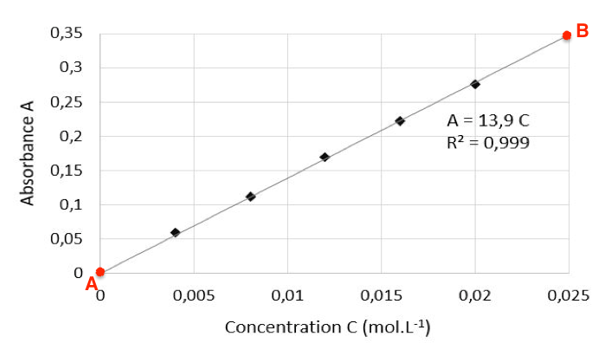
Calculons $C’$ :
$A=13,9\times C’$
$C’=\frac{A}{13,9}$
$C’=\frac{0,120}{13,9}=8,63.10^{-3}\ mol.L^{-1}$
Calculons $C$ :
$C=20\times C’$
$C=20\times8,57.10^{-3}$
$C=0,173\ mol.L^{-1}$
Calculons la concentration massique $C_m$ :
$C_m=C\times M$
$C_m=0,173\times63,5$
$C_m=11,0\ g.L^{-1}$
Cette valeur est supérieure à la concentration limite. Il ne peut pas rejeter son excédent de solution S à l’évier, il doit le faire recycler.
La toxicité de la bouillie bordelaise est liée à la présence des ions cuivre Cu2+. Un traitement pour éliminer ces ions consiste à ajouter des pastilles d’hydroxyde de sodium NaOH(s). La transformation est modélisée par la réaction des ions cuivre Cu2+ présents dans la bouillie bordelaise et des ions hydroxyde OH– apportés par les pastilles d’hydroxyde de sodium) pour former un précipité d’hydroxyde de cuivre Cu(OH)2(s) qui est récupéré par filtration puis traité.
L’équation de la réaction chimique est la suivante :
Cu2+(aq) + 2 OH – (aq) → Cu(OH)2(s)
On souhaite traiter 500 mL d’une solution dont la concentration en quantité de matière d’ions Cu2+ est égale à CT = 0,22 mol.L-1.
7. Déterminer la masse m d’hydroxyde de sodium NaOH(s) à ajouter à cette solution pour éliminer totalement les ions cuivre sans pour autant que les ions hydroxyde ne soient en excès.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti.
L’équation de la réaction chimique est la suivante :
$Cu^{2+}(aq)+2OH^-(aq)\rightarrow Cu(OH)_2(s)$
Pour éliminer totalement les ions cuivre sans pour autant que les ions hydroxyde ne soient en excès, les réactifs doivent être dans les proportions stœchiométriques :
Méthode 1 :
$\frac{n_{OH^-}}{2}=n_{Cu^{2+}}$
Méthode 2 : utilisation d’un tableau d’avancement
| Équation | Cu2+(aq) | + 2 OH – (aq) | → Cu(OH)2(s) | |
| État initial | x=0mol | $n_{Cu^{2+}}$ | $n_{OH^-}$ | 0 |
| État intermédiaire | x | $n_{Cu^{2+}}-x$ | $n_{OH^-}-2x$ | x |
| État final | x=xf | $n_{Cu^{2+}}-x_f$ | $n_{OH^-}-2x_f$ | xf |
Pour éliminer totalement les ions cuivre :
$n_{Cu^{2+}}-x_f=0$
$-x_f=-n_{Cu^{2+}}$
$x_f=n_{Cu^{2+}}$
Sans pour autant que les ions hydroxyde ne soient en excès :
$n_{OH^-}-2x_f=0$
$-2x_f=-n_{OH^-}$
$2x_f=n_{OH^-}$
$x_f=\frac{n_{OH^-}}{2}$
Ainsi :
$\frac{n_{OH^-}}{2}=n_{Cu^{2+}}$
Or $n_{OH^-}=n_{NaOH}=\frac{m_{NaOH}}{M_{NaOH}}$
et $n_{Cu^{2+}}=C_T V$
D’où
$\frac{m_{NaOH}}{2M_{NaOH}}=C_T V$
$m_{NaOH}=2\times C_T\times V\times M_{NaOH}$
$m_{NaOH}=2\times0,22\times500.10^{-3}\times40,0$
$m_{NaOH}=8,8\ g$
Il doit ajouter $8,8g$ d’hydroxyde de sodium à cette solution pour éliminer totalement les ions cuivre sans pour autant que les ions hydroxyde ne soient en excès.
