Synthèse du polycarbonate de bisphénol

Nouvelle Calédonie 2022 Sujet 2

Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 22-PYCJ2NC1

[latexpage]

Le principal polycarbonate commercial est le polycarbonate de bisphénol A. Il s’agit d’un polymère de formule indiquée ci-après :

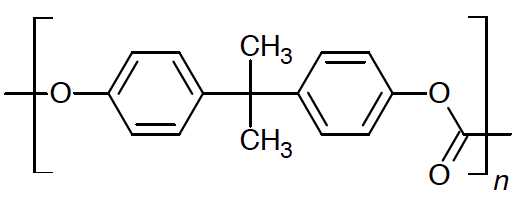
Cette matière est transparente, résistante aux chocs et utilisable dans une large gamme de températures, ce qui en fait un matériau de choix dans la fabrication de nombreux objets : verres de vue, fenêtres, CD et DVD, vitres de phares automobiles, etc.

La méthode la plus utilisée pour la fabrication de ce polycarbonate est une réaction de polymérisation du bisphénol A avec du phosgène COCl₂ en présence de soude dans un solvant organique chloré comme le dichlorométhane CH₂Cl₂.

L’équation de la réaction modélisant la polymérisation est la suivante :

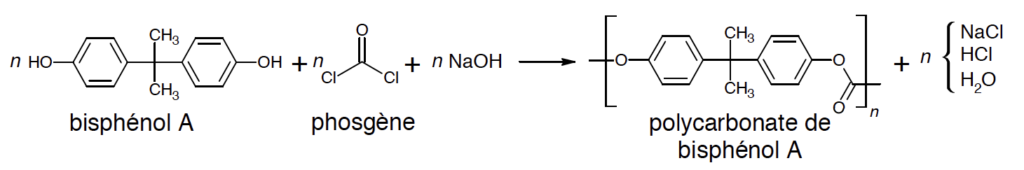
Cet exercice comporte deux parties, qui peuvent être traitées indépendamment l’une de l’autre.

Données :

Le phosgène COCl₂ est un composé ininflammable et inexplosible mais dangereux. Il a été utilisé comme gaz de combat lors de la première guerre mondiale.

Source : INRS, institut national de recherche et de sécurité.

Masses molaires atomiques :
- M_H = 1,0 g·mol ^-1
- M_C = 12,0 g·mol ^-1
- M_O = 16,0 g·mol ^-1
- M_N = 14,0 g·mol ^-1
- M_Na = 23,0 g·mol ^-1
- M_Cl = 35,5 g·mol ^-1
Masse molaire du bisphénol A : 223 g·mol^-1
Masse molaire du phosgène : 99,0 g·mol^-1
Masse molaire du motif du polycarbonate de bisphénol A : 254 g.mol^-1

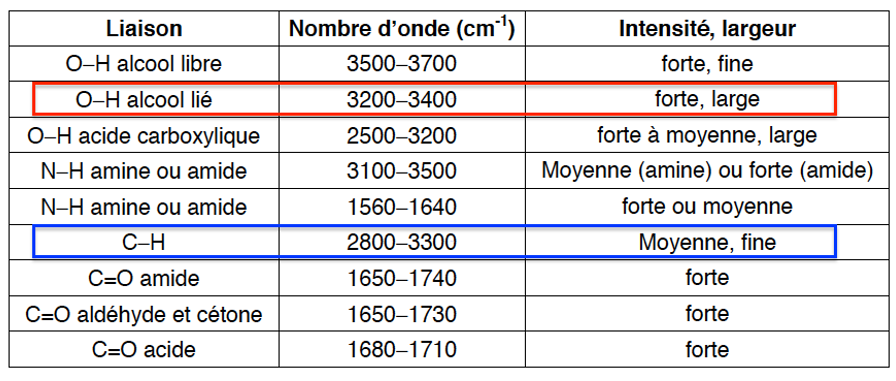
Table de données de spectroscopie infrarouge :

Liaison	Nombre d’onde (cm^-1)	Intensité, largeur
O-H alcool libre	3500-3700	forte, fine
O-H alcool lié	3200-3400	forte, large
O-H acide carboxylique	2500-3200	forte à moyenne, large
N-H amine ou amide	3100-3500	Moyenne (amine) ou forte (amide)
N-H amine ou amide	1560-1640	forte ou moyenne
C-H	2800-3300	Moyenne, fine
C=O amide	1650-1740	forte
C=O aldéhyde et cétone	1650-1730	forte
C=O acide	1680-1710	forte

Partie A : Étude des réactifs

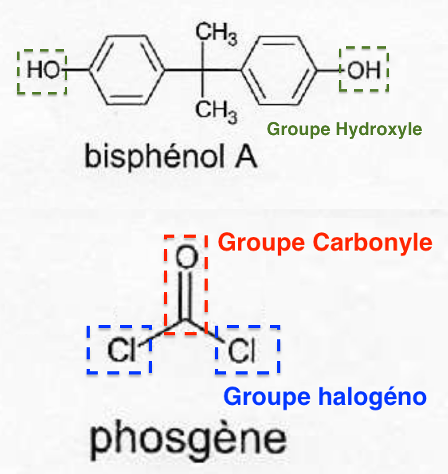
A.1. Identifier les groupes caractéristiques présents dans le bisphénol A et le phosgène.

A.2. Le phosgène est produit industriellement par introduction de dichlore Cl₂ et de monoxyde de carbone CO gazeux dans un réacteur à 250 °C. La transformation se produisant dans le réacteur est modélisée par la réaction d’équation suivante :

CO (g) + Cl₂ (g) → COCl₂ (g)

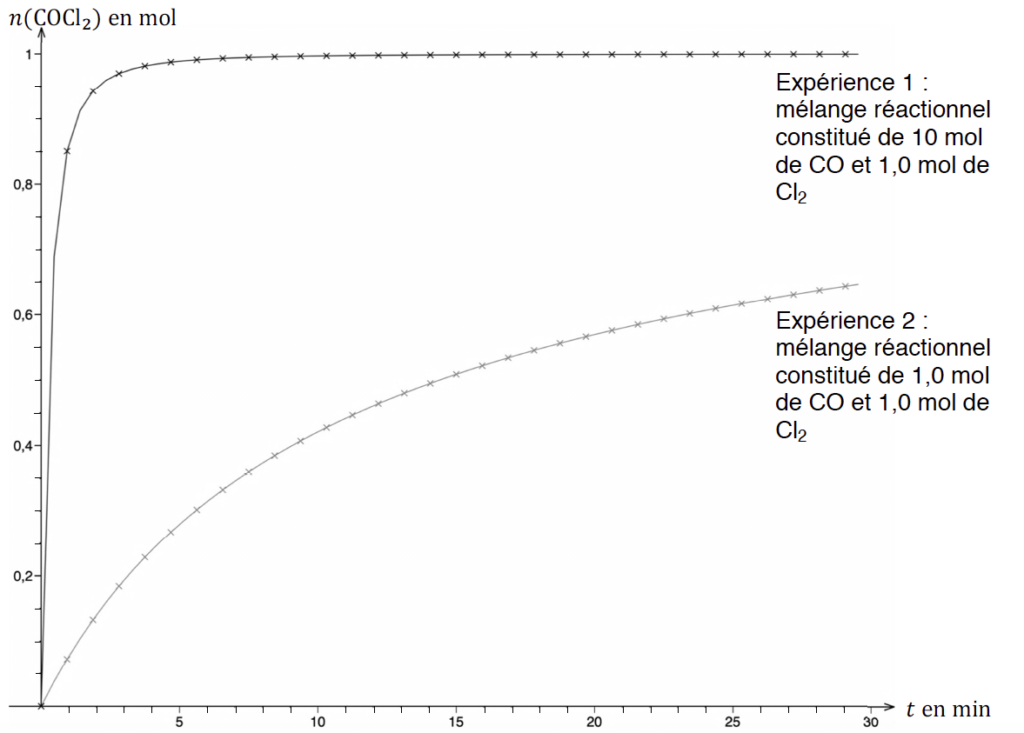
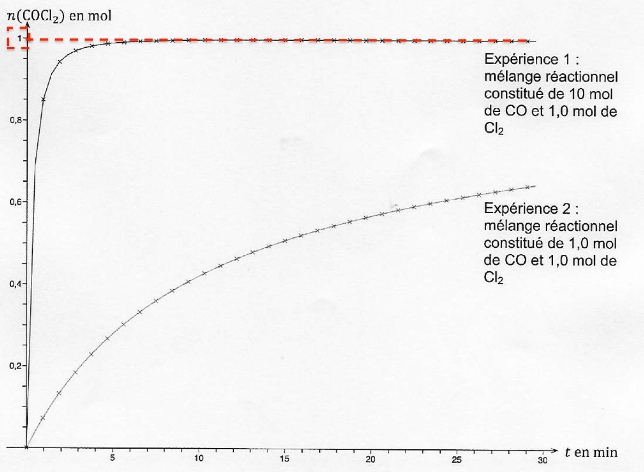
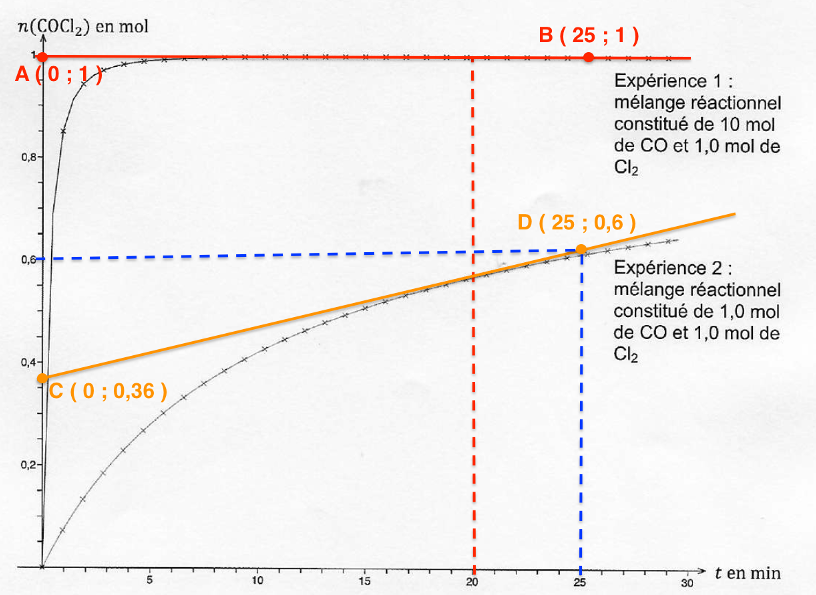
On réalise deux expériences au cours desquelles on mesure la quantité de matière de phosgène formé au cours du temps dans une enceinte de volume constant V = 30 L, à température constante T de 250 °C. Les graphiques correspondants sont donnés sur l’ANNEXE 1 À RENDRE AVEC LA COPIE (p14/15).

A.2.1. Déterminer la valeur de l’avancement final dans l’expérience 1.

Equation de la réaction		${\rm CO}{(g)}$	$+{\rm Cl}_{2(g)}$	$\rightarrow{\rm COCl}_{2(g)}$
Etat du système	Avancement (mol)	Quantités de matière (mol)
Etat initial	0	10	1,0	0
Etat intermédiaire	x	10−x	1,0−x	x
Etat final (à l’équilibre)	x_f	10−x_f	1,0−x_f	1−x_f

$$x_f=n_{{\rm COCl}_2}^f=1,0\ mol$$

A.2.2. Justifier que la synthèse du phosgène est une transformation totale, puis en déduire l’avancement final de la réaction lors de l’expérience 2.

$$10-x_{max1}=0$$
$$x_{max1}=10\ mol$$

$$1,0-x_{max2}=0$$
$$x_{max2}=1,0\ mol$$

$x_{max2}<x_{max1}$ :
$$x_{max}=1,0\ mol$$

$$\tau=\frac{x_f}{x_{max}}$$
$$\tau=\frac{1,0}{1,0}$$
$$\tau=1$$

: la réaction est totale.

L’expérience 2 donne une courbe croissante pour laquelle $x$ n’atteint pas une asymptote.

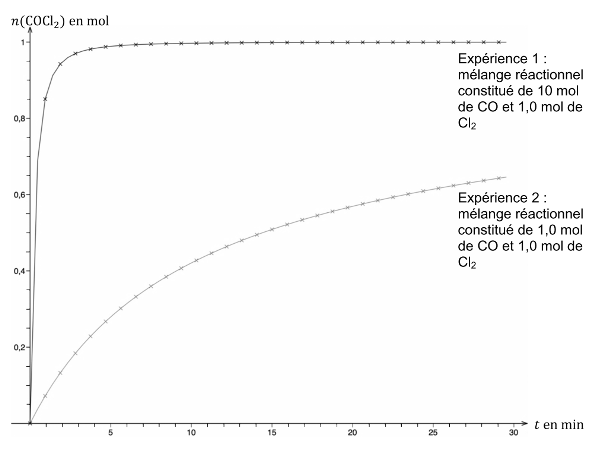
Calculons $x_{max}$ pour l’expérience 2 :
$$1,0-x_{max1}=0$$
$$x_{max1}=1,0\ mol$$

$$1,0-x_{max2}=0$$
$$x_{max2}=1,0\ mol$$

$x_{max2}=x_{max1}$ :
$$x_{max}=1,0\ mol$$

Comme la réaction est totale, $x_f=x_{max}=1,0\ mol$ pour l’expérience 2.

A.2.3. Donner la définition du temps de demi-réaction d’une transformation chimique.

t_1/2 est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : x(t_1/2) = x_f/2.

A.2.4. Déterminer graphiquement sur le document de l’ANNEXE 1 À RENDRE AVEC LA COPIE (p14/15) la valeur du temps de demi-réaction pour l’expérience 2.

Pour l’expérience 2 : t_1/2 =15 min

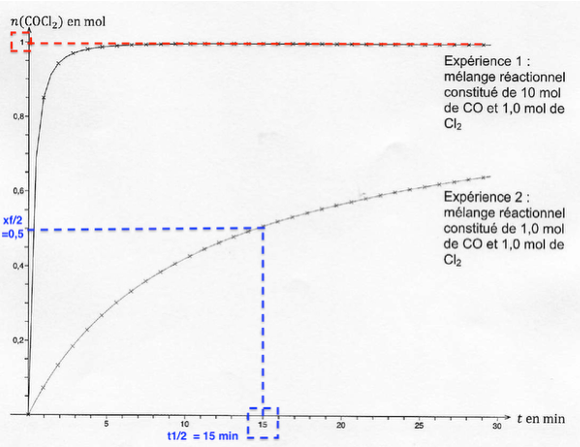
A.2.5. Comparer qualitativement le temps de demi-réaction de l’expérience 1 à celui de l’expérience 2 et justifier leur écart.

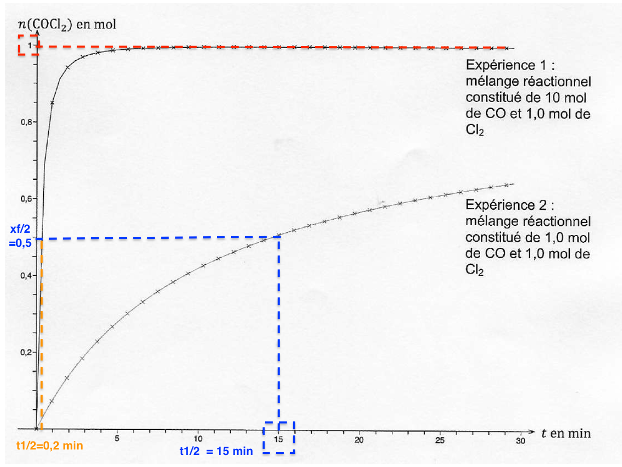
Pour l’expérience 1 : t_1/2 =0,2 min

Le temps de demi réaction de l’expérience 1 est très inferieur à celui de l’expérience 2.

Cet écart est dû au fait que dans l’expérience 1 un des réactifs est introduit en très large excès.

La définition de la concentration en quantité de matière dans un mélange de gaz est la même que dans une solution aqueuse : $C(COCl_2)=\frac{n(COCl_2)}{V_{mélange}} $

A.2.6. Calculer les vitesses volumiques de formation du phosgène à la date t = 20 minutes dans chaque expérience. Commenter ces valeurs.

$$v=\frac{1}{V}\frac{dx_{(t)}}{dt}$$

Or d’après le tableau d’avancement $x=n_{{\rm COCl}_2}$

$$v=\frac{1}{V}\frac{d{n_{{\rm COCl}2}}{(t)}}{dt}$$

La dérivée se calcule en trouvant le coefficient directeur de la tangente en un point de la courbe.

Pour l’expérience 1 à $t=20\ min$ :
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{1,0-1,0}{25-0}=0\ mol.\min^{-1}$$
$$v_{t=20\min}^1=\frac{1}{V}\frac{d{n_{{\rm COCl}2}}{(t)}}{dt}$$
$$v_{t=20\min}^1=\frac{1}{V}\times k$$
$$v_{t=20\min}^1=\frac{1}{30}\times 0$$
$$v_{t=20\min}^1=0\ mol.L^{-1}.\min^{-1}$$

Pour l’expérience 2 à $t=20\ min$ :
$$k’=\frac{y_D-y_C}{x_D-x_C}$$
$$k’=\frac{0,60-0,36}{25-0}=9,6{.10}^{-3}\ mol.\min^{-1}$$
$$v_{t=20\min}^2=\frac{1}{V}\frac{d{n_{{\rm COCl}2}}{(t)}}{dt}$$
$$v_{t=20\min}^2=\frac{1}{V}\times k’$$
$$v_{t=20\min}^2=\frac{1}{30}\times 9,6{.10}^{-3}$$
$$v_{t=20\min}^2=3,2{.10}^{-4}\ mol.L^{-1}.\min^{-1}$$

La réaction de l’expérience 1 est terminée et la réaction de l’expérience 2 n’est pas terminée.

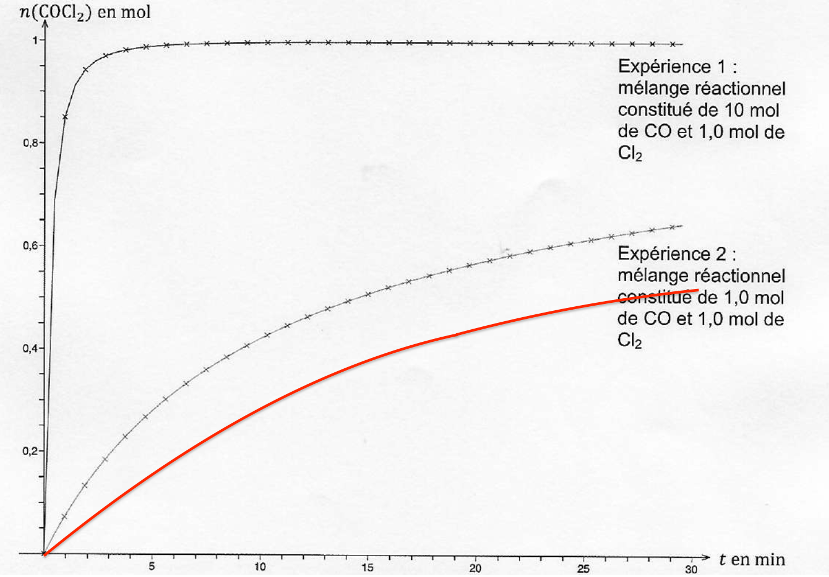
A.2.7. Un mélange réactionnel de 1,0 mol de CO et 1,0 mol de Cl₂ est introduit dans un réacteur à une température égale à 200 °C. Proposer, justification à l’appui, une allure pour la courbe donnant l’évolution de la quantité de matière de phosgène en fonction de la durée t sur le document de l’ANNEXE 1 À RENDRE AVEC LA COPIE (p14/15).

Expérience n°	Quantité de matière des réactifs	Température
1	Mélange réactionnel de 10 mol de CO et 1,0 mol de Cl₂	250°C
2	Mélange réactionnel de 1,0 mol de CO et 1,0 mol de Cl₂	250°C
Cas étudié	Mélange réactionnel de 1,0 mol de CO et 1,0 mol de Cl₂	200°C

Le cas étudié est dans les mêmes conditions de quantité de matière que l’expérience n°2 mais avec une température plus faible.

La température est un facteur cinétique : lorsque la température diminue, la vitesse de réaction diminue également.

Ainsi, la courbe donnant l’évolution de la quantité de matière de phosgène en fonction de la durée t sera en dessous de la courbe de l’expérience 2.

A.3. Le bisphénol A est synthétisé à partir d’acétone et de phénol.

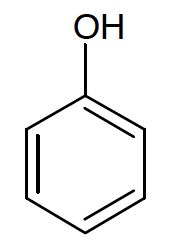
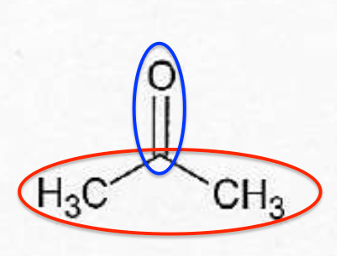
Formule de l’acétone	Formule du phénol

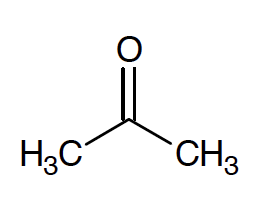A.3.1. Donner le nom de l’acétone en nomenclature systématique.

L’acétone se nomme propanone en nomenclature systématique.

Du phénol C₆H₅OH réagit avec de l’acétone pour former du bisphénol A, C₁₅H₁₆O₂. La réaction modélisant cette transformation est la suivante :

A.3.2. Identifier l’espèce chimique X formée avec le bisphénol A au cours de cette transformation.

Du phénol C₆H₅OH réagit avec de l’acétone pour former du bisphénol A C₁₅H₁₆O₂ et l’espèce chimique X.

	Réactifs		Produits
	2 molécules de phénol C₆H₅OH	1 molécule d’acétone de formule C₃H₆O	1 molécule de bisphénol A C₁₅H₁₆O₂	1 molécule X
Bilan d’atomes	Carbone : $2\times6+3=15$ Oxygène : $2\times1+1=3$ Hydrogène : $2\times(5+1)+6=18$		Carbone : 15 Oxygène : 2 Hydrogène : 16 Sans compter la molécule X

Le nombre d’atome se conserve. Ainsi, la molécule X est constituée de 1 atome d’oxygène et de 2 atomes d’hydrogène.

L’espèce X est l’eau de formule H₂O.

A.3.3. On donne ci-dessous le spectre du bisphénol A. Identifier les liaisons du bisphénol A responsables des bandes d’absorption à 3300 cm^-1 et 2950 cm^-1.

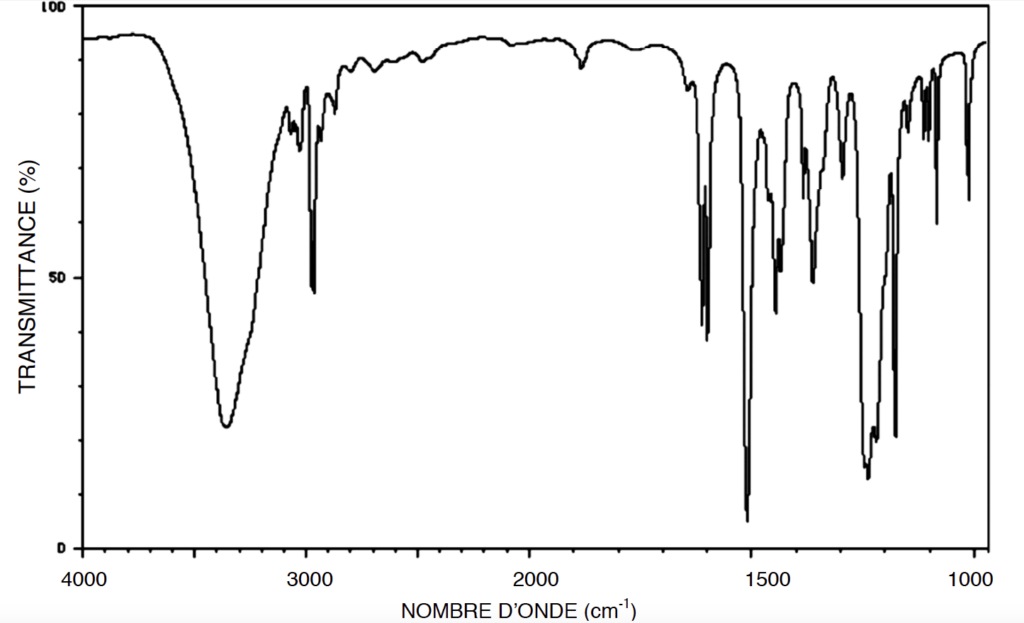
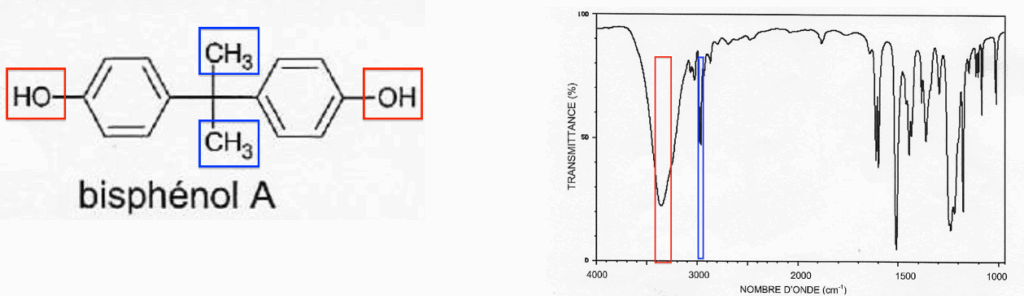
Le bisphénol A possède des liaisons O-H alcool lié responsables de la bande d’absorption à 3300 cm^-1.

Le bisphénol A possède des liaisons C-H responsables de la bande d’absorption à 2950 cm^-1.

Partie B : Réaction de polymérisation

On rappelle l’équation de la réaction modélisant la polymérisation :

Un échantillon de polycarbonate est en réalité un mélange de chaînes polymères de différentes masses molaires. La masse molaire moyenne des macromolécules constituant le polymère vaut M = 30 x 10³ g·mol^-1.

B.1. Déterminer le nombre moyen n de motifs dans une macromolécule.

La masse molaire moyenne des macromolécules constituant le polymère vaut $M=30\times{10}^3\ g.mol^{-1}$.
La masse molaire du motif de polycarbonate de bisphénol A vaut $M_{motif}=254\ g.mol^{-1}$.

$$n=\frac{M}{M_{motif}}$$
$$n=\frac{30\times{10}^3}{254}$$
$$n=118$$

Le nombre moyen $n$ de motifs dans une macromolécule est 118.

Le procédé précédent comporte de nombreux inconvénients parmi lesquels la toxicité du phosgène et l’obtention d’une grande quantité d’eau usée contenant du dichlorométhane et du chlorure de sodium qui doit ensuite être traitée.

Les chimistes ont cherché d’autres procédés moins polluants. Ainsi, d’autres voies de synthèse utilisent du diphénylcarbonate ou « DPC » dans la production de polycarbonate de bisphénol A.

B.2. Une des voies de synthèse du DPC met en jeu l’urée de formule N₂H₄CO, cette dernière étant produite à partir de dioxyde de carbone. Les étapes de la synthèse du DPC sont les suivantes :

CO₂(g) + 2 NH₃(g) → N₂H₄CO(s) + H₂O(g)

La production annuelle d’urée est de de l’ordre de 120 milliards de kilogrammes.

B.2.1. Déterminer la quantité de matière de dioxyde de carbone consommé si l’intégralité de l’urée était préparée par la voie indiquée ci-dessus.

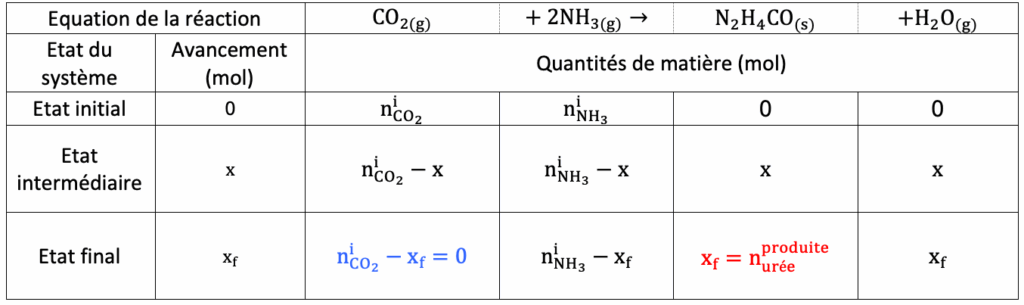
D’après le tableau :
$x_f=n_{urée\ produite}$
$n_{{\rm CO}_2}^i-x_f=0$

D’où
$$n_{{\rm CO}_2}^i=x_f$$
$$n{{\rm CO}_2}^i=n{urée\ produite}$$
$$n_{{\rm CO}_2}^i=m{urée\ produite}/M_{urée}$$
$$n_{{\rm CO}_2}^i=\frac{120 \times {10}^9\times{10}^3}{2 \times 14,0+4 \times 1,0+12,0+16,0}$$
$$n{{\rm CO}_2}^i=2,0 \times {10}^{12}\ mol$$

B.2.2. Un véhicule neuf émet en moyenne 112 g de CO₂ par km et roule en moyenne 13 000 km par an. Déterminer le nombre de véhicules dont l’émission de CO₂ serait compensée par la synthèse de l’urée pour une durée d’un an. Commenter le résultat.

Calculons la masse correspondante :
$$n_{{\rm CO}_2}^i=\frac{m{{\rm CO}_2}}{M{{\rm CO}_2}}$$
$$m{{\rm CO}_2}=n{{\rm CO}_2}^i \times M{{\rm CO}_2}$$
$$m{{\rm CO}_2}=2,0 \times {10}^{12} \times (12,0+2 \times 16,0)$$
$$m{{\rm CO}_2}=9,0 \times {10}^{13}\ g$$

1 km	$112\ g\ de\ {\rm CO}_2$
13 000 km	m

$$m=\frac{13\ 000 \times 112}{1}$$
$$m=1,46\times{10}^6\ g$$

consommés par an pour un véhicule.

1 véhicule	$1,46\times {10}^6\ g\ de\ {\rm CO}_2$
N véhicules	$9,0\times {10}^{13}\ g\ de\ {\rm CO}_2$

$$N=\frac{9,0 \times {10}^{13} \times 1}{1,46 \times {10}^6}$$
$$N=6,2\times{10}^7$$

Le nombre de véhicules dont l’émission serait compensée par la synthèse de l’urée pour une durée de 1 an est de 62 millions.
Ce nombre est non négligeable, cette synthèse permettra de compenser une partie des émissions dues aux véhicules.

ANNEXE 1 À RENDRE AVEC LA COPIE (p14/15)

Questions A.2.4. et A.2.7.

Évolution des quantités de matière de COCl₂ en fonction du temps au cours des expériences 1 et 2