Centres étrangers 2022 Sujet 1
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1G11
Sujet et corrigé
Mots-clés: Schéma de Lewis, réaction acide-base, vitesse volumique, Python
Afin d’améliorer l’interprétation d’une radiographie, des produits de contraste peuvent être administrés aux patients avant l’examen. Ces produits de contraste, non toxiques, une fois éliminés par l’organisme du patient, ne sont pas dégradés par la majorité des stations d’épuration. Pour éviter leur accumulation dans la nature, des chercheurs ont étudié la dégradation des produits de contraste sous l’effet du rayonnement ultraviolet.
Cet exercice traitera dans sa première partie des propriétés chimiques de l’un de ces produits de contraste (l’acide diatrizoïque) puis dans une seconde partie de la cinétique de dégradation de l’acide diatrizoïque et de deux autres produits de contraste (l’acide iotalamique et l’iopamidol) par action d’un rayonnement ultraviolet.
La formule topologique de l’acide diatrizoïque est donnée à la figure 1 ci-dessous.
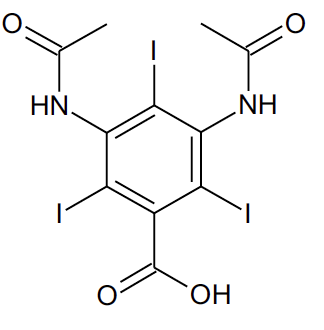
Figure 1. Acide diatrizoïque
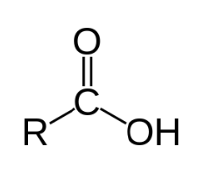
Figure 1 bis. Notation simplifiée de l’acide diatrizoïque
Données :
- Masses molaires atomiques :
| Élément | H | C | O |
| M (g∙mol–1) | 1,00 | 12,0 | 16,0 |
Première partie : propriétés chimiques de l’acide diatrizoïque
1. En utilisant la notation simplifiée de l’acide diatrizoïque, donnée figure 1 bis, représenter le schéma de Lewis de l’acide diatrizoïque et le schéma de Lewis de l’ion carboxylate correspondant.
Schéma de Lewis de l’acide diatrizoique :

Schéma de Lewis de l’ion carboxylate correspondant :
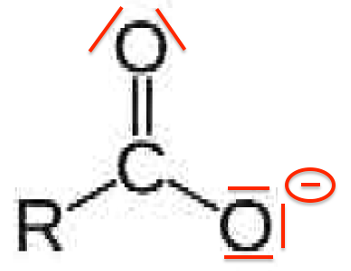
Dans la suite de l’exercice, on utilisera, pour l’acide diatrizoïque et l’ion correspondant, les notations simplifiées RCOOH et RCOO–
2. Établir l’équation de réaction acide-base de l’acide diatrizoïque avec l’eau. Exprimer la constante d’acidité KA du couple acide diatrizoïque / ion diatrizoate en fonction des concentrations à l’équilibre des espèces en solution.
$$RCOOH_{(aq)} + H_2O_{(l)} \rightleftarrows RCOO_{(aq)}^- + H_3O_{(aq)}^+$$
$$K_A = \frac{[RCOO^-]*{eq} \times [H_3O^+]*{eq}}{[RCOOH]_{eq} \times c^0}$$
3. Représenter le diagramme de prédominance du couple de l’acide diatrizoïque et identifier l’espèce prédominante dans les eaux usées.
Données :
- La valeur du pKa du couple acide diatrizoïque / ion diatrizoate est 1,1.
- La valeur du pH des eaux usées est comprise entre 6,5 et 8.
Diagramme de prédominance :

Dans les eaux usées 6,5<pH<8 : pH>pKa . L’espèce prédominante est l’ion carboxylate RCOO–.
Seconde partie : cinétique de dégradation de produits de contraste
Sous l’effet du rayonnement ultraviolet, les produits de contraste sont dégradés. On s’intéresse à la cinétique de dégradation des trois produits de contraste : l’acide diatrizoïque, l’acide iotalamique et l’iopamidol, étudiée dans un article signé par Allard S., Criquet J. et al.
On s’intéresse dans un premier temps à la dégradation des acides diatrizoïque et iotalamique.
La figure 2 suivante représente la variation de concentration des acides diatrizoïque et iotalamique en solution aqueuse en fonction du temps.
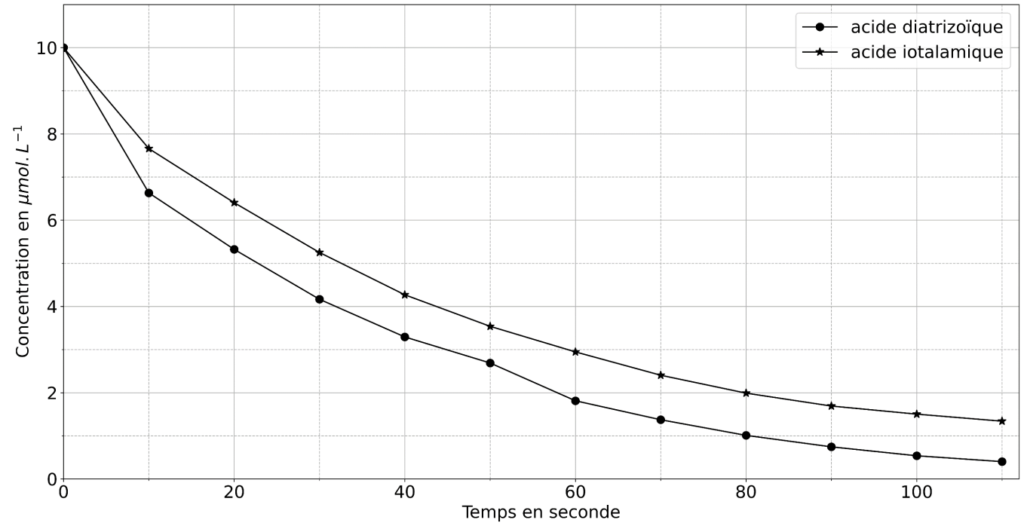
Source : Allard S., Criquet J. et al. Water Research. 2016
4. À l’aide de la figure 2, déterminer les valeurs des temps de demi-réaction pour les deux acides. Identifier le produit de contraste qui se dégrade le plus rapidement.
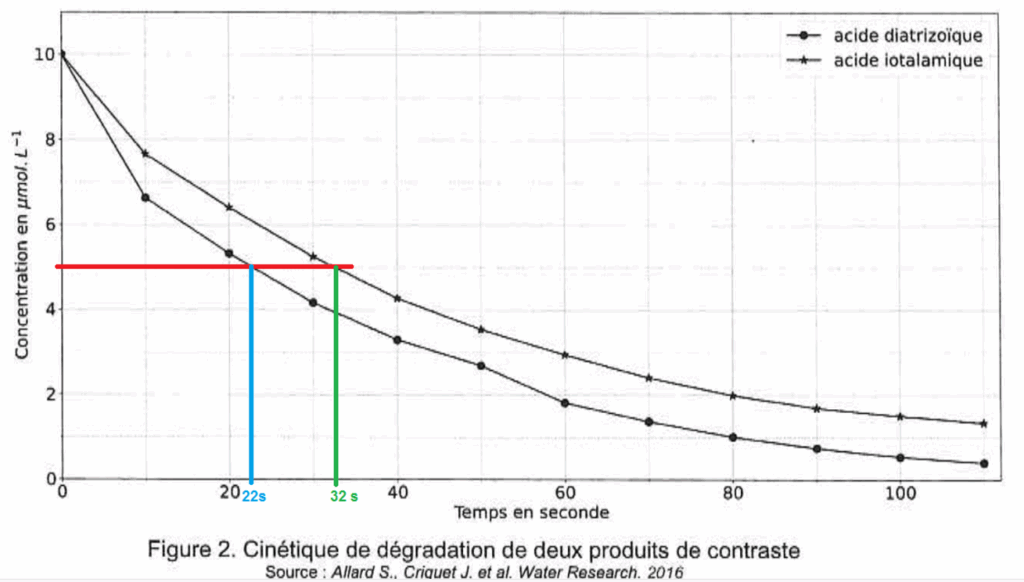
Pour l’acide diatrizoïque $t_{1/2}=22\ s$
Pour l’acide iotalmique $t_{1/2}=32\ s$
Le produit qui se dégrade le plus rapidement est celui qui a le $t_{1/2}$ le plus petit :
l’acide diatrizoïque se dégrade le plus rapidement.
On s’intéresse dans un second temps à la dégradation de l’iopamidol en solution aqueuse. On note [Iop](𝑡) la concentration en iopamidol à la date t.
5. Donner la définition de la vitesse volumique 𝑉 de disparition de l’iopamidol en fonction de sa concentration [Iop](𝑡).
$$v = -\frac{d[Iop]_{(t)}}{dt}$$
Si la cinétique de dégradation est d’ordre 1 alors la vitesse volumique de disparition de l’iopamidol peut s’écrire également : 𝑉 = 𝑘 × [Iop](𝑡) où 𝑘 est une constante positive.
6. En déduire que, dans ce cas, l’évolution temporelle de la concentration peut être modélisée par l’équation différentielle suivante :
$\frac{d[Iop](t)}{dt} +k \times [Iop](t)= 0 $
$$v = -\frac{d[Iop]*{(t)}}{dt}$$
Or, pour une vitesse d’ordre 1 : $v = k \times [Iop]*{(t)}$
D’où :
$$k \times [Iop]*{(t)} = -\frac{d[Iop]*{(t)}}{dt}$$
$$\frac{d[Iop]*{(t)}}{dt} + k \times [Iop]*{(t)} = 0$$
À l’aide d’un programme Python (voir ci-dessous), les données de Allard S., Criquet J. et al. ont été modélisées en utilisant la solution de cette équation différentielle, qui est de la forme :
[Iop](𝑡) = [Iop]0 × 𝑒−(𝑘.𝑡)
Dans cette expression, [Iop]0 est égale à [Iop](𝑡 = 0), concentration en iopamidol à la date 𝑡 = 0.
Programme Python permettant de modéliser les données :
import numpy as np
from scipy.optimize import curve_fit
#Données
temps = np.array([0,10,20,30,40,50,60,70,80,90,100,110])
Iopamidol = np.array([10.0,7.74,6.22,5.24,4.36,3.67,2.98,2.43,1.99,1.66,1.39,1.11])
def func(x, a, b):
return a * np.exp(-b*x) #modèle de notre fonction
#modélisation des données expérimentale par notre fonction
popt, pcov = curve_fit(func, temps, Iopamidol, bounds=(0, [15, 0.1]))
Les valeurs obtenues à l’aide du programme Python sont : a = 9,70 et b = 0,020.
7. À partir des données et de la courbe de modélisation représentée figure 3 ci-dessous, justifier que le modèle de la cinétique d’ordre 1 est validé. Relier les deux paramètres a et b du programme Python aux constantes [Iop]0 et 𝑘.
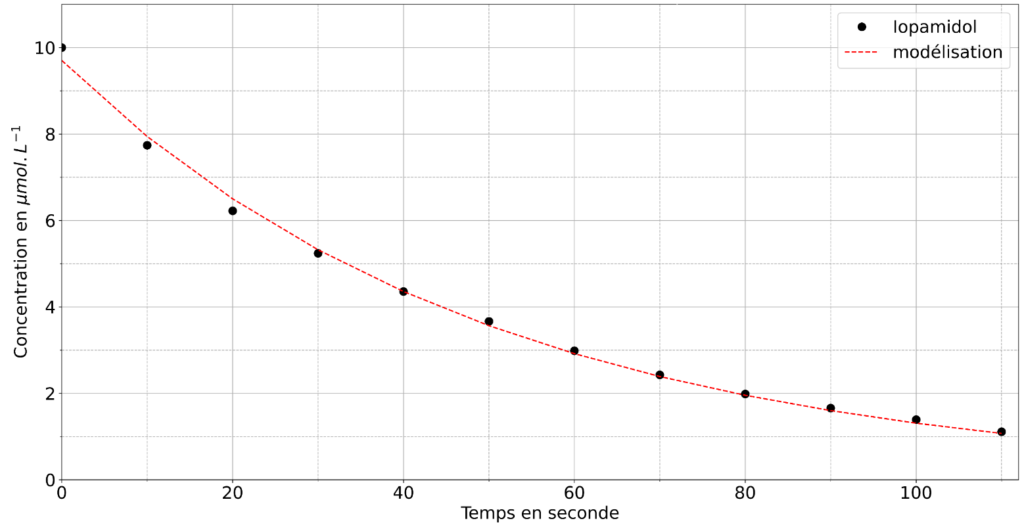
Figure 3 : Graphique représentant les données expérimentales et la modélisation pour une cinétique d’ordre 1
La modélisation représente $[Iop]_{(t)} = [Iop]_0 e^{-kt}$.
Cette fonction est solution de l’équation différentielle pour une cinétique d’ordre 1.
Les points expérimentaux sont sur la courbe de la modélisation.
Ainsi, le modèle de la cinétique d’ordre 1 est validé.
Dans le programme Python :
$[Iop]_{(t)} = a e^{-bt}$
Par identification :
$a = [Iop]_0$
$b = k$
Un établissement de santé souhaite traiter ses eaux usées à l’aide de rayonnement ultraviolet identique à celui utilisé par les chercheurs pour limiter son rejet d’iopamidol. La valeur de la concentration initiale de ses eaux usées en Iopamidol [Iop]0 est de 10,0 µmol∙L–1. Il souhaite ne pas dépasser une concentration en masse de 2,0 mg∙L–1 pour l’eau traitée.
8. En précisant la méthode, déterminer la durée minimum tm nécessaire du traitement.
Donnée : La valeur de la masse molaire de l’iopamidol est égale à 777 g∙mol–1.
$$[Iop]_{(t)} = [Iop]*0 e^{-kt}$$
$$[Iop]*0 e^{-kt} = [Iop]*{(t)}$$
$$e^{-kt} = \frac{[Iop]*{(t)}}{[Iop]*0}$$
$$\ln(e^{-kt}) = \ln\left(\frac{[Iop]*{(t)}}{[Iop]*0}\right)$$
$$-kt = \ln\left(\frac{[Iop]*{(t)}}{[Iop]*0}\right)$$
$$t = \frac{\ln\left(\frac{[Iop]*{(t)}}{[Iop]_0}\right)}{-k}$$
Avec :
$[Iop]*0 = 10,0\times10^{-6}\ mol.L^{-1}$ (concentration molaire)
$[Iop]*{m(t)} = 2,0\times10^{-3}\ g.L^{-1}$ (concentration massique)
$k = b = 0,020\ s^{-1}$
$$c = \frac{n}{V} = \frac{m}{M V} = \frac{c_m}{M}$$
$$[Iop]*{(t)} = \frac{[Iop]*{m(t)}}{M} = \frac{2,0\times10^{-3}}{777} = 2,6\times10^{-6}\ mol.L^{-1}$$
$$t = \frac{\ln\left(\frac{[Iop]_{(t)}}{[Iop]_0}\right)}{-k}$$
$$t_m = \frac{\ln\left(\frac{2,6\times10^{-6}}{10,0\times10^{-6}}\right)}{-0,020}$$
$$t_m = 67\ s$$
La durée minimum nécessaire au traitement est $t_m = 67\ s$.
