Nouvelle Calédonie 2022 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1NC1
Sujet et corrigé
Mots clés de l’EXERCICE B : dissolution, concentration en masse, titrage conductimétrique.
Les eaux souterraines du littoral contenues dans les nappes phréatiques sont essentielles tant pour les activités humaines que pour l’environnement, mais les intrusions d’eau de mer dans ces nappes peuvent engendrer des pollutions irréversibles. Ce risque d’intrusion saline augmente en raison d’une exploitation excessive par pompage des eaux souterraines afin de faire face à une population qui ne cesse d’augmenter sur le littoral.
Ainsi, une surveillance de la qualité des eaux souterraines sur la bordure du littoral est nécessaire afin d’éviter ce risque d’intrusion d’eau saline dans la nappe phréatique.
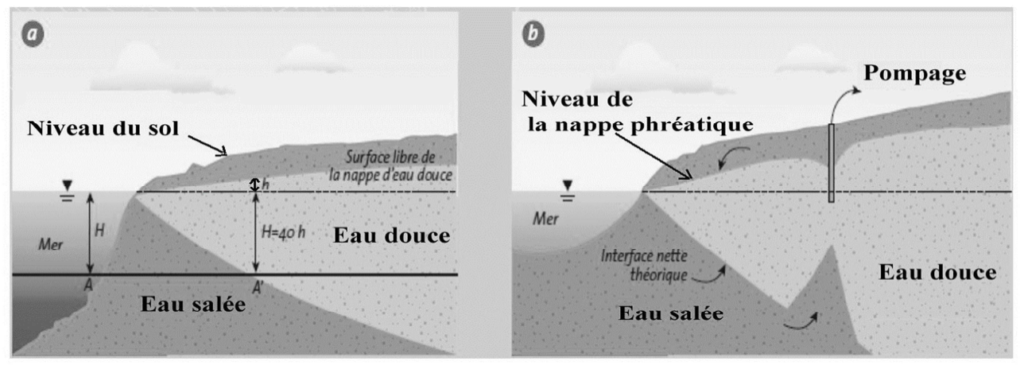
Figure 1 : Lors de l’exploitation d’un forage dans une nappe phréatique côtière, un cône de rabattement se forme au niveau de la surface de la nappe, qui modifie l’interface entre l’eau douce et l’eau salée. Source : d’après https://library.ensh.dz.
L’objectif de cet exercice est de déterminer la concentration en masse en ion chlorure d’un prélèvement d’eau afin de prévenir une éventuelle intrusion d’eau marine dans la nappe souterraine.
A. L’eau salée de la mer Méditerranée
Des classes de concentrations peuvent être définies en fonction des teneurs en ions chlorure :
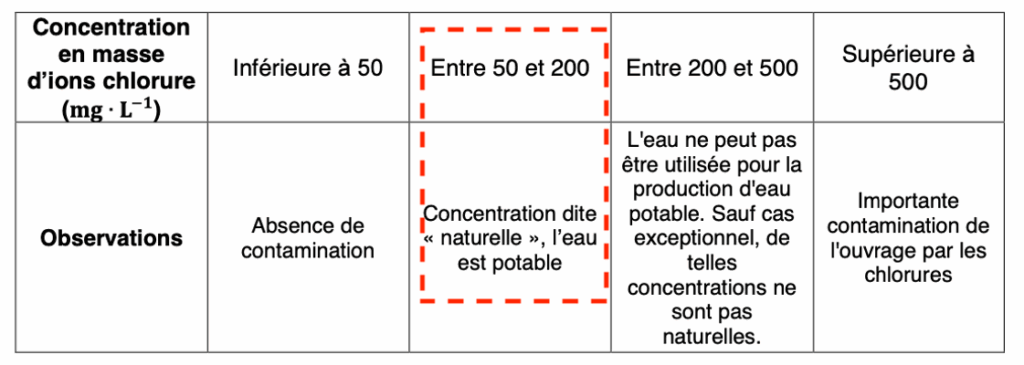
| Concentration en masse d’ions chlorure (mg ∙ L–1) | Inférieure à 50 | Entre 50 et 200 | Entre 200 et 500 | Supérieure à 500 |
| Observations | Absence de contamination | Concentration dite « naturelle », l’eau est potable | L’eau ne peut pas être utilisée pour la production d’eau potable. Sauf cas exceptionnel, de telles concentrations ne sont pas naturelles. | Importante contamination de l’ouvrage par les chlorures |
A.1. Citer la valeur de la concentration minimale en masse cm en ion chlorure Cl–(aq) à partir de laquelle on peut considérer que l’eau souterraine est contaminée par une intrusion d’eau de mer la rendant non potable.
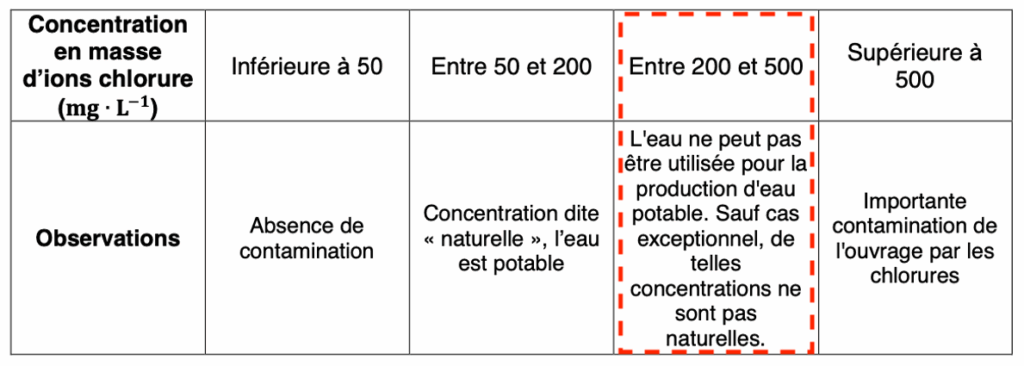
L’eau souterraine est contaminée par une intrusion d’eau de mer la rendant non potable à partir d’une concentration $c_m=200\ mg{.L}^{-1}$
A.2.
Données :
Masses molaires atomiques (en g ∙ mol–1)
| Cl– | Na+ | Mg2+ |
| 35,5 | 23,0 | 24,3 |
Nous allons, dans un premier temps, déterminer la concentration en masse en ion chlorure de l’eau de la mer Méditerranée. La présence des ions chlorure Cl– est principalement due à la dissolution du chlorure de sodium NaCl(s) dans l’eau mais le chlorure de magnésium participe aussi à la salinité de l’eau de mer.
L’équation de la réaction modélisant la dissolution du chlorure de magnésium MgCl2(s) dans l’eau est : MgCl2(s) → Mg2+(aq) + 2 Cl–(aq) .
A.2.1. Sachant que la concentration en quantité de matière de chlorure de magnésium MgCl2(s) dans l’eau de mer vaut c = 4,0 × 10–2 mol ∙ L–1, déterminer la concentration en quantité de matière en ions chlorure Cl–(aq) apportés par MgCl2, notée [Cl–(aq)].
$$\mathrm{MgCl}_{2(s)} \rightarrow \mathrm{Mg}{(aq)}^{2+}+2\ \mathrm{Cl}_{(aq)}^-$$
Ainsi :
$\left[\mathrm{Mg}{(aq)}^{2+}\right]=C=4,0{.10}^{-2}\ mol{.L}^{-1}$
$\left[\mathrm{Cl}{(aq)}^-\right]=2C=2\times 4,0{.10}^{-2}=8,0{.10}^{-2}\ mol{.L}^{-1}$
A.2.2. La concentration en masse en ions chlorure Cl– apportés par le chlorure de sodium NaCl(s) dans l’eau a pour valeur cm = 16,5 g ∙ L–1. Déterminer alors la concentration totale en masse en ions chlorure dans la mer Méditerranée.
$c_{mtotal}=\dfrac{m_{total}}{V}$
$m_{total}=m_1+m_2$
Avec
$m_1$ la masse de $\mathrm{Cl}^-$ provenant du chlorure de magnésium
$m_2$ la masse de $\mathrm{Cl}^-$ provenant du chlorure de sodium
$m_1=n_1\times M_{\mathrm{Cl}^-}$
$m_1=\left[\mathrm{Cl}^-\right]\times V\times M_{\mathrm{Cl}^-}$
$m_2=c_m\times V$
D’où
$c_{mtotal}=\dfrac{m_{total}}{V}$
$c_{mtotal}=\dfrac{m_1+m_2}{V}$
$c_{mtotal}=\dfrac{\left[\mathrm{Cl}^-\right]\times V\times M_{\mathrm{Cl}^-}+c_m\times V}{V}$
$c_{mtotal}=\dfrac{V\times\left(\left[\mathrm{Cl}^-\right]\times M_{\mathrm{Cl}^-}+c_m\right)}{V}$
$c_{mtotal}=\left[\mathrm{Cl}^-\right]\times M_{\mathrm{Cl}^-}+c_m$
$c_{mtotal}=8,0{.10}^{-2}\times 35,5+16,5$
$c_{mtotal}=19,3\ g{.L}^{-1}$
B. Titrage des ions chlorure de l’eau douce des eaux souterraines
La concentration en masse en ions chlorure de l’eau douce qui se trouve proche de la zone de pompage doit être surveillée. Pour cela, un prélèvement d’eau de 50,0 mL est effectué au niveau du pompage.
On titre ensuite les ions chlorure de cette solution d’eau par une solution de nitrate d’argent
(Ag+(aq) + NO3– (aq)) de concentration en quantité de matière 1,00 × 10–2 mol∙L–1.
Le titrage est suivi par conductimétrie. L’équation de la réaction support du titrage est :
Ag+(aq) + Cl–(aq) → AgCl(s)
Données :
Conductivités molaires ioniques à 25°C (S ∙ m2 ∙ mol–1)
| λCl– (aq) | λAg+(aq) | λNO3– (ag) |
| 76,3× 10–4 | 71,4× 10–4 | 61,9× 10–4 |
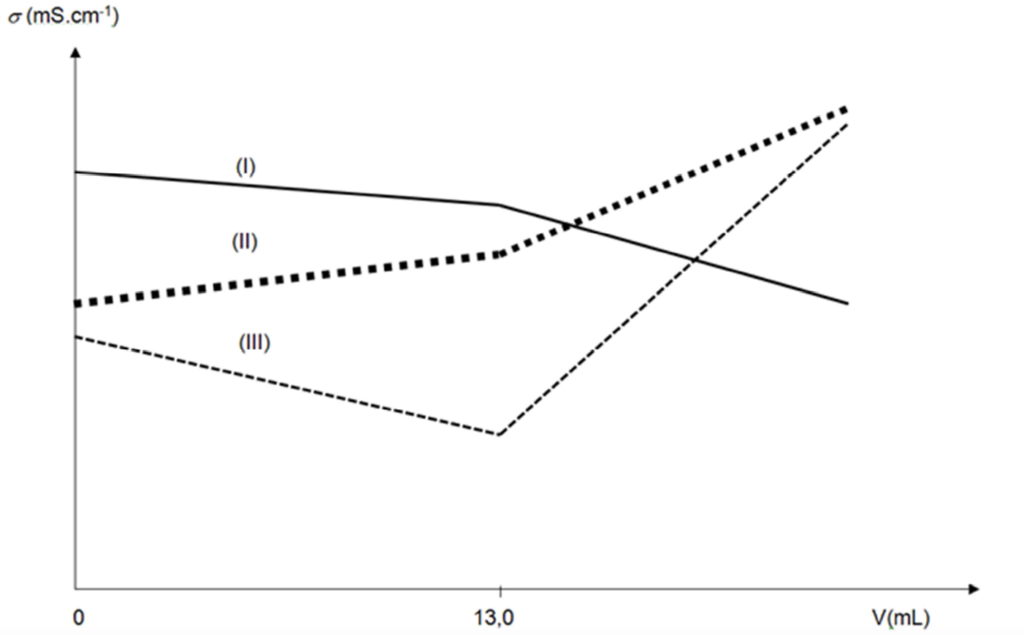
B.1. Identifier, parmi les trois courbes I, II et III proposées sur le graphique de la figure 2 page suivante, celle qui représente l’évolution simulée de la conductivité s du mélange en fonction du volume V de solution de nitrate d’argent versé. Justifier votre réponse.
$$\mathrm{Ag}{(aq)}^++\mathrm{Cl}{(aq)}^-\rightarrow\mathrm{AgCl}_{(s)}$$
Avant l’équivalence :
• les ions $\mathrm{Ag}^+$ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, la concentration des ions $\mathrm{Ag}^+$ est nulle.
• les ions $\mathrm{NO}_3^-$ sont ajoutés, ils ne réagissent pas, la concentration des ions $\mathrm{NO}_3^-$ augmente.
• les ions $\mathrm{Cl}^-$ sont consommés, la concentration des ions $\mathrm{Cl}^-$ diminue.
Donc les ions $\mathrm{Cl}^-$ sont remplacés par des ions $\mathrm{NO}_3^-$.
Or $\lambda{\mathrm{Cl}^-}>\lambda_{\mathrm{NO}_3^-}$ ainsi $\boldsymbol{\sigma}$ diminue avant l’équivalence.
| Ions | Avant l’équivalence |
| $\mathrm{Ag}^+$ | 0 |
| $\mathrm{NO}_3^-$ | ↗ |
| $\mathrm{Cl}^-$ | ↘ |
Après l’équivalence :
• les ions $\mathrm{Ag}^+$ sont ajoutés et ne sont plus consommés, la concentration des ions $\mathrm{Ag}^+$ augmente.
• les ions $\mathrm{NO}_3^-$ sont ajoutés, ils ne réagissent pas, la concentration des ions $\mathrm{NO}_3^-$ augmente.
• les ions $\mathrm{Cl}^-$ n’existent plus, la concentration des ions $\mathrm{Cl}^-$ est nulle.
La concentration des ions augmente, ainsi $\boldsymbol{\sigma}$ augmente après l’équivalence.
| Ions | Après l’équivalence |
| $\mathrm{Ag}^+$ | ↗ |
| $\mathrm{NO}_3^-$ | ↗ |
| $\mathrm{Cl}^-$ | 0 |
La courbe III est celle qui représente l’évolution de la conductivité en fonction du volume $V$ de solution de nitrate d’argent versé.
B.2. Le volume versé à l’équivalence est Veq = 13,0 mL. En déduire si l’eau du prélèvement peut être utilisée pour l’alimentation en eau potable.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
$$\mathrm{Ag}{(aq)}^++\mathrm{Cl}{(aq)}^-\rightarrow\mathrm{AgCl}_{(s)}$$
À l’équivalence :
$$\frac{n_{\mathrm{Cl}^-}^i}{1}=\frac{n_{\mathrm{Ag}^+}^{eq}}{1}$$
$$c\times V=c_{\mathrm{Ag}^+}\times V_{eq}$$
$$c=\frac{c_{\mathrm{Ag}^+}\times V_{eq}}{V}$$
$$c=\frac{1,00{.10}^{-2}\times 13,0{.10}^{-3}}{50,0{.10}^{-3}}$$
$$c=2,60{.10}^{-3}\ mol{.L}^{-1}$$
Calculons la concentration massique $c_m$ :
$$c_m=c\times M$$
$$c_m=2,60{.10}^{-3}\times 35,5$$
$$c_m=9,23{.10}^{-2}\ g{.L}^{-1}$$
$$c_m=92,3\ mg{.L}^{-1}$$
La concentration massique est comprise entre 50 et 200 mg.L$^{-1}$ : l’eau est potable.
L’eau du prélèvement peut donc être utilisée pour l’alimentation en eau potable.
C. Modélisation d’un titrage
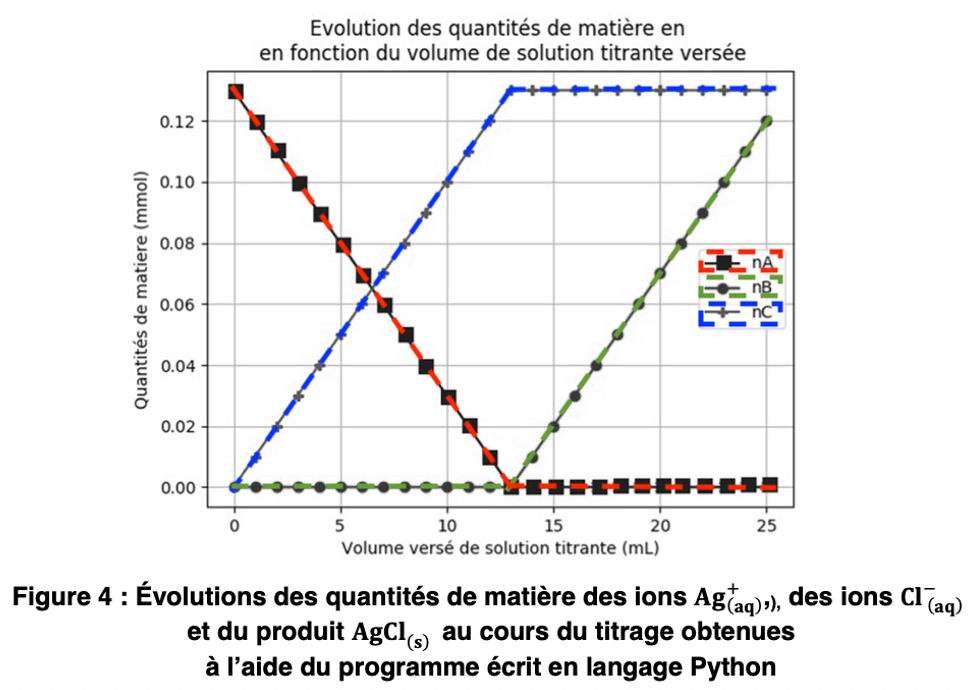
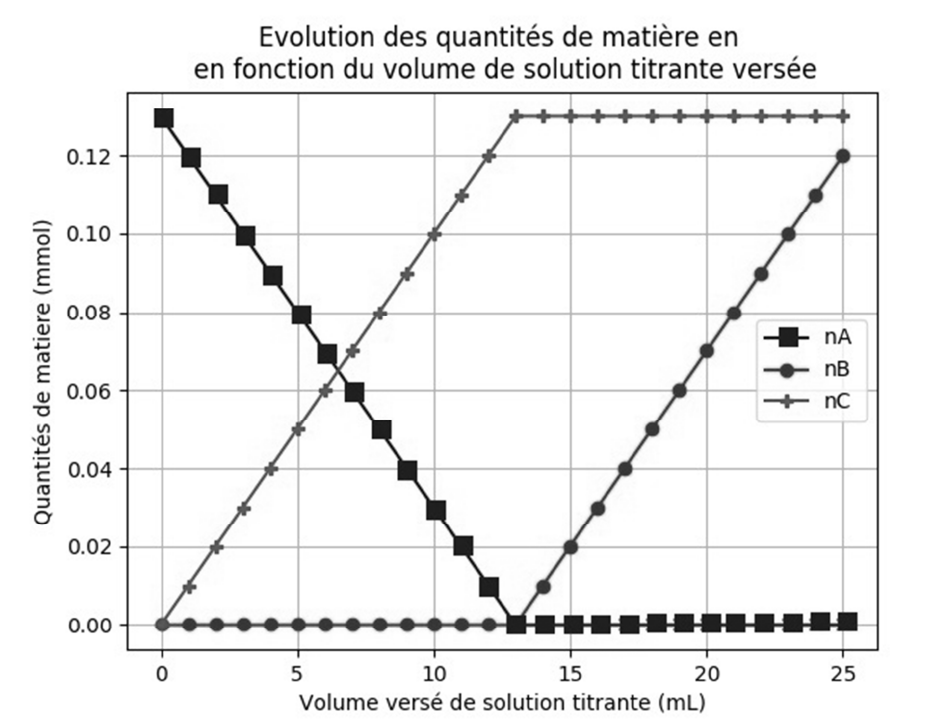
Ce titrage peut être modélisé en utilisant le langage de programmation Python (extrait en figure 3). L’objectif est de visualiser l’évolution des quantités de matière des ions Ag+(aq) , des ions Cl–(aq) et du produit AgCl(s) au cours du titrage (figure 4).
C.1. Les quantités de matière nA, nB et nC, mentionnées et calculées aux lignes 21, 22, 23, 28, 29 et 30 du programme Python (figure 3), sont représentées sur la figure 4. Grâce à cette dernière et avec justification, identifier les espèces chimiques A, B et C.
| Ions | Avant l’équivalence | Après l’équivalence | |
| $\mathrm{Ag}^+$ | 0 | ↗ | nB |
| $\mathrm{NO}_3^-$ | ↗ | ↗ | |
| $\mathrm{Cl}^-$ | ↘ | 0 | nA |
AgCl est un produit : sa quantité de matière augmente avant l’équivalence. Après l’équivalence, il n’y a plus de réaction, sa quantité de matière est constante : $n_C$.
A : $\mathrm{Cl}^-$
B : $\mathrm{Ag}^+$
C : AgCl
C.2. Compléter la ligne 15 du programme python de la figure 3 afin qu’il calcule la concentration en quantité de matière en ions chlorure.
| 1 | import numpy as np |
| 2 | import matplotlib.pyplot as plt |
| 3 | |
| 4 | # Définition des quantités de matière de A, B et C |
| 5 | nA=[] |
| 6 | nB=[] |
| 7 | nC=[] |
| 8 | |
| 9 | # Conditions expérimentales |
| 10 | cB = 0.01 # Saisie de la concentration de la solution titrante (mol/L) |
| 11 | VA = 50 # Saisie du volume initial de solution titrée (mL) |
| 12 | Veq = 13 # Saisie du volume équivalent (mL) |
| 13 | |
| 14 | # Calcul de la concentration en quantité de matière en ions chlorure |
| 15 | cA = ? |
| 16 | print(« Concentration en quantité de matière en ions chlorure = « ,cA, » mol/L ») |
| 17 | |
| 18 | # Calcul des quantités de matière en mmol avant et à l’équivalence |
| 19 | # en fonction du volume V de solution titrante versé |
| 20 | def avant_Eqv(V): |
| 21 | nA.append(cA*VA – cB*V) |
| 22 | nB.append(0) |
| 23 | nC.append(cB*V) |
| 24 | |
| 25 | # Calcul des quantités de matière en mmol après l’équivalence |
| 26 | # en fonction du volume V de solution titrante versé |
| 27 | def apres_Eqv(V): |
| 28 | nA.append(0) |
| 29 | nB.append(cB*V-cA*vA) |
| 30 | nC.append(cA*VA) |
Figure 3 : Extrait du programme écrit en langage Python
D’après la question B.2.
La concentration en ions $\mathrm{Cl}^-$ se calcule avec la relation :
$$c=\frac{c_{\mathrm{Ag}^+}\times V_{eq}}{V}$$
Or dans le programme python :
A : $\mathrm{Cl}^-$
B : $\mathrm{Ag}^+$ On écrira donc dans la ligne 15 :
$$cA=\left(cB\ast Veq\right)/VA$$
