Synthèse d’un biocarburant

Bac Asie 2021 Sujet 1

Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 21-PYCJ1JA1

Mots-clés : synthèse chimique d’un ester.

Le but de cet exercice est d’étudier la synthèse d’un « biocarburant », l’ester méthylique de colza.

La synthèse de ce biocarburant nécessite de l’huile de colza et du méthanol comme réactifs. Elle est modélisée par la réaction d’équation suivante :

C₅₇H₉₈O₆ + 3 CH₃OH → 3 C₁₉H₃₄O₂ + C₃H₈O₃

La formule semi-développée de l’ester méthylique de colza est :

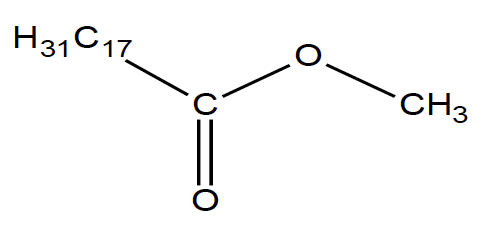
Description d’une synthèse d’ester méthylique de colza réalisée au laboratoire

Matériel et produits

huile de colza commerciale (𝑚₁ = 100,0 g),
méthanol (𝑚₂ = 25,0 g),
solution aqueuse d’hydroxyde de sodium (soude),
solution aqueuse saturée de chlorure d’ammonium,
sulfate de sodium anhydre,
un ballon de 500 mL, trois béchers, une éprouvette graduée de 100 mL,
balance au dixième de gramme,
barreau aimanté,
ampoule à décanter,
dispositif de chauffage à reflux (chauffe-ballon avec agitateur magnétique, réfrigérant à eau et dispositif de fixation).

Étapes du protocole

Mettre l’huile de colza dans le ballon, puis ajouter le méthanol et le catalyseur (soude).
Porter le contenu du ballon à 60 °C et chauffer à reflux pendant une heure environ en homogénéisant à l’aide de l’agitateur magnétique.
Lorsque l’agitation et le chauffage sont arrêtés, deux phases sont visibles. Les séparer par décantation.
La phase organique est récupérée, puis lavée par une solution aqueuse saturée de chlorure d’ammonium et enfin séchée sur du sulfate de sodium anhydre.
Les dernières traces de méthanol sont retirées par évaporation sous une hotte aspirante.
Mesurer la masse et le volume du produit de synthèse obtenu.

Données à 25°C :

Masses molaires atomiques : 𝑀(C) = 12,0 g ⋅ mol⁻¹ ; M(H) = 1,0 g ⋅ mol⁻¹ ; M(O) = 16,0 g ⋅ mol⁻¹.
Masses molaires moléculaires : 𝑀(méthanol) = 32,0 g ⋅ mol⁻¹ ; 𝑀(huile de colza) = 878 g ⋅ mol⁻¹.
Masse volumique du produit synthétisé C₁₉H₃₄O₂ : 𝜌 = 0,880 g ⋅ mL⁻¹.

L’ester méthylique de colza

1. Après avoir recopié la formule semi-développée de l’ester méthylique de colza, entourer le groupe caractéristique présent dans la molécule.

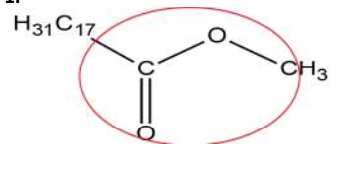
2. Déterminer la masse molaire moléculaire de l’ester méthylique de colza.

$M_{C_{19}H_{34}O_2}=19M_C+34M_H+2M_O$

$M_{C_{19}H_{34}O_2}=19 \times 12,0+34 \times 1,0+2 \times 16,0$

$M_{C_{19}H_{34}O_2}=294\ g.mol^{-1}$

Analyse du protocole de synthèse

3. Identifier, dans le protocole, les conditions opératoires destinées à augmenter la vitesse de synthèse de l’ester méthylique de colza.

Les conditions opératoires destinées à augmenter la vitesse de synthèse de l’ester méthylique de colza sont :

Ajout d’un catalyseur
Augmentation de la température

4. Identifier, dans le protocole de synthèse, les étapes correspondant à la transformation des réactifs, et à la séparation du produit, en les associant aux numéros des étapes du protocole.

Transformation des réactifs : étapes 1 et 2

Séparation du produit : étape 3

Analyse du produit formé

Le produit synthétisé a une masse 𝑚 = 72,9 ± 0,1 g et un volume 𝑉 = 82,0 ± 0,1 mL.

L’incertitude-type u(𝜌) sur la masse volumique 𝜌 se déduit des valeurs et incertitudes sur la masse 𝑚 et le volume 𝑉 par l’expression suivante :

$\left (\frac{u(\rho)}{\rho}\right)^2= \left (\frac{u(m)}{m}\right)^2+\left (\frac{u(V)}{V}\right)^2$

5. Déterminer la valeur de la masse volumique du produit obtenu lors de la synthèse.

$\rho=\frac{m}{V}$

$\rho=\frac{72,9}{82,0}$

$\rho=0,889\ g.{\rm ml}^{-1}$

6. Écrire le résultat de la détermination expérimentale de la masse volumique avec son incertitude associée.

$\left(\frac{u\left(\rho\right)}{\rho}\right)^2=\left(\frac{u(m)}{m}\right)^2+\left(\frac{u(V)}{V}\right)^2$

$u\left(\rho\right)=\rho\sqrt{\left(\frac{u(m)}{m}\right)^2+\left(\frac{u(V)}{V}\right)^2}$

$u\left(\rho\right)=0,889\ \sqrt{\left(\frac{0,1}{72,9}\right)^2+\left(\frac{0.1}{82,0}\right)^2}$

$u\left(\rho\right)=0,002\ g.{\rm ml}^{-1}$

$\rho=0,889\pm0,002\ g.{\rm ml}^{-1}$

7. Comparer le résultat expérimental de la masse volumique avec la valeur de référence du produit synthétisé en utilisant le quotient $\frac{\lvert \rho-\rho_{ref} \rvert}{u(\rho)}}$

$\frac{\left|\rho-\rho_{ref}\right|}{u(\rho)}=\frac{\left|0,889-0,880\right|}{0,002}=4,5$

$\frac{\left|\mathbf{\rho}-\mathbf{\rho}_{\mathbf{ref}}\right|}{\mathbf{u}(\mathbf{\rho})}>\mathbf{2}$

La mesure n’est pas jugée convenable au regard de la référence.

8. Pas de question ( note de l’auteur du site)

Rendement de la synthèse

9. Montrer que le méthanol est le réactif introduit en excès et déterminer la masse maximale d’ester méthylique de colza pouvant être théoriquement obtenue si la transformation est totale et le produit entièrement récupéré.

Quantités de matière des réactifs :

$n_1=\frac{m_1}{M_1}$

$n_1=\frac{100}{878}=1,14{ \times 10}^{-1}\ mol$

$n_2=\frac{m_2}{M_2}$

$n_2=\frac{25,0}{32,0}=7,81{ \times 10}^{-1}\ mol$

Calculons l’avancement maximal :

$1,1{ \times 10}^{-1}-x_{max1}=0$

$x_{max1}=1,14{ \times 10}^{-1}\ mol$

$7,8{1 \times 10}^{-1}-3x_{max2}=0$

$x_{max2}=\frac{7,81{ \times 10}^{-1}}{3}=2,60{ \times 10}^{-1}\ mol$

$x_{max1}<x_{max2}$

Donc $x_{max}=x_{max1}$ , le méthanol est introduit en excès.

Calculons la masse maximale d’ester méthylique de colza pouvant être théoriquement obtenue si la transformation est totale et le produit entièrement récupéré :

$m_{max}=n_{max} \times M_{C_{19}H_{34}O_2}$