Bac Centres étrangers 2021 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2G11
Sujet et corrigé
Mots-clés : évolution temporelle d’un système, loi de vitesse.
Les sodas sont des solutions acides constituées principalement d’eau, de dioxyde de carbone et de saccharose dissous.
Lors de leur fabrication, les industriels indiquent sur l’emballage une date de durabilité minimale (DDM). Après cette date, le produit pourrait ne plus correspondre aux standards de qualité. Pour un soda, la DDM est généralement de 3 mois.

Source : Wikimedia Commons
Un soda acheté depuis longtemps est moins « riche en bulles » mais ce n’est pas la seule altération constatable.
En effet, le saccharose subit, en milieu acide, une hydrolyse qui est une transformation totale conduisant à la formation de deux autres sucres, le glucose et le fructose, modélisée par la réaction d’équation :
C12H22O11(aq) + H2O(ℓ) → C6H12O6(aq) + C6H12O6(aq)
saccharose S glucose fructose
Le mélange de glucose et de fructose a un pouvoir sucrant différent de celui du saccharose d’où une modification de la saveur sucrée de la boisson.
La problématique de cet exercice est de déterminer le pourcentage de saccharose restant dans la boisson lorsque la DDM est atteinte.
On réalise en laboratoire la réaction d’hydrolyse du saccharose à une température constante de 20°C et dans une solution tampon fixant le pH à 2,5.
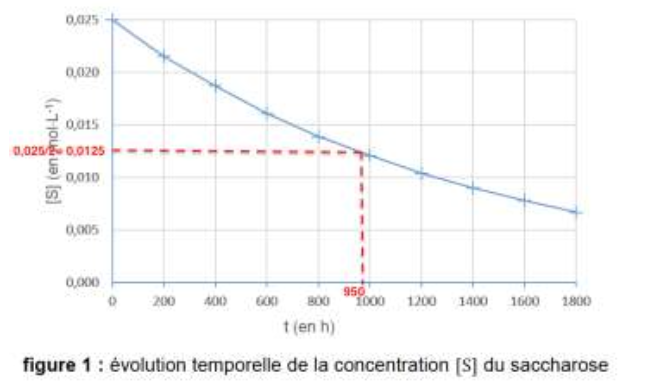
On effectue un suivi de la réaction par une méthode physique pour déterminer la concentration en saccharose, notée [S]. L’évolution temporelle de la concentration en saccharose est représentée en figure 1 (page 8/16).
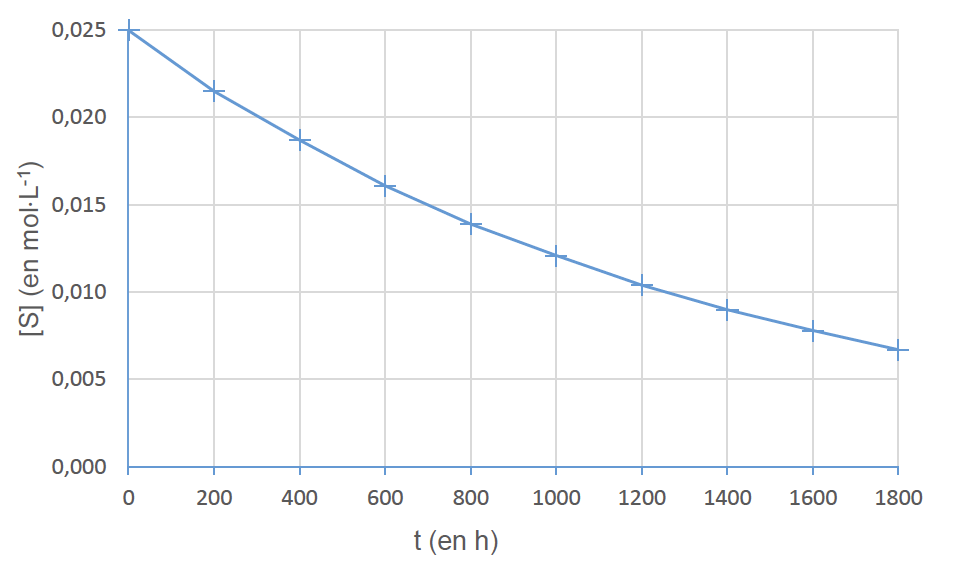
1. Proposer une justification de l’utilisation d’une solution tampon de pH inférieur à 7 pour réaliser cette expérience.
D’après le texte : « le saccharose subit, en milieu acide, une hydrolyse qui est une transformation totale conduisant à la formation de deux autres sucres,… »
Ainsi la solution doit avoir un pH<7 pour subir cette transformation.
De plus, une solution tampon est une solution qui maintient approximativement le même pH malgré l’addition de petites quantités d’un acide ou d’une base, ou malgré une dilution.
Nous utilisons dans cette expérience une solution tampon afin que la solution reste acide pendant toute l’expérience.
2. Expliquer pourquoi les mesures effectuées ne permettent pas de répondre directement à la problématique.
Calculons 3 mois en heures : $3 \times 30 \times 24=2160\ h$
Or le graphique s’arête pour 1800h, c’est pourquoi les mesures effectuées ne permettent pas de répondre directement à la problématique
Pour pouvoir estimer le pourcentage de saccharose restant lorsque la DDM est atteinte, on souhaite modéliser l’évolution temporelle de sa concentration [S]. On émet l’hypothèse que cette évolution suit une loi de vitesse d’ordre 1 et on souhaite vérifier cette hypothèse.
3. Définir la vitesse volumique v de disparition du saccharose.
$$v_d=-\frac{d\left[S\right]_{(t)}}{dt}$$
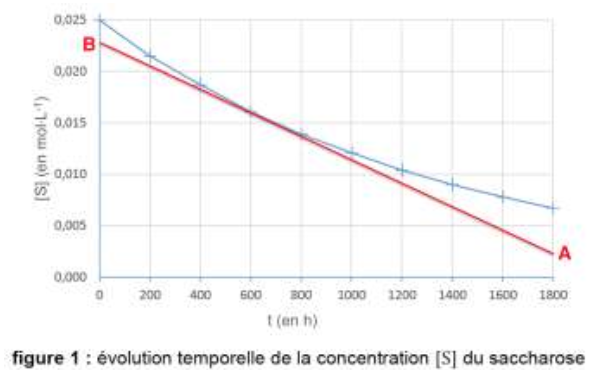
4. Expliquer comment obtenir une estimation de la valeur de la vitesse volumique de disparition du saccharose à un instant t donné à partir des mesures réalisées.
L’explication peut être illustrée par la réalisation de cette estimation pour une date au choix du candidat.
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
Par exemple pour t=600h :
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{0,023-0,0025}{0-1800}=-1,1.{10}^{-5}mol.L^{-1}.h^{-1}$$
$$v_{t=600h}=-\frac{d\left[S\right]_{(t)}}{dt}=-k$$
$$v_{t=600h}=1,1.{10}^{-5}mol.L^{-1}.h^{-1}$$
5. Dans le cas d’une loi de vitesse d’ordre 1, rappeler la relation existant entre la vitesse volumique de disparition v du saccharose, la concentration en saccharose [S] et une constante de vitesse notée 𝑘.
Dans le cas d’une loi de vitesse d’ordre 1, la relation existante entre la vitesse volumique de disparition v du saccharose, la concentration en saccharose [S] et une constante de vitesse notée k est :
$$v_d=k \times \left[S\right]_{(t)}$$
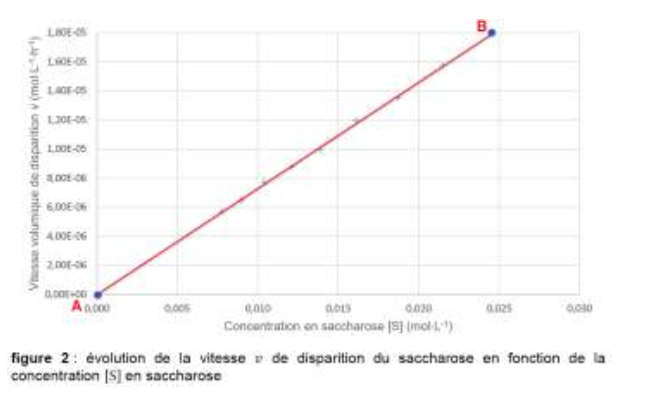
Sur le graphique de la figure 2 (page 9/16), l’évolution de la vitesse volumique v de disparition du saccharose est représentée en fonction de la concentration en saccharose [S].
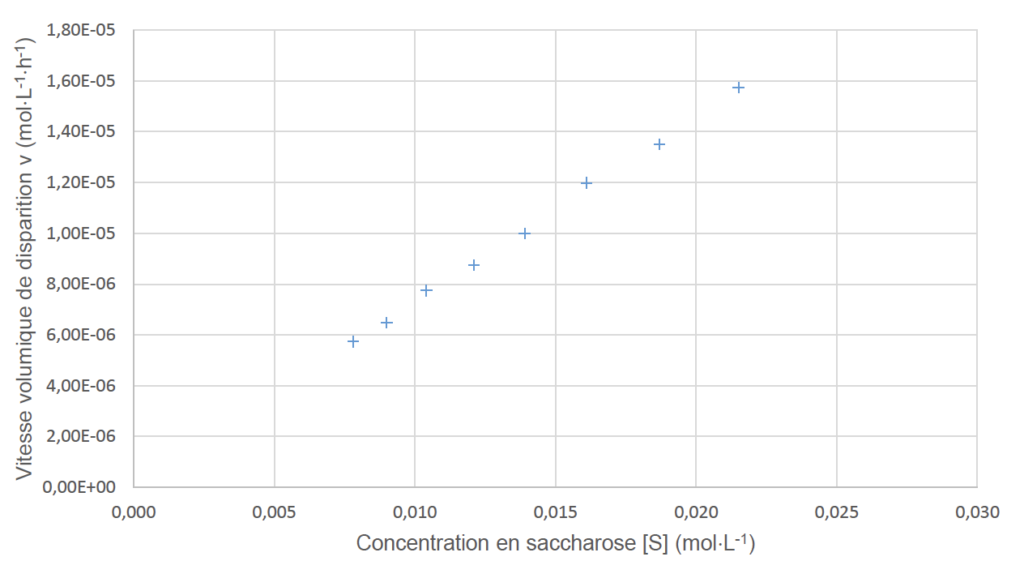
6. Discuter de l’accord des mesures avec une loi de vitesse d’ordre 1.
Nous avons une droite qui passe par l’origine donc vd est proportionnel à $\left[S\right]_{(t)} : \ v_d=k \times \left[S\right]_{(t)}$
C’est bien en accord avec une loi de vitesse d’ordre 1.
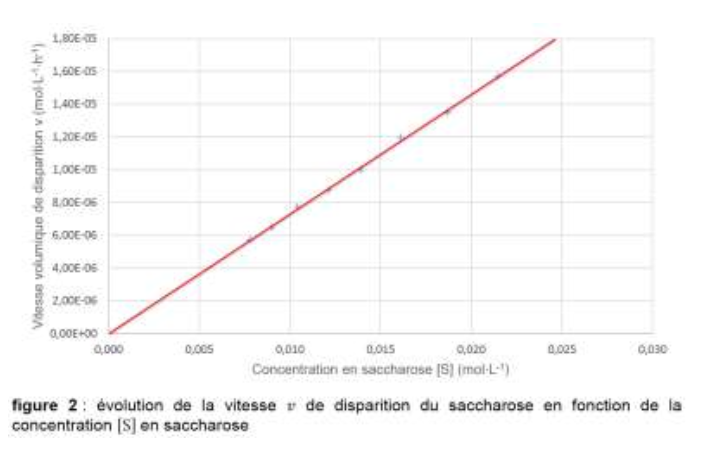
7. Montrer que la constante de vitesse 𝑘 a une valeur de l’ordre de 7,3 ⋅ 10−4 h−1.
K est le coefficient directeur de la droite :
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{1,80.{10}^{-5}-0}{0,0245-0}$$
$$k=7,3.{10}^{-4}h^{-1}$$
L’évolution de la concentration en saccharose s’écrit : [S] = [S]0 e−𝑘𝑡
[S]0 désigne la concentration initiale en saccharose.
8. Rappeler la définition du temps de demi-réaction noté t1/2 et montrer que, pour cette loi d’évolution, le temps de demi-réaction a la propriété d’être indépendant de la concentration initiale en saccharose.
t1/2 est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : x(t1/2) = xf/2.
$$\left[S\right]_{\left(t=t_{1/2}\right)}=\left[S\right]_i{ \times e}^{-k \times t_{1/2}}$$
or $$\left[S\right]_{\left(t=t_{1/2}\right)}=\frac{\left[S\right]_i}{2}$$
Donc $$\left[S\right]_i{ \times e}^{-k \times t_{1/2}}=\frac{\left[S\right]_i}{2}$$
$$e^{-k \times t_{1/2}}=\frac{1}{2}$$
$${ln(e}^{-k \times t_{1/2}})=\ln\funcapply(\frac{1}{2})$$
$$-k \times t_{1/2}=-\ln\funcapply(2)$$
$$t_{1/2}=\frac{\ln{\left(2\right)}}{k}$$
Le temps de demi-réaction est donc indépendant de la concentration initiale en saccharose.
9. Déterminer la valeur du temps de demi-réaction dans les conditions de l’expérience. Expliquer la démarche suivie.
Dans les conditions de l’expérience :
$$\left[S\right]_{\left(t=t_{1/2}\right)}=\frac{\left[S\right]_i}{2}=\frac{0,025}{2}=0,0125\ mol.L^{-1}$$
Par lecture graphique : t1/2=950 h.
Non demandé :
par calcul $$t_{1/2}=\frac{\ln{\left(2\right)}}{k}=\frac{\ln{\left(2\right)}}{7,3.{10}^{-4}}=950\ h$$
10. Estimer le pourcentage de saccharose restant dans le soda lorsque la DDM de 3 mois est atteinte.
Le candidat est invité à présenter sa démarche même si elle n’est pas complètement aboutie.
$$\left[S\right]_{\left(t=3mois\right)}=\left[S\right]_i{ \times e}^{-k \times t_{3\ mois}}$$
$$P=\frac{\left[S\right]_{\left(t=3mois\right)}}{\left[S\right]_i} \times 100=\frac{\left[S\right]_i{ \times e}^{-k \times t_{3\ mois}}}{\left[S\right]_i} \times 100=e^{-k \times t_{3\ mois}} \times 100$$
$$P=e^{-7,3.{10}^{-4} \times 3 \times 30 \times 24} \times 100$$
P=20%
Lorsque la DDM de 3 mois est atteinte, le pourcentage de saccharose restant dans le soda est de 20%.
