Bac Métropole Septembre 2021 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2ME3
Sujet et corrigé
Mots-clés : dosage par étalonnage ; cinétique chimique

L’encre bleue utilisée dans les stylos-plume contient, entre autres, du bleu d’aniline qui contribue à sa couleur. C’est cette couleur qui doit disparaître lors de l’utilisation d’un effaceur.
Dans un premier temps, l’objectif de l’exercice est l’étude du bleu d’aniline, la détermination de sa masse dans une cartouche d’encre, et dans un second temps, l’étude de la vitesse de disparition de l’encre lorsqu’on efface.
Pour simplifier, on note, dans la suite de l’exercice, le bleu d’aniline (2 Na+(aq) ; HBleu2–(aq)). On suppose que seuls les ions HBleu2–(aq) sont responsables de la couleur de l’encre.
Données :
- masses molaires en g·mol–1 :
| hydrogène | oxygène | sodium | soufre | bleu d’aniline |
| 1,0 | 16,0 | 23,0 | 32,0 | 737,7 |
- couple oxydant / réducteur associé au bleu d’aniline : HBleu2–(aq) / H3Bleu2–(aq) ;
- couple oxydant / réducteur hydrogénosulfate / hydrogénosulfite : HSO4–(aq) / HSO3–(aq) ;
- les solutions aqueuses d’ions H3Bleu2–(aq), HSO4–(aq) et HSO3–(aq) sont incolores.
1. Le bleu d’aniline.
Pour caractériser la couleur du bleu d’aniline d’une cartouche d’encre, on vide intégralement une cartouche d’encre dans une fiole jaugée de 200,0 mL et on complète avec de l’eau distillée jusqu’au trait de jauge. On obtient la solution Sencre dont on réalise le spectre grâce à un spectrophotomètre qui est représenté figure 3.
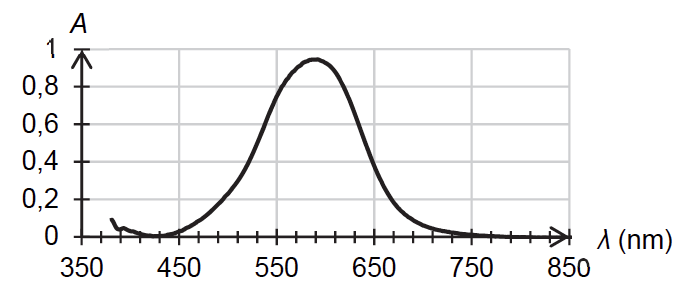
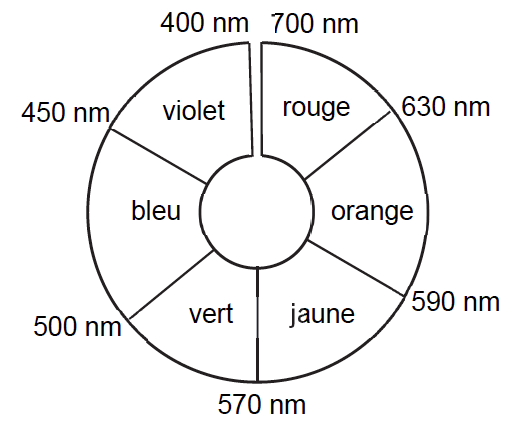
1.1. Justifier la couleur de la solution Sencre.
La couleur absorbée correspond à $\lambda_{max}=590\ nm$ couleur jaune-orange.
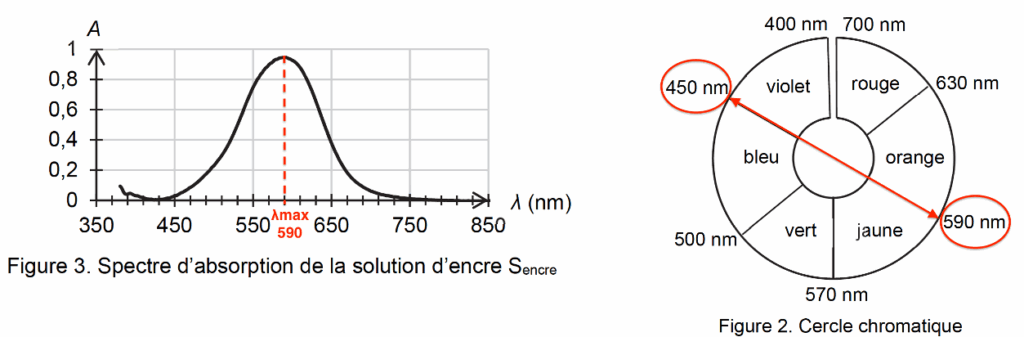
Sa couleur est la couleur complémentaire du jaune-orange (couleur opposée sur le cercle chromatique) : le violet-bleu.
La solution est donc de couleur violet-bleu.
Pour déterminer la masse en bleu d’aniline dans la cartouche d’encre dans la solution Sencre, on réalise une solution mère S0 à une concentration en bleu d’aniline de c0 = 6,78×10–4 mol·L–1.
À partir de la solution mère S0, on réalise plusieurs solutions filles :
| S1 | S2 | S3 | S4 | S5 | |
| Volume prélevé de la solution mère V0 (mL) | 10,0 | 20,0 | 25,0 | 33,0 | 50,0 |
| Volume de la solution fille Vf (mL) | 100,0 | 100,0 | 100,0 | 100,0 | 100,0 |
| Concentration en quantité de matière de la solution fille cf (mol·L–1) | 6,78×10–5 | … | 1,69×10–4 | 2,34×10–4 | 3,39×10–4 |
| Absorbance | 0,322 | 0,584 | 0,882 | 1,195 | 1,489 |
1.2. Nommer la verrerie nécessaire pour réaliser la solution fille S1.
$V_0=10,0\ mL$, le volume de la solution mère est prélevé à l’aide d’une pipette jaugée de 10,0 mL.
$V_1=100,0\ mL$, le volume de la solution fille est celui d’une fiole jaugée de 100,0 mL.
1.3. Déterminer la valeur de la concentration en quantité de matière de la solution fille S2 manquante dans le tableau de valeurs.
Lors d’une dilution, la quantité de matière se conserve :
$n_0=n_2$
$$C_0V_0=C_2V_2$$
$$C_2=\frac{C_0V_0}{V_2}$$
$$C_2=\frac{6,78{.10}^{-4}\times20}{100}$$
$$C_2=1,36{.10}^{-4}\ mol.L^{-1}$$
On représente l’absorbance des différentes solutions filles en fonction de la concentration en bleu d’aniline, mesurée à la longueur d’onde λ= 590 nm retenue pour l’étude.
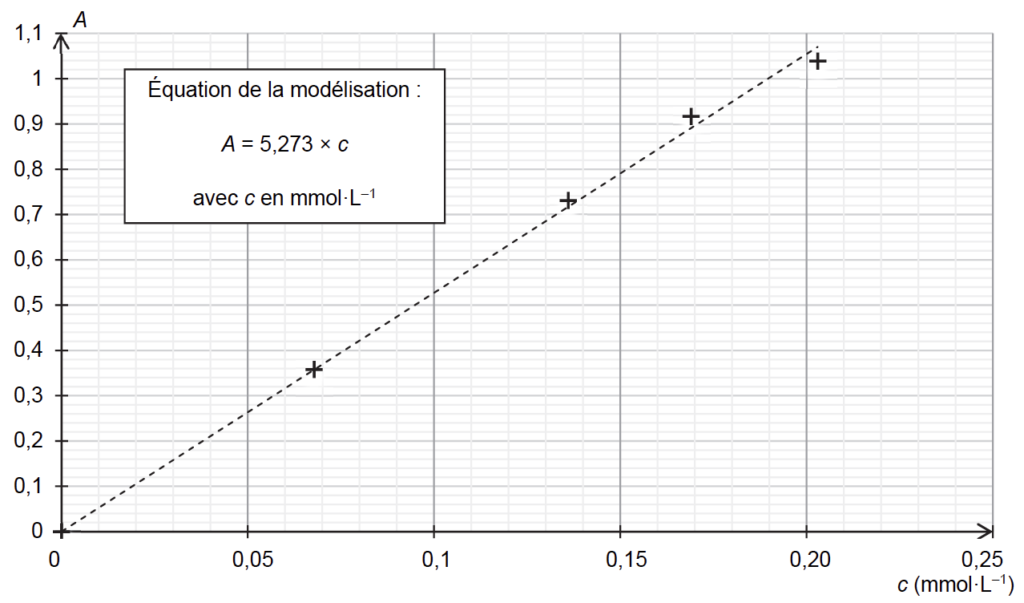
1.4. À la longueur d’onde retenue pour l’étude, l’absorbance de la solution Sencre est égale à 0,9. Déterminer la masse de bleu d’aniline contenue dans une cartouche d’encre.
D’après l’équation de la modélisation : $A=5,273\times C$
Déterminons $C$ :
$$A=5,273\times C$$
$$C=\frac{A}{5,273}$$
$$C=\frac{0,9}{5,273}=0,17\ mmol.L^{-1}$$
Déterminons la masse $m$ :
$m=n\times M$
Or
$n=C\times V$
$$m=C\times V\times M$$
$$m=0,17{.10}^{-3}\times200{.10}^{-3}\times737,7$$
$$m=2,5{.10}^{-2}\ g$$
2. Étude de l’effacement de l’encre
L’effaceur d’encre contient une solution d’hydrogénosulfite de sodium qui réagit avec le bleu d’aniline. On souhaite étudier la transformation qui a lieu lorsqu’on efface l’encre à l’aide de l’effaceur.
2.1. Établir l’équation de la réaction modélisant la transformation entre les ions HSO3–(aq) et les ions HBleu2–(aq).
$$H{\rm Bleu}{(aq)}^{2-}/H_3{\rm Bleu}{(aq)}^{2-} : H{\rm Bleu}{(aq)}^{2-}+2H^++2e^-=H_3{\rm Bleu}{(aq)}^{2-}$$
$$H{\rm SO}{4(aq)}^-/H{\rm SO}{3(aq)}^- : H{\rm SO}{3(aq)}^-+H_2O=H{\rm SO}{4(aq)}^-+2H^++2e^-$$
$$H{\rm Bleu}{(aq)}^{2-}+2H^++H{\rm SO}{3(aq)}^-+H_2O\rlhar H_3{\rm Bleu}{(aq)}^{2-}+H{\rm SO}{4(aq)}^-+2H^+$$
$$H{\rm Bleu}{(aq)}^{2-}+H{\rm SO}{3(aq)}^-+H_2O\rlhar H_3{\rm Bleu}{(aq)}^{2-}+H{\rm SO}{4(aq)}^-$$
2.2. Justifier l’utilité de la présence dans l’effaceur d’une solution contenant des ions hydrogénosulfite.
Ions hydrogénosulfite : $H{\rm SO}{3(aq)}^-$
Les ions hydrogénosulfite réagissent avec $H{\rm Bleu}{(aq)}^{2-}$ qui est responsable de la couleur de l’encre.
Les produits créés $H_3{\rm Bleu}{(aq)}^{2-}+H{\rm SO}{4(aq)}^-$ sont incolores.
Ainsi, la présence d’ions hydrogénosulfite dans l’effaceur permet d’effacer l’encre.
Pour étudier la cinétique de cette transformation, on réalise le protocole suivant :
- on prépare 100,0 mL d’une solution d’encre en mettant 5 gouttes d’encre qu’on dilue dans une fiole jaugée que l’on complète avec de l’eau ;
- on mélange 4 mL de la solution d’encre avec 1 mL de solution aqueuse d’hydrogénosulfite de sodium de concentration 9,0×10–2 mol·L–1 ;
- on suit l’évolution de l’absorbance de la solution Smélange obtenue en fonction du temps (figure 5).
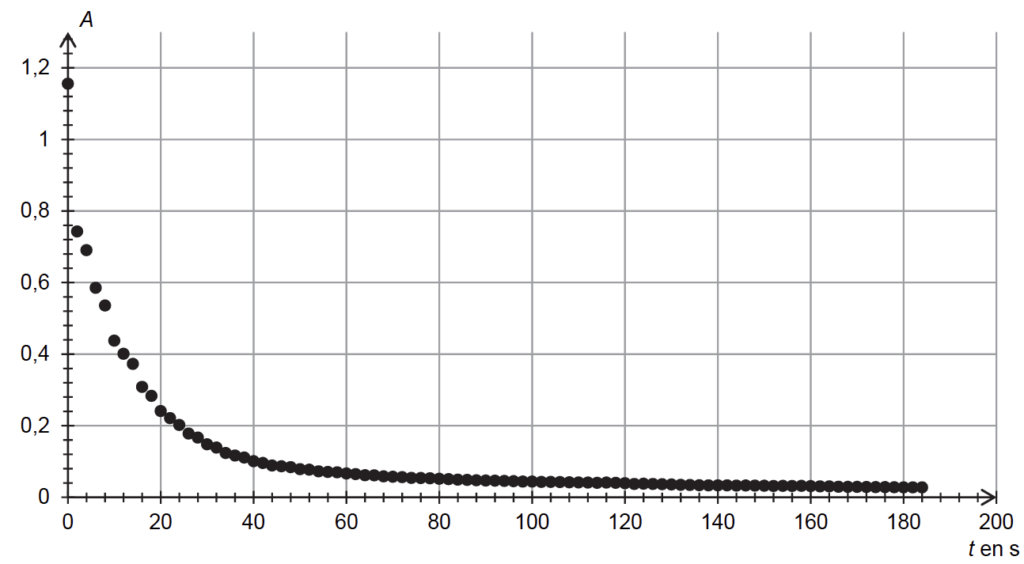
2.3. Une cartouche d’encre de 0,75 mL contient 25 mg de bleu d’aniline. Sachant que 20 gouttes d’encre ont un volume de 1 mL, déterminer le réactif limitant de la transformation. Commenter.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée. Cette question est indépendante de la suite de l’étude.
Trouvons le volume correspondant à 5 gouttes :
| 20 gouttes | 1mL |
| 5 gouttes | $V=\frac{5\times1}{20}=0,25\ mL$ |
Trouvons la masse de bleu d’aniline correspondant à 5 gouttes soit 0,25 mL :
| 0,75 mL | 25 mg |
| 0,25 mL | $m=\frac{0,25\times25}{0,75}=8,33\ mg$ |
8,33 mg sont contenus dans 100 mL. Or on utilise 4 mL de cette solution d’encre :
| 100 mL de solution d’encre | 8,33 mg |
| 4 mL | $m=\frac{4\times8,33}{100}=0,33\ mg$ |
Calculons la quantité de matière correspondante :
$$n_{H{\rm Bleu}^{2-}}=\frac{m_{H{\rm Bleu}^{2-}}}{M_{H{\rm Bleu}^{2-}}}$$
$$n_{H{\rm Bleu}^{2-}}=\frac{0,33{.10}^{-3}}{737,7}$$
$$n_{H{\rm Bleu}^{2-}}=4,5{.10}^{-7}\ mol$$
Calculons la quantité de matière d’ions hydrogénosulfite :
$$n_{H{\rm SO}3^-}=C\times V$$
$$n{H{\rm SO}3^-}=9,0{.10}^{-2}\times1{.10}^{-3}$$
$$n{H{\rm SO}_3^-}=9,0{.10}^{-5}\ mol$$
Trouvons le réactif limitant :
$$x_{max1}=\frac{n_{H{\rm Bleu}^{2-}}}{1}=4,5{.10}^{-7}\ mol$$
$$x_{max2}=\frac{n_{H{\rm SO}3^-}}{1}=9,0{.10}^{-5}\ mol$$
$$x_{max1}<x_{max2}$$
$H{\rm Bleu}^{2-}$ est le réactif limitant.
Le résultat est conforme aux attentes : l’effaceur doit effacer toute l’encre, $H{\rm Bleu}^{2-}$ doit constituer le réactif limitant.
2.4. Estimer le temps de demi-réaction. Commenter le résultat.
$A_0=1,16$
Pour trouver $t_{1/2}$, on cherche $A_{(t=t_{1/2})}=\frac{A_0}{2}=0,58$
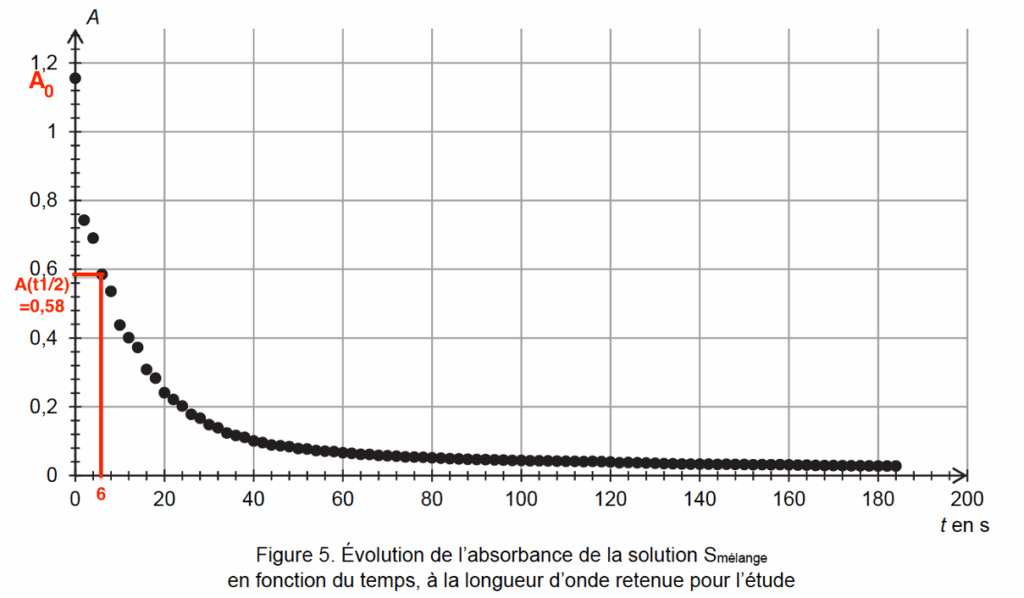
Graphiquement : $t_{1/2}=6\ s$.
Lorsqu’on efface de l’encre avec un effaceur, celle-ci disparaît rapidement. Le temps de réaction $t=5t_{1/2}=30\ s$ est supérieur à nos attentes.
