Bouquet final

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Dans cet exercice, on s’intéresse à différents aspects physico-chimiques d’un feu d’artifice.

La pyrotechnie, du grec « pyros » feu et « teckhnê » savoir-faire, est la technique des feux d’artifice. Elle fut inventée par les chinois, il y a plus de mille ans, et introduite en Occident grâce à Marco Polo au XIII^ème siècle.

Lors d’un feu d’artifice, la pièce d’artifice est l’élément le plus utilisé (voir schéma en coupe figure 1). La pièce est expulsée depuis un mortier jusqu’à une centaine de mètres de haut où elle explose pour former une figure lumineuse. La poudre noire présente dans la pièce d’artifice est un mélange intervenant lors des deux étapes : la propulsion, puis la dispersion des étoiles incandescentes qui forment le feu d’artifice.

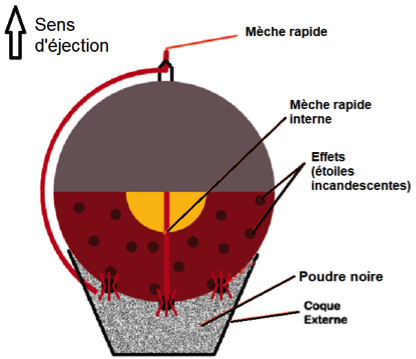
Figure 1 : Coupe d’une pièce d’artifice

Projet Scientifique Collectif « Combustion, flammes et feux d’artifice » École Polytechnique http://www.penangol.fr/rapports/combustion.pdf

Article « Feux d’artifice » du site de la société chimique de France http://www.societechimiquedefrance.fr/feux-d-artifice.html

Données :

– Intensité du champ de pesanteur : g = 9,81 m·s^-2.

– Masses molaires atomiques (en g·mol^-1) : C : 12,0 ; N : 14,0 ; O : 16,0 ; K : 39,1

– Constante de Planck : h = 6,63 × 10^-34 Js ;

– 1 eV = 1,60×10^-19 J ;

– la valeur de la célérité de la lumière c dans le vide est supposée connue par le candidat.

I. Aspect énergétique d’une pièce d’artifice lors de la phase ascensionnelle,

Dans cette partie, on modélise la pièce d’artifice par un point matériel dans le référentiel terrestre supposé galiléen. La pièce d’artifice étudiée, de masse 100 g, est tirée verticalement avec une vitesse initiale de valeur v₀ = 100 m·s^-1. On étudie le mouvement de son centre d’inertie G, repéré par son ordonnée y dans un repère vertical (O, ) orienté vers le haut.

On choisit l’instant t₀ = 0 s lorsque le centre d’inertie G est confondu avec l’origine du repère O. On néglige toute action mécanique de l’air. On admet que la masse de la bombe est constante lors de son mouvement ascendant.

En tenant compte des choix de modélisation précédents, un logiciel de simulation permet de représenter l’évolution temporelle de l’énergie cinétique E_cet de l’énergie potentielle de pesanteur E_p de la bombe lors de son mouvement ascendant : on obtient la représentation graphique ci-dessous.

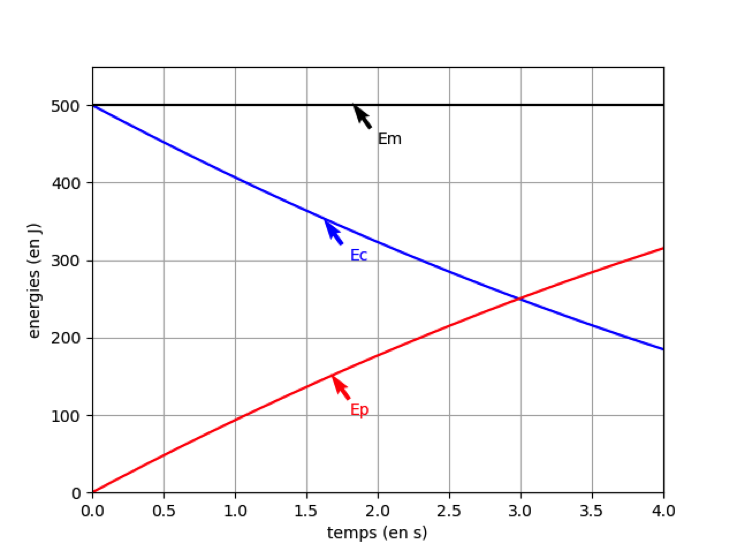
Figure 2 : Évolution des énergies cinétique et potentielle pendant l’ascension de la pièce

1. Après avoir rappelé la définition de l’énergie mécanique de la pièce d’artifice, exploiter la figure 2 pour savoir si, dans la situation simulée, l’énergie mécanique se conserve. Commenter le résultat obtenu.

L’énergie mécanique E_M=E_C+E_p. L’énergie mécanique est la somme des énergies cinétique et potentielle

L’énergie mécanique (courbe noire) ne varie pas lors du mouvement elle se conserve : Em=constante. Ainsi les forces de frottements sont négligeables

2. On suppose que la pièce explose à l’instant t_A= 2,0 s. Après cet instant, les évolutions de la figure 2 ne sont plus respectées. À l’aide de la figure 2, déterminer la valeur de l’énergie potentielle à cet instant puis calculer l’altitude atteinte notée y_A.

Par lecture graphique, pour t=2s , Epp=185J

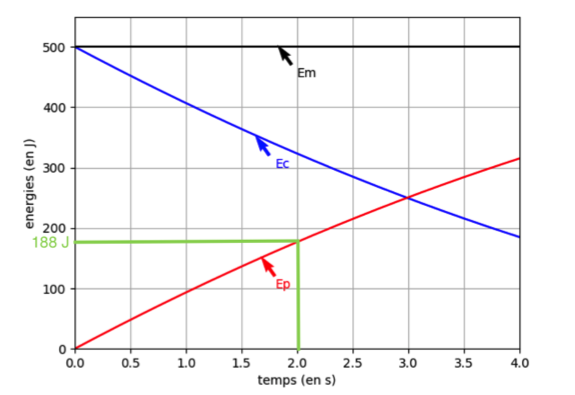
$E_{pp}=m \times g \times Y_{A}$

$Y_{A}=\frac {E_{pp}} {m \times g}$

$Y_{A}=\frac {185} {100.10^{-3}\times 9,81}=188 m$

3. En réalité l’altitude maximale atteinte par la pièce vaut 55 m. Commenter l’écart observé par rapport au modèle.

D’après la question 2, Après cet instant (t=2,0s), les évolutions de la figure 2 ne sont plus : respectées. L’énergie mécanique ne se conserve plus. Ainsi il faut prendre en compte les pertes énergétiques dues aux forces de frottements.

II. Combustion pyrotechnique

Le principe de base des feux d’artifice repose sur la combustion de la poudre noire contenant jusqu’à 75 % en masse de salpêtre de formule KNO₃, jouant le rôle de comburant et un mélange essentiellement constitué de carbone, mais contenant également du soufre et des éléments métalliques pour la couleur (solides ioniques comportant, par exemple, des ions sodium pour le jaune ou des ions potassium pour le violet) ou pour les effets spéciaux (métaux comme par exemple le magnésium pour des étincelles).

Source : http://www.societechimiquedefrance.fr/feux-d-artifice.html

Afin de simplifier cette étude, on fait l’hypothèse que la combustion de la poudre noire peut être modélisée par une seule réaction chimique dont l’équation est :

2 KNO₃ + 3 C + S → K₂S + 3 CO₂ + N₂

4. Après avoir écrit la demi-équation électronique du couple CO₂ / C, préciser si le carbone joue le rôle d’oxydant ou de réducteur.

CO₂ +4H⁺+4e^–= C + 2H₂O

Le carbone est un réducteur car il est capable de céder des électrons.

L’artificier prépare environ 25 g de poudre noire. Ce mélange est réalisé dans les proportions stœchiométriques de la réaction : il contient 3,20 g de carbone, du nitrate de potassium (salpêtre) de formule KNO₃, du soufre S et des solides ioniques ou métaux en faible quantité.

5. Déterminer la valeur de quantité de matière de carbone dans ce mélange.

$n_C=\frac{m_C}{M_C}=\frac{3,20}{12,0}=2,67.10^{-1}mol$

6. En déduire la masse de nitrate de potassium nécessaire pour réaliser ce mélange.

2 KNO₃ + 3 C + S → K₂S + 3 CO₂ + N₂

Il faut que les réactifs soient dans les proportions steochiometrique :

$\frac {n_{KNO_3}} {2}=\frac {n_C} {3}$

$n_{KNO_3}=\frac {2 \times n_C} {3}$

$n_{KNO_3}=\frac{m_{KNO_3}}{M_{KNO_3}}$

$m_{KNO_3}={n_{KNO_3}}\times{M_{KNO_3}}$

$m_{KNO_3}=\frac {2 \times n_C} {3}\times{M_{KNO_3}}$

$m_{KNO_3}=\frac {2 \times 2,67.10^{-1}} {3}\times{(39,1+14,0+3\times 16,0)}}=18,0 g$

7. En déduire le pourcentage massique de nitrate de potassium présent dans la poudre noire préparée et indiquer si le résultat est compatible avec la description de la poudre noire.

D’après le texte : « poudre noire contenant jusqu’à 75 % en masse de salpêtre de formule KNO₃ ». Le résultat est proche de la valeur attendue.

$P_{KNO_3}=\frac{m_{KNO_3}}{m_{totale}}\times 100$

$P_{KNO_3}=\frac{18,0}{25}\times 100=72\%$

Calculons l’écart relatif :

$écart relatif=\frac{P_{KNO_3}-P_{ref}}{P_{ref}}$

$écart relatif= \displaystyle\left\lvert \frac{72-75}{75} \right\rvert =0,04=4\%$

L’écart est inferieur à 5% le résultat est compatible avec la description de la poudre noire.

8. Dans les conditions de la combustion étudiée, l’énergie molaire de combustion (pour la combustion d’une mole de carbone) vaut E_mcomb = – 208 kJmol^-1. Montrer que la valeur de l’énergie libérée par la combustion de la poudre noire préparée par l’artificier est de l’ordre de 55 kJ.

L’énergie libérée lors d’une réaction est proportionnelle à la quantité de matière de combustible consommé :

E=n. E_mcomb

E=2,67.10^-1×-208=-55,5kJ

Le résultat négatif nous indique que l’énergie est libérée.

9. Comparer la valeur précédente à l’énergie cinétique initiale de la bombe (voir figure 2) et interpréter la différence.

Sur la figure 2 on relève Ec_initiale=500J=0,5kJ

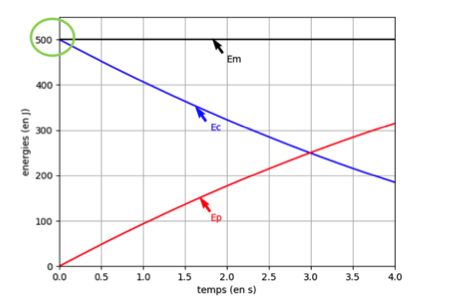
L’énergie libérée est dissipée sous forme thermique (chaleur de la combustion) et seulement une petite partie se converti sous forme d’énergie cinétique

III. Émission lumineuse

Les feux d’artifice émettent de la lumière selon trois phénomènes : l’incandescence, l’émission atomique et l’émission moléculaire. On s’intéresse uniquement à l’émission atomique dans cette partie. Les ions des cristaux métalliques introduits sont excités thermiquement, ce qui leur permet de passer d’un niveau d’énergie fondamental à un niveau d’énergie supérieur ; au cours de leur retour vers l’état fondamental, l’énergie qu’ils avaient absorbée est émise sous forme de photons d’une longueur d’onde caractéristique de l’élément correspondant. L’ion sodium est l’un de ceux qui émet le plus de lumière par ce mécanisme. On donne ci-dessous des informations concernant l’émission de lumière par le sodium.

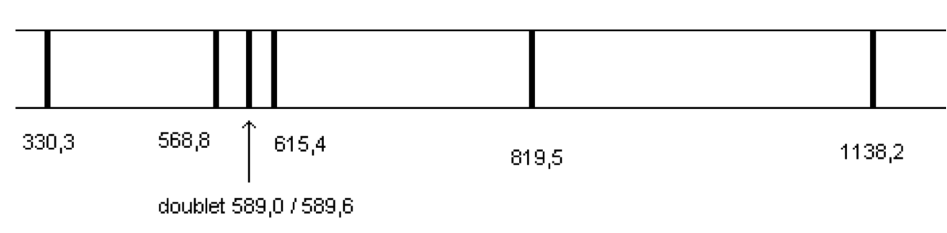
Figure 3 : Longueurs d’onde dans le vide (en nm) du spectre d’émission d’une lampe à vapeurs de sodium

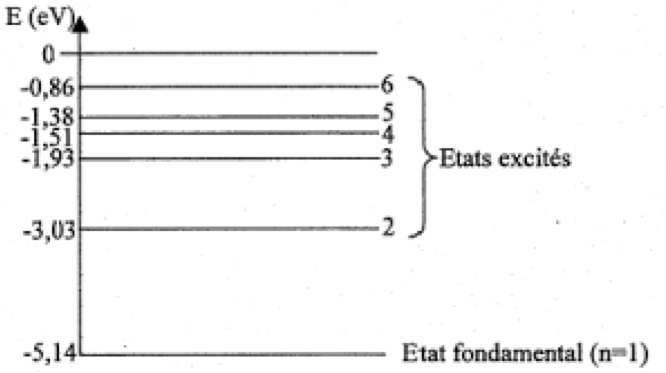
Figure 4 : Diagramme des niveaux d’énergie du sodium

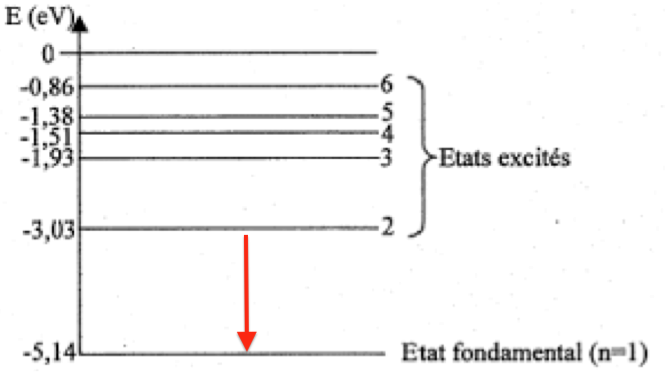
10. Sur un diagramme de niveaux d’énergie d’un atome, comportant le niveau fondamental et un niveau excité d’énergie supérieure, illustrer le phénomène d’émission d’un photon.

Quand un atome transite vers un niveau d’énergie inferieur, un photon est émis.

11. Déterminer quelle transition entre niveaux d’énergie du sodium représentés figure 4 a lieu lors de l’émission de la raie jaune du sodium, de longueur d’onde λ = 589,0 nm dans le vide.
L’élève est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti.

$\Delta E=\lvert \ E_f-E_i\rvert=h \times \nu =h\times \frac{c}{\lambda}$

$\Delta E=\lvert \ E_f-E_i\rvert=6,63.10^{-34}\times \frac{3,00.10^{8}}{589.10^{-9}}=3,37.10^{-19}J$

$\Delta E=\lvert \ E_f-E_i\rvert=2,11 ev}$

Il faut donc trouver un écart entre deux niveaux de 2,11 ev.

Cela correspond au passage du niveau 2 au niveau 1 :

$\left|E_f-E_i\right|=\left|-5,14-(-3,03)\right|=2,11\ ev$