Arôme de vanille

Liban 2022 Sujet 2

Exercice A – (5 points) –  au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ2LR1

[latexpage]

Mots-clés : couples acide/base; titrage par suivi conductimétrique; spectre UV-visible

La vanilline est le constituant principal de l’essence de vanille. Elle est extraite de gousses de vanille séchées et fermentées.

On se propose dans cet exercice de déterminer la masse de vanilline présente dans un arôme alimentaire de vanille Bourbon. Pour cela, on commence par préparer une solution de référence dont on détermine la concentration en vanilline par titrage suivi par conductimétrie. Cette solution de référence est ensuite utilisée pour réaliser un dosage par étalonnage utilisant la spectrophotométrie.

Données :

• masse molaire de la vanilline : 152 g·mol^–1 ;
• conductivités ioniques molaires :

Ion	H3O+	HO–	Cl–	Na+	Vanillinate (V–)
λ0 (mS·m2·mol–1)	35	20	7,6	5,0	Inconnue

1. Préparation d’une solution de référence

On réalise la dissolution d’une faible quantité de vanilline commerciale, dans une solution aqueuse basique d’hydroxyde de sodium. On obtient une solution, notée S1. Dans cette solution S1, la vanilline, notée VH, a réagi avec les ions hydroxyde pour former l’ion vanillinate, noté V^–. L’équation de la réaction modélisant cette transformation chimique est la suivante :

1.1. Écrire la formule brute de la vanilline.

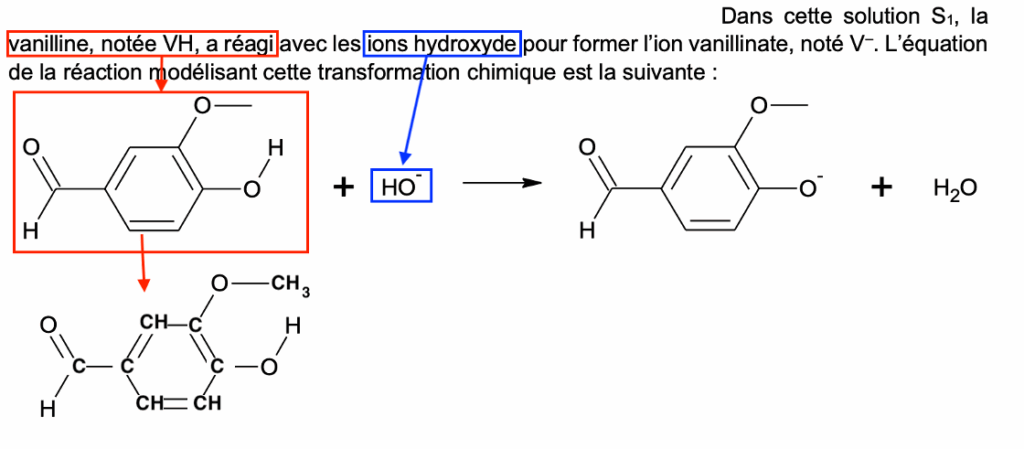
Formule brute de la vanilline : $C_8H_8O_3$.

1.2. Identifier les deux couples acide/base mis en jeu lors de cette réaction.

Les deux couples acide/base :

• $VH/V^-$ (ou $C_8H_8O_3/C_8H_7O_3^-$)
• $H_2O/HO^-$

2. Titrage de la solution de référence S₁

On réalise le titrage d’un volume V₁ = 20,0 mL de solution S₁, auquel on ajoute environ 150 mL d’eau distillée, par de l’acide chlorhydrique de concentration C_a = 1,0×10^–1 mol·L^–1. Le titrage est suivi par conductimétrie.

On obtient la courbe de suivi du titrage suivante :

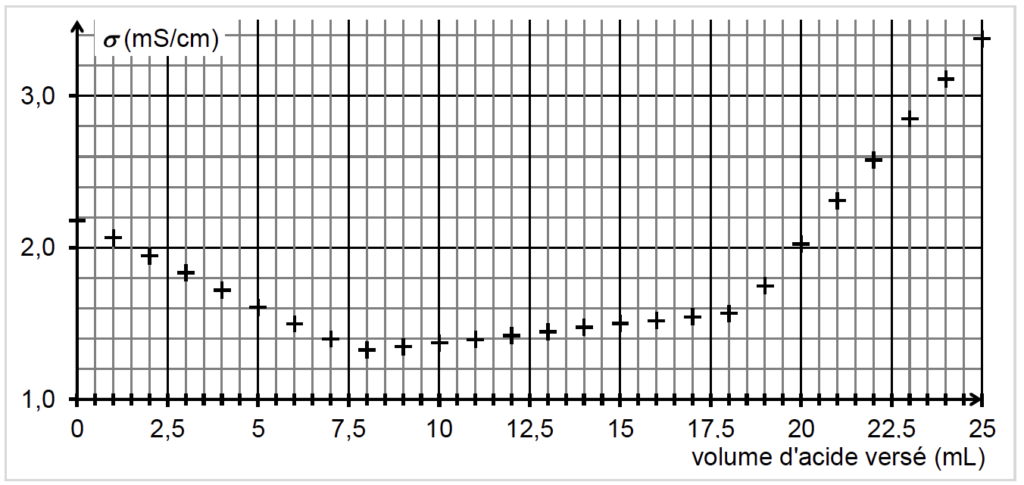
Cette courbe fait apparaitre trois phases distinctes :

• première phase : titrage de l’excès des ions hydroxyde ;
• deuxième phase : titrage de la base conjuguée de la vanilline ;
• troisième phase : ajout d’acide en excès dans le milieu.

Première phase du titrage

2.1. Écrire l’équation de la réaction support du titrage qui a lieu lors de la première phase.

« Première phase : titrage de l’excès des ions hydroxyde »

$${\rm HO}*{(aq)}^-+{H_3O}*{(aq)}^+\rightarrow 2H_2O_{(l)}$$

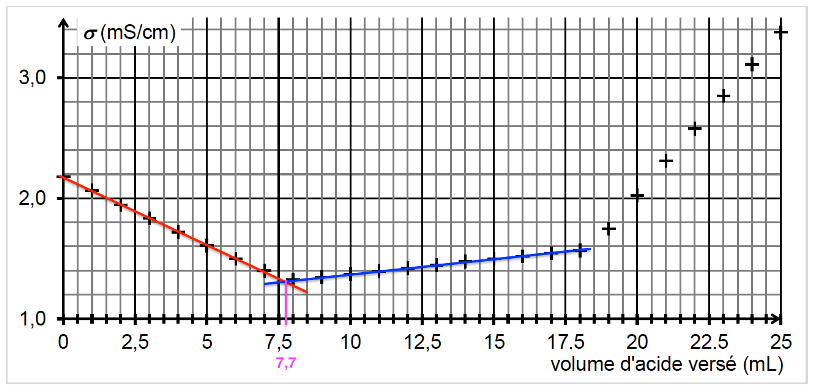
2.2. Déterminer graphiquement le volume d’acide nécessaire au titrage des ions hydroxyde.

2.3. Justifier la pente de la courbe lors de cette première phase.

« Première phase : titrage de l’excès des ions hydroxyde par de l’acide chlorhydrique $({H_3O}_{(aq)}^+;{Cl}_{(aq)}^-)$ »

$${\rm HO}_{(aq)}^-+{H_3O}_{(aq)}^+\rightarrow 2H_2O_{(l)}$$

Ions	Première phase
$HO^-$	↘
$H_3O^+$	0
${\rm Cl}^-$	↗
${\rm Na}^+$	=
$V^-$	=

• Les ions $HO^-$ sont consommés, leur concentration diminue.
• Les ions $H_3O^+$ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, leur concentration est nulle.
• Les ions ${\rm Cl}^-$ sont ajoutés, ne réagissent pas, leur concentration augmente.
• Les ions ${\rm Na}^+$ présents dans l’hydroxyde de sodium ne réagissent pas, leur concentration ne change pas.
• Les ions $V^-$ présents dans la solution ne réagissent pas, leur concentration ne change pas.

Donc les ions $HO^-$ sont remplacés par des ions ${\rm Cl}^-$.

Or $\lambda_{HO^-}>\lambda_{{\rm Cl}^-}$, ainsi $\mathbf{\sigma}$ diminue lors de la première phase.

Deuxième phase du titrage

L’équation de la réaction support du deuxième titrage peut s’écrire :

V^–(aq) + H₃O⁺(aq) → VH(aq) + H₂O(ℓ)

2.4. D’après l’allure de la courbe dans cette deuxième phase du titrage, indiquer si la conductivité ionique molaire de l’ion vanillinate (V^–) est inférieure, supérieure ou égale à celle des ions chlorure. Justifier.

« Deuxième phase : titrage de la base conjuguée de la vanilline par de l’acide chlorhydrique $({H_3O}_{(aq)}^+;{\rm Cl}_{(aq)}^-)$ »

$$V_{(aq)}^-+{H_3O}_{(aq)}^+\rightarrow{\rm VH}_{(aq)}+H_2O_{(l)}$$

Ions	Première phase
$HO^-$	0
$H_3O^+$	0
${\rm Cl}^-$	↗
${\rm Na}^+$	=
$V^-$	↘

• Les ions $HO^-$ n’existent plus, leur concentration est nulle.
• Les ions $H_3O^+$ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, leur concentration est nulle.
• Les ions ${\rm Cl}^-$ sont ajoutés, ne réagissent pas, leur concentration augmente.
• Les ions ${\rm Na}^+$ ne réagissent pas, leur concentration ne change pas.
• Les ions $V^-$ réagissent, leur concentration diminue.

Donc les ions $V^-$ sont remplacés par des ions ${\rm Cl}^-$.

Or $\mathbf{\sigma}$ augmente donc lors de cette deuxième phase.

Donc $\lambda_{V^-}<\lambda_{{\rm Cl}^-}$.

La conductivité ionique molaire de l’ion vanillinate $(V^-)$ est inférieure à celle des ions chlorure.

2.5. Déterminer le volume d’acide nécessaire au seul titrage de l’ion vanillinate, en explicitant votre démarche.

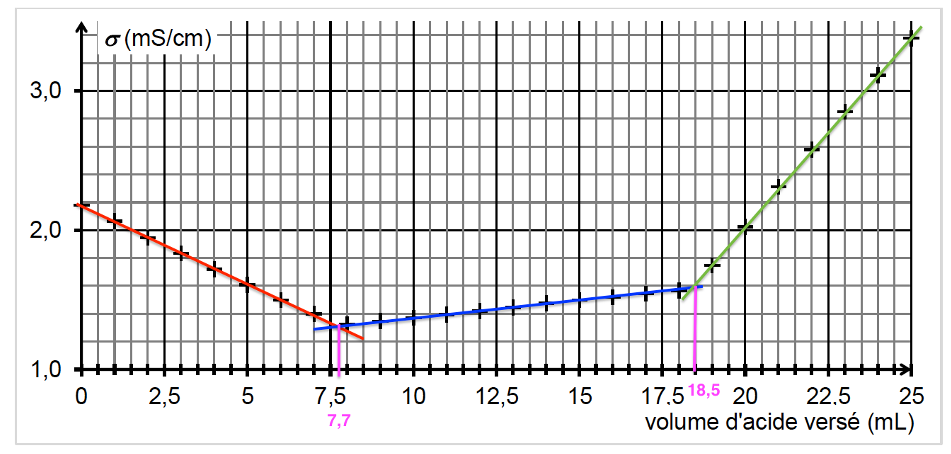
$$V_{eqvanillate}=V_{eq2}-V_{eq1}$$

$$V_{eqvanillate}=18,5-7,7$$

$$V_{eqvanillate}=10,8\ \text{mL}$$

2.6. En déduire la valeur de la concentration C_V^– en ions vanillinate dans la solution S₁.

À l’équivalence :

$$\frac{n_{V^-}^i}{1}=\frac{n_{H_3O^+}^{eq}}{1}$$

$$C_{V^-}\times V_1=C_a\times V_{eqvanillate}$$

$$C_{V^-}=\frac{C_a\times V_{eqvanillate}}{V_1}$$

$$C_{V^-}=\frac{1,0\times 10^{-1}\times 10,8\times 10^{-3}}{20,0\times 10^{-3}}$$

$$C_{V^-}=5,4\times 10^{-2}\ \text{mol·L}^{-1}$$

3. Dosage de la vanilline dans l’arôme alimentaire de vanille Bourbon

Protocole utilisé

• Placer 1,0 mL d’arôme alimentaire de vanille Bourbon dans une ampoule à décanter avec un peu d’eau.
• Extraire la vanilline présente dans la phase aqueuse à l’aide d’éthanoate d’éthyle et conserver la phase organique obtenue dans l’ampoule à décanter.
• Extraire la vanilline présente dans la phase organique précédente avec une solution aqueuse d’hydroxyde de sodium.
• Transvaser la phase aqueuse obtenue dans une fiole jaugée de 250,0 mL et compléter au trait de jauge avec la solution d’hydroxyde de sodium. On appelle S₂ cette solution.

On réalise alors les spectres d’absorption UV-visible :

• de la solution S₂ obtenue à l’aide du protocole ci-dessus ;
• d’une solution S₃  obtenue en diluant 1000 fois la solution de référence S₁ étudiée dans la deuxième partie.

La concentration en vanilline dans la solution S3 est C_val = 5,3×10^-5 mol·L^–1.

On obtient les spectres ci-dessous.

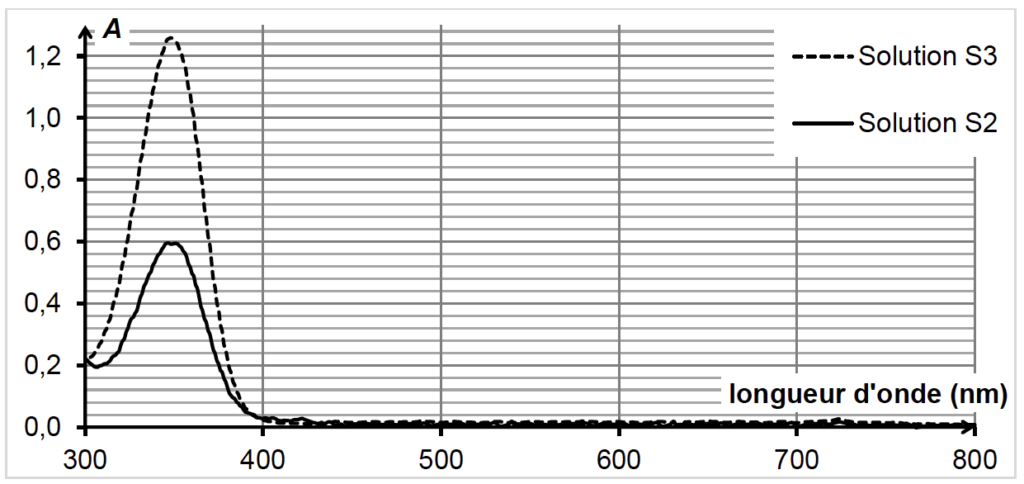
3.1. Les solutions S₂ et S₃ sont-elles colorées ? Justifier.

Les solutions S₂ et S₃ n’absorbent pas dans le visible : elles sont incolores.

3.2. Estimer la masse de vanilline présente dans 1 litre d’arôme alimentaire, en supposant la loi de Beer-Lambert vérifiée par les solutions dans les conditions de l’expérience.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Supposons que la loi de Beer-Lambert soit vérifiée par les solutions dans les conditions de l’expérience :

$$A=K\times C$$

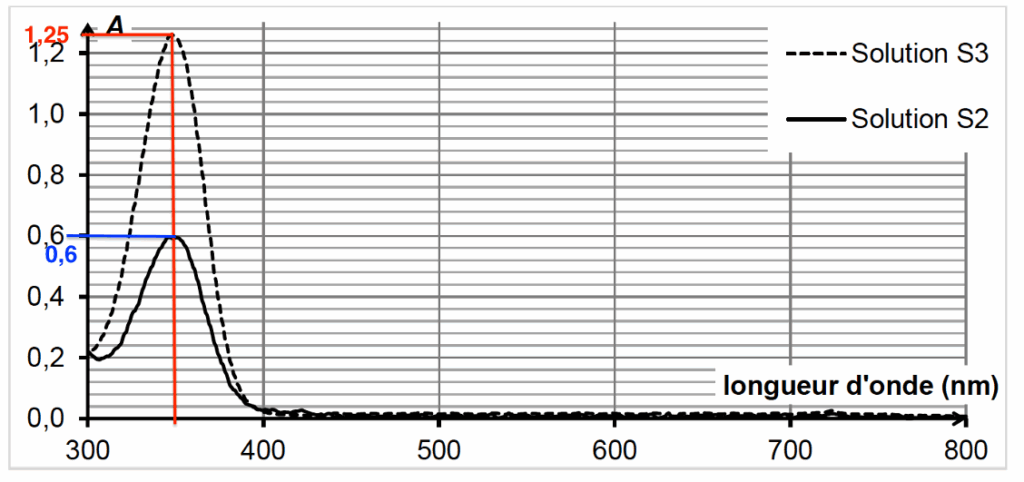
La concentration en vanilline dans la solution $S_3$ est $C_{\text{val}}=5,3\times 10^{-5}\ \text{mol·L}^{-1}$ et $A_3=1,25$.

$$A=K\times C$$

$$K=\frac{A}{C}$$

$$K=\frac{1,25}{5,3\times 10^{-5}}$$

$$K=2,4\times 10^{4}$$

D’où :

$$A=2,4\times 10^{4},C$$

Déterminons $C_2$ :

$$A_2=2,4\times 10^{4},C_2$$

$$C_2=\frac{A_2}{2,4\times 10^{4}}$$

$$C_2=\frac{0,60}{2,4\times 10^{4}}$$

$$C_2=2,5\times 10^{-5}\ \text{mol·L}^{-1}$$

Estimons la masse de vanilline présente dans 1 litre d’arôme alimentaire :

$$n=\frac{m}{M}$$

$$m=n\times M$$

Or

$$C=\frac{n}{V} \Rightarrow n=C\times V$$

Donc :

$$m=C\times V\times M$$

$$m=2,5\times 10^{-5}\times250\times 10^{-3}\times152$$

$$m=9,5\times 10^{-4}\ \text{g}$$

$m=9,5\times 10^{-4}\ \text{g}$ dans $1,0\ \text{mL}$ d’arôme alimentaire de vanille Bourbon.

$9,5\times 10^{-4}\ \text{g}$	1,0 mL
x	1,0 L

$$x=\frac{1,0\times9,5\times 10^{-4}}{1,0\times 10^{-3}}$$

$$x=0,95\ \text{g}$$

La masse de vanilline présente dans 1 litre d’arôme alimentaire est $0,95\ \text{g}$.