Polynésie 2025 Sujet 1
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°25-PYCJ1PO1
Sujet et corrigé
EXERCICE 1 – AUTOUR DE LA GLACE (9 POINTS)
L’objectif de cet exercice est de dater des couches de glace en Arctique par la méthode au plomb-210 puis de quantifier les ions argent présents dans les précipitations provoquées par ensemencement à l’iodure d’argent dans d’autres régions du monde.
1. Datation au plomb-210 d’une carotte de glace en Arctique.
La fonte progressive des glaciers met en péril l’approvisionnement en eau de nombreuses régions du globe et met à nu des couches de glace de plus en plus anciennes. Leur ancienneté peut être déterminée par radiodatation au plomb-210. C’est une méthode utilisée pour des échantillons dont l’âge estimé est inférieur à 150 ans. Dans l’atmosphère, le plomb-210 est issu de la désintégration du radon-222. Certaines méthodes de datation dites au plomb-210 utilisent le rayonnement α issu du polonium-210, dernier noyau radioactif de la chaîne de désintégrations.
Données :
- la désintégration β– s’accompagne de l’émission d’un électron $^{0}_{-1}e$.
- la désintégration α s’accompagne de l’émission d’un noyau d’hélium $^{4}_2He$.

Figure 1. Diagramme (Z,N), adapté du site ostralo.net.
Q1. À l’aide du diagramme (Z,N) de la figure 1, déterminer le type de désintégration que subit le plomb-210.
D’après le diagramme (Z,N) de la figure 1, le plomb-210 subit une désintégration β−.
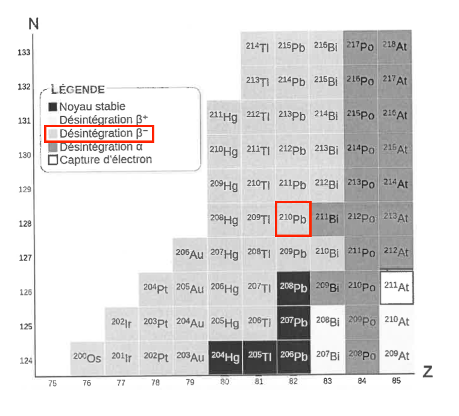
Q2. À l’aide de la figure 1 et des lois de conservation, établir l’équation modélisant la désintégration radioactive du plomb-210 amenant à la formation du bismuth-210.
Le plomb-210 subit une désintégration amenant à la formation du bismuth-210 :
$${_{82}^{210}}Pb\longrightarrow{_{83}^{210}}Bi+{_Z^A}X$$
Pour trouver A et Z on utilise les lois de Soddy :
Conservation du nombre de nucléons :
$$210=210+A$$
$$210+A=210$$
$$A=210-210$$
$$A=0$$
Conservation du nombre de charge :
$$82=83+Z$$
$$83+Z=82$$
$$Z=82-83$$
$$Z=-1$$
Ainsi ${_Z^A}X={_{-1}^0}e$
Le plomb-210 subit une désintégration amenant à la formation du bismuth-210 :
$${_{82}^{210}}Pb\longrightarrow{_{83}^{210}}Bi+{_{-1}^0}e$$
Il s’agit bien d’une désintégration β−.
Le bismuth-210 subit ensuite une désintégration β– pour former le polonium-210. Ce dernier, également instable, se désintègre à son tour.
Q3. À l’aide du diagramme (Z,N) de la figure 1, indiquer le noyau formé à l’issue de la désintégration du polonium-210. Justifier que le polonium-210 est le « dernier noyau radioactif » de la chaîne de désintégration du plomb-210.
D’après le diagramme (Z,N) de la figure 1, le polonium-210 subit une désintégration α.
$${_{84}^{210}}Po\longrightarrow{_Z^A}X+{_2^4}He$$
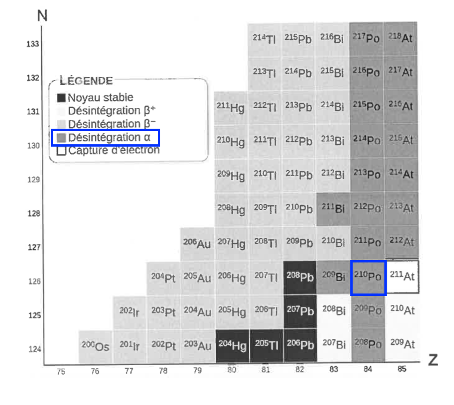
Conservation du nombre de nucléons :
$$210=A+4$$
$$A+4=210$$
$$A=210-4$$
$$A=206$$
Conservation du nombre de charge :
$$84=Z+2$$
$$Z+2=84$$
$$Z=84-2$$
$$Z=82$$
Ainsi ${_Z^A}X={_{82}^{206}}Pb$
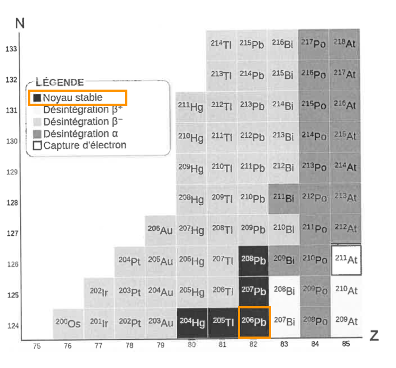
Le noyau issu de la désintégration α du polonium-210 est le plomb-206. D’après le diagramme (Z,N) de la figure 1, le plomb-206 est un élément stable.
Ainsi, le polonium-210 est le « dernier noyau radioactif » de la chaine de désintégration du plomb-210.
L’activité d’un échantillon de noyaux radioactifs est le nombre de désintégrations radioactives par unité de temps dans cet échantillon.
Q4. Donner la relation entre l’activité A(t) d’un échantillon et la dérivée temporelle du nombre de noyaux radioactifs N(t) dans l’échantillon.
$$A\left(t\right)=-\frac{dN\left(t\right)}{dt}$$
L’activité A(t) d’un échantillon radioactif est proportionnelle au nombre de noyaux radioactifs présents N(t). On écrit A(t) = λ×N(t) où la constante de proportionnalité λ est nommée constante radioactive et ne dépend que du type de noyaux radioactifs de l’échantillon.
Q5. Établir l’équation différentielle régissant la population de noyaux radioactifs N(t) sous la forme $\frac{dN(t)}{dt} + \lambda \cdot N(t)=0.$
$$A\left(t\right)=-\frac{dN\left(t\right)}{dt}$$
Or
$$A\left(t\right)=\lambda\times N\left(t\right)$$
D’où
$$\lambda\times N\left(t\right)=-\frac{dN\left(t\right)}{dt}$$
$$\frac{dN\left(t\right)}{dt}+\lambda\times N\left(t\right)=0$$
Q6. Vérifier que N(t) = N0∙e− λ∙t est solution de l’équation différentielle précédente, avec N0 le nombre de noyaux radioactifs initialement présents dans l’échantillon.
Solution de l’équation différentielle :
$$N\left(t\right)=N_0\times e^{-\lambda t}$$
Dérivons $N_{Rb}\left(t\right)$ :
$$\frac{dN\left(t\right)}{dt}=N_0\times-\lambda\times e^{-\lambda t}$$
$$\frac{dN\left(t\right)}{dt}=-\lambda\times N_0\times e^{-\lambda t}$$
$$\frac{dN\left(t\right)}{dt}=-\lambda\times N\left(t\right)$$
On retrouve l’équation différentielle :
$$\frac{dN\left(t\right)}{dt}+\lambda\times N\left(t\right)=0$$
Ainsi, $N\left(t\right)=N_0\times e^{-\lambda t}$ est solution de l’équation différentielle.
Données :
- demi-vies t1/2 de différents noyaux radioactifs :
| Noyau radioactif | Plomb-210 210Pb | Bismuth-210 210Bi | Polonium-210 210Po |
| Demi-vie t1/2 | 22,2 ans | 5,0 jours | 138 jours |
Q7. Démontrer que le temps de demi-vie $t_{1/2}$ est relié à la constante radioactive λ par : $t_{1/2}=\frac{\ln(2)}{\lambda}.$ Calculer la constante radioactive $\lambda_{Pb}$ du plomb-210.
$t_{1/2}$ est la durée au bout de laquelle le nombre de noyau radioactif (ou l’activité) a été divisée par 2.
$$N(t_{1/2})=\frac{N_0}{2}$$
Or
$$N(t_{1/2})=N_0\times e^{-\lambda t_{1/2}}$$
Ainsi
$$N_0\times e^{-\lambda t_{1/2}}=\frac{N_0}{2}$$
$$e^{-\lambda t_{1/2}}=\frac{1}{2}$$
$$ln\left(e^{-\lambda t_{1/2}}\right)=ln\left(\frac{1}{2}\right)$$
$$-\lambda t_{1/2}=-ln\left(2\right)$$
$$\lambda=\frac{ln\ 2}{t_{1/2}}$$
$$\lambda_{Pb}=\frac{\ln 2}{t_{1/2Pb}}$$
$$\lambda_{Pb}=\frac{\ln 2}{22,2}$$
$$\lambda_{Pb}=3,12 \times 10^{-2}\ \text{an}^{-1}$$
Dans la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
En 1993, des chercheurs de l’université de Yamagata au Japon ont daté les différentes couches d’une carotte de glace dans l’archipel norvégien de Svalbard à l’aide de cette méthode. À une profondeur de 30 m, une masse de 1 kg de glace avait une activité A30 = 4,72 mBq liée au plomb 210. On supposera que l’activité d’un kilogramme de glace liée au plomb-210 valait A0 = 110 mBq à sa formation.
Q8. Déterminer l’année à laquelle la glace présente à 30 m de profondeur s’est formée. En déduire l’épaisseur moyenne de glace accumulée chaque année sur l’archipel durant cette période.
$$A_{30}=A_0\times e^{-\lambda\times t_{30}}$$
$$A_0\times e^{-\lambda\times t_{30}}=A_{30}$$
$$e^{-\lambda\times t_{30}}=\frac{A_{30}}{A_0}$$
$$ln\left(e^{-\lambda\times t_{30}}\right)=ln\left(\frac{A_{30}}{A_0}\right)$$
$$-\lambda\times t_{30}=ln\left(\frac{A_{30}}{A_0}\right)$$
Or
$$\lambda=\frac{ln\ 2}{t_{1/2}}$$
$$-\frac{ln\ 2}{t_{1/2}}\times t_{30}=ln\left(\frac{A_{30}}{A_0}\right)$$
$$t_{30}=-ln\left(\frac{A_{30}}{A_0}\right)\times\frac{t_{1/2}}{ln\ 2}$$
$$t_{30}=-ln\left(\frac{4,72\times{10}^{-3}}{110\times{10}^{-3}}\right)\times\frac{22,2}{ln\ 2}$$
$$t_{30}=100\ ans$$
La glace présente à 30 m de profondeur s’est formée 100 ans avant son extraction.
Or elle a été extraite en 1993 :
1993-100=1893
Ainsi, la glace présente à 30 m de profondeur s’est formée en 1893.
Calculons l’épaisseur moyenne de glace accumulée chaque année sur l’archipel durant cette période.
| 30 m | 100 ans |
| e | 1 an |
$$e=\frac{1\times30}{100}$$
$$e=0,30\ m$$ Ainsi, l’épaisseur moyenne de glace accumulée chaque année sur l’archipel durant cette période est de 0,30 m.
2. Contrôle de la grêle par ensemencement à l’iodure d’argent.
Les tempêtes de grêle peuvent causer des dommages d’autant plus importants que les grêlons sont gros. En pulvérisant de l’iodure d’argent dans les nuages, on cherche à favoriser la formation d’un nombre plus important de grêlons mais de taille moindre.
L’ensemencement des nuages est une méthode de contrôle météorologique appliquée pour la première fois en 1946. Elle est utilisée partout dans le monde, avec comme objectif la dispersion du brouillard ou encore la lutte contre la désertification.
Cette technologie apporte des ions argent Ag+ dans l’environnement, qu’il importe de quantifier. Le département de chimie de l’université de Al-Qadisiyah en Irak a développé une méthode spectrophotométrique permettant de déterminer la quantité d’ions argent présents dans un échantillon. Elle repose sur la réaction des ions Ag+(aq) avec la molécule 6-(4BrPAA) appelée « ligand », selon la réaction chimique modélisée par l’équation suivante :
Ag+ (aq) + ligand (aq) ⇄ Ag(ligand)+ (aq) (1)
La structure de la molécule constituant le ligand est représentée figure 2 :

Figure 2. Structure du ligand.
Q9. Nommer le type de représentation utilisé pour la molécule de ligand représentée sur la figure 2.
La représentation utilisée pour la molécule de ligand représentée sur la figure 2 est une représentation topologique.
Q10. Nommer les deux familles fonctionnelles correspondant aux groupes caractéristiques A et B entourés sur la figure 2.
Famille fonctionnelle du groupe caractéristique A : Halogène (bromo)
Famille fonctionnelle du groupe caractéristique B : amine
Donnée :
- on définit la concentration standard c° = 1 mol∙L–1.
Q11. Écrire la constante d’équilibre de la réaction de formation de Ag(ligand)+ (aq) en fonction des concentrations à l’équilibre des différentes espèces et de la concentration standard co.
$${\rm Ag}^+\left(aq\right)+ligand\left(aq\right)\longrightarrow{Ag(ligand)}^+\left(aq\right)$$
$$Q_{eq}=K=\frac{\frac{\left[{Ag(ligand)}^+\right]{eq}}{c^0}}{\frac{\left[{\rm Ag}^+\right]{eq}}{c^0}\times\frac{\left[ligand\right]{eq}}{c^0}}$$
$$K=\frac{\frac{\left[{Ag(ligand)}^+\right]{eq}}{c^0}}{\frac{\left[{\rm Ag}^+\right]{eq}\times\left[ligand\right]{eq}}{\left(c^0\right)^2}}$$
$$K=\frac{\left[{Ag(ligand)}^+\right]{eq}}{c^0}\times\frac{\left(c^0\right)^2}{\left[{\rm Ag}^+\right]{eq}\times\left[ligand\right]{eq}}$$
$$K=\left[{Ag(ligand)}^+\right]{eq}\times\frac{c^0}{\left[{\rm Ag}^+\right]{eq}\times\left[ligand\right]{eq}}$$
$$K=\frac{\left[{Ag(ligand)}^+\right]{eq}\times c^0}{\left[{\rm Ag}^+\right]{eq}\times\left[ligand\right]_{eq}}$$
Q12. Justifier que la réaction de formation de Ag(ligand)+ (aq) est quasi-totale si le ligand est en très fort excès.
Qr est inversement proportionnel à la concentration en ligand.
Si le ligand est en très fort excès Qr sera très petit, la réaction se produira dans le sens direct et la réaction sera quasi-totale.
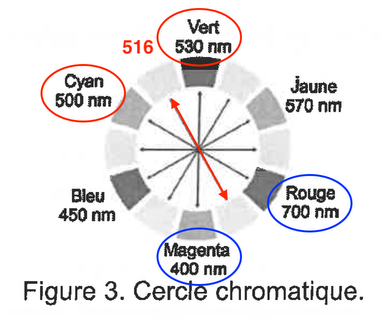
Les solutions aqueuses contenant l’espèce chimique Ag(ligand)+ (aq) sont colorées, ce qui permet d’utiliser une méthode de dosage spectrophotométrique en étudiant l’absorbance de la solution. L’espèce chimique Ag(ligand)+ (aq) possède un pic d’absorbance pour une longueur d’onde λmax = 516 nm. On donne le cercle chromatique sur la figure 3.
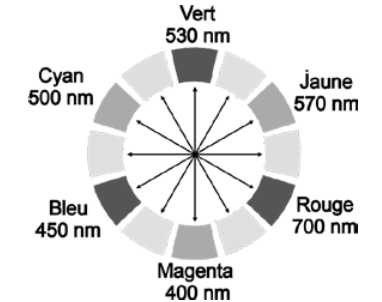
Figure 3. Cercle chromatique.
Q13. En vous aidant de la figure 3, déterminer la couleur des solutions aqueuses contenant l’espèce chimique Ag(ligand)+ (aq).
La couleur absorbée correspond à $\lambda_{max}=516\ nm$ couleur cyan-vert absorbée.
Sa couleur est la couleur complémentaire du cyan-vert (couleur opposée sur la cercle chromatique) : le magenta-rouge.
Ainsi, l’espèce Ag(ligand)+(aq) est de couleur magenta-rouge.
On mélange un volume VAg+ = 1,0 mL d’une solution de concentration d’ion argent [Ag+] = 7,4×10–6 mol∙L–1 avec un volume VL de solution de ligand à la concentration cL = 1,0×10–3 mol∙L–1.
Q14. Calculer la quantité de matière en ions argent nAg,i initialement introduite dans la solution.
$$\left[{\rm Ag}^+\right]=\frac{n_{{\rm Ag}^+,i}}{V_{{\rm Ag}^+}}$$
$$\frac{n_{{\rm Ag}^+,i}}{V_{{\rm Ag}^+}}=\left[{\rm Ag}^+\right]$$
$$n_{{\rm Ag}^+,i}=\left[{\rm Ag}^+\right]\times V_{{\rm Ag}^+}$$
$$n_{{\rm Ag}^+,i}=7,4\times{10}^{-6}\times 1,0\times{10}^{-3}$$
$$n_{{\rm Ag}^+,i}=7,4\times{10}^{-9}\ mol$$
On mesure l’absorbance des différentes solutions obtenues, à la longueur d’onde λmax = 516 nm. Les résultats obtenus sont reportés dans la figure 4.
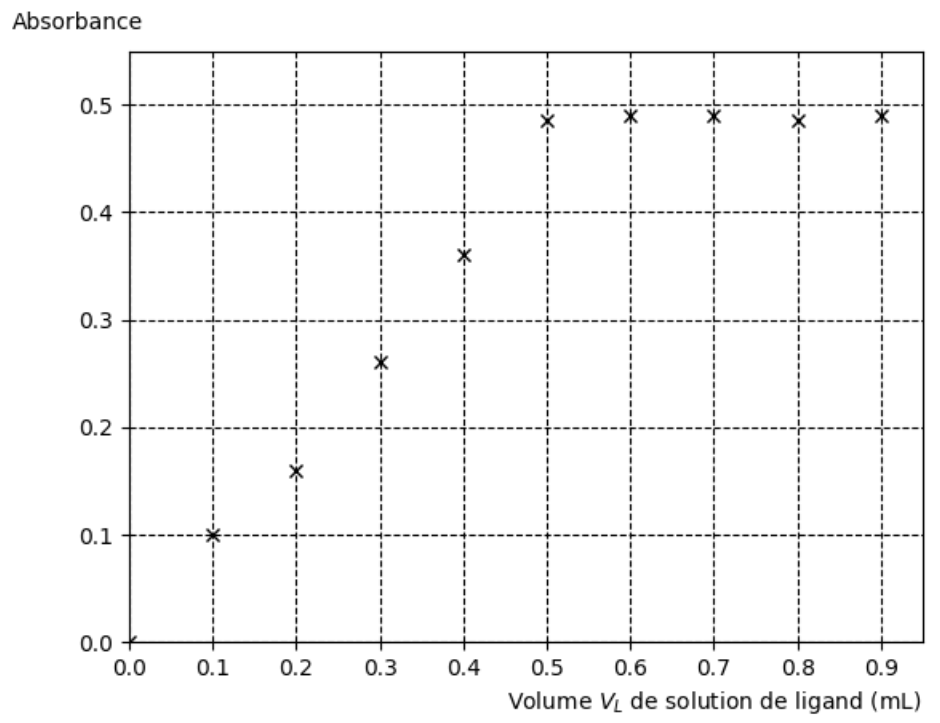
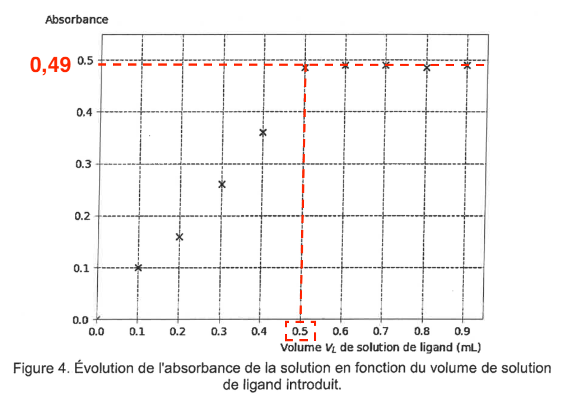
Figure 4. Évolution de l’absorbance de la solution en fonction du volume de solution de ligand introduit.
On constate qu’à partir d’un certain volume introduit, la quantité de Ag(ligand)+ (aq) n’évolue plus, ce qui signifie que pratiquement tous les ions argent Ag+ (aq) ont réagi avec le ligand.
Q15. À l’aide de la figure 4, déterminer le volume Vtot,L de solution de ligand versé pour que l’ensemble des ions argent Ag+ (aq) présents aient réagi en quasi-totalité. Calculer la quantité de matière de ligand nL à introduire.
Les ions argent Ag+ (aq) réagissent et forment les ions Ag(ligand) + (aq).
Les ions Ag(ligand)+ (aq) absorbent à $\lambda_{max}=516\ nm$.
L’absorbance est proportionnelle à la concentration des ions Ag(ligand)+ (aq).
Lorsque l’ensemble des ions argent Ag+ (aq) ont réagi, la quantité d’ion Ag(ligand)+ (aq) n’évolue plus et l’absorbance également.
L’absorbance n’évolue plus pour $V_{tot,L}=0,50\ mL$.
Graphiquement, le volume $V_{tot,L}$ de solution de ligand versé pour que l’ensemble des ions argent Ag+ (aq) présents aient réagi en quasi-totalité est $V_{tot,L}=0,50\ mL$.
Calculons la quantité de matière de ligand $n_L$ à introduire :
$$c_L=\frac{n_L}{V_{tot,L}}$$
$$\frac{n_L}{V_{tot,L}}=c_L$$
$$n_L=c_L\times V_{tot,L}$$
$$n_L=1,0\times{10}^{-3}\times0,5\times{10}^{-3}$$
$$n_L=5,0\times{10}^{-7}\ mol$$
Q16. Vérifier que le ligand est bien en large excès par rapport aux ions Ag+ (aq) initialement introduits. Commenter ce résultat.
$${\rm Ag}^+\left(aq\right)+ligand\left(aq\right)\longrightarrow{Ag(ligand)}^+\left(aq\right)$$
Méthode 1 (sans tableau d’avancement) :
$$x_{max\ 1}=\frac{n_{{\rm Ag}^+,i}}{1}$$
$$x_{max\ 1}=\frac{7,4\times{10}^{-9}}{1}$$
$$x_{max\ 1}=7,4\times{10}^{-9}\ mol$$
$$x_{max\ 2}=\frac{n_L}{1}$$
$$x_{max\ 2}=\frac{5,0\times{10}^{-7}}{1}$$
$$x_{max\ 2}=5,0\times{10}^{-7}\ mol$$
$$x_{max\ 1}\ll x_{max\ 2}$$
$$x_{max}=x_{max\ 1}=7,4\times{10}^{-9}\ mol$$
Ainsi, le ligand est bien en large excès par rapport aux ions Ag+ (aq) initialement introduits.
Méthode 2 (avec tableau d’avancement) :
| Équation | ${\rm Ag}^+\left(aq\right)$ | $)+ligand\left(aq\right)$ | $\longrightarrow{Ag(ligand)}^+\left(aq\right)$ |
| État initial | $7,4\times{10}^{-9}$ | $5,0\times{10}^{-7}$ | 0 |
| État intermédiaire | $7,4\times{10}^{-9}-x$ | $5,0\times{10}^{-7}-x$ | x |
| État final | $7,4\times{10}^{-9}-x_f$ | $5,0\times{10}^{-7}-x_f$ | xf |
$$7,4\times{10}^{-9}-x_{max\ 1}=0$$
$$-x_{max\ 1}=7,4\times{10}^{-9}$$
$$x_{max\ 1}=7,4\times{10}^{-9}\ mol$$
$$5,0\times{10}^{-7}-x_{max\ 2}=0$$
$$-x_{max\ 2}=-5,0\times{10}^{-7}$$
$$x_{max\ 2}=5,0\times{10}^{-7}\ mol$$
$$x_{max\ 1}\ll x_{max\ 2}$$
$$x_{max}=x_{max\ 1}=7,4\times{10}^{-9}\ mol$$
Ainsi, le ligand est bien en large excès par rapport aux ions Ag+ (aq) initialement introduits.
D’après la question Q12 : si le ligand est en très fort excès la réaction sera quasi-totale. Cette condition est remplie, la réaction sera quasi-totale.
Q17. En supposant la réaction totale et en utilisant la loi de Beer-Lambert, montrer que l’absorbance de la solution de l’espèce chimique Ag(ligand)+ (aq) est proportionnelle à la concentration en quantité de matière en ions argent initialement en solution cAg,i. On pourra éventuellement s’aider d’un tableau d’avancement.
| Équation | ${\rm Ag}^+\left(aq\right)$ | $+ligand\left(aq\right)$ | $\longrightarrow{Ag(ligand)}^+\left(aq\right)$ |
| État initial | $c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}$ | Excès | 0 |
| État intermédiaire | $c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}-x$ | Excès | x |
| État final en considérant la réaction totale $x_f=x_{max}$ | $c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}-x_{max}=0$ | Excès | $x_{max}$ |
Loi de Beer-Lambert :
$$A=K\times\left[{Ag(ligand)}^+\right]$$
Or
$$\left[{Ag(ligand)}^+\right]=\frac{n_{{Ag(ligand)}^+}}{V_{sol}}$$
$$A=K\times\frac{n_{{Ag(ligand)}^+}}{V_{sol}}$$
Or
$$n_{{Ag(ligand)}^+}=x_{max}$$
D’ou
$$A=K\times\frac{x_{max}}{V_{sol}}$$
Or
$$c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}-x_{max}=0$$
$$-x_{max}=-c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}$$
$$x_{max}=c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}$$
D’ou
$$A=K\times\frac{c_{{\rm Ag}^+,i}\times V_{{\rm Ag}^+}}{V_{sol}}$$
Ainsi, l’absorbance de la solution de l’espèce chimique Ag(ligand)+ (aq) est proportionnelle à la concentration en quantité de matière en ions argent initialement en solution CAg,i.
Les chercheurs de l’université de Al-Qadisiyah ont indiqué que pour des concentrations en masse d’ions argent comprises entre cm,min = 9×10−3 µg·mL–1 et cm,max = 1,5 µg·mL–1, l’absorbance A de la solution de l’espèce chimique Ag(ligand)+ (aq) est reliée à la concentration en quantité de matière c (en mol·L–1) en ions argent par : A = 6,5×104×c.
Donnée :
- masse molaire atomique de l’argent : M(Ag) = 108 g·mol–1;
- valeur limite de mesure du spectrophotomètre à λ = 516 nm : Amax=0,9.
Q18. Vérifier que la valeur maximale de la concentration en masse en ions argent, cm,max , indiquée par les chercheurs est cohérente avec une limite expérimentale de la loi de Beer-Lambert.
$$A=6,5\times{10}^4\times c$$
$$A_{max}=6,5\times{10}^4\times c_{max}$$
$$6,5\times{10}^4\times c_{max}=A_{max}$$
$$c_{max}=\frac{A_{max}}{6,5\times{10}^4}$$
$$c_{max}=\frac{0,9}{6,5\times{10}^4}$$
$$c_{max}=1,4\times{10}^{-5}\ mol.L^{-1}$$
$$c_{m,max}=c_{m,max}\times M$$
$$c_{m,max}=1,4\times{10}^{-5}\times108$$
$$c_{m,max}=1,5\times{10}^{-3}\ g.L^{-1}$$
$$c_{m,max}=1,5\times{10}^{-3}\times{10}^{-3}\ g.{\rm mL}^{-1}$$
$$c_{m,max}=1,5\times{10}^{-6}\ g.{\rm mL}^{-1}$$
$$c_{m,max}=1,5\ \mu g.{\rm mL}^{-1}$$
Ainsi, la valeur maximale de la concentration en masse en ions argent, $c_{m,max}=1,5\ \mu g.{\rm mL}^{-1}$ , indiquée par les chercheurs est cohérente avec une limite expérimentale de la loi de Beer Lambert $c_{m,max}=1,5\ \mu g.{\rm mL}^{-1}$.
