Asie 2025 Sujet 2
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°25-PYCJ2JA1
Sujet et corrigé
Exercice 1 – Batteries au lithium (9 points)
Le 9 octobre 2019, le prix Nobel de chimie a récompensé trois scientifiques pour leurs recherches sur les batteries lithium-ion. Ces batteries rechargeables avec une capacité de stockage d’énergie inédite alimentent aujourd’hui de nombreux appareils électroniques et voitures électriques.
Dans cet exercice, on s’intéresse d’abord à une méthode d’extraction du lithium puis au fonctionnement d’un type de batterie lithium-ion.
Partie 1 – Extraction du lithium
Le lithium peut être extrait de solutions aqueuses concentrées appelées saumures. La dissolution de carbonate de sodium Na2CO3(s) dans une saumure entraîne la formation d’un précipité de carbonate de lithium LiCO3(s) récupéré par filtration.
On considère que 90 % du lithium initialement présent dans la saumure est récupéré si la concentration en masse en ions carbonate présents dans le filtrat est au minimum égale à Cm0 = 60,0 g·L-1.
Données :
- Couples acido-basiques et pKA associés :
- H2CO3(aq) / HCO– (aq) pKA1 = 6,3
- HCO3– (aq) / CO32-(aq) pKA2 = 10,3
Masse molaire des ions carbonate : M (CO32-(aq)) = 60,0 g·mol−1
Après avoir fait réagir une saumure avec du carbonate de sodium et filtré le mélange, un industriel souhaite savoir si l’objectif de récupérer 90 % du lithium présent dans la saumure est atteint.
Un volume V = 200,0 mL d’une solution S est préparé en diluant au centième le filtrat obtenu. Un volume V1 = 5,0 mL de la solution S est titré par pH-métrie avec une solution d’acide chlorhydrique (H3O+(aq) + C𝓁−(aq)) de concentration c2 = 1,00 × 10–2 mol·L–1.
Q1- Donner la liste de la verrerie à utiliser pour préparer la solution S par dilution du filtrat.
D’après l’énoncé : « Un volume V = 200,0 mL d’une solution S est préparé en diluant au centième le filtrat obtenu »
$$F=\frac{V}{V_0}$$
$$F\times V_0=V$$
$$V_0=\frac{V}{F}$$
$$V_0=\frac{200,0}{100}$$
$$V_0=2,0\ mL$$
On choisit :
une fiole jaugée V=200,0 mL
une pipette jaugée V0=2,0 mL
Q2- Tracer le diagramme de prédominance des espèces acido-basiques H2CO3(aq), HCO3– (aq), CO32-(aq)
Diagramme de prédominance :

Q3- Indiquer l’espèce prédominante présente initialement dans la solution titrée sachant que son pH initial est égal à 11,4.
Diagramme de prédominance :

Pour pH initial est égal à 11,4 : CO32- est prédominant
Q4- Préciser, en justifiant, si cette espèce est un acide, une base ou un ampholyte.
${\rm CO}_{3(aq)}^{2-}$ est capable de capter un proton H+ : c’est une base.
L’équation de la réaction support du titrage est :
CO32-(aq) + 2 H3O+(aq) → H2CO3(aq) + 2 H2O (𝓁)
Le volume de la solution titrante versé à l’équivalence de ce titrage est VE = 15,2 mL.
Q5- Définir l’équivalence d’un titrage.
L’équivalence d’un titrage est atteinte lorsque les réactifs sont introduits dans les proportions stœchiométriques.
Q6- Donner la relation entre la quantité de matière initiale des ions carbonate n0 (CO32–) et la quantité de matière des ions oxonium nE(H3O+) versée à l’équivalence.
$${\rm CO}3^{2-}(aq)+2H_3O^+(aq)\rightarrow H_2CO_3(aq)+2H_2O(l)$$
A l’équivalence :
$$\frac{n^{i}{{\rm CO}_3^{2-}}}{1}=\frac{n^{eq}{H_3O^+}}{2}$$
$$n_0({\rm CO}_3^{2-})=\frac{n_e(H_3O^+)}{2}$$
Q7- Déterminer si l’objectif d’extraction du lithium de la saumure est atteint.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
$$n_0({\rm CO}_3^{2-})=\frac{n_e(H_3O^+)}{2}$$
$$c{\text{dilué}}\times V_1=c_2\times V_{E2}$$
$$c_{\text{dilué}}=\frac{c_2\times V_{E2}}{V_1}$$
$$c_{\text{dilué}}=\frac{1,00\times 10^{-2}\times 15,2\times 10^{-3}}{2\times 5,0\times 10^{-3}}$$
$$c_{\text{dilué}}=1,52\times 10^{-2}\ mol.L^{-1}$$
D’après le sujet : « la solution S est préparé en diluant au centième le filtrat obtenu »
$$c=100\times c_{\text{dilué}}$$
$$c=100\times 1,52\times 10^{-2}$$
$$c=1,52\ mol.L^{-1}$$
D’après le sujet : « On considère que 90% du lithium initialement présent dans la saumure est récupéré si la concentration en masse en ions carbonate présents dans le filtrat est au minimum égale à Cmo = 60,0 g.L-1. »
Calculons la concentration massique en ions carbonate :
$$c_m=c\times M$$
$$c_m=1,52\times 60,0$$
$$c_m=91,2\ g.L^{-1}$$
La concentration en masse en ions carbonate présents dans le filtrat est supérieure à Cmo = 60,0 g.L-1 : l’objectif d’extraction du lithium de la saumure est atteint
Partie 2 – Fonctionnement d’une batterie lithium-ion
Document – Description d’une batterie lithium-ion
Une batterie est composée de plusieurs piles individuelles connectées les unes aux autres.
La figure 1 ci-dessous schématise une de ces piles.
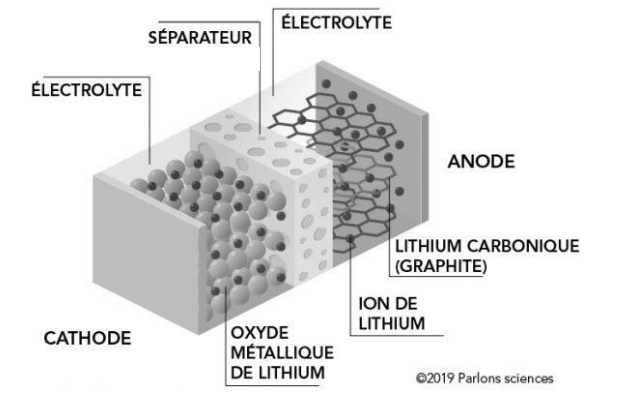
Figure 1 : Schéma d’une pile lithium-ion
Lors du fonctionnement de la pile, une réaction a lieu à chaque électrode :
Réaction 1 : l’oxyde de cobalt (CoO2(s)) se combine aux ions lithium (Li+(aq)) pour
former l’oxyde métallique de lithium (LiCoO2 (s)) :
CoO2(s) + Li+(aq) + e- = LiCoO2(s)
Réaction 2 : le composé lithium carbonique, de formule LiC6(s), forme des ions
lithium ( Li+(aq)) et du graphite (C6(s)) :
LiC6(s) = Li+(aq)(aq) + C6(s) + e–
D’après le site https://parlonssciences.ca/
Données :
- Charge élémentaire : e = 1,60 × 10−19 C
- Constante d’Avogadro : NA = 6,02 × 1023 mol−1
- Équivalence ampère-heure / coulomb : 1,0 A·h = 3,6 × 103 C
- Masse molaire : M (LiC6) = 79,0 g·mol−1
- Relation entre charge électrique Q (en C) et quantité de matière (en mol) d’électrons n(e-) :
Q = n(e–) x NA x e
Q8- Associer, en justifiant, les réactions 1 et 2 aux électrodes cathode et anode mentionnées sur la figure 1.
${\rm CoO}_2(s)+{\rm Li}^+(aq)+e^-=2\ Li{\rm CoO}_2(s)$ : gain d’électrons, c’est une réduction. Cette réaction (1) se déroule à la cathode.
${\rm LiC}_6(s)\rightarrow {\rm Li}^+(aq)+C_6(s)+e^-$ : perte d’électrons, c’est une oxydation. Cette réaction (2) se déroule à l’anode.
On donne sur l’ANNEXE p. 9 A RENDRE AVEC LA COPIE un schéma simplifié de la pile lors de sa décharge dans un récepteur.
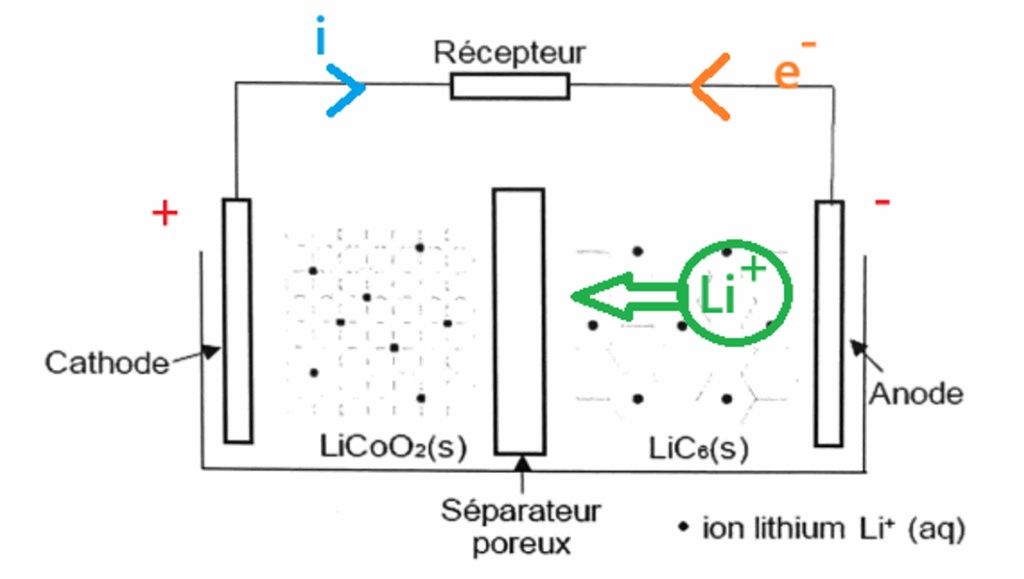
Q9- Faire apparaître sur le schéma de l’ANNEXE p. 9 A RENDRE AVEC LA COPIE :
- les polarités de pile ;
- le sens du courant électrique à l’extérieur de la pile ;
- le nom et le sens de déplacement des porteurs de charge à l’extérieur de pile ;
- le mouvement des ions lithium au sein de la pile.
${\rm LiC}_6(s)\rightarrow {\rm Li}^+(aq)+C_6(s)+e^-$ se déroule à l’anode. Cette réaction libère des électrons : c’est la borne négative de la pile.
${\rm CoO}_2(s)+{\rm Li}^+(aq)+e^-=2\ Li{\rm CoO}_2(s)$ se déroule à la cathode. Cette réaction consomme des électrons : c’est la borne positive de la pile.
Le sens du courant électrique à l’extérieur de la pile va de la borne positive vers la borne négative.
À l’extérieur de la pile les porteurs de charge sont les électrons qui se déplacent de la borne négative vers la borne positive.
Les ions lithium sont créés à l’anode et sont consommés à la cathode : les ions lithium se déplacent de l’anode vers la cathode.
Une batterie lithium-ion, d’une capacité totale Q = 214 A·h, équipe un véhicule électrique présentant une autonomie de 500 km.
Q10- Calculer la valeur de la quantité de matière d’électrons n(e-) échangés lors d’une décharge complète de la batterie.
$$Q=n(e^-)\times N_A\times e$$
$$n(e^-)=\frac{Q}{N_A\times e}$$
$$n(e^-)=\frac{214\times 3,6\times 10^3}{6,02\times 10^{23}\times 1,60\times 10^{-19}}$$
$$n(e^-)=8,00\ mol$$
Q11- En déduire la valeur de la masse m(LiC6) de LiC6(s) nécessaire.
D’après la demi-équation : ${\rm LiC}_6(s)\rightarrow {\rm Li}^+(aq)+C_6(s)+e^-$
$$\frac{n({\rm LiC}_6)}{1}=\frac{n(e^-)}{1}$$
$$n({\rm LiC}_6)=n(e^-)$$
Or
$$n({\rm LiC}_6)=\frac{m({\rm LiC}_6)}{M({\rm LiC}_6)}$$
D’où
$$\frac{m({\rm LiC}_6)}{M({\rm LiC}_6)}=n(e^-)$$
$$m({\rm LiC}_6)=n(e^-)\times M({\rm LiC}_6)$$
$$m({\rm LiC}_6)=8,00\times 79,0$$
$$m({\rm LiC}_6)=632\ g$$
Ainsi, la masse m(LiC6) de LiC6(s) nécessaire est de 632g.
ANNEXE A RENDRE AVEC LA COPIE
Exercice 1 – Schéma simplifié d’une pile lithium – ion