Bac Amérique du Sud 2022 Sujet 2
Exercice B – (5 points) – Au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n°22-PYCJ2AS1
Sujet et corrigé
EXERCICE B. BESOINS EN MAGNÉSIUM
Mots-clés : titrage avec suivi colorimétrique, exploitation de mesures
Le magnésium est un oligoélément indispensable à notre organisme. Il intervient dans le bon fonctionnement des systèmes musculaires et nerveux, la santé osseuse et la synthèse des protéines et de l’ADN. L’organisme humain ne peut pas produire ses propres réserves de magnésium aussi faut-il lui en apporter par le biais de l’alimentation.
En France, pour un adulte, l’Agence Nationale de Sécurité Sanitaire de l’Alimentation, de l’Environnement et du Travail (ANSES) a conseillé un apport en magnésium de 6 mg/jour/kg.
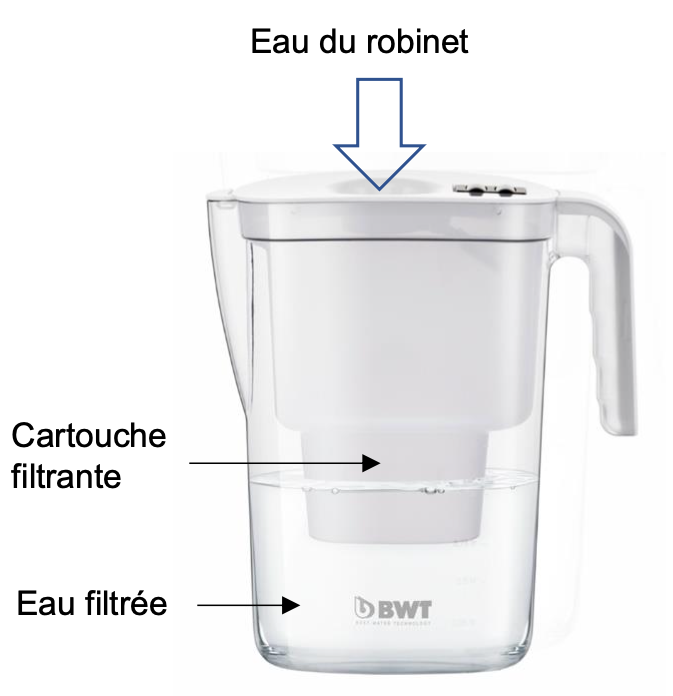
Les cartouches « Edition Mg2+ » disponibles pour des carafes filtrantes permettraient de faire consommer une eau enrichie en magnésium.
Dans une cartouche filtrante « Edition Mg2+ », l’eau passe notamment par une résine échangeuse d’ions qui va éliminer le tartre et les métaux lourds ; les ions calcium présents dans l’eau sont alors remplacés par des ions magnésium […]
D’après https://www.bwt.com/fr-fr/
Le but de cet exercice est de vérifier l’efficacité de ces cartouches filtrantes relative au remplacement des ions calcium par des ions magnésium.
Données
- Masses molaires : M(Mg) = 24,3 g·mol-1 M(Ca) = 40,1 g·mol-1
- Méthode de détermination de la concentration totale en ions magnésium et calcium.
La concentration totale en ions magnésium et en ions calcium d’une eau peut être déterminée grâce à un titrage par l’EDTA (acide éthylènediaminetétraacétique) en présence d’un indicateur coloré de fin de réaction et d’une solution tampon permettant de maintenir le 𝑝𝐻 de la solution entre 9 et 10.
La concentration de la solution d’EDTA utilisée est 𝑐 = 1,0 × 10−2 mol⋅L−1.
En milieu basique, l’EDTA contient des ions Y4− (ions éthylènediaminetétraacétate) qui réagissent avec les ions magnésium (Mg2+) et avec les ions calcium (Ca2+). Ces transformations chimiques sont modélisables par deux réactions représentées par les équations suivantes :
Mg2+(aq) + Y4−(aq) → MgY2−(aq)
Ca2+(aq) + Y4−(aq) → CaY2−(aq)
- Méthode de détermination de la concentration en ions calcium
La concentration en ions calcium d’une eau est déterminée grâce à un titrage par l’EDTA, à un 𝑝𝐻 supérieur à 12, en présence d’un indicateur coloré de fin de réaction. Dans ce domaine de 𝑝𝐻, les ions magnésium forment un précipité.
La concentration de la solution d’EDTA utilisée est 𝑐 = 1,0 × 10−2 mol⋅L−1. La réaction, support du titrage, modélisant la transformation s’écrit :
Ca2+(aq) + Y4−(aq) → CaY2−(aq)
Sur de l’eau obtenue après filtration avec une carafe munie de la cartouche « édition Mg2+ », on réalise les deux titrages décrits pour déterminer les concentrations des ions magnésium et calcium d’une part et les ions calcium seuls d’autre part.
Les deux titrages sont réalisés sur un volume 𝑉 = 100,0 mL d’eau filtrée. Les résultats obtenus sont les suivants :
| Volumes d’EDTA versés | Eau filtrée |
| Volume 𝑉𝐸 (en mL) d’EDTA versé pour atteindre l’équivalence lors du titrage des ions calcium | 8,8 |
| Volume 𝑉𝐸 (en mL) d’EDTA versé pour atteindre l’équivalence lors du titrage des ions magnésium et des ions calcium | 10,8 |
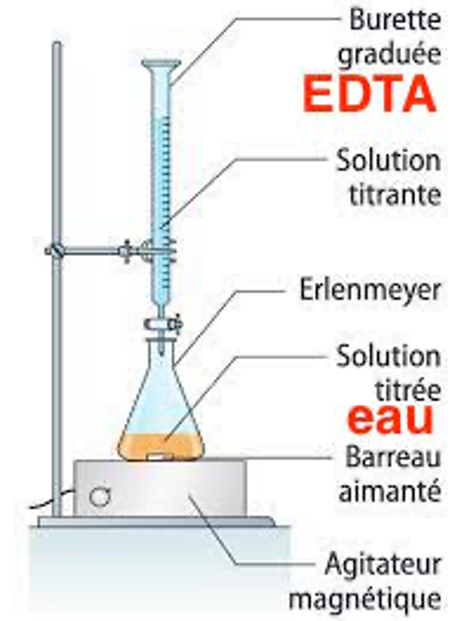
1. Réaliser le schéma légendé du montage permettant de réaliser le titrage des ions calcium présents dans une eau.
2. Pourquoi le titrage des ions calcium seuls est-il réalisé à un 𝑝𝐻 supérieur à 12 ?
Pour pH>12, les ions magnésium forment un précipité. Ainsi seul les ions calcium réagissent.
3. Déterminer la concentration en quantité de matière en ions calcium de l’eau filtrée.
${\rm Ca}^{2+}\left(aq\right)+Y^{4-}(aq)\rightarrow CaY^{2-}(aq)$
A l’équivalence, les réactifs ont été introduits dans les proportions stœchiométrique :
$\frac{n_{{\rm Ca}^{2+}}^i}{1}=\frac{n_{Y^{4-}}^{eq}}{1}$
$\left[{\rm Ca}^{2+}\right]\times V=c\times V_e$
$\left[{\rm Ca}^{2+}\right]=\frac{c\times V_e}{V}$
$\left[{\rm Ca}^{2+}\right]=\frac{1,0{.10}^{-2}\times 8,8{.10}^{-3}}{100,0{.10}^{-3}}$
$\left[{\rm Ca}^{2+}\right]=8,8{.10}^{-4}mol.L^{-1}$
$\left[{\rm Ca}^{2+}\right]=0,88\ mmol.L^{-1}$
4. Montrer que la concentration en quantité de matière en ions magnésium est égale à 0,20 mmol·L−1.
${\rm Mg}^{2+}\left(aq\right)+Y^{4-}(aq)\rightarrow MgY^{2-}(aq)$
A l’équivalence, les réactifs ont été introduits dans les proportions stœchiométrique :
$\frac{n_{{\rm Mg}^{2+}}^i}{1}=\frac{n_{Y^{4-}}^{eq}}{1}$
$\left[{\rm Mg}^{2+}\right]\times V=c\times V_e$
$\left[{\rm Mg}^{2+}\right]=\frac{c\times V_e}{V}$
Attention $V_e$ est le volume à l’équivalence pour le titrage des ions magnésium exclusivement soit :
$V_e=10,8-8,8=2,0\ mL$
$\left[{\rm Mg}^{2+}\right]=\frac{1,0{.10}^{-2}\times 2,0{.10}^{-3}}{100,0{.10}^{-3}}$
$\left[{\rm Mg}^{2+}\right]=2,0{.10}^{-4}mol.L^{-1}$
$\left[{\rm Mg}^{2+}\right]=0,20\ mmol.L^{-1}$
Un technicien de laboratoire procède à l’analyse de l’eau du robinet non filtrée et fournit les résultats suivants :
| Concentrations en quantité de matière | Eau non filtrée |
| Concentration en quantité de matière des ions calcium | 2,2 mmol·L−1 |
| Concentration en quantité de matière des ions calcium et magnésium | 2,3 mmol·L−1 |
5. Les résultats obtenus sont-ils en accord avec les propriétés annoncées pour la carafe filtrante munie de la cartouche « Edition Mg2+ » ?
La concentration en ions calcium pour une eau non filtrée est 2,2 mmol.L-1
La concentration en ions calcium et magnésium pour une eau non filtrée est 2,3 mmol.L-1
La concentration en magnésium pour une eau non filtrée est donc 2,3-2,2=0,1 mmol.L-1
L’eau filtrée à une concentration en ion magnésium de 0,2 mmol.L-1
« Dans une cartouche filtrante « Edition Mg2+ », l’eau passe notamment par une résine échangeuse d’ions qui va éliminer le tartre et les métaux lourds ; les ions calcium présents dans l’eau sont alors remplacés par des ions magnésium […] »
Seulement une petite quantité d’ion calcium a été remplacée par des ions magnésium.
Les résultats obtenus montre une efficacité limitée de la cartouche « Edition Mg2+».
6. Un adulte de masse 70 kg peut-il couvrir ses besoins journaliers en magnésium en consommant uniquement de l’eau filtrée ?
En France, pour un adulte, l’Agence Nationale de Sécurité Sanitaire de l’Alimentation, de l’Environnement et du Travail (ANSES) a conseillé un apport en magnésium de 6 mg/jour/kg.
Un adulte de 70 Kg doit donc absorber une masse de $m=70\times 6=420\ mg$
Calculons le volume nécessaire pour couvrir les besoins journaliers en magnésium en consommant uniquement de l’eau filtrée :
$c=\frac{n}{V}$
$V=\frac{n}{c}$
Or
$n=\frac{m}{M}$
D’ou
$V=\frac{\frac{m}{M}}{c}$
$V=\frac{m}{M\times c}$
$V=\frac{420\times {10}^{-3}}{24,3\times 0,2\times {10}^{-3}}$
$V=86\ L$
Ce volume est impossible à boire en une journée.
Un adulte de masse 70 kg ne peut pas couvrir ses besoins journaliers en magnésium en consommant uniquement de l’eau filtrée.
