Centrale électrique de l’Ouest Guyanais (CEOG)

E3C2 – 10 points – Durée 1h – calculatrice autorisée

En Guyane, le fonds Meridiam et HDF Energy vont financer et construire la plus grande centrale électrique non polluante au monde

HDF Energy s’inscrit comme le premier producteur mondial d’électricité́ stable à partir d’énergies intermittentes, en associant un parc photovoltaïque de puissance 55 MW avec le plus gros stockage de ressource d’énergie renouvelable au monde à base d’hydrogène. Cette combinaison permet ainsi de produire, dans la durée, une électricité́ stable avec une énergie 100 % propre.

La centrale électrique de L’Ouest Guyanais (CEOG) sera raccordée au réseau EDF, elle produira quotidiennement, sur une durée de 20 ans, une puissance électrique fixe de 10 MW la journée jusqu’au soir, et de 3,0 MW la nuit. La production électrique étant stable et garantie, le service rendu par CEOG sera équivalent aux centrales fonctionnant au diesel ou au gaz, mais sans pollution, ni logistique d’approvisionnement en carburant ou combustible. Le prix de l’électricité de CEOG sera inférieur à l’actuel coût de production dans l’Ouest guyanais, et ce, sans subvention.

La mise en service de CEOG est prévue à l’automne 2020.

Sources : d’après communiqué de presse HDF Energy et https://la1ere.francetvinfo.fr/guyane-fonds-meridiam-hdf-energy-vont-financer-construire-plus-grande-centrale-electrique-non-polluante-au-monde-626880.html

Le projet consiste à associer une centrale photovoltaïque à une centrale à dihydrogène.

L’énergie électrique non consommée produite par la centrale photovoltaïque en journée, est utilisée pour réaliser l’électrolyse de l’eau pour produire du dihydrogène. Ce dihydrogène est alors stocké sur place pour pouvoir être utilisé la nuit dans une pile à combustible.

La première partie de l’exercice est consacrée à la production et au stockage du dihydrogène. La deuxième partie est consacrée au fonctionnement électrique d’un électrolyseur.

Partie 1. Production et stockage du dihydrogène

On cherche dans un premier temps à dimensionner les différents réservoirs à utiliser pour stocker le dihydrogène produit par la centrale à dihydrogène.

Données :

masses molaires atomiques : M_H = 1,00 g.mol^-1; M_O = 16,0 g.mol^-1;
masse volumique de l’eau : ρ_eau = 1000 kg.m^– 3;
volume molaire : le volume molaire du dihydrogène gazeux à température ambiante de 25 °C et à la pression de 1,0×10⁵Pa est de V_m = 24 L.mol^-1.

Les couples d’oxydo-réduction mis en jeu pour l’obtention de dihydrogène lors de l’électrolyse de l’eau sont les suivants :

O_{2 (g)} / H₂O_(l)
H⁺_(aq)/ H₂ _(g)

1.1. Définir un oxydant et un réducteur.

Un oxydant est une espèce chimique capable de capter un ou plusieurs électrons.

Un réducteur est une espèce chimique capable de céder un ou plusieurs électrons.

1.2.1. Écrire les demi-équations électroniques associées aux deux couples mis en jeu.

O_{2 (g)} / H₂O_(l) : O_{2 (g)} +4H⁺+2e^– = H₂O_(l)

H⁺_(aq)/ H₂ _(g) : 2H⁺_(aq)+ 2e^– = H₂ _(g)

1.2.2. L’électrolyse de l’eau est modélisée par la réaction d’équation :

2 H₂O_(l) → 2 H_2(g) + O_2(g)

L’électrolyseur devra permettre de produire une masse de 50 kg de dihydrogène en journée.

Déterminer la valeur de la quantité de matière de dihydrogène à produire n(H₂) en journée.

$n_{H_2}= \frac{m_{H_2}}{M_{H_2}}$

$n_{H_2}= \frac{50.10^{3}}{2 \times 1,00}=2,5.10^{4} mol$

1.2.3. Calculer la masse d’eau m(H₂O) nécessaire pour produire les 50 kg de dihydrogène à stocker durant la journée.

$m_{H_2O}= m_{H_2O}^{consommé} \times m_{H_2O}$

équation de réaction : 2 H₂O_(l) → 2 H_2(g) + O_2(g)

$\frac{n_{H_2}^{produite}}{2}= \frac{{n_{H_2O}^{consommé}}}{2}$

${n_{H_2}^{produite}}= n_{H_2O}^{consommé}$

D’ou

$m_{H_2O}= {n_{H_2}^{produite}} \times m_{H_2O}$

$m_{H_2O}= 2,5.10^{4} \times (2 \times 1,00+16,0)$

$m_{H_2O}= 4,5.10^{5} g= 450 Kg$

1.2.4. Déterminer le volume minimum du réservoir d’eau V(H₂O).

$\rho_{H_2O}= \frac{m_{H_2O}}{V_{H_2O}}$

$V_{H_2O}= \frac{m_{H_2O}}{\rho_{H_2O}}$

$V_{H_2O}= \frac{450}{1000}=0,45 m^3 = 450 L$

1.3.1. Le stockage du dihydrogène s’effectue quant à lui généralement avec des bouteilles ou assemblages de bouteilles cylindriques, en acier, portées à une pression P_stock de 5,0×10⁶ Pa. En utilisant la loi de Mariotte, déterminer le volume nécessaire V_stock des bouteilles pour stocker le dihydrogène.

Loi de Mariotte : Pour une quantité de gaz constante, à une température constante le produit de la pression p et du volume V est constant.

P.V=Constante

$P_{stock}\times V_{stock}=P_{atm}\times V_{atm}$

$V_{stock}=\frac {P_{atm}\times V_{atm}} {P_{stock}}$

$n_{H_2}= \frac{V_{atm}}{V_{m}}$

$V_{atm}=n_{H_2} \times {V_{m}$

D’ou

$V_{stock}=\frac {P_{atm}\times n_{H_2}\times V_{m}}{P_{stock}}$

$V_{stock}=\frac {{1,0.10^5 \times 2,5.10^4 \times 24}} {5,0.10^6}=1,2.10^4 L$

1.3.2. Commenter les résultats sachant que le parc photovoltaïque s’étend sur une surface de 700 000 m².

$V_{stock}=1,2.10^4 L=12 m^3$

C’est un volume faible au vu de la surface de stockage disponible.

Partie 2. Étude du fonctionnement électrique d’un électrolyseur

On cherche maintenant à caractériser le fonctionnement électrique d’un électrolyseur pouvant servir à produire du dihydrogène.

L’électrolyse de l’eau est réalisée au laboratoire à l’aide du montage électrique suivant :

En faisant varier la tension U aux bornes de l’électrolyseur, on mesure pour chaque valeur de la tension U, l’intensité du courant I dans le circuit de l’électrolyseur. On obtient le tableau de résultats suivant :

U (en V)	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0	10,0	11,0	12,0
I (en mA)	0,0	0,0	0,0	0,1	3,4	9,7	16,2	21,9	27,9	34,8	40,5	47,2	53,5

La caractéristique représentant l’évolution de la tension U aux bornes de l’électrolyseur en fonction de l’intensité du courant I, est représentée ci-après.

Une partie de la courbe obtenue est modélisable par l’équation U = E’ + r’.I où :

E’ est la force contre-électromotrice de l’électrolyseur exprimée en volt (V) ;
r’ est la résistance interne de l’électrolyseur exprimée en ohm (W).

Caractéristique U en fonction de I :

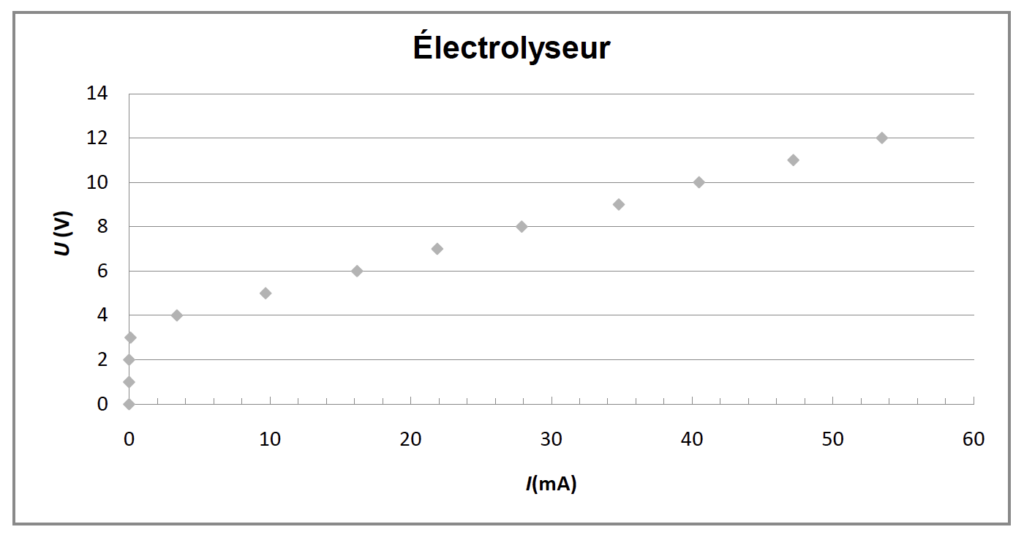
Équation de la droite déterminée à l’aide d’un logiciel de calcul : U = 3,46 + 160 × I où U exprimée en V et I en A.

2.1. Sans recopier la chaîne énergétique ci-dessous, donner la forme d’énergie à faire apparaître dans chaque cadre numéroté de 1 à 3.

Pour cela, indiquer sur la copie le numéro du cadre et lui associer une expression choisie parmi les suivantes : énergie chimique ; énergie électrique ; énergie lumineuse ; énergie mécanique ; énergie thermique.

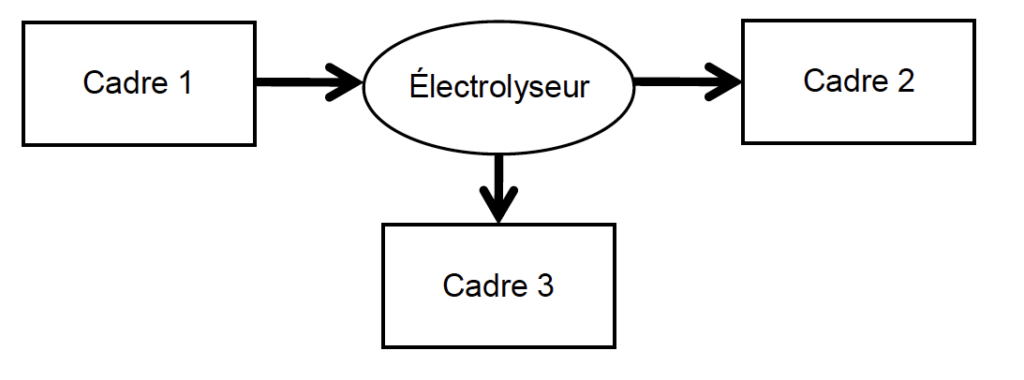
Cadre 1 : énergie électrique

Cadre 2 : énergie chimique

Cadre 3 : énergie thermique

2.2. Déterminer, en utilisant la modélisation effectuée par le logiciel de calcul, les valeurs des grandeurs physiques E’ et r’ pour cet électrolyseur.

La courbe obtenue est modélisable par l’équation : U = E’ + r’.I

La droite déterminée à l’aide d’un logiciel de calcul : U = 3,46 + 160 × I

Par identification :

E’=3,46 V

r’=160 Ω

2.3.1. Donner l’expression littérale de l’énergie totale reçue E_reçue par l’électrolyseur s’il fonctionne pendant une durée Dt en fonction de U, I et Δt.

$E_{recue}= P \times \Delta t}$

$P= U \times I}$

$E_{recue}= U \times I \times \Delta t}$

2.3.2. Donner l’expression littérale de l’énergie totale dissipée E_dissipée par l’électrolyseur sous forme d’effet Joule s’il fonctionne pendant une durée Δt.

L’énergie totale dissipée E_dissipée par l’électrolyseur sous forme d’effet Joule est due à la résistance interne

$E_{dissipée}= P_{J} \times \Delta t}$

$E_{dissipée}= U_{r'} \times I \times \Delta t}$

$U_{r'}= r' \times I }$

$E_{dissipée}= r' \times I \times I \times \Delta t}$

$E_{dissipée}= r' \times I^2 \times \Delta t}$

2.3.3. En déduire que l’expression littérale du rendement de l’électrolyseur est

$\eta = \frac{E'}{U}$

$\eta = \frac{E_{utile}}{E_{recue}}$

Avec :

$E_{recue}= U \times I \times \Delta t}$

$E_{utile}= E_{recue}-E_{dissipée}}$

D’ou

$\eta = \frac{U \times I \times \Delta t - r' \times I^2 \times \Delta t}{U \times I \times \Delta t}$

$\eta = \frac{ I \times \Delta t (U- r' \times I)}{U \times I \times \Delta t}$

$\eta = \frac{(U- r' \times I)}{U}$

Or U = E’ + r’.I

E’ = U- r’.I

D’ou

$\eta = \frac{E'}{U}$

2.3.4. Calculer le rendement de cet électrolyseur pour un courant d’intensité I = 50 mA.

$\eta = \frac{E'}{U}$

$\eta = \frac{E'}{E'-r'\times I}$

$\eta = \frac{3,46}{3,46+160 \times 50.10^{-3}}$

$\eta = 0,302=30,2\%$

2.4. En s’appuyant sur les données de l’énoncé et les réponses aux questions précédentes, expliquer en quoi le projet semble être une bonne alternative aux énergies fossiles.

« Cette combinaison permet ainsi de produire, dans la durée, une électricité stable avec une énergie 100 % propre. », il n y a pas de production de gaz a effet de serre.

« La production électrique étant stable et garantie », nous pouvons compter sur un approvisionnement sur et stable de cette centrale contrairement à des centrales dont la production est intermittente.

De plus, la place pour le stockage de l’hydrogène est faible.

C’est pourquoi, le projet semble être une bonne alternative aux énergies fossiles.