Coloration capillaire

Bac Polynésie 2024 Sujet 1

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°24-PYCJ1PO1

EXERCICE 1 – COLORATION CAPILLAIRE (9 POINTS)

Changer la couleur des cheveux, pigmenter de nouveau un cheveu blanchi par l’âge, voilà la promesse des colorations capillaires. Différentes techniques sont envisageables : les colorations naturelles, qui enrobent la fibre de pigments provenant du monde végétal, et les colorations d’origine synthétique. Parmi elles, les colorations d’oxydation promettent une longue tenue, car les espèces colorantes sont enfermées dans la fibre capillaire.

Le mélange colorant est préparé juste avant l’application, le coiffeur mélange la plupart du temps des volumes sensiblement égaux de solution oxydante à base de peroxyde d’hydrogène et de crème colorante contenant les précurseurs de la molécule colorée et les coupleurs. Cette crème contient également de l’ammoniaque ou une amine organique pour garantir un milieu basique. Après un temps de pose pour développer la couleur et un rinçage, un shampoing neutralise l’effet de l’ammoniaque.

L’objectif de cet exercice est d’étudier quelques aspects de la formule des produits professionnels permettant de teindre les cheveux de manière durable.

Étude de solutions oxydantes.

Les solutions oxydantes utilisées pour développer les colorations capillaires contiennent du peroxyde d’hydrogène H₂O₂(aq). Le tableau de la figure 1 présente différentes solutions oxydantes disponibles à l’usage des professionnels de la coiffure, leur pourcentage en masse de peroxyde d’hydrogène et leur masse volumique.

Solutions oxydantes	Pourcentage en masse de peroxyde d’hydrogène dans la solution	Masse volumique de la solution (en g·L–1)
Solution n°1	3,0 %	1011
Solution n°2	6,0 %	1022
Solution n°3	9,0 %	1033
Solution n°4	12,0 %	1044

Figure 1. Tableau des différents oxydants disponibles avec leur pourcentage en masse de peroxyde d’hydrogène et leur masse volumique.

Il est possible de déterminer la concentration en quantité de matière en peroxyde d’hydrogène H₂O₂ d’une solution oxydante pour coloration capillaire à l’aide d’un dosage par titrage. Le réactif titrant est le permanganate de potassium (K⁺(aq) ; MnO₄^–(aq)) en milieu acide.

L’équation de la réaction modélisant la transformation observée durant le dosage par titrage est :

$$2\ {\rm MnO_4^-}(aq)+6\ {\rm H^+}(aq)+5\ {\rm H_2O_2}(aq)\ \rightarrow\ 2\ {\rm Mn^{2+}}(aq)+5\ {\rm O_2}(g)+8\ {\rm H_2O}(\ell)$$

La solution oxydante, notée S, est préalablement diluée au vingtième ainsi sa concentration en quantité de matière est divisée par 20. La solution obtenue est notée S₂₀.

Q1. Donner le protocole, en indiquant la verrerie, qui permet de préparer un volume V de valeur égale à 100 mL de solution S₂₀ à partir de la solution S.

$F=\frac{V}{V_0}$
$F\times V_0=V$
$V_0=\frac{V}{F}$
$V_0=\frac{100}{20}$
$V_0=5,0\ mL$

Protocole de la dilution :

• Prendre une fiole jaugée de volume V=100 mL.
• Ajouter à l’aide d’une pipette jaugée le volume V₀=5,0 mL de la solution mère à prélever dans la fiole jaugée.
• Ajouter au ¾ de l’eau distillée. Agiter.
• Ajuster avec de l’eau distillée jusqu’au trait de jauge.
• Homogénéiser

On place un volume V₁ de solution S₂₀ dans un erlenmeyer et on ajoute quelques gouttes d’une solution d’acide sulfurique concentrée. La burette contient la solution de permanganate de potassium (K⁺(aq) ; MnO₄^–(aq)) de concentration en quantité de matière c₂. Le volume de solution de permanganate de potassium pour atteindre l’équivalence est noté V_E.

Données :

• Valeur du volume V₁ : V₁ = 10,0 mL ;
• Valeur de la concentration en quantité de matière c₂ de la solution de permanganate de potassium (K⁺(aq) ; MnO₄^–(aq)) : c₂ = 2,00×10^–2 mol·L^–1 ;
• Valeur du volume V_E  de solution de permanganate de potassium versé à l’équivalence : V_E = 18,1 mL ;
• Valeur de la masse molaire du peroxyde d’hydrogène : M_H2O2 = 34 g·mol^–1.

Q2. Établir la relation à l’équivalence entre la quantité de matière du peroxyde d’hydrogène n₁ et la quantité de matière n_2E des ions permanganate.

$2{{\rm MnO}_4^-}{(aq)}+6{H^+}{(aq)}+5H_2O_{2(aq)}\rightarrow2{{\rm Mn}^{2+}}{(aq)}+5O_{2(aq)}+8H_2O_{(l)}$
A l’équivalence, les réactifs ont été introduits dans les proportions stœchiométrique :
$\frac{n_{H_2O_2}^i}{5}=\frac{n_{{\rm MnO}4^-}^{eq}}{2}$
$\frac{n_1}{5}=\frac{n{2E}}{2}$

Q3. Déterminer c₁, la concentration en quantité de matière du peroxyde d’hydrogène de la solution S₂₀.

$\frac{n_1}{5}=\frac{n_{2E}}{2}$
$\frac{c_1\times V_1}{5}=\frac{c_2\times V_E}{2}$
$c_1=\frac{5\times c_2\times V_E}{2\times V_1}$
$c_1=\frac{5\times 2,00\times {10}^{-2}\times 18,1}{2\times 10,0}$
$c_1=9,05\times {10}^{-2}\ mol.L^{-1}$

Q4. En déduire la concentration en quantité de matière c du peroxyde d’hydrogène dans la solution oxydante S.

$F=\frac{c}{c_1}$
$\frac{c}{c_1}=F$
$c=F\times c_1$
$c=20\times 9,05\times {10}^{-2}$
$c=1,81\ mol.L^{-1}$

Q5. Vérifier, à l’aide des valeurs du tableau de la figure 1, que la solution oxydante étudiée est la solution n°2.

Calculons la concentration en peroxyde d’hydrogène de la solution 2 :
$c=\frac{n_{H_2O_2}}{V_{Solution}}$
Or
$n_{H_2O_2}=\frac{m_{H_2O_2}}{M_{H_2O_2}}$

Ainsi :
$c=\frac{n_{H_2O_2}}{V_{Solution}}=\frac{m_{H_2O_2}}{M_{H_2O_2}\times V_{Solution}}$

Or le pourcentage est défini par :
$w=\frac{m_{H_2O_2}}{m_{solution}}$

D’ou
$m_{H_2O_2}=w\times m_{solution}$

Ainsi :
$c=\frac{m_{H_2O_2}}{M_{H_2O_2}\times V_{Solution}}=\frac{w\times m_{solution}}{M_{H_2O_2}\times V_{Solution}}$

Or
$\rho_{solution}=\frac{m_{solution}}{V_{Solution}}$

Ainsi :
$c=\frac{w\times m_{solution}}{M_{H_2O_2}\times V_{Solution}}=\frac{w\times \rho_{solution}}{M_{H_2O_2}}$
$c=\frac{\frac{6,0}{100}\times 1022}{34}$
$c=1,8\ mol.L^{-1}$

La concentration calculée est la même que celle trouvée par le dosage Q5. Ainsi, a solution oxydante étudiée est la solution n°2.

Le titre en volume correspond au volume de dioxygène libéré par la décomposition en eau et en dioxygène d’un litre de solution de peroxyde d’hydrogène dans les conditions normales de température et de pression.

L’équation de la réaction modélisant la décomposition du peroxyde d’hydrogène est la suivante :

2 H₂O₂(aq) → O₂(g) + 2 H₂O(l)

Le tableau de la figure 2 présente des informations concernant la solution n°2, son pourcentage en masse de peroxyde d’hydrogène, son titre en volume et sa masse volumique.

Solution oxydante	Pourcentage en masse de peroxyde d’hydrogène dans la solution	Titre en volume (en volumes)	Masse volumique de la solution (en g·L–1)
Solution n°2	6,0 %	20 volumes	1022

Figure 2 : Informations concernant la solution n°2.

Données :

• Volume molaire des gaz à température et pression normales : Vm = 22,4 L·mol^–1 ;
• Valeur de la masse molaire du peroxyde d’hydrogène : M_H2O2 = 34 g·mol^–1.

Pour la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Q6. Vérifier que la solution oxydante n°2 à 6,0 % en masse de peroxyde d’hydrogène dans la solution correspond effectivement à un titre en volume de valeur proche de 20 volumes.

D’après l’énoncé : Le titre en volume correspond au volume de dioxygène libéré par la décomposition en eau et en dioxygène d’un litre de solution de peroxyde d’hydrogène dans les conditions normales de température et de pression.
L’équation de la réaction modélisant la décomposition du peroxyde d’hydrogène est la suivante :
$2\ H_2O_2(aq)\longrightarrow O_2(g)+2\ H_2O(l)$

	$2\ H_2O_2(aq)$	$\longrightarrow O_2(g)$	$+\ 2\ H_2O(l)$
État initial	$c\times V_{solution}$	0	0
État intermédiaire	$c\times V_{solution}-2x$	$x$	$2x$
État final	$c\times V_{solution}-2x_f$	$x_f$	$2x_f$

Exprimons $x_{max}$ :
$c\times V_{solution}-2x_{max}=0$
$-2x_{max}=-c\times V_{solution}$
$2x_{max}=c\times V_{solution}$
$x_{max}=\frac{c\times V_{solution}}{2}$

La réaction étant totale (flèche dans l’équation de réaction) :
$x_f=x_{max}$
$x_f=\frac{c\times V_{solution}}{2}$

Exprimons le volume de dioxygène libéré :
$n_{O_2}^f=\frac{V_{O_2}}{V_m}$
$\frac{V_{O_2}}{V_m}=n_{O_2}^f$
$V_{O_2}=n_{O_2}^f\times V_m$

Or
$n_{O_2}^f=x_f$

D’où
$V_{O_2}=x_f\times V_m$

Ainsi
$V_{O_2}=\frac{c\times V_{solution}}{2}\times V_m$
$V_{O_2}=\frac{1,8\ \times 1,0}{2}\times 22,4$
$V_{O_2}=20\ L$

Ainsi, la solution oxydante n°2 à $6,0\ %$ en masse de peroxyde d’hydrogène dans la solution correspond effectivement à un titre en volume de valeur proche de 20 volumes.

Étude de la crème colorante.

La crème colorante contient une espèce basique ammoniaque ou amine organique dont la fonction est de fixer le pH du mélange colorant vers une valeur de 9,5. À ce pH, les écailles du cheveu s’ouvrent pour laisser les précurseurs des espèces colorées pénétrer abondamment la fibre.

Données :

• Couple acide-base ion ammonium / ammoniac : NH₄⁺ (aq) / NH₃ (aq) ;
• Couples acide/base de l’eau : H₃O⁺(aq) / H₂O (l) et H₂O (l) / HO^–(aq).

Q7. Écrire l’équation de la réaction modélisant l’action de l’eau sur l’ammoniac NH₃(aq).

Réaction modélisant l’action de l’eau $H_2O(l)$ sur l’ammoniac $NH_3(aq)$.

Couples :
${\rm NH}_4^+(aq)/{\rm NH}_3(aq)$
$H_3O^+(aq)/H_2O(l)$
$H_2O(l)/{\rm HO}^-(aq)$

L’eau est une espèce amphotère, elle est l’acide d’un couple et la base d’un autre.

$NH_3(aq)$ est une base, il réagit avec l’eau $H_2O(l)$ qui se comporte comme un acide.

${\rm NH}_4^+(aq)/{\rm NH}_3(aq)$
$H_2O(l)/{\rm HO}^-(aq)$

$H_2O(l)+{\rm NH}_3(aq)\rightleftarrows {\rm HO}^-(aq)+{\rm NH}_4^+(aq)$

Soit une solution aqueuse de concentration en quantité de matière c_A d’ammoniac de valeur égale à 1,00×10^–2 mol·L^–1. La valeur du pH de cette solution est égale à 10,6.

Donnée :

• Valeur du produit ionique de l’eau Ke à 25°C : Ke = 1,0×10^–14.
• Concentration standard : c° = 1,0 mol·L^–1.

Q8. Montrer que l’ammoniac est une base faible dans l’eau.

Méthode 1 :
Pour une base forte : $pH=14+\log(c)$ avec $c$ la concentration de la base

Calculons $14+\log(c)$ et comparons avec le $pH$ :
$14+\log(c)=14+\log(1,00\times {10}^{-2})$
$14+\log(c)=12$

Or $pH=10,6$
Ainsi $14+\log(c)\neq pH$ : l’ammoniac est une base faible dans l’eau.

Méthode 2 :
Une base forte réagit totalement avec l’eau : la réaction est totale.
Une base faible ne réagit pas totalement avec l’eau : la réaction est limitée.

	$H_2O(l)$	${\rm NH}_3(aq)$	$\rightleftarrows {\rm HO}^-(aq)$	$+ {\rm NH}_4^+(aq)$
État initial	Excès	$c_AV$	0	0
État intermédiaire	Excès	$c_AV-x$	$x$	$x$
État final	Excès	$c_AV-x_f$	$x_f$	$x_f$

Exprimons $x_{max}$ :
$c_AV-x_{max}=0$
$-x_{max}=-c_AV$
$x_{max}=c_AV$

Exprimons $x_f$ :
$x_f={n({\rm HO}^-)}_f$
$x_f=\left[{\rm HO}^-\right]_f V$

Calculons le taux d’avancement :
$\tau=\frac{x_f}{x_{max}}$
$\tau=\frac{\left[{\rm HO}^-\right]_f V}{c_AV}$
$\tau=\frac{\left[{\rm HO}^-\right]_f}{c_A}$

Or
$K_e=\left[H_3O^+\right]_f\times \left[{\rm HO}^-\right]_f$
$\left[H_3O^+\right]_f\times \left[{\rm HO}^-\right]_f=K_e$
$\left[{\rm HO}^-\right]_f=\frac{K_e}{\left[H_3O^+\right]_f}$

D’où
$\tau=\frac{\frac{K_e}{\left[H_3O^+\right]_f}}{c_A}$
$\tau=\frac{K_e}{c_A\times \left[H_3O^+\right]_f}$

Or
$\left[H_3O^+\right]_f=c^0\times {10}^{-pH}$

D’où
$\tau=\frac{K_e}{c_A\times c^0\times {10}^{-pH}}$
$\tau=\frac{1,0\times {10}^{-14}}{1,00\times {10}^{-2}\times 1,0\times {10}^{-10,6}}$
$\tau=0,04$
$\tau=4\ %$

La réaction est limitée : l’ammoniac est une base faible dans l’eau.

La valeur du pH mesurée dans le « mélange prêt à l’application » est égale à 9,2.

Donnée :

• Valeur du pK_A du couple ion ammonium / ammoniac à 25°C : pK_A = 9,2.

Q9. Tracer le diagramme de prédominance du couple ion ammonium / ammoniac.

Diagramme de prédominance du couple ion ammonium / ammoniac :

Le document de la figure 3 présente des composés employés presque systématiquement dans les colorations pour cheveux. Ce sont des composés qui peuvent s’oxyder très facilement.

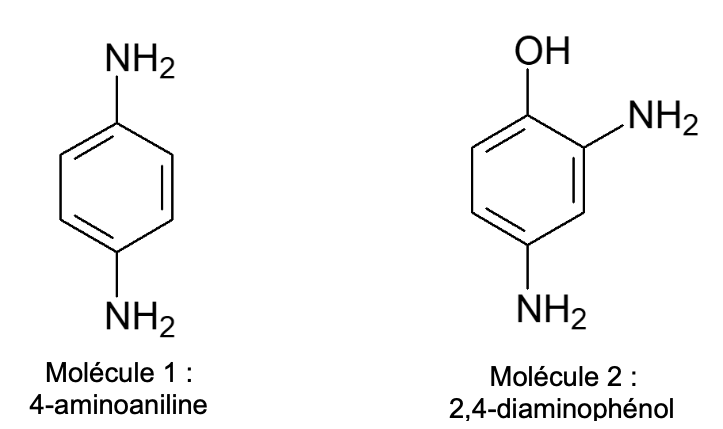
Figure 3 : Formules topologiques de composés employés dans les colorations pour cheveux.

Q10. Recopier la formule topologique de la molécule 2, entourer et nommer les groupes caractéristiques présents.

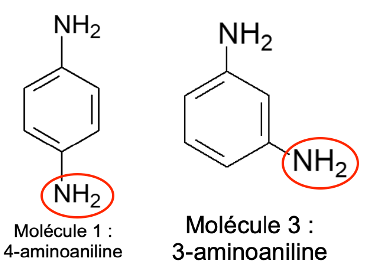
Les coupleurs sont un peu moins sensibles à l’oxydation que les molécules précédentes. Une relation structurelle, ou isomérie de constitution, entre les deux types de structure est responsable de cette différence. Le document de la figure 4 présente un coupleur le 3-aminoaniline.

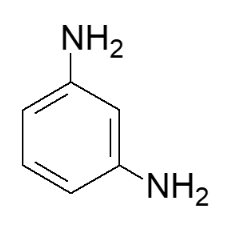
Molécule 3 : 3-aminoaniline

Figure 4. Formule topologique d’un coupleur.

Q11. Nommer la catégorie de l’isomérie de constitution entre la molécule 3 et la molécule 1.

Développement de la couleur.

Lorsque l’on mélange la crème colorante et la solution oxydante, une espèce colorée apparaît peu à peu. Cette espèce est capable de teindre le cheveu en s’insérant à l’intérieur de la fibre capillaire. Le développement de cette couleur peut être étudié au spectrophotomètre.

Lorsque la solution n’est pas trop concentrée, elle suit la loi de Beer-Lambert, qui peut permettre de vérifier la teneur en coupleur de la crème colorante.

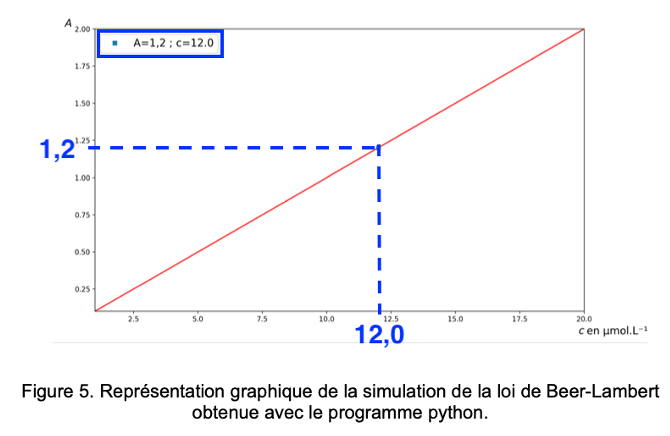
Pour réaliser une simulation de la loi de Beer-Lambert, on choisit d’utiliser un programme Python, qui lorsqu’il a été exécuté donne le résultat présenté figure 5.

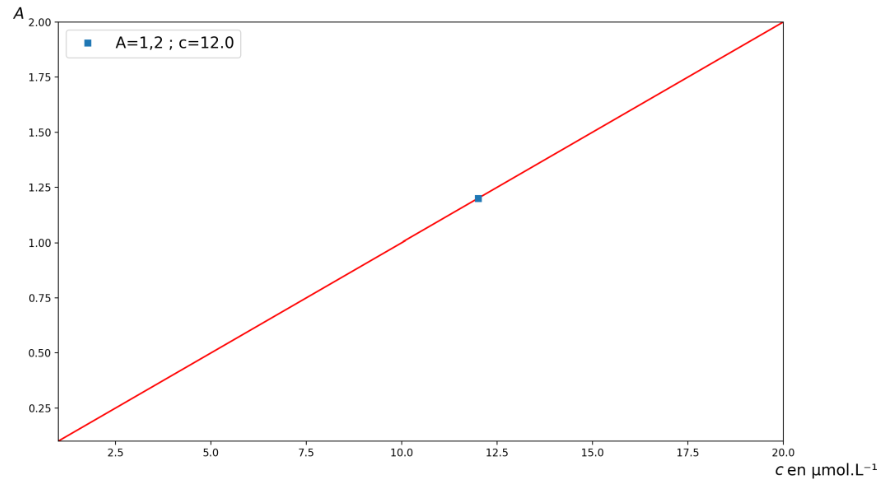
Figure 5. Représentation graphique de la simulation de la loi de Beer-Lambert obtenue avec le programme python.

Les solutions de la gamme d’étalonnage envisagée contiennent le colorant capillaire obtenu par oxydation de l’espèce qu’on appellera par la suite molécule C dans une gamme de concentration en quantité de matière comprise entre 1,0×10^–6 mol·L^–1 à 2,0×10^–5 mol·L^–1.

Données :

• La valeur de la longueur l de la cuve est égale à 1,0 cm ;
• La valeur du coefficient d’extinction molaire e (epsilon) de l’espèce colorée est égale à 1,00×10⁵ L·mol^–1·cm^–1 ;
• La loi de Beer-Lambert appliquée dans son domaine de validité s’écrit A= ε·l·c avec A la valeur de l’absorbance, e le coefficient d’extinction molaire de l’espèce, c la valeur de la concentration et l la valeur de la longueur de la cuve du spectrophotomètre.

Le programme Python est présenté figure 6.

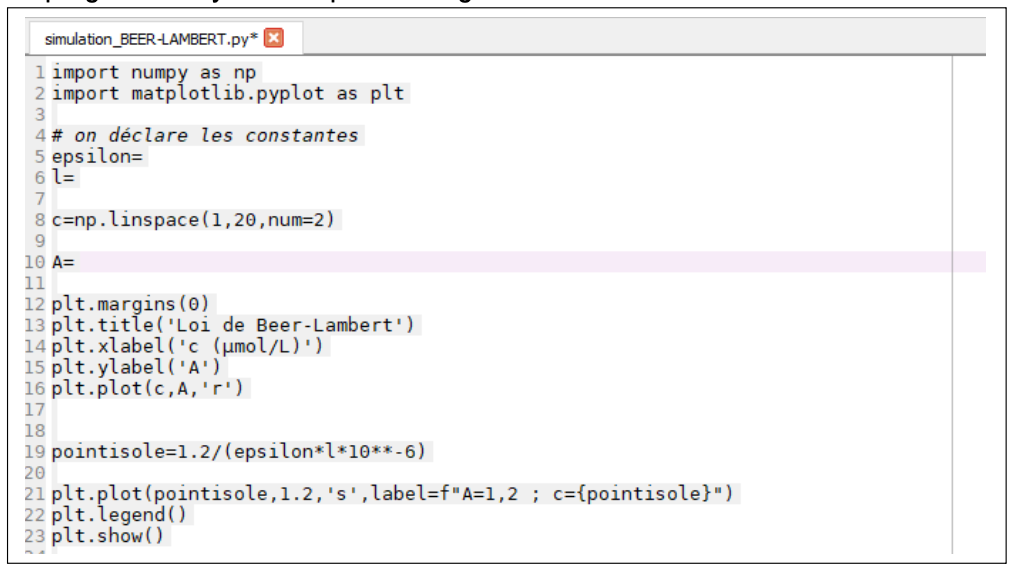
Figure 6. Programme Python.

Q12. Recopier et compléter les lignes 5, 6 et 10 du code Python.

Pour les lignes 5 et 6 on entre les valeurs :

• coefficient d’extinction molaire ɛ (epsilon) de l’espèce colorée est égale à 1,00×10⁵ L·mol^–1·cm^–1 ;
• longueur l de la cuve est égale à 1,0 cm

Ligne 5 : epsilon=1.00*10**5

Ligne 6 : l=1.0

Pour la ligne 10 on entre la formule donnant l’absorbance en fonction de ɛ, l et c :

Ligne 10 : A=eplsilon*l*c

Le programme affiche également la valeur de la concentration en quantité de matière correspondant à une absorbance A = 1,20 pour un échantillon préparé en diluant 100 fois le mélange crème colorante – solution oxydante.

On considèrera que les valeurs numériques des masses volumiques de la crème et de l’oxydant sont proches de celle de l’eau, constituant majoritaire du mélange. Le mélange est préparé en réunissant des volumes égaux de crème colorante et de solution oxydante.

Le développement de la couleur se fait selon l’équation simplifiée de réaction :

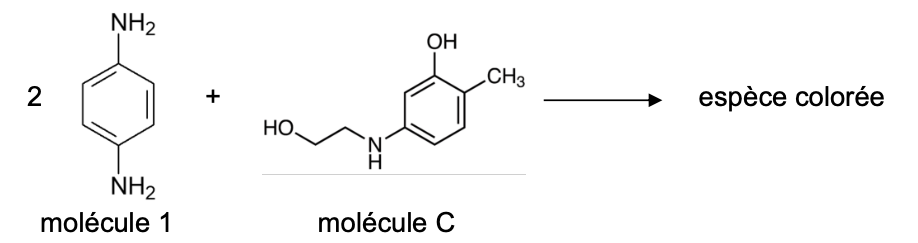
Q13. Déterminer la concentration Cc en quantité de matière de la molécule C dans le mélange.

Donnée :

• La masse molaire de la molécule C : M_C = 169 g·mol^–1.

Q14. La législation autorise jusqu’à 1,5% en masse de la molécule C dans le mélange colorant prêt à l’emploi. Vérifier que la crème colorante respecte la législation.

Le pourcentage massique est défini par :
$w=\frac{m_C}{m_{solution}}$

Or
$m_C=n_c\times M_c$

D’où
$w=\frac{n_c\times M_c}{m_{solution}}$

Or
$n_c=c_c\times V$

D’où
$w=\frac{c_c\times V\times M_c}{m_{solution}}$

Or
$m_{solution}=\rho_{solution}\times V$

D’où
$w=\frac{c_c\times V\times M_c}{\rho_{solution}\times V}$
$w=\frac{c_c\times M_c}{\rho_{solution}}$

D’après l’énoncé : « On considèrera que les valeurs numériques des masses volumiques de la crème et de l’oxydant sont proches de celle de l’eau » soit $\rho_{solution}=\rho_{eau}=1000\ g.L^{-1}$

$w=\frac{1,20\times {10}^{-3}\times 169}{1000}$
$w=2,02\times {10}^{-4}$
$w=0,0202%$

La législation autorise jusqu’à $1,5%$ en masse de la molécule C dans le mélange colorant prêt à l’emploi. Le pourcentage en masse de la molécule C est inférieur à cette valeur limite. Ainsi, la crème colorante respecte la législation.

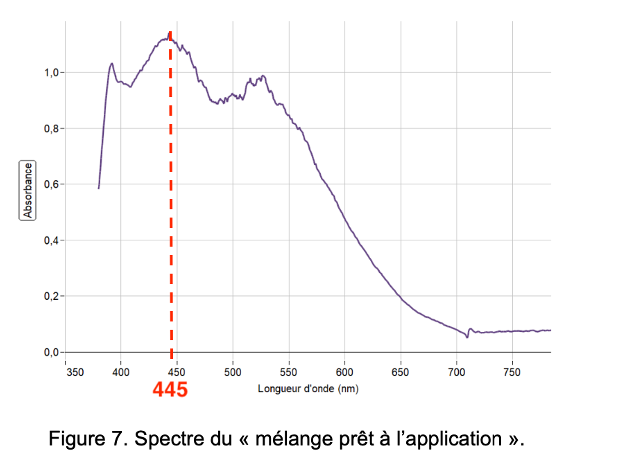
On enregistre, figure 7, le spectre du « mélange prêt à l’application » après le développement de la couleur.

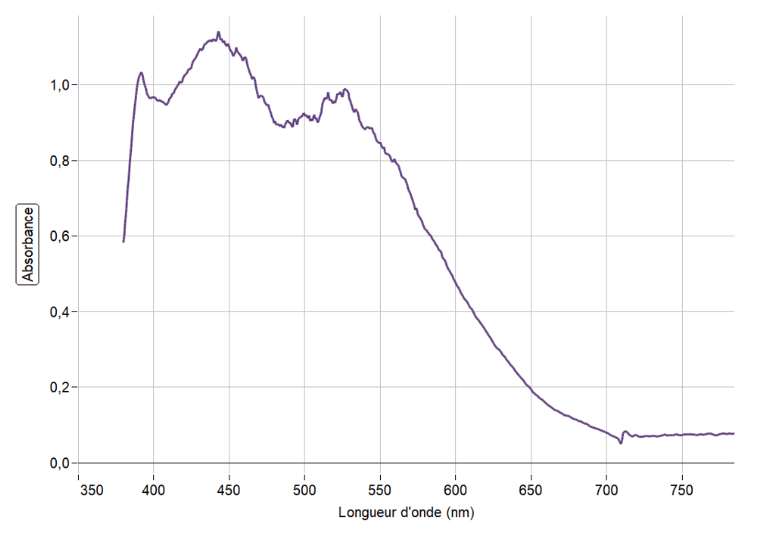
Figure 7. Spectre du « mélange prêt à l’application ».

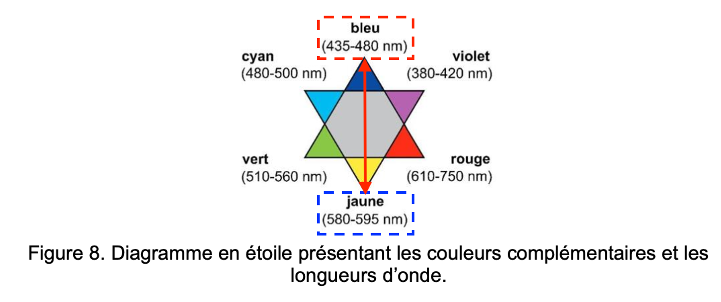
Sur le diagramme en étoile de la figure 8 les couleurs complémentaires sont diamétralement opposées.

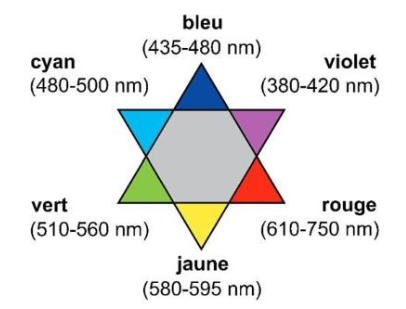
Figure 8. Diagramme en étoile présentant les couleurs complémentaires et les longueurs d’onde.

Q15. À l’aide des figures 7 et 8, déterminer la couleur principalement absorbée et en déduire la couleur dominante du mélange « mélange prêt à l’application ».

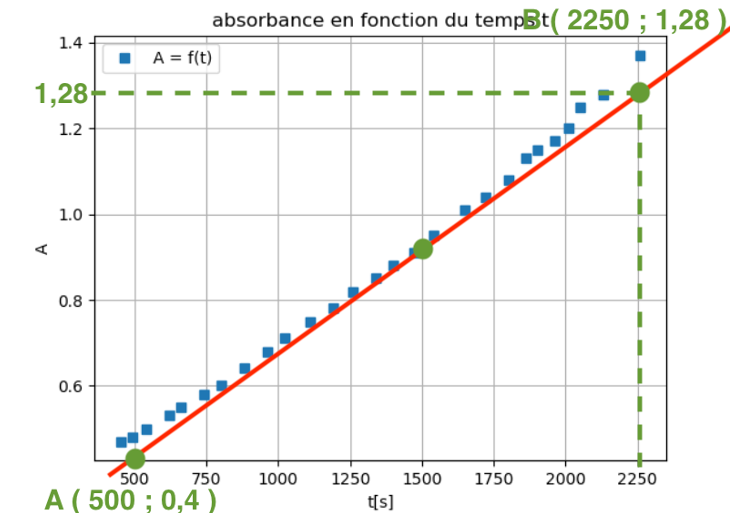
On suit l’évolution de l’absorbance en fonction du temps, la courbe obtenue est donnée figure 9.

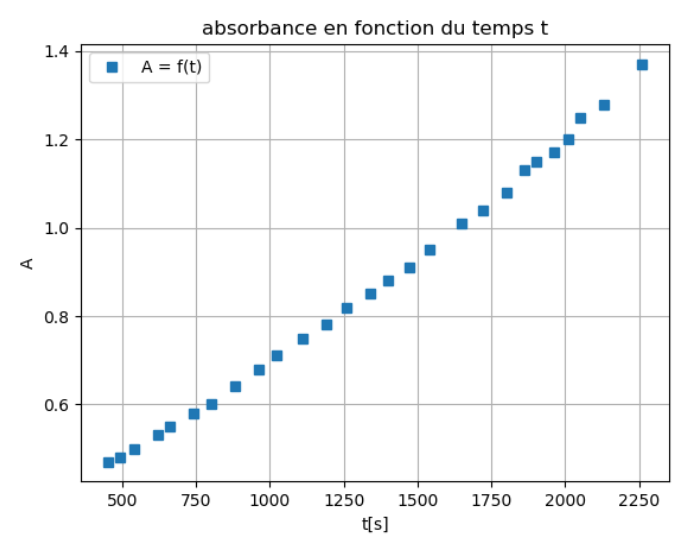
Figure 9. Représentation graphique de l’absorbance en fonction du temps pour le mélange colorant dilué au centième.

Q16. Donner la définition de la vitesse d’apparition du produit coloré, notée v_produit.

Définition de la vitesse d’apparition du produit coloré, notée $v_{produit}$ :
$v_{produit}=\frac{dc}{dt}$

Q17. À partir de l’expression de la loi de Beer-Lambert, montrer que l’expression de la vitesse d’apparition du produit coloré est : $v_{produit}=\frac{1}{\varepsilon\cdot \ell}\cdot\frac{dA}{dt}$

Données :

• La valeur de la longueur l de la cuve est égale à 1,0 cm ;
• La valeur du coefficient d’extinction molaire ε de l’espèce colorée est égale à 1,00×10⁵ L·mol^–1·cm^–1.

$v_{produit}=\frac{dc}{dt}$

Or
$A=\varepsilon\times l\times c$
$\varepsilon\times l\times c=A$
$c=\frac{A}{\varepsilon\times l}$

d’ou
$v_{produit}=\frac{d\left(\frac{A}{\varepsilon\times l}\right)}{dt}$
$v_{produit}=\frac{d\left(\frac{1}{\varepsilon\times l}\times A\right)}{dt}$

Or $\frac{1}{\varepsilon\times l}$ est constant, on peut le sortir de la dérivée :

$v_{produit}=\frac{1}{\varepsilon\times l}\times \frac{d\left(A\right)}{dt}$

Q18. Déterminer la vitesse d’apparition du produit v₁₅₀₀ à la date 1500 s.