Contrôle de l’ordre d’une réaction

Bac Asie 2023 Sujet 1

Exercice 2 – (4,5 points) –  Durée 0h47 – Calculatrice autorisée

Sujet n°23-PYCJ1JA1

Sujet et corrigé

EXERCICE II ‒ CONTRÔLE DE L’ORDRE D’UNE REACTION (4,5 points)

Le peroxyde d’hydrogène a pour formule H₂O₂. Une solution aqueuse de peroxyde d’hydrogène est appelée communément « eau oxygénée » et est utilisée comme désinfectant et détachant. En solution aqueuse, le peroxyde d’hydrogène peut se décomposer en eau et en dioxygène.

L’équation de la réaction de cette décomposition, appelée dismutation, s’écrit :

2 H₂O_{2 (aq)} → O_{2 (g)} + 2 H₂O _(ℓ)             (équation 1)

L‘objectif de cet exercice est de vérifier que la dismutation du peroxyde d’hydrogène suit une loi de vitesse d’ordre 1.

La dismutation de l’eau oxygénée est lente mais peut être accélérée en utilisant des ions fer (III), Fe³⁺. Dans ce cas, la réaction peut être décomposée en deux étapes rapides :

Étape ①        H₂O_{2 (aq)} + 2 Fe³⁺_(aq)    →        2 Fe²⁺_(aq) + O_{2 (g)} + 2 H⁺_(aq)

Étape ②        H₂O_{2 (aq)} + 2 Fe²⁺_(aq) + 2 H⁺_(aq) →        2 Fe³⁺_(aq) + 2 H₂O _(ℓ)

1. En analysant les étapes ① et ② de la dismutation du peroxyde d’hydrogène en présence d’ions fer, justifier que l’ion fer Fe³⁺ joue un rôle de catalyseur.

étape 1
$$H_2O_{2(aq)}+2{{\rm Fe}^{3+}}{(aq)}\rightarrow2{{\rm Fe}^{2+}}{(aq)}+O_{2(aq)}+2{H^+}{(aq)}$$
étape 2
$$H_2O{2(aq)}+2{{\rm Fe}^{2+}}{(aq)}+2{H^+}{(aq)}\rightarrow2{{\rm Fe}^{3+}}{(aq)}+2H_2O{(l)}$$

Equation globale : étape 1+ étape 2
$$H_2O_{2(aq)}+2{{\rm Fe}^{3+}}{(aq)}+H_2O{2(aq)}+2{{\rm Fe}^{2+}}{(aq)}+2{H^+}{(aq)}\rightarrow2{{\rm Fe}^{2+}}{(aq)}+O{2(aq)}+2{H^+}{(aq)}+2{{\rm Fe}^{3+}}{(aq)}+2H_2O_{(l)}$$
$$H_2O_{2(aq)}+2{{\rm Fe}^{3+}}{(aq)}+H_2O{2(aq)}+2{{\rm Fe}^{2+}}{(aq)}+2{H^+}{(aq)}\rightarrow2{{\rm Fe}^{2+}}{(aq)}+O{2(aq)}+2{H^+}{(aq)}+2{{\rm Fe}^{3+}}{(aq)}+2H_2O_{(l)}$$
$$H_2O_{2(aq)}+H_2O_{2(aq)}\rightarrow O_{2(aq)}+2H_2O_{(l)}$$

$$2H_2O_{2(aq)}\rightarrow O_{2(aq)}+2H_2O_{(l)}$$
Un catalyseur est une espèce qui augmente la vitesse d’une transformation, sans figurer dans l’équation de la réaction.
L’ion fer ${\rm Fe}^{3+}$ est un réactif de l’étape 1 et un produit de l’étape 2 : il ne figure pas dans le bilan de la réaction.
De plus, l’ion fer ${\rm Fe}^{3+}$ permet d’accélérer la réaction.
L’ion fer ${\rm Fe}^{3+}$ est donc un catalyseur

Pour suivre l’évolution temporelle de la concentration en H₂O₂ en présence de Fe³⁺, on réalise le dosage par titrage, à différentes dates t, d’un échantillon du milieu réactionnel par des ions permanganate MnO₄^– d’une solution de permanganate de potassium acidifiée. Chaque dosage par titrage permet de déterminer la concentration [H₂O₂] en peroxyde d’hydrogène restant à la date t.

L’équation de la réaction support du dosage est :

5 H₂O_{2 (aq)} + 2 MnO₄^–_(aq) + 6 H⁺_(aq) → 5 O_2(g) + 2 Mn²⁺_(aq) + 8 H₂O_(ℓ)  (équation 2)

La seule espèce chimique colorée est l’ion permanganate MnO₄^–, rose-violet en solution aqueuse. L’équivalence est donc repérée par un changement de couleur du milieu réactionnel.

Protocole de suivi cinétique de la décomposition de l’eau oxygénée : On dispose : – d’une solution S0 d’eau oxygénée de concentration en peroxyde d’hydrogène [H2O2]0 inconnue ; – d’une solution de chlorure de fer (III) (Fe3+ ; 3 Cℓ –) de concentration 0,10 mol∙L-1 ; – d’une solution SP de permanganate de potassium (K+ ; MnO4–) dont la concentration est CP = 2,00 × 10-2 mol∙L-1 ; – d’une solution d’acide sulfurique. Préparation du dispositif de dosage par titrage • Remplir la burette graduée de la solution Sp de permanganate de potassium (K+ ; MnO4–) • Préparer sept erlenmeyers contenant chacun 40 mL d’eau distillée glacée et 10 mL de solution d’acide sulfurique. • Placer ces sept erlenmeyers dans un cristallisoir contenant un mélange d’eau et de glace. Préparation du mélange réactionnel • Dans un erlenmeyer de 150 mL, verser 95,0 mL de la solution S0 d’eau oxygénée.Introduire un barreau aimanté. • Placer l’ensemble sur un agitateur. • Mettre en route l’agitation.Verser rapidement 5 mL de solution de chlorure de fer (III) (Fe3+ ; 3 Cℓ –) et déclencher immédiatement le chronomètre. Dosage : détermination de la concentration en H2O2 à différentes dates t • Le plus rapidement possible, prélever un volume VR = 10,0 mL du milieu réactionnel. • Verser rapidement ce prélèvement dans l’un des sept erlenmeyers. • Introduire un barreau aimanté et doser par titrage le peroxyde d’hydrogène présent dans le volume VR à cette date t par la solution de permanganate SP.N • oter VE le volume équivalent alors versé. • Procéder de la même façon aux dates 4 min, 6 min, 8 min, 12 min, 20 min, 30 min, 40 min et 80 min.

Résultats expérimentaux

t (min)	1,75	4,0	6,0	8,0	12,0	20,0	30,0	40,0	80,0
VE (mL)	16,0	15,0	13,8	12,9	11,4	8,6	5,9	4,2	1,2
[H2O2] (mmol∙L-1)	80,0	75,0	69,0	64,5		43,0	29,5	21,0	6,0

2. Identifier les deux facteurs cinétiques mis en œuvre pour stopper la réaction de dismutation (équation 1) le temps du dosage.

Les sept erlenmeyers contiennent de l’eau distillée glacée :

• L’eau distillée permet de diluer le prélèvement et ainsi diminuer la concentration et donc la vitesse de réaction.
• Le fait que l’eau soit glacée permet de diminuer la température et donc la vitesse de réaction.

Ces deux facteurs cinétiques sont mis en œuvre pour stopper la réaction de dismutation le temps du dosage.

3. Indiquer le changement de couleur observé à l’équivalence (équation 2).

La seule espèce chimique colorée est l’ion permanganate.
Avant l’équivalence, le permanganate est le réactif limitant. La solution reste incolore.
Après l’équivalence, le permanganate est le réactif en excès. La solution devient rose-violet.

A l’équivalence on observe un changement de couleur de l’incolore au rose-violet.

4. À partir de l’équation de la réaction support du dosage, équation 2, et de la définition de l’équivalence, établir que la concentration en quantité de matière du peroxyde d’hydrogène est donnée par la relation suivante :

$$\left[H_2O_2\right]=\frac{5\times C_P\times V_E}{2\times V_R}$$

$$5H_2O_{2(aq)}+2{{\rm MnO}4^-}{(aq)}+6{H^+}{(aq)}\rightarrow 5O{2(aq)}+2{{\rm Mn}^{2+}}{(aq)}+8H_2O{(l)}$$
A l’équivalence, les réactifs ont été introduits dans les proportions stœchiométrique :

$$\frac{n_{H_2O_2}^i}{5}=\frac{n_{{\rm MnO}_4^-}^{eq}}{2}$$
$$\frac{\left[H_2O_2\right]\times V_R}{5}=\frac{C_p\times V_E}{2}$$
$$\left[H_2O_2\right]=\frac{5\times C_p\times V_E}{2\times V_R}$$

5. Calculer la valeur de [H₂O₂] manquante à la date t = 12 min dans le tableau des résultats expérimentaux.

$$\left[H_2O_2\right]=\frac{5\times C_p\times V_E}{2\times V_R}$$
$$\left[H_2O_2\right]=\frac{5\times 2,00\times {10}^{-2}\times 11,4\times {10}^{-3}}{2\times 10,0\times {10}^{-3}}$$
$$\left[H_2O_2\right]=5,70\times {10}^{-2}\ mol.L^{-1}$$
$$\left[H_2O_2\right]=57,0\times {10}^{-3}\ mol.L^{-1}$$
$$\left[H_2O_2\right]=57,0\ mmol.L^{-1}$$

6. A partir de la définition  de la vitesse de disparition de l’eau oxygénée, et en supposant que la dismutation du peroxyde d’hydrogène suit une loi cinétique d’ordre 1, retrouver la relation suivante :

$$\frac{d\left[H_2O_2\right]}{dt}=-k\times\left[H_2O_2\right]$$

$$v_d=-\frac{d\left[H_2O_2\right]}{dt}$$
Dans le cas d’une loi de vitesse d’ordre 1 : $$v_d=k\times \left[H_2O_2\right]$$
$$-\frac{d\left[H_2O_2\right]}{dt}=k\times \left[H_2O_2\right]$$
$$\frac{d\left[H_2O_2\right]}{dt}=-k\times \left[H_2O_2\right]$$

La relation ci-dessus, question 6, est une équation différentielle qui admet des solutions de la forme :

$\left[H_2O_2\right]_{\left(t\right)}=B\times e^{-k\times t}$ (relation 1)

7. Donner la signification physique de B.

$$\left[H_2O_2\right]{\left(t\right)}=B\times e^{-k\times t}$$
A instant initial :
$$\left[H_2O_2\right]{\left(t=0\right)}=B\times e^{-k\times 0}$$
$$\left[H_2O_2\right]{\left(t=0\right)}=B\times 1$$
$$\left[H_2O_2\right]{\left(t=0\right)}=B$$

B est la concentration en peroxyde d’hydrogène initiale.

À partir des résultats expérimentaux obtenus, on a tracé les deux graphiques ci-après (figure 1 et figure 2).

[H₂O₂] (en mmol∙L^-1)

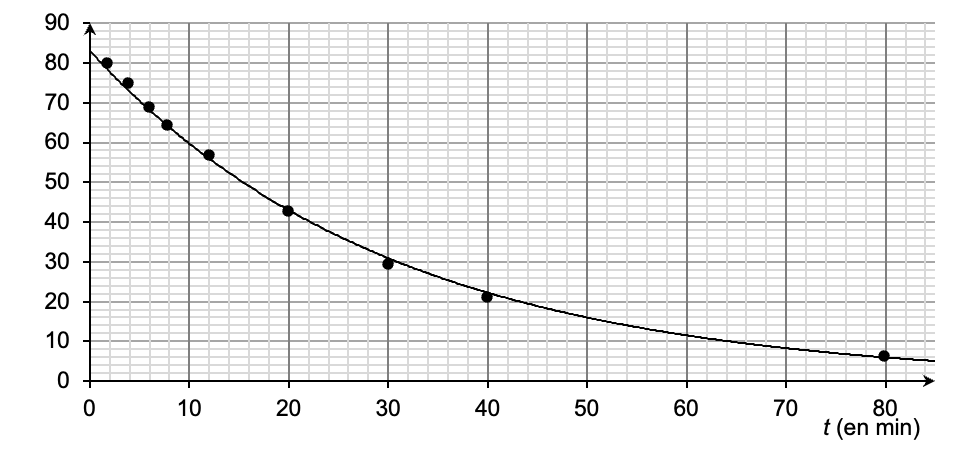
Figure 1 – Évolution temporelle de la concentration de H₂O₂

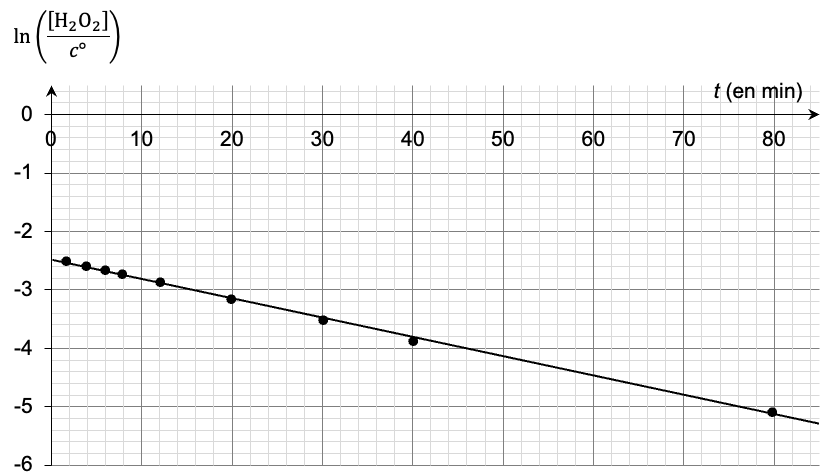
Figure 2 – Évolution temporelle de $\ln\left(\frac{\left[H_2O_2\right]}{c^\circ}\right)$ avec [H₂O₂] en mol∙L^-1 et c° = 1 mol∙L^-1

Compte tenu des propriétés de la fonction logarithme népérien, il est possible d’écrire à partir de la relation 1 :

$\ln\left(\frac{\left[H_2O_2\right]}{c^\circ}\right)=\ln\left(\frac{B}{c^\circ}\right)-k\times t$ (relation 2)

8. En s’appuyant sur la relation 2 et le graphique de la figure 2, montrer que l’hypothèse selon laquelle la dismutation du peroxyde d’hydrogène suit une loi cinétique d’ordre 1 est bien valide. En déduire la valeur de la constante k.

Dans le cas d’une loi de vitesse d’ordre 1, on obtient la relation (2) suivante :
$$\ln\left[\frac{\left[H_2O_2\right]}{c^0}\right]=\ln\left[\frac{B}{c^0}\right]-kt$$

$$\ln(R)$$ est une fonction affine décroissante (le coefficient directeur est négatif).

Expérimentalement, on obtient une droite qui ne passe pas par l’origine : c’est une fonction affine du type $$\ln\left[\frac{\left[H_2O_2\right]}{c^0}\right]=at+b$$, avec a le coefficient directeur.

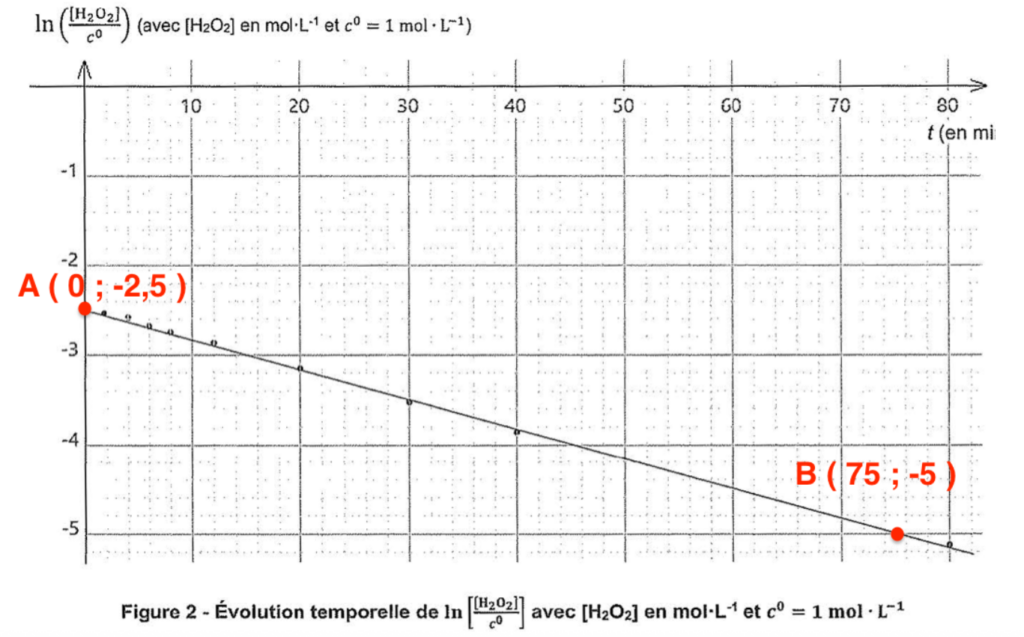
L’hypothèse selon laquelle la dismutation du peroxyde d’hydrogène suit une loi cinétique d’ordre 1 est bien valide.

« a » est le coefficient directeur de la droite :
$$a=\frac{y_B-y_A}{x_B-x_A}$$
$$a=\frac{-5-\left(-2,5\right)}{75-0}=-3,3.{10}^{-2}\min^{-1}$$
$$k=-a$$
$$k=3,3.{10}^{-2}\min^{-1}$$

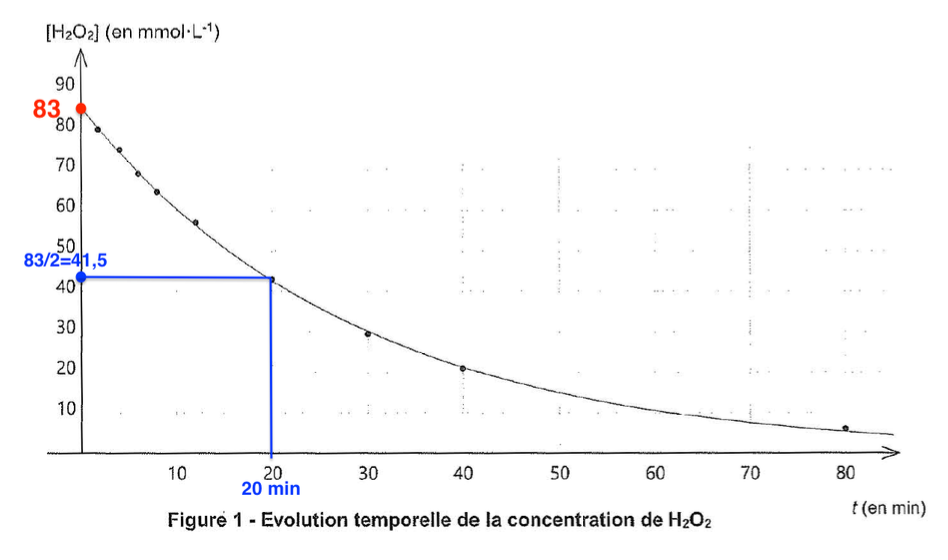
9. Définir puis déterminer le temps de demi-réaction t_1/2 de cette réaction de dismutation à l’aide de la figure 1.

$$t_{1/2}$$ est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : $$x(t_{1/2}) = x_f/2$$.

$$\left[H_2O_2\right]{\left(t=t{1/2}\right)}=\frac{\left[H_2O_2\right]_i}{2}$$

Pour une réaction qui suit une cinétique d’ordre 1, on peut montrer que le temps de demi-réaction t_1/2 est indépendant de la concentration initiale et est relié à la grandeur k par la relation suivante :

$$k\times t_{1/2}=\ln(2)$$

10. Préciser si la valeur de la grandeur k varie si la concentration initiale [H₂O₂]₀ diminue.

$$k\times t_{1/2}=\ln{\left(2\right)}$$
$$k=\frac{\ln{\left(2\right)}}{t_{1/2}}$$
Or d’après l’énoncé, pour une réaction qui suit une cinétique d’ordre 1, $t_{1/2}$ est indépendant de la concentration initiale. Ainsi, $k$ qui ne dépend que de $t_{1/2}$ est indépendant de la concentration initiale $\left[H_2O_2\right]_0$.
Ainsi, si $\left[H_2O_2\right]_0$ diminue, $k$ reste inchangé.