Nouvelle Calédonie 2025 Sujet 1

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°25-PYCJ1NC1

EXERCICE 1 – DE L’ASPIRINE POUR FAVORISER L’ÉCOULEMENT SANGUIN (9 points)

L’aspirine ou acide acétylsalicylique est fréquemment employée dans le cas d’un traitement préventif de certaines maladies cardiovasculaires (infarctus du myocarde, accident vasculaire cérébral, etc.) pour sa capacité à fluidifier le sang. Toutefois, elle produit des effets irritants sur l’estomac.

L’aspirine existe sous la forme de comprimés ayant un enrobage gastro-résistant pour les traitements de longue durée.

Lorsque survient un accident ischémique* transitoire (ou AIT), l’aspirine sans enrobage peut être donnée par une prise urgente d’une dose de charge comprise entre 160 et 300 mg.

* Ischémie : diminution de l’apport sanguin.

Données :

• Masse molaire de l’aspirine : M = 180 g·mol^–1.
• Formule brute de l’aspirine : C₉H₈O₄.
• pKA du couple C₉H₈O₄/C₉H₇O₄^– : pK_A = 3,5 à 25 °C.

Les différentes parties de cet exercice peuvent être traitées indépendamment les unes des autres.

Partie A – À propos de l’aspirine

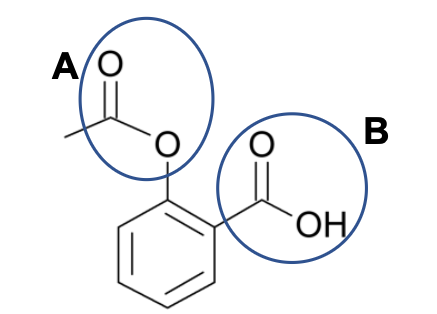
Figure 1 – Formule topologique de l’aspirine

1. Nommer les groupes caractéristiques A et B entourés sur la figure 1.

Groupe caractéristique A : Carboxyle (non demandé : famille des ester)
Groupe caractéristique B : Carboxyle (non demandé : famille des acides carboxyliques).

2. Écrire    l’équation    de    la    réaction    modélisant    la transformation acide-base de l’aspirine avec l’eau.

$C_9H_8O_4(aq)+H_2O(l)\rightleftarrows C_9H_7O_4^-(aq)+H_3O^+(aq)$

3. À l’aide d’un diagramme de prédominance associé à ce couple, déterminer la forme prédominante dans l’estomac, dont le pH est compris entre 1 et 3.

Diagramme de prédominance :

Pour $1<pH<3$ : $pH$ est inférieur à $pKA$
$C_9H_8O_4$ est l’espèce prédominante dans l’estomac.

4. Expliquer pourquoi un comprimé avec enrobage est préférable à un comprimé sans enrobage pour un traitement de longue durée.

Dans l’estomac, la forme acide du principe actif est prédominante. L’enrobage empêche sa libération au niveau gastrique, ce qui évite la formation d’ions $H_3O^+$ et la diminution du pH. Cela limite les irritations et les lésions de l’estomac, ce qui est préférable lors d’un traitement de longue durée.

Partie B – Titrage d’un comprimé

On dispose d’un comprimé d’Aspirine du Rhône©. Il s’agit d’une formulation sans enrobage. On désire savoir si ce comprimé pourrait convenir à une dose de charge dans le cas d’un AIT.

Pour cela, on met en œuvre le protocole expérimental suivant :

• dans un mortier et à l’aide d’un pilon, broyer le comprimé d’Aspirine du Rhône ;
• préparer un volume V = 500,0 mL de solution, notée S, en dissolvant la poudre d’aspirine ainsi obtenue dans de l’eau distillée ;
• prélever un volume V_A = 20,0 mL de la solution S ;
• titrer avec une solution d’hydroxyde de sodium (Na⁺(aq) + HO^–(aq)), de concentration en quantité de matière C_B = 1,0 × 10^{– 2} mol∙L^-1, en réalisant un suivi pH-métrique.

Les courbes de la figure 2 ci-après représentent l’évolution du pH et la dérivée du pH en fonction du volume V_B d’hydroxyde de sodium (Na⁺(aq) + HO^–(aq)) versé au cours du titrage.

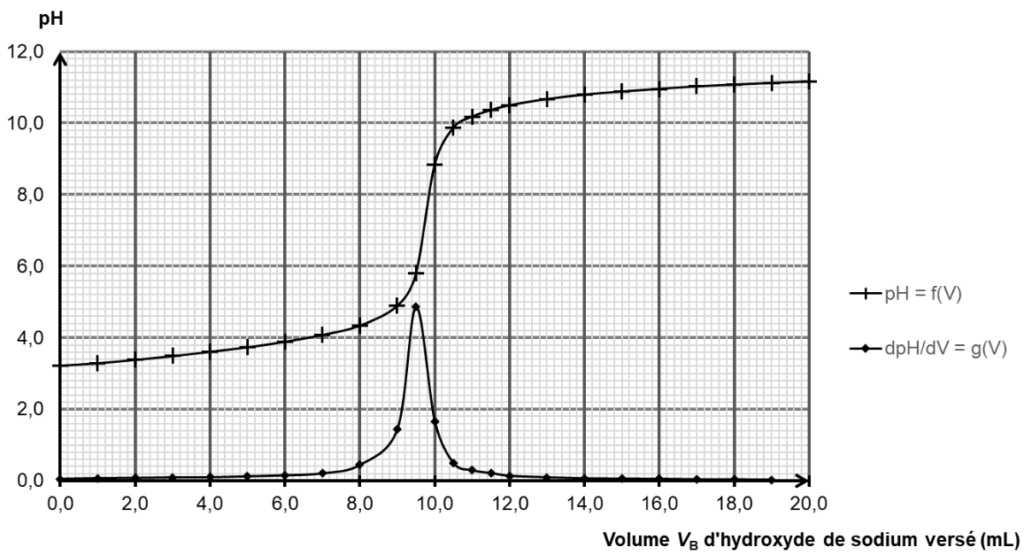
Figure 2 – Évolution du pH et de sa dérivée en fonction du volume VB d’hydroxyde de sodium (Na⁺(aq) + HO^–(aq)) versé au cours du titrage

L’équation de la réaction acide-base support de ce titrage s’écrit :

C₉H₈O₄(aq) + HO^–(aq) → C₉H₇O₄^–(aq) + H₂O(𝓁)

5. Exploiter la courbe de titrage de la figure 2 pour déterminer la masse m_A d’aspirine contenue dans le comprimé testé.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti : la démarche est évaluée et nécessite d’être correctement présentée.

$C_9H_8O_4(aq)+{\rm HO}^-(aq)\rightleftarrows C_9H_7O_4^-(aq)+H_2O(l)$

A l’équivalence :
$\frac{n_{C_9H_8O_4}^i}{1}=\frac{n_{{\rm HO}^-}^{eq}}{1}$

$n_0(C_9H_8O_4)=n_e({\rm HO}^-)$

$C_A\times V_A=C_B\times V_E$
$C_A=\frac{C_B\times V_E}{V_A}$

$C_A=\frac{1,00\times 10^{-2}\times 9,5\times 10^{-3}}{20,0\times 10^{-3}}$
$C_A=4,8\times 10^{-3}\ mol.L^{-1}$

Déterminons la masse d’aspirine contenue dans le comprimé testé.

$n_A=\frac{m_A}{M_A}$
$\frac{m_A}{M_A}=n_A$
$m_A=n_A\times M_A$

Or
$C_A=\frac{n_A}{V}$
$\frac{n_A}{V}=C_A$
$n_A=C_A\times V$
D’où
$m_A=C_A\times V\times M_A$
$m_A=4,8\times 10^{-3}\times 500,0\times 10^{-3}\times 180$
$m_A=0,432\ g$
$m_A=432\ mg$

6. Indiquer si la quantité d’aspirine contenue dans ce comprimé est adaptée, sous-dosée ou surdosée, pour une prise urgente, dans le cas d’un AIT. Justifier.

D’après le sujet : « Lorsque survient un accident ischémique* transitoire (ou AIT), l’aspirine sans enrobage peut être donnée par une prise urgente d’une dose de charge comprise entre 160 et 300 mg. »
La masse d’aspirine dans le comprimé est de 430 mg
Ainsi, la quantité d’aspirine contenue dans ce comprimé est surdosée, pour une prise urgente, dans le cas d’un AIT.

Partie C – Étude de la cinétique de l’hydrolyse de l’aspirine

La stabilité d’un médicament dans différents milieux et conditions expérimentales est étudiée en pharmacologie.

On se propose d’étudier la cinétique de la transformation entre l’aspirine et l’eau, à température ambiante. Cette transformation lente forme de l’acide salicylique C₇H₆O₃ et de l’acide éthanoïque C₂H₄O₂.

La réaction entre l’aspirine et l’eau est appelée hydrolyse de l’aspirine et a pour équation de réaction :

C₉H₈O₄(aq) + H₂O(𝓁)  ⇌  C₇H₆O₃(aq) + C₂H₄O₂(aq)

L’hydrolyse de l’aspirine est suivie par spectrophotométrie en présence d’un excès de chlorure de fer III, FeCl₃(aq). En effet, ce dernier réagit avec l’acide salicylique pour former une espèce chimique violette.

On considère que :

• l’absorbance du mélange à la longueur d’onde choisie ne dépend que de la concentration en acide salicylique ;
• l’eau étant en excès, la réaction d’hydrolyse de l’aspirine est totale.

On mesure l’absorbance du mélange au cours du temps, à température constante, et on en déduit l’évolution temporelle de la concentration en quantité de matière C de l’aspirine représentée sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11.

7. Définir la vitesse volumique de disparition de l’aspirine.

La vitesse volumique de disparition $v_{d,A}$ de l’aspirine est définie par :
$v_{d,A}=-\frac{d\left[A\right]}{dt}$

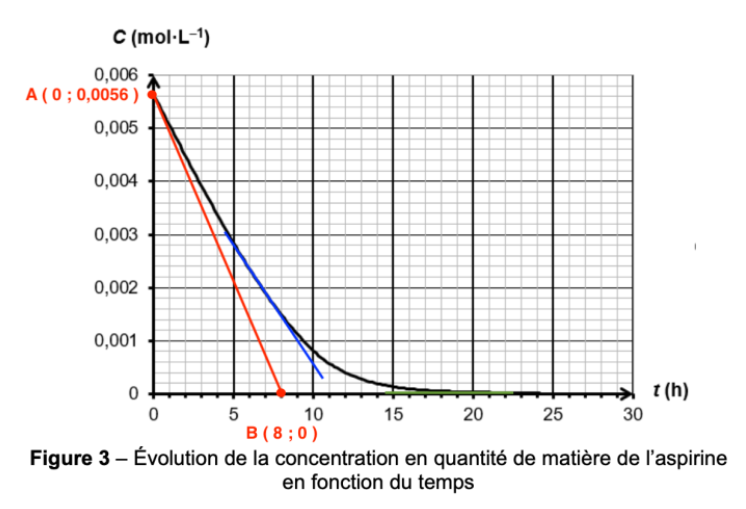
8. Déterminer la vitesse volumique de disparition de l’aspirine à la date t = 0 h en faisant apparaître la construction employée sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11.

$v_{d,A}=-\frac{d\left[A\right]}{dt}$
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.

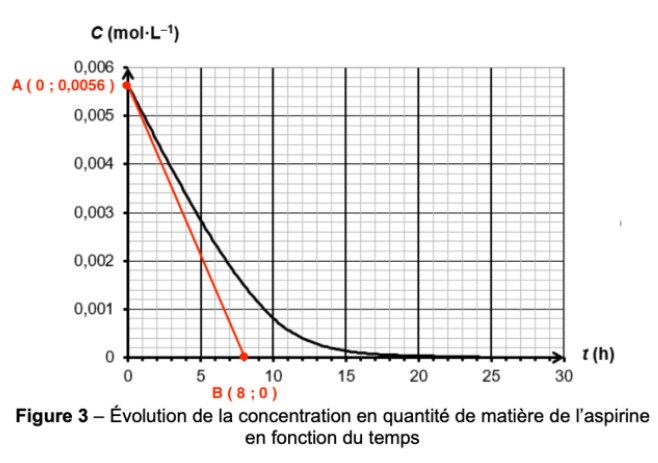
9. Justifier sans calcul, à l’aide de la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, comment évolue la vitesse volumique de disparition de l’aspirine au cours du temps.

On donne ci-dessous, figure 4, un extrait du code Python permettant de tracer la courbe de la figure 5 représentant les valeurs de vitesse volumique de disparition de l’aspirine, notée v, en fonction de la concentration C de l’aspirine.

Le temps t est exprimé en heures (h), la concentration C de l’aspirine en mol·L^–1 et les valeurs de vitesse volumique v de disparition de l’aspirine en mol·L^–1·h^–1.

1	import matplotlib.pyplot as plt
2
3	# Pour des raisons de clarté, l’ensemble des valeurs des listes suivantes
4	# qui correspondent à la figure 3 ne sont pas intégralement explicitées
5	t = [0.0, 0.167, 0.333, 0.5, 0.667, 0.833, 1.0, …]
6	C = [0.00562, 0.00553, 0.00543, 0.00534, 0.00525, 0.00515, 0.00506, …]
7
8	v = [] # Création d’une liste vide pour les valeurs de vitesse
9
10	# Remplissage de la liste donnant la vitesse v
11	for i in range(len(t) – 1):   # len(t) – 1 car la vitesse ne peut pas être
12	# calculée pour la dernière valeur de t
13	v.append(………………………)      # Calcul de la vitesse à la date t[i] sachant
14	# que la fonction append permet d’ajouter une
15	# valeur en fin de liste

Figure 4 – Extrait du code Python utilisé (avec des passages non explicités)

On assimile la vitesse volumique de disparition de l’aspirine v, à une date t, à sa vitesse moyenne de disparition entre deux dates t successives t_i et t_i+1.

10. Recopier et compléter la ligne 13 du code Python (figure 4) visant à calculer chaque valeur de v et à l’ajouter en fin de liste v.

v.append(-(C[i+1] – C[i]) / (t[i+1] – t[i]))# Calcul de la vitesse à la date t[i] sachant

$v_{d,A}=-\frac{d\left[A\right]}{dt}$
$v_{d,A}=-\frac{\Delta [A]}{\Delta t}$

C[i+1]-C[i] représente la variation de concentration,
t[i+1]-t[i] représente la variation de temps (en heures),
le signe moins permet d’obtenir une vitesse positive pour une disparition.

Grâce au code Python, on sélectionne quelques valeurs de la vitesse volumique de disparition v de l’aspirine et on les représente en fonction de la concentration C en aspirine sur la figure 5 suivante.

11. Justifier, à l’aide de la figure 5 suivante, que l’hydrolyse de l’aspirine ne suit pas une loi de vitesse d’ordre 1 par rapport à l’aspirine dans les conditions de l’expérience.

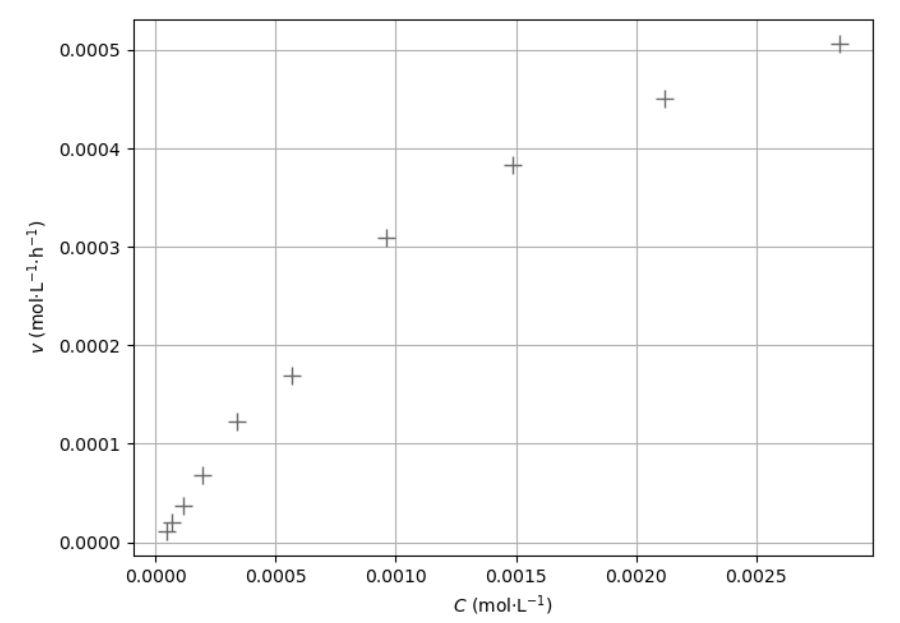
Figure 5 – Des valeurs de v en fonction de C

Le mécanisme réactionnel de l’hydrolyse de l’aspirine comporte plusieurs étapes. Sur la figure 6 suivante, reproduite dans l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, on donne la première étape simplifiée de ce mécanisme réactionnel :

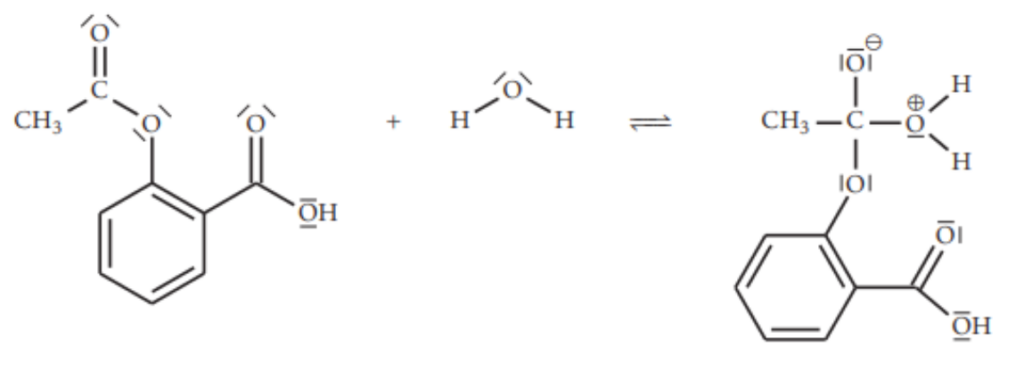
Figure 6 – Première étape simplifiée du mécanisme réactionnel de l’hydrolyse de l’aspirine

12. Entourer et nommer, sur la figure 6 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, le site donneur et le site accepteur de doublet d’électrons des réactifs qui interagissent lors de cette première étape.

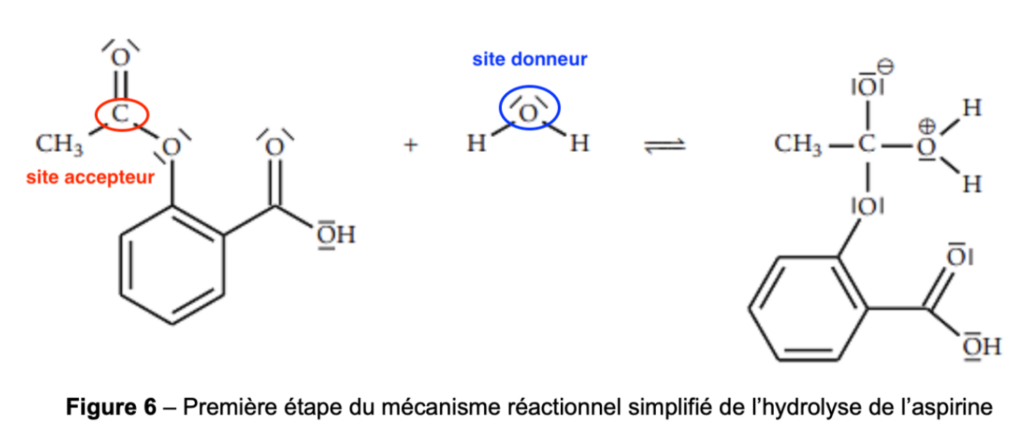
13. Représenter, sur la figure 6 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, les flèches courbes modélisant les déplacements d’électrons permettant la formation de l’intermédiaire réactionnel.

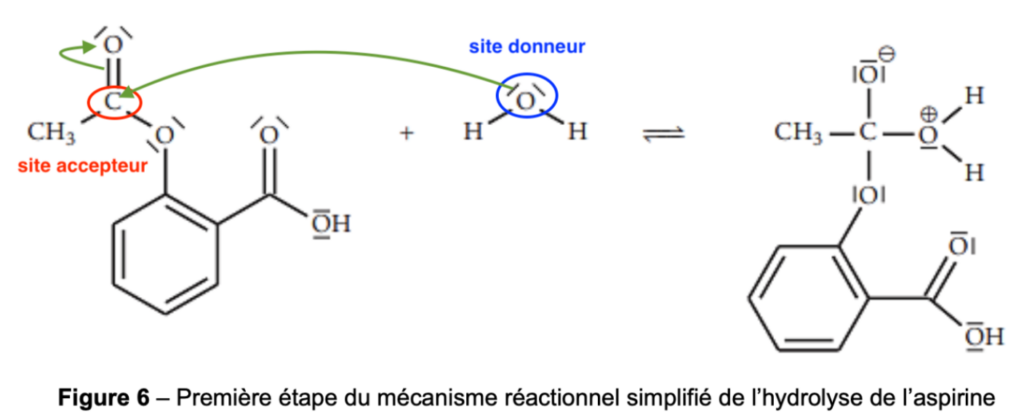
Lors d’une formation de liaison, le doublet d’électrons se déplace du site donneur vers un site accepteur.
Lors d’une rupture de liaison, la flèche part de la liaison vers l’atome le plus électronégatif.

14. Identifier, parmi les catégories suivantes, celle à laquelle appartient cette transformation : oxydoréduction, acide-base, addition, élimination, substitution.

Cette transformation est une addition.

L’hydrolyse de l’aspirine est une transformation lente.

15. Proposer une modification des conditions expérimentales permettant de diminuer la durée de cette transformation.

La vitesse de réaction dépend de :
• La concentration, plus elle est élevée, plus la vitesse de réaction est grande
• La température, plus elle est élevée, plus la vitesse de réaction est grande
• La présence d’un catalyseur, en présence d’un catalyseur la réaction est plus rapide

Ainsi, pour diminuer la durée de cette transformation on peut
• Augmenter la concentration
• Augmenter la température
• Mettre un catalyseur

Remarque : une seule modification est demandée.

ANNEXE À RENDRE AVEC LA COPIE

EXERCICE 1 – DE L’ASPIRINE POUR FAVORISER L’ÉCOULEMENT SANGUIN

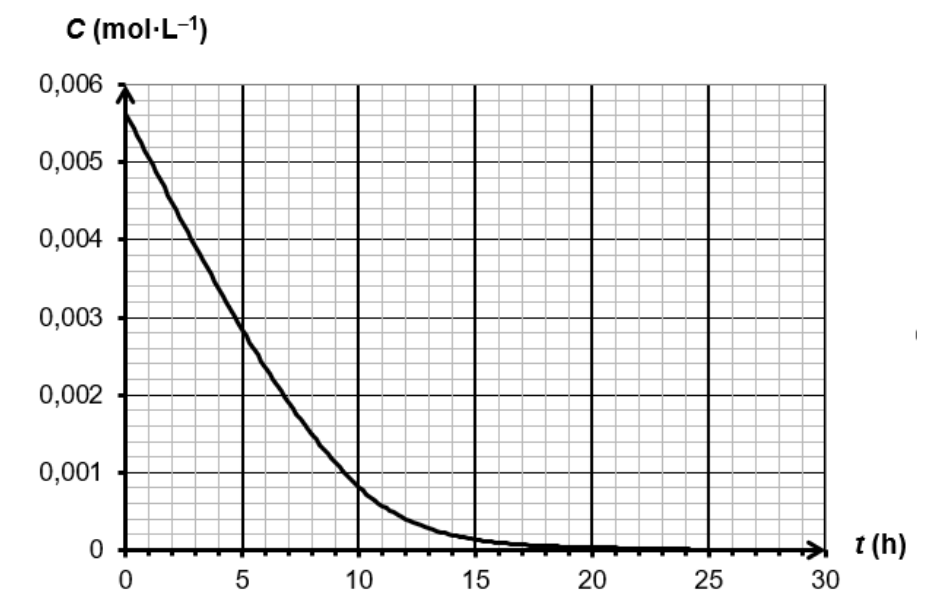
Figure 3 – Évolution de la concentration en quantité de matière de l’aspirine en fonction du temps

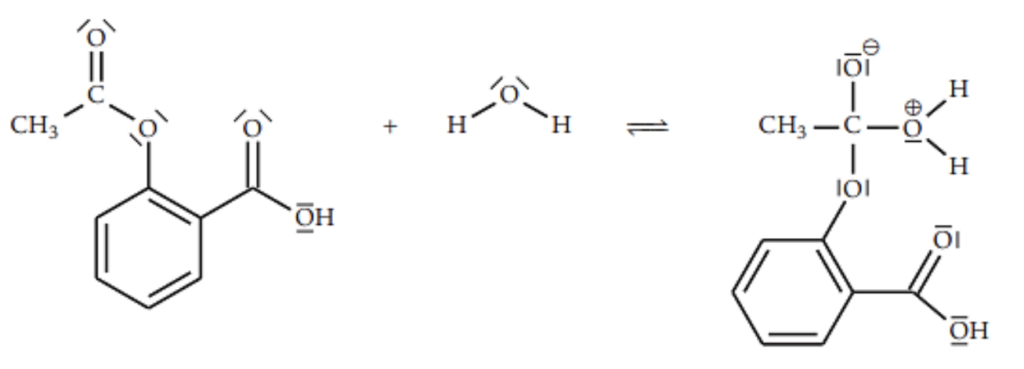
Figure 6 – Première étape du mécanisme réactionnel simplifié de l’hydrolyse de l’aspirine