Liban 2022 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ2LR1
Mots-clés : fonctionnement d’une pile ; réactions électrochimiques aux électrodes ; capacité électrique d’une pile.
La défibrillation est une méthode utilisée afin de réguler le rythme cardiaque. Elle consiste à appliquer un « choc électrique » très bref au cœur du patient. Un défibrillateur interne est un petit boîtier qui est implanté dans le thorax du patient. Il est constitué de circuits électriques alimentés par une pile au lithium qui apporte l’énergie nécessaire à son fonctionnement.
Cet exercice étudie le fonctionnement d’une pile au lithium dont un schéma est présenté ci-dessous.
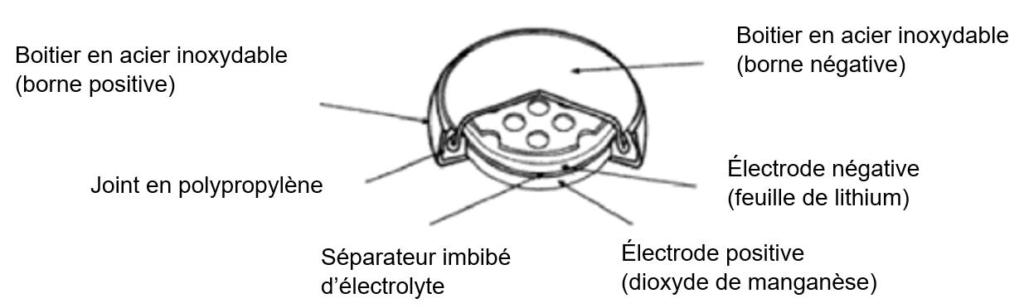
D’après générateurs électrochimiques, P. Mayé 2010
Données :
- tension à vide aux bornes de la pile au lithium : 𝑈 = 3,0 V ;
- énergie stockée dans une pile : 𝐸 = 𝑄 · 𝑈 où 𝑄 est la capacité électrique de la pile en coulomb (C) et 𝑈 la tension à vide en volt (V) à ses bornes ;
- masse de la pile : 𝑚pile = 2,9 g ;
- composition massique de la pile :
| lithium | Li | 5 % |
| dioxyde de manganèse | MnO2 | 30 % |
- couples oxydant/réducteur : Li+/Li(s) et MnO2(s)/MnO2H(s) ;
- masses molaires : 𝑀(Li) = 6,9 g⋅mol−1 et 𝑀(MnO2) = 86,9 g⋅mol−1 ;
- numéro atomique du lithium : 𝑍Li = 3 ;
- constante de Faraday : 𝐹 = 96 500 C·mol−1 ;
- constante d’Avogadro : 𝑁𝐴 = 6,022 × 1023 mol−1 ;
- charge élémentaire : 𝑒 = 1,60 × 10−19 C.
1. D’après les polarités des électrodes et les couples mis en jeu, écrire les réactions électrochimiques se produisant au niveau des électrodes quand la pile délivre un courant électrique, puis en déduire que l’équation de la réaction modélisant le fonctionnement de la pile s’écrit :
Li(s) + MnO2(s) + H+ → Li+ + MnO2H(s)
On donne un extrait du tableau périodique des éléments ci-dessous.
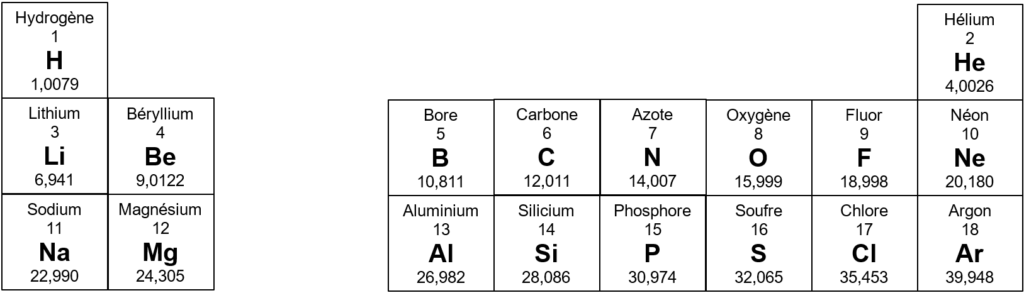
2. La configuration électronique d’un atome de lithium est 1s2 2s1. Justifier qu’un atome de lithium donne un ion monoatomique Li+. Préciser, en justifiant la réponse, si le lithium métallique est un réducteur ou un oxydant.
3. Montrer que dans la pile neuve, la quantité de matière initiale de lithium est égale à 2,1 × 10−2 mol et déterminer la quantité de matière initiale en oxyde de manganèse MnO2.
4. En déduire le réactif limitant le fonctionnement de la pile et la composition de la pile quand celle-ci est usée.
5. Définir la capacité électrique 𝑄 d’une pile et calculer sa valeur maximale pour la pile au lithium considérée.
6. Le fabricant annonce une capacité électrique réelle de 225 mAh. Proposer une cause pour rendre compte de l’écart entre la valeur maximale et la valeur réelle.
7. En utilisant la capacité électrique donnée par le fabriquant, comparer l’énergie massique de la pile au lithium utilisé dans le défibrillateur avec celles d’autres piles données dans le tableau ci-dessous. Commenter.
| Type de pile | lithium – monofluorure de carbone | zinc – argent | zinc – air | alcaline |
| Tension (V) | 3 | 1,5 | 1,2 | 6 |
| Énergie massique (J·g−1) | 1215 | 378 | 130 | 363 |
