Bac Métropole Juin 2021 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ1ME2
Sujet et corrigé
Mots-clés : titrage suivi par conductimétrie

La présence de magnésium dans le corps humain stimule l’immunité et diminue la fatigue. Bien que le magnésium soit présent dans de nombreux aliments comme les amandes, les épinards ou les bananes, il peut être prescrit en complément. Des sachets de chlorure de magnésium sont disponibles en pharmacie et permettent cet apport complémentaire en magnésium au corps humain.
La poudre présente dans le sachet est du chlorure de magnésium hydraté pur, de formule MgCℓ2, 4,5 H2O, où 4,5 est appelé le degré d’hydratation. Celui-ci représente le nombre de moles d’eau présentes dans une mole de chlorure de magnésium hydraté.
Cet exercice propose de déterminer le degré d’hydratation du chlorure de magnésium du sachet à l’aide d’un titrage suivi par conductimétrie.
Données :
- masse de poudre dans le sachet : m = 20,3 g ;
- masse molaire de l’eau : Meau = 18,0 g·mol–1 ;
- masse molaire du chlorure de magnésium MgCℓ2 : M2 = 95,3 g·mol–1 ;
- valeurs de la conductivité molaire ionique λ à 25 °C de quelques ions :
| ion | Mg2+ | Cℓ– | Ag+ | NO3– |
| λ en mS·m2·mol–1 | 10,61 | 7,63 | 6,19 | 7,14 |
Le contenu d’un sachet acheté en pharmacie est dissous en totalité pour fabriquer 1,00 L de solution aqueuse S1, la dissolution étant totale dans ces conditions. Une solution aqueuse S2 est obtenue par dilution d’un facteur cinq de la solution aqueuse S1.
1. Écrire l’équation de la réaction modélisant la dissolution de la poudre du sachet dans l’eau.
$${\rm MgCl}_2,\ 4,5H_2O_{(s)}\rightarrow{\rm Mg}_{(aq)}^{2+}+2{\rm Cl}_{(aq)}^-+4,5\ H_2O_{(l)}$$
2. Décrire précisément un protocole expérimental à mettre en œuvre pour préparer 100,0 mL de solution aqueuse S2 à partir de la solution aqueuse S1.
La solution S2 est obtenue par dilution d’un facteur cinq de la solution S1. Ainsi le volume V2 est 5 fois plus grand que V1.
Or on désire V2=100mL, on doit donc prendre V1=20mL
Protocole :
- Verser la solution mère dans un bécher
- Prélever à l’aide d’une pipette jaugée V1=20mL de la solution mère
- Introduire dans une fiole jaugée V2=100mL,
- Ajouter de l’eau distillée jusqu’au trait de jauge
- Homogénéiser la solution
Un dosage par titrage de la solution aqueuse S2 est réalisé par une solution aqueuse S titrante de nitrate d’argent, (Ag+(aq) ; NO3–(aq)), à la concentration CS = 5,0×10–2 mol·L–1. Pour cela, un volume de V2 = 10,0 mL de solution aqueuse S2 est prélevé et versé dans un bécher, auquel sont ajoutés environ 200 mL d’eau distillée. L’ensemble est alors titré par la solution aqueuse S et suivi par conductimétrie. La réaction support du titrage a pour équation :
Ag+ (aq) + Cℓ– (aq) → AgCℓ (s)
3. Les ions magnésium Mg2+ et nitrate NO3– sont des espèces spectatrices lors du titrage. Indiquer la signification de l’adjectif « spectatrice » donné à ces espèces.
Les espèces spectatrices ne réagissent pas lors de la réaction.
La conductivité σ de la solution contenue dans le bécher est mesurée après chaque ajout de solution aqueuse titrante S. Les résultats expérimentaux obtenus sont reproduits dans la représentation graphique ci-dessous (figure 2) :
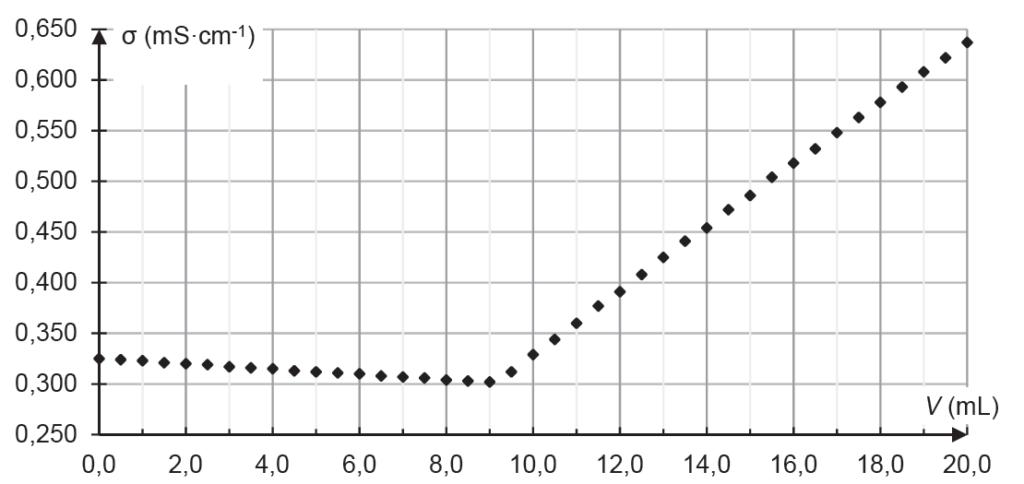
4. En utilisant les conductivités molaires ioniques, justifier l’allure de la courbe obtenue et déterminer la valeur du volume à l’équivalence du titrage.
Ag+ (aq) + Cl− (aq) → AgCl(s)
| Ions | Avant l’équivalence |
| Ag+ | 0 |
| Cl− | ↘ |
| NO3– | ↗ |
| Mg2+ | = |
Avant l’équivalence :
- les ions Ag+ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, la concentration des ions Ag+ est nulle.
- les ions Cl− sont consommés, la concentration des ions Cl− diminue.
- les ions NO3– sont ajoutés, ils ne réagissent pas, la concentration des ions augmente.
- les ions Mg2+ sont présents initialement, ils ne réagissent pas, la concentration des ions Mg2+ ne change pas.
Or , diminue donc avant l’équivalence.
| Ions | Après l’équivalence |
| Ag+ | ↗ |
| Cl− | 0 |
| NO3– | ↗ |
| Mg2+ | = |
Après l’équivalence :
- les ions Ag+ sont ajoutés et ne sont plus consommés, la concentration des ions Ag+ augmente.
- les ions Cl− n’existent plus, la concentration des ions Cl− est nulle.
- les ions NO3– sont ajoutés, ils ne réagissent pas, la concentration des ions augmente.
- les ions Mg2+ sont présents initialement, ils ne réagissent pas, la concentration des ions Mg2+ ne change pas.
La concentration des ions augmente, ainsi augmente donc après l’équivalence.
5. Calculer la concentration en ions chlorure Cℓ– dans la solution S1, puis montrer que la masse de chlorure de magnésium MgCℓ2, dans le sachet analysé, est de m(MgCℓ2) = 10,8 g.
A l’équivalence :
$$\frac{n_{{\rm Cl}^-}^i}{1}=\frac{n_{{\rm Ag}^+}^{eq}}{1}$$
$$\left[{\rm Cl}^-\right]_2 \times V_2=C_S \times V_{eq}$$
$$\left[{\rm Cl}^-\right]_2=\frac{C_S \times V_{eq}}{V_2}$$
$$\left[{\rm Cl}^-\right]_2=\frac{5,0.{10}^{-2} \times 9,0.{10}^{-3}}{10,0.{10}^{-3}}=4,5.{10}^{-2}mol.L^{-1}$$
Diluée 5 fois : $$\left[{\rm Cl}^-\right]_1=5\left[{\rm Cl}^-\right]_2$$
$$\left[{\rm Cl}^-\right]_1=5 \times 4,5.{10}^{-2}=0,225\ mol.L^{-1}$$
D’après la question 1 : $$\left[{\rm Cl}^-\right]_1=2c$$
$$c=\frac{\left[{\rm Cl}^-\right]_1}{2}=\frac{0,225\ }{2}=0,113\ mol.L^{-1}$$
$$m=n \times M$$
$$m=c \times V \times M$$
$$m=0,113\ \times 1,0 \times 95,3=10,7\ g$$
6. En déduire le degré d’hydratation du chlorure de magnésium étudié. Conclure.
$$m_{sachet}=m_{{\rm MgCl}_2}+m_{H_2O}$$
$$m_{H_2O}=m_{sachet}-m_{{\rm MgCl}_2}$$
$$m_{H_2O}=20,3-10,8=9,5\ g$$
$$n_{H_2O}=\frac{m_{H_2O}}{M_{H_2O}}=\frac{9,5\ }{2 \times 1,0+16,0}=0,53\ mol$$
$$n_{{\rm MgCl}_2}=\frac{m_{{\rm MgCl}_2}}{M_{{\rm MgCl}_2}}=\frac{10,7\ }{95,3}=0,11\ mol$$
$${\rm MgCl}_2,\ xH_20$$
| $1 mol de {\rm MgCl}_2 $ | $x\ moles\ \ de\ H_20$ |
| $0,11 mol de {\rm MgCl}_2$ | $0,53\ \ moles\ \ de\ H_20$ |
$$x=\frac{0,53 \times 1\ }{0,11\ }=4,8$$
Le degré est conforme à l’indication.
