Asie septembre 2025 Sujet 2
Exercice 3 – (4 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°25-PYCPE4
Sujet et corrigé
EXERCICE 3 – DOSAGE DU PHOSPHORE DANS UNE EAU DE PISCINE (4 POINTS)
La pollution d’une eau peut être due à différentes espèces chimiques. La pollution au phosphore est souvent sous-estimée mais peut être la cause d’une prolifération d’algues vertes, et réduire l’efficacité des produits de traitement, ce qui pose un problème, notamment dans les bassins de piscine.
Le phosphore existe sous diverses formes : PO43–, HPO42–, H2PO4– et H3PO4. Par souci de simplification, nous appellerons ces espèces « espèces phosphorées ».
L’objectif de cet exercice est d’effectuer un contrôle qualité de l’eau d’une piscine pour savoir s’il y a un risque de prolifération d’algues.
Données :
• couples acide-base des espèces phosphorées accompagnées de leur valeur de pKa :
H3PO4 (aq) / H2PO4– (aq) pKa1 = 2,1 ;
H2PO4– (aq) / HPO42–(aq) pKa2 ;
HPO42– (aq) / PO43– (aq) pKa3.
Le diagramme de distribution des couples acide-base des espèces phosphorées est représenté figure 1.
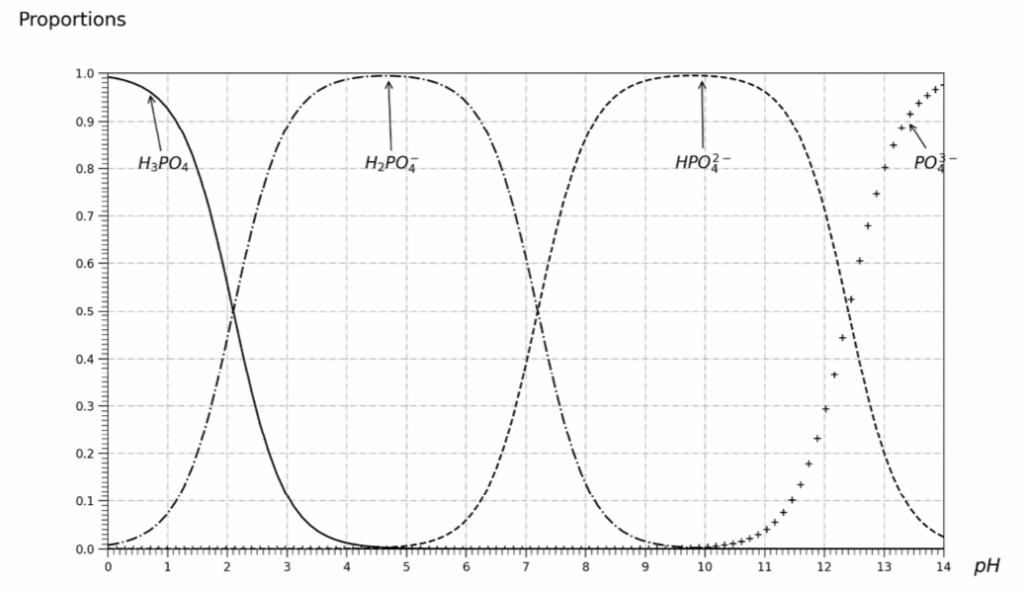
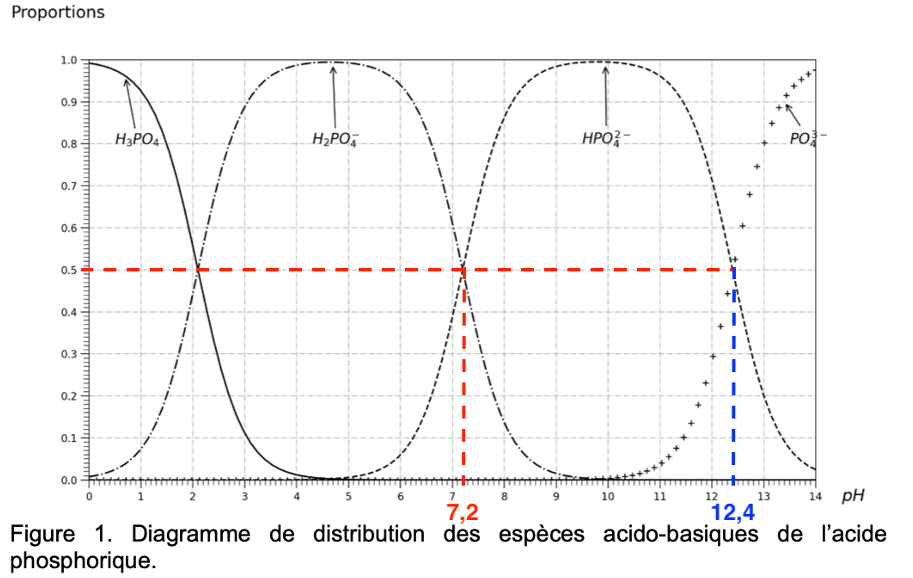
Figure 1. Diagramme de distribution des espèces acido-basiques de l’acide phosphorique.
Q1. À l’aide de la figure 1, déterminer la valeur du pKa2 du couple (H2PO4– (aq) / HPO42–(aq)) et la valeur du pKa3 du couple (HPO42– (aq) / PO43– ).
$pH={\rm pK}_{a2}+log\left(\frac{\left[{\rm HPO}4^{2-}\right]{eq}}{\left[{H_2PO}4^-\right]{eq}}\right)$
Lorsque $\left[{\rm HPO}4^{2-}\right]{eq}=\left[{H_2PO}4^-\right]{eq}$
$pH={\rm pK}{a2}+log\left(1\right)$
$pH={\rm pK}{a2}$
Graphiquement $\left[{\rm HPO}4^{2-}\right]{eq}=\left[{H_2PO}4^-\right]{eq}$ pour $pH=7,2$.
Ainsi, ${\rm pK}_{a2}=7,2$
$pH={\rm pK}_{a3}+log\left(\frac{\left[{\rm PO}4^{3-}\right]{eq}}{\left[{\rm HPO}4^{2-}\right]{eq}}\right)$
Lorsque $\left[{\rm PO}4^{3-}\right]{eq}=\left[{\rm HPO}4^{2-}\right]{eq}$
$pH={\rm pK}{a3}+log\left(1\right)$
$pH={\rm pK}{a3}$
Graphiquement $\left[{\rm PO}4^{3-}\right]{eq}=\left[{\rm HPO}4^{2-}\right]{eq}$ pour $pH=12,4$.
Ainsi, ${\rm pK}_{a3}=12,4$
Q2. Représenter le diagramme de prédominance de ces espèces phosphorées. En déduire la nature de l’espèce phosphorée majoritaire dans l’eau d’une piscine dont le pH vaut 7,0.
Diagramme de prédominance

Pour $pH=7,0$ ${H_2PO}_4^-$ est prédominant.
Ainsi, la nature de l’espèce phosphorée majoritaire dans l’eau d’une piscine dont le pH vaut 7,0 est ${H_2PO}_4^-$.
Les espèces phosphorées sont incolores. Dans l’objectif de réaliser un dosage spectrophotométrique, il est donc nécessaire d’ajouter à la solution un réactif spécifique qui permettra de former un composé coloré.
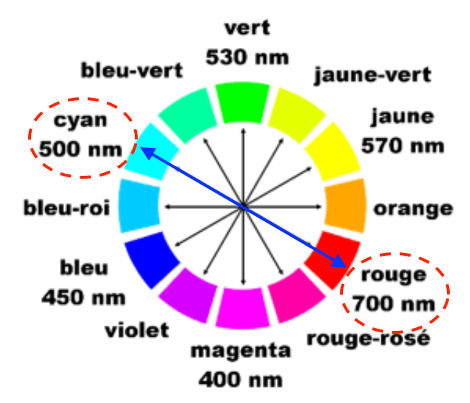
Le spectre d’absorbance du composé coloré ainsi que le cercle chromatique sont donnés en figure 2.
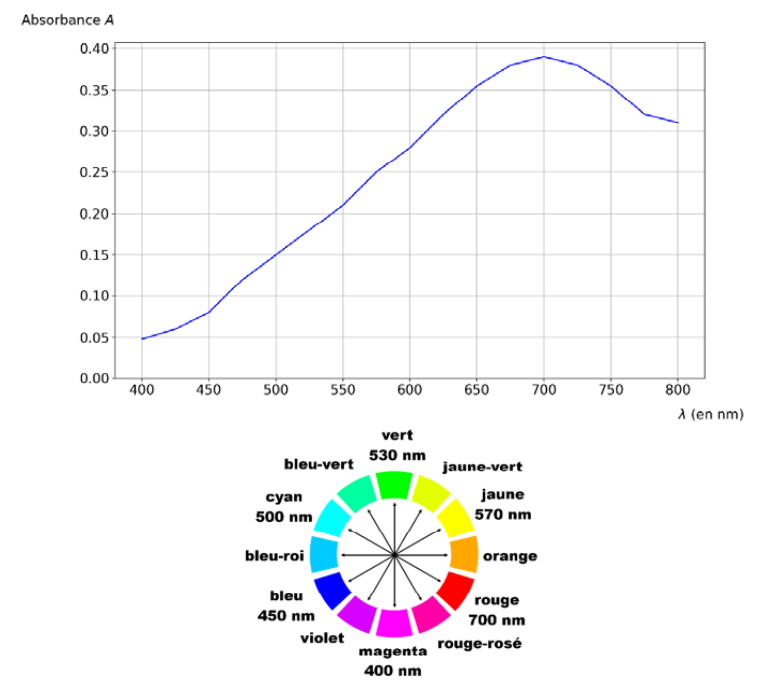
Figure 2. Spectre d’absorbance du composé coloré et cercle chromatique.
Q3. À l’aide de la figure 2 et en expliquant votre démarche, proposer une valeur de longueur d’onde λ à laquelle il serait judicieux de régler le spectrophotomètre. Préciser, en justifiant, la couleur du composé coloré formé après ajout du réactif.
La valeur de la longueur d’onde à laquelle il faut régler le spectrophotomètre pour réaliser les mesures d’absorbance est la valeur pour laquelle l’absorbance est maximale soit
$$\lambda_{max}=700\ {\rm nm}$$
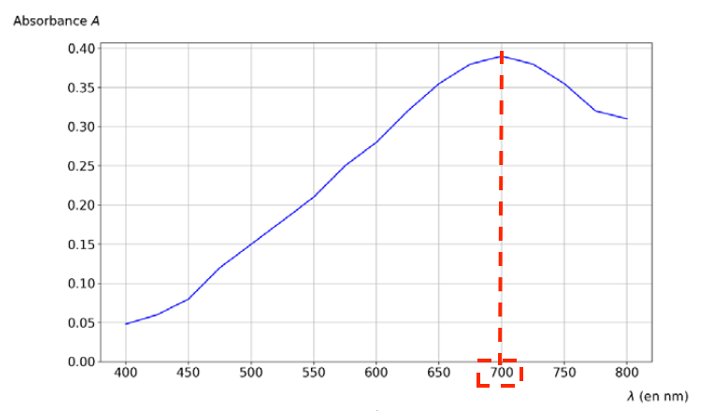
La couleur absorbée correspond à $\lambda_{max}=700\ {\rm nm}$ couleur rouge absorbée.
La couleur du composé coloré formé après ajout du réactif est la couleur complémentaire du rouge (couleur opposée sur la cercle chromatique) : le cyan.
Ainsi, la couleur du composé coloré formé après ajout du réactif est le cyan.
Dans l’objectif de préparer une gamme étalon, on cherche, dans un premier temps, à fabriquer une solution S0 de concentration en quantité de matière en espèce phosphorée C(S0) = 3,67×10 –3 mol·L–1.
Le solide utilisé pour la dissolution est le dihydrogénophosphate de potassium de formule brute KH2PO4. On considére alors que tout le solide se dissout et que la quantité de matière en espèce phosphorée dissoute est égale à la quantité de matière de solide introduite.
Donnée :
- masse molaire du dihydrogénophosphate de potassium solide : M(KH2PO4) = 136 g∙mol–1.
Q4. Montrer que la masse m qu’il faut prélever pour préparer la solution S0 dans une fiole jaugée de volume V = 200 mL est voisine de 100 mg.
$$n=\frac{m}{M}$$
$$\frac{m}{M}=n$$
$$m=n\times M$$
Or
$$c=\frac{n}{V}$$
$$\frac{n}{V}=c$$
$$n=c\times V$$
D’où
$$m=c\times V\times M$$
$$m=3,67\times 10^{-3}\ \ \times 200,0\times 10^{-3}\times 136$$
$$m=9,98\times 10^{-2}\ g$$
$$m=99,8\times 10^{-3}\ g$$
$$m=99,8\ mg$$
Ainsi, la masse m qu’il faut prélever pour préparer la solution S0 dans une fiole jaugée de volume V = 200 mL est voisine de 100 mg.
Les concentrations en masse en espèces phosphorées présentes dans l’eau de piscine sont relativement faibles (de l’ordre de 0,05 à 1,00 mg par litre de solution). C’est pourquoi il est nécessaire de diluer au préalable cette solution S0 cent fois pour obtenir une solution notée S.
Q5. Écrire en le détaillant, le protocole de la préparation de la solution S à partir de la solution S0. Préciser la verrerie utilisée ainsi que son volume.
D’après l’énoncé : « il est nécessaire de diluer au préalable cette solution S0 cent fois pour obtenir une solution notée S. »
$$F=\frac{V}{V_0}$$
$$\frac{V}{V_0}=F$$
$$V=F\times V_0$$
$$V=100\times V_0$$
Le volume V de la solution fille (volume de la fiole jaugée), doit être 100 plus grand que le volume V0 de la solution mère (volume de la pipette jaugée).
On choisit (plusieurs réponses possibles) :
- une pipette jaugée V0=5,00 mL
- une fiole jaugée V=500,0 mL
Protocole expérimental permettant de préparer la solution S :
- Prélever, à l’aide d’une pipette jaugée de 5,00 mL de la solution mère.
- Introduire le prélèvement dans une fiole jaugée de 500,0 mL.
- Ajouter au ¾ de l’eau distillée et homogénéiser.
- Ajuster avec de l’eau distillée jusqu’au trait de jauge.
- Homogénéiser.
Une gamme étalon est enfin effectuée à partir de la solution S en suivant le protocole suivant :
- on prélève un volume de solution S selon les conditions résumées dans le tableau ci-dessous et on l’insère dans une fiole jaugée de 25,0 mL ;
- un volume de 5,00 mL de réactif spécifique permettant la formation du complexe coloré est ajouté dans chaque fiole ;
- chaque solution est complétée avec de l’eau distillée jusqu’au trait de jauge de la fiole jaugée qui est ensuite bouchée et agitée ;
- l’absorbance de chaque solution de la gamme étalon est alors mesurée.
| Solution de volume total 25 mL | SF0 | SF1 | SF2 | SF3 | SF4 |
| Volume de solution S (en mL) | 0 | 2,50 | 5,00 | 7,50 | 10,0 |
| Concentration en masse C en espèces phosphorées en mg·L–1 | 0 | 0,50 | 1,00 | 1,50 | 2,00 |
| Absorbance mesurée | 0,000 | 0,080 | 0,162 | 0,231 | 0,311 |
Tableau donnant les concentrations en masse des solutions filles élaborées. La courbe d’étalonnage correspondant à ces solutions filles a été réalisée :
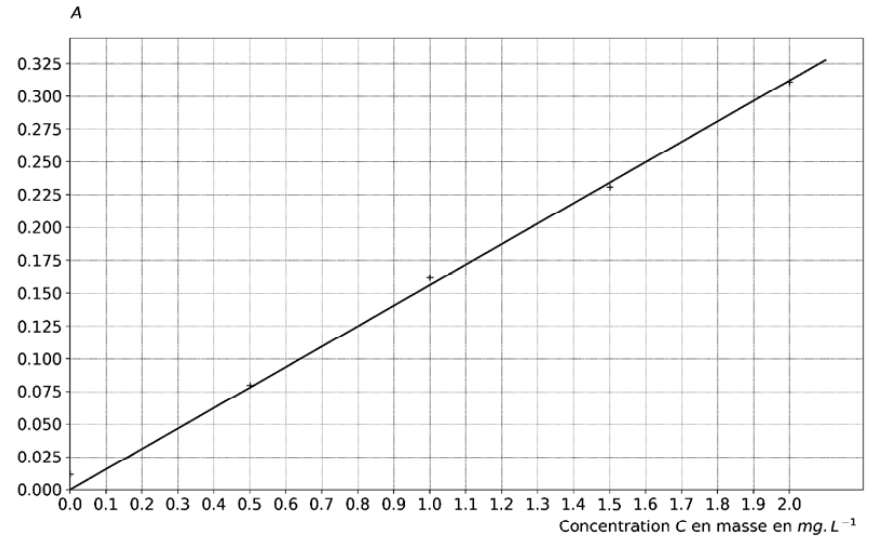
Figure 3. Graphique représentant l’absorbance des solutions étalon en fonction de leur concentration en masse C en espèces phosphorées.
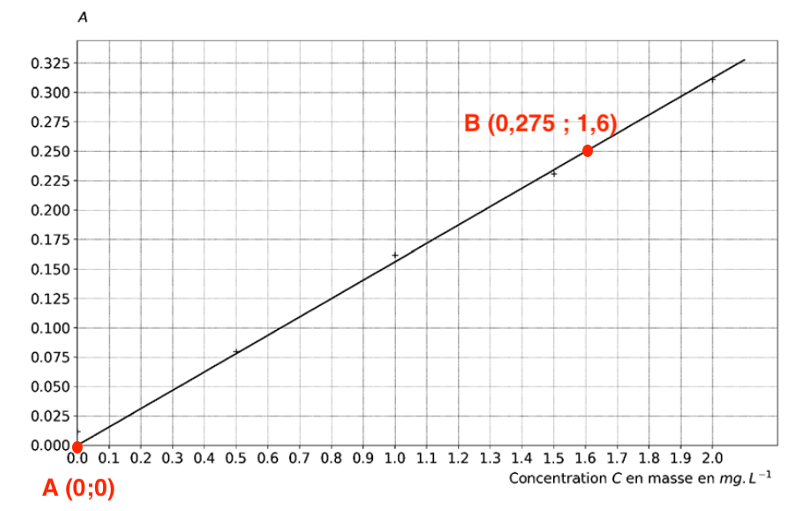
Q6. Justifier que l’absorbance peut être modélisée par la relation A = k·C et vérifier que le coefficient k a pour valeur 0,156 L∙mg−1 à l’aide d’une méthode de votre choix.
A en fonction de C est une droite passant par l’origine :
A et C sont proportionnels : $A=kC$.
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{0,275-0}{1,6-0}$$
$$k=0,156\ {\rm L.mg^{-1}}$$
Avant d’analyser l’échantillon d’eau de piscine, il est nécessaire de le filtrer sur filtre Büchner. Le filtrat est ainsi récupéré.
On récupère après la filtration sur filtre Büchner, Vfiltrat = 5,00 mL du filtrat de l’eau de la piscine qui est placé dans une fiole jaugée de 25,0 mL, auquel on ajoute Vréactif = 5,00 mL de réactif spécifique afin d’obtenir le complexe coloré. On complète avec de l’eau distillée jusqu’au trait de jauge et on agite.
L’absorbance de la solution filtrée et colorée est ensuite mesurée à la même longueur d’onde que précédemment. L’absorbance mesurée vaut Aeau = 0,075.
Données :
| Concentration en masse en espèces phosphorées (en mg·L–1) | Qualité de l’eau |
| 0,05 – 0,2 | Bonne |
| 0,2 – 0,5 | Passable |
| 0,5 – 1,0 | Mauvaise |
| Supérieure à 1,0 | Très mauvaise |
Tableau donnant la qualité de l’eau en fonction de la concentration en masse en espèces phosphorées
Source : SAGE Mayenne – Janvier 2013 Source : BD Carthage®©IGN MATE 2001 Agence de l’eau – CG
Q7. À partir des données et des résultats expérimentaux, donner la qualité de l’eau de piscine étudiée.
L’absorbance mesurée vaut $A_{\rm eau}=0,075$
D’après Q6 : $A=kC$ avec $k=0,156\ {\rm L.mg^{-1}}$
$$A=0,156\times C$$
$$0,156\times C=A$$
$$C=\frac{A}{0,156}$$
$$C=\frac{0,075}{0,156}$$
$$C=0,481\ {\rm mg.L^{-1}}$$
Or $V_{\rm filtrat}=5,00\ {\rm mL}$ placé dans une fiole de $25,0\ {\rm mL}$.
On dilue donc 5 fois :
$F=\frac{V_f}{V_{\rm filtrat}}=\frac{25,0}{5,00}=5$
Ainsi, la solution mesurée est 5 fois moins concentrée que l’eau de piscine.
$$F=\frac{C_p}{C_d}$$
$$\frac{C_p}{C_d}=F$$
$$C_p=F\times C_d$$
$$C_p=5\times 0,481$$
$$C_p=2,41\ {\rm mg.L^{-1}}$$
Concentration en masse > 1,0 mg·L⁻¹ : la qualité de l’eau de piscine est très mauvaise.

