Métropole 2025 Sujet 2
Exercice 2 – (4 points) – Durée 0h42 – Calculatrice autorisée
Sujet n°25-PYCJ2ME1
Sujet et corrigé
Exercice 2 – Eau de Quinton (4 points)
René Quinton, biologiste français, a découvert et mis au point le sérum qui porte son nom : l’eau de Quinton. Issue d’un prélèvement d’eau de mer, celle-ci est ensuite filtrée pour en éliminer les impuretés. Elle est actuellement commercialisée, notamment sous forme d’ampoules pour, par exemple, nettoyer le nez ou les yeux.
L’objectif de cet exercice est de déterminer la teneur en ions chlorure d’une eau de Quinton commerciale provenant d’une mer bretonne, à l’aide d’un titrage suivi par conductimétrie.
Données :
- conductivités molaires ioniques à 25 °C :
| ion | Cℓ– | Ag+ | NO3− | Na+ |
| λ (S∙m2∙mol−1) | 7,63×10−3 | 6,19×10−3 | 7,14×10−3 | 5,01×10−3 |
- masse molaire atomique de l’élément chlore : M(Cℓ) = 35,5 g·mol–1 ;
- concentration moyenne en masse en ions chlorure d’une eau de mer bretonne : 19,4 g·L–1 ;
- la concentration en ions chlorure dans le sang est comprise entre 100 et 110 mmol∙L–1 ;
- pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\left|\frac{x-x_\text{ref}}{u(x)}\right|$ avec x la valeur mesurée, xref la valeur de référence et u(x) l’incertitude-type associée à la valeur mesurée x.
Dans le contexte de cet exercice, on peut qualifier une eau de Quinton d’isotonique si sa concentration en ions chlorure est dans l’intervalle des valeurs de celles du sang, d’hypertonique si elle est supérieure à 110 mmol∙L–1 et d’hypotonique si elle est inférieure à 100 mmol∙L–1.
1. Préparation de l’eau de Quinton isotonique
Une eau de Quinton isotonique est préparée en diluant 5 fois l’eau de Quinton commerciale hypertonique étudiée.
Q1. Proposer un protocole permettant de préparer 100,0 mL d’eau de Quinton isotonique à partir d’eau de Quinton commerciale. Nommer, en précisant les volumes, la verrerie utilisée.
D’après l’énoncé : « l’eau de Quinton isotonique est préparée en diluant 5 fois l’eau de Quinton commerciale hypertonique étudiée. »
$$F=\frac{V_1}{V_0}$$
$$F\times V_0=V_1$$
$$V_0=\frac{V_1}{F}$$
$$V_0=\frac{100,0}{5}$$
$$V_0=20,0\ mL$$
On choisit :
- une fiole jaugée V1=100,0 mL
- une pipette jaugée V0=20,0 mL
Protocole expérimental permettant de préparer la solution S :
- Prélever, à l’aide d’une pipette jaugée de 20,0 mL de la solution mère.
- Introduire le prélèvement dans une fiole jaugée de 100,0 mL.
- Ajouter au ¾ de l’eau distillée et homogénéiser.
- Ajuster avec de l’eau distillée jusqu’au trait de jauge.
- Homogénéiser.
Q2. Vérifier le caractère isotonique de la solution ainsi préparée.
D’après le sujet : «… eau de Quiton commerciale provenant d’une mer bretonne »
$$c_m=c\times M$$
$$c\times M=c_m$$
$$c=\frac{c_m}{M}$$
$$c=\frac{19,4}{35,5}$$
$$c=0,546\ mol.L^{-1}$$
D’après l’énoncé : « l’eau de Quinton isotonique est préparée en diluant 5 fois l’eau de Quinton commerciale hypertonique étudiée. »
$$F=\frac{c_0}{c_1}$$
$$Ftimes _1=c_0$$
$$c_1=\frac{c_0}{F}$$
$$c_1=\frac{0,546}{5}$$
$$c_1=0,109\ mol.L^{-1}$$
$$c_1=109\ mmol.L^{-1}$$
D’après le sujet :
- Dans le contexte de cet exercice, on peut qualifier une eau de Quinton d’isotonique si sa concentration en ions chlorure est dans l’intervalle des valeurs de celles du sang
- la concentration en ions chlorure dans le sang est comprise entre 100 et 110 mmol∙L–1 ;
La concentration en ion chlorure est comprise entre 100 et 110 mol.L-1 (concentration en ions dans le sang). Ainsi, la solution préparée est isotonique.
2. Analyse d’une eau de Quinton hypertonique
On assimile l’eau de Quinton hypertonique étudiée à une solution aqueuse de chlorure de sodium (Na+(aq) ; Cℓ–(aq)). Afin d’en déterminer la concentration en ions chlorure, on réalise un titrage suivi par conductimétrie.
À l’aide d’une pipette jaugée, on prélève un volume V1 = 10,0 mL d’eau de Quinton hypertonique que l’on introduit dans un bécher, dans lequel on ajoute 200 mL d’eau distillée.
On dose la solution obtenue par une solution titrante de nitrate d’argent (Ag+(aq) ; NO3−(aq)) de concentration C2 = 3,00×10–1 mol·L–1. Les ions argent forment avec les ions chlorure un précipité de chlorure d’argent AgCℓ(s). Cette réaction de précipitation peut être considérée comme totale.
Q3. Écrire l’équation de la réaction modélisant la transformation mise en jeu au cours du titrage.
Les ions argent forment avec les ions chlorure un précipité de chlorure d’argent AgCℓ(s) :
$${\rm Ag}{(aq)}^++{\rm Cl}{(aq)}^-\rightarrow{\rm AgCl}{(s)}$$
On utilise le langage de programmation Python pour simuler et représenter l’évolution des concentrations des espèces qui participent à la conductivité de la solution titrée en fonction du volume de solution titrante versé. On néglige la dilution liée à l’ajout de la solution titrante.
Dans ce programme, on utilise les notations suivantes :
- C_1 : concentration de la solution titrée exprimée en mol·L–1 ;
- V_1 : volume de solution titrée exprimé en L ;
- C_2 : concentration de la solution titrante exprimée en mol·L–1 ;
- V_2 : volume de solution titrante versé exprimé en L.
On fournit sur la figure 1 un extrait du programme et sur la figure 2 le résultat de la simulation obtenu.
| 8 # Déclaration des variables 9 10 c_A = [] # Concentration de l’espèce A 11 c_B = [] # Concentration de l’espèce B 12 c_C = [] # Concentration de l’espèce C 13 c_D = [] # Concentration de l’espèce D 14 15 V_E = # Expression du volume équivalent exprimé en L |
Figure 1. Extrait du programme
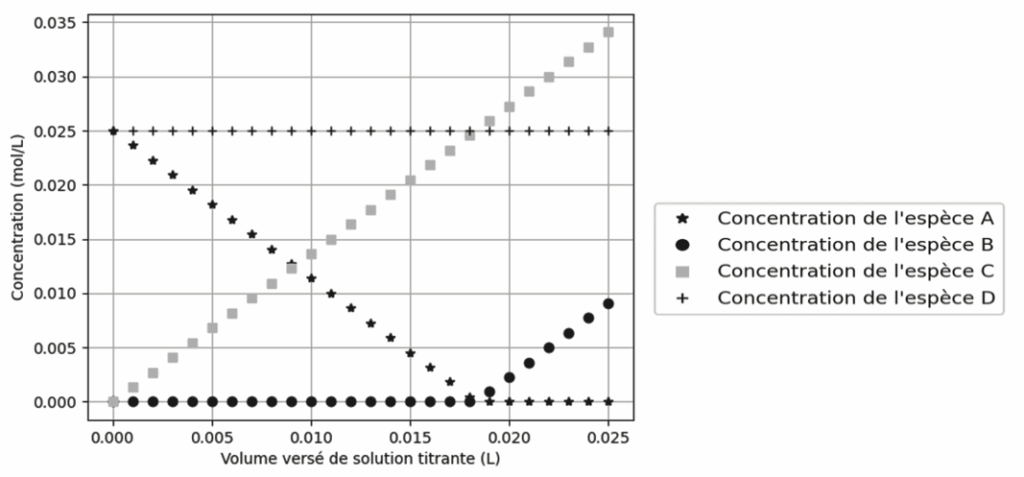
Figure 2. Évolution des concentrations en fonction du volume de solution titrante versé
Q4. Identifier, en justifiant, les espèces A, B, C et D parmi Na+, Cℓ–, NO3− et Ag+.
Avant l’équivalence :
les ions ${\rm Ag}^+$ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, la concentration des ions ${\rm Ag}^+$ est nulle.
les ions ${\rm NO}_3^-$ sont ajoutés, ils ne réagissent pas, la concentration des ions ${\rm NO}_3^-$ augmente.
les ions ${\rm Cl}^-$ sont consommés, la concentration des ions ${\rm Cl}^-$ diminue.
les ions ${\rm Na}^+$ sont spectateurs et sont présents initialement, la concentration des ions ${\rm Na}^+$ est constante.
Après l’équivalence :
les ions Ag+ sont ajoutés et ne sont plus consommés, la concentration des ions Ag+ augmente.
les ions NO3− sont ajoutés, ils ne réagissent pas, la concentration des ions NO3− augmente.
les ions Cℓ– n’existent plus, la concentration des ions Cℓ– est nulle.
les ions Na+ sont spectateurs et sont présents initialement, la concentration des ions Na+ est constante.
| Ions | Avant l’équivalence | Après l’équivalence | |
| Ag+ | 0 | ↗ | nB |
| NO3− | ↗ | ↗ | nC |
| Cℓ– | ↘ | 0 | nA |
| Na+ | = | = | nD |
A : ${\rm Cl}^-$
B : ${\rm Ag}^+$
C : ${\rm NO}_3^-$
D : ${\rm Na}^+$
Q5. Donner l’expression de la ligne 15 du programme Python permettant de calculer la valeur du volume à l’équivalence, noté V_E, en fonction de C_1, C_2 et V_1.
$${\rm Ag}{(aq)}^++{\rm Cl}{(aq)}^-\rightarrow{\rm AgCl}_{(s)}$$
A l’équivalence :
$$\frac{n_{{\rm Cl}^-}^i}{1}=\frac{n_{{\rm Ag}^+}^{eq}}{1}$$
$$c_1\times V_1=c_2\times V_{eq}$$
$$c_2\times V_{eq}=c_1\times V_1$$
$$V_{eq}=\frac{c_1\times V_1}{c_2}$$
Expression de la ligne 15 du programme Python :
V_E=C_1*V_1/C_2
On a reporté sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE l’évolution de la conductivité σ en fonction du volume V2 de solution de nitrate d’argent versé.
Q6. En utilisant les résultats de la simulation de la figure 2, expliquer l’évolution de la conductivité mesurée au cours du dosage
Avant l’équivalence :
les ions Ag+ sont ajoutés et consommés immédiatement, ils constituent le réactif limitant, la concentration des ions Ag+ est nulle.
les ions NO3− sont ajoutés, ils ne réagissent pas, la concentration des ions NO3− augmente.
les ions Cℓ– sont consommés, la concentration des ions Cℓ– diminue.
les ions Na+ sont spectateurs et sont présents initialement, la concentration des ions Na+ est constante.
Donc les ions Cℓ– sont remplacés par des ions NO3−
Or $\lambda{{\rm Cl}^-}>\lambda_{{\rm NO}_3^-\ }$ ainsi $\mathbf{\sigma}$ diminue avant l’équivalence.
| Ions | Avant l’équivalence |
| Ag+ | 0 |
| NO3− | ↗ |
| Cℓ– | ↘ |
| Na+ | = |
Après l’équivalence :
les ions Ag+ sont ajoutés et ne sont plus consommés, la concentration des ions Ag+ augmente.
les ions NO3− sont ajoutés, ils ne réagissent pas, la concentration des ions NO3− augmente.
les ions Cℓ–n’existent plus, la concentration des ions Cℓ– est nulle.
les ions Na+ sont spectateurs et sont présents initialement, la concentration des ions Na+ est constante.
La concentration des ions augmente, ainsi $\mathbf{\sigma}$ augmente après l’équivalence.
| Ions | Après l’équivalence |
| Ag+ | ↗ |
| NO3− | ↗ |
| Cℓ– | 0 |
| Na+ | = |
Q7. Exploiter les résultats expérimentaux pour déterminer la concentration en masse CQuinton des ions chlorure dans l’eau de Quinton.
$${\rm Ag}{(aq)}^++{\rm Cl}{(aq)}^-\rightarrow{\rm AgCl}_{(s)}$$
A l’équivalence :
$$\frac{n_{{\rm Cl}^-}^i}{1}=\frac{n_{{\rm Ag}^+}^{eq}}{1}$$
$$c_1\times V_1=c_2\times V_{eq}$$
$$c_1=\frac{c_2\times V_{eq}}{V_1}$$
On détermine graphiquement $$V_{eq}$$ à l’intersection des deux droites : $$V_{eq}=18,5\ mL$$
$$c_1=\frac{3,00{\times 10}^{-1}\times 18,5{\times 10}^{-3}}{10,0{\times 10}^{-3}}$$
$$c_1=0\ ,56\ mol{.L}^{-1}$$
Calculons la concentration massique $C_{Quinton}$ :
$$C_{Quinton}=c_1\times M$$
$$C_{Quinton}=0,56\times 35,5$$
$$C_{Quinton}=20\ g{.L}^{-1}$$
$$C_{Quinton}=20\ g{.L}^{-1}$$
L’incertitude-type u(CQuinton) associée à la valeur de la concentration en masse trouvée précédemment est, dans cette situation :
$$ u(C_\text{Quinton})=C_\text{Quinton}\times\sqrt{ \left(\frac{u(V_1)}{V_1}\right)^2 + \left(\frac{u(V_E)}{V_E}\right)^2 + \left(\frac{u(C_2)}{C_2}\right)^2 } $$
avec u(VE) = 0,5 mL, u(V1) = 0,02 mL et u(C2) = 2×10–3 mol·L–1.
Q8. Vérifier si la concentration trouvée est en accord avec la concentration en ions chlorure de l’eau de mer bretonne.
Calculons l’incertitude $u(C_{Quinton})$ :
$$u\left(C_{Quinton}\right)=C_{Quinton}\times \sqrt{\left(\frac{u\left(V_1\right)}{V_1}\right)^2+\left(\frac{u\left(V_E\right)}{V_E}\right)^2+\left(\frac{u\left(C_2\right)}{C_2}\right)^2}$$
$$u\left(C_{Quinton}\right)=20\times \sqrt{\left(\frac{0,02}{10,0}\right)^2+\left(\frac{0,5}{18,5}\right)^2+\left(\frac{2\times {10}^{-3}}{3,00{\times 10}^{-1}}\right)^2}$$
$$u\left(C_{Quinton}\right)=0,6\ g.L^{-1}$$
Pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient :
$$\frac{\left|x-x_{ref}\right|}{u\left(x\right)}$$ $$\frac{\left|C_{Quinton}-C_{m,mer}\right|}{u(C_{Quinton})}=\frac{\left|20-19,4\right|}{0,6}$$
$$\frac{\left|C_{Quinton}-C_{m,mer}\right|}{u(C_{Quinton})}=1<2$$
Ainsi, la concentration trouvée est en accord avec la concentration en ions chlorure de l’eau de mer bretonne.
ANNEXE À RENDRE AVEC LA COPIE
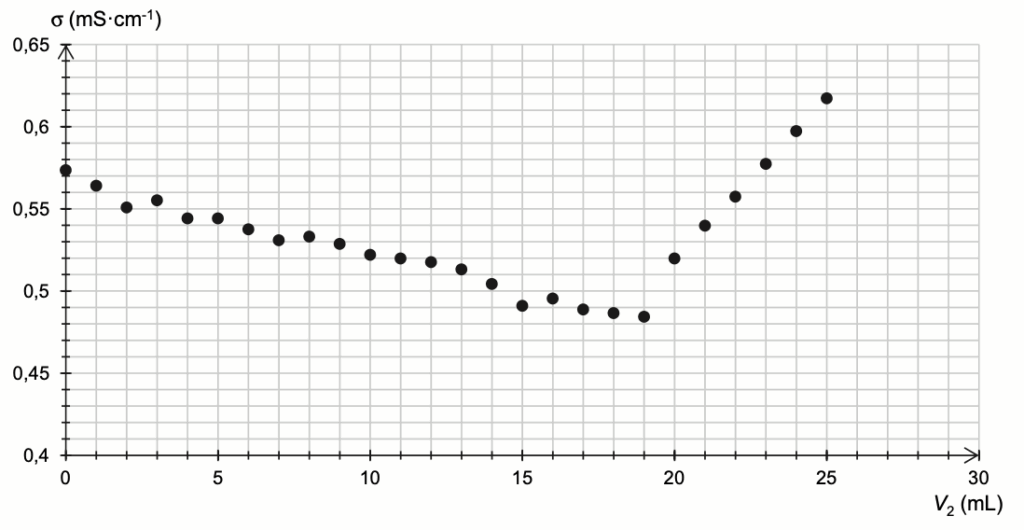
Figure A1. Évolution de la conductivité σ au cours du dosage en fonction du volume de solution de nitrate d’argent versé
