Métropole Septembre 2022 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ2ME3
Sujet et corrigé
Mots-clés : spectrophotométrie, dosage par étalonnage
On étudie une boisson verte à base de banane et de fruits tropicaux dont la recette est d’inspiration indonésienne. Elle est composée d’extraits de fruits, d’eau, d’éthanol, de sucre et de colorants alimentaires responsables de sa couleur vert vif.
L’objectif de cet exercice est d’identifier la nature des colorants présents dans cette boisson et de s’interroger sur les risques éventuels pour la santé de l’un d’entre eux.
Données :
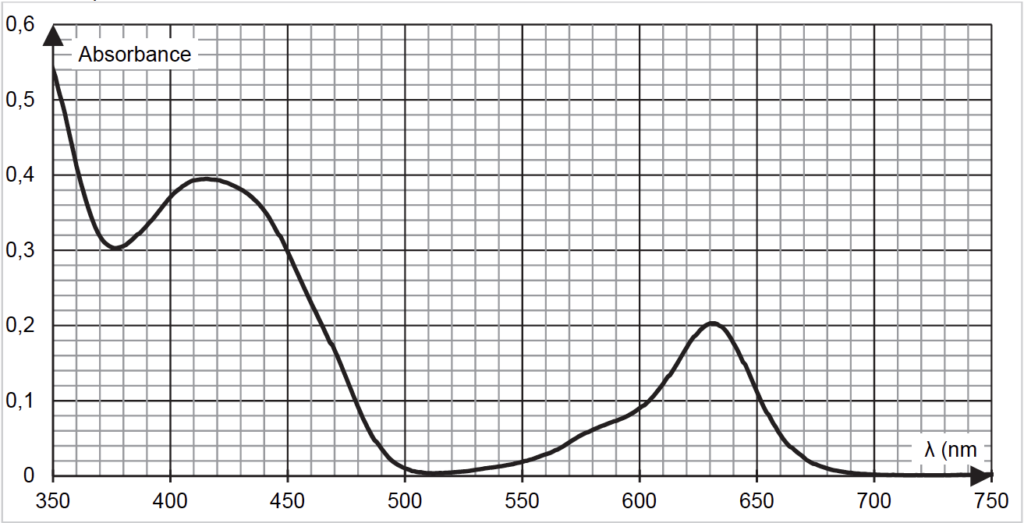
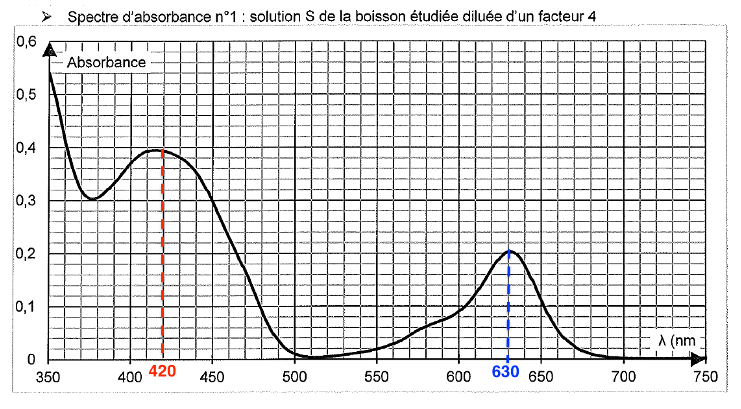
- Spectre d’absorbance n°1 : solution S de la boisson étudiée diluée d’un facteur 4
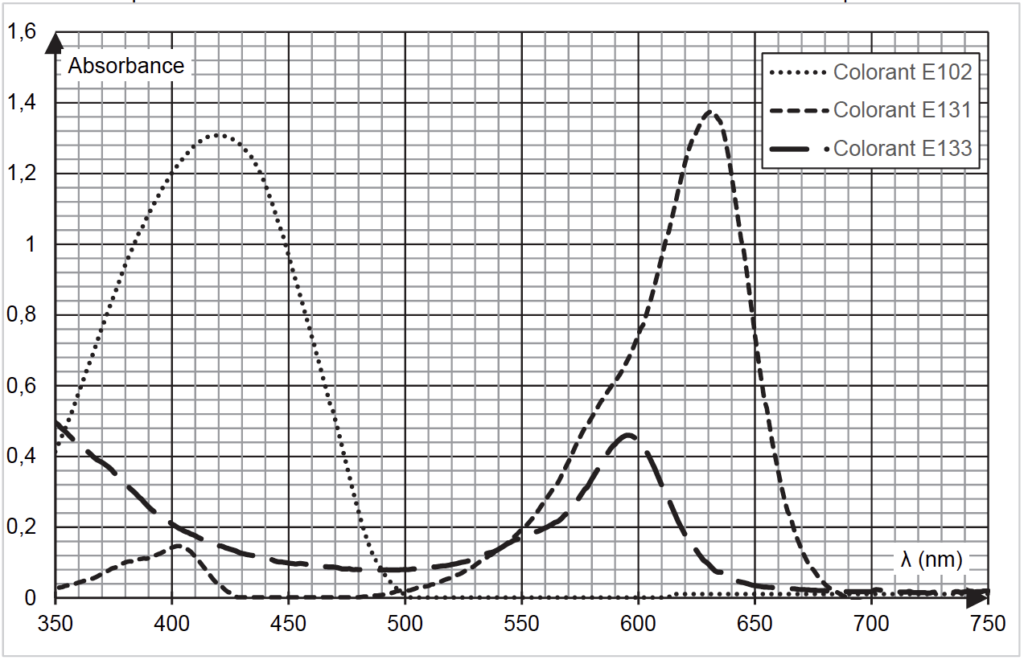
- Spectres d’absorbance n°2 : différents colorants alimentaires en solution aqueuse
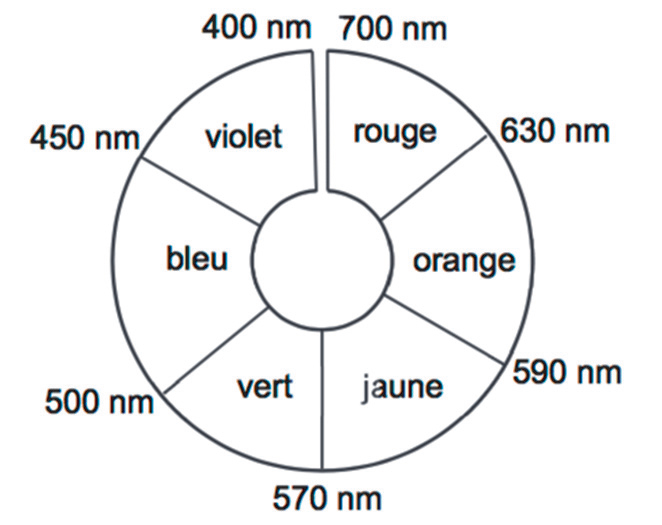
- Cercle chromatique :
- masse molaire du colorant E102 : M = 534 g·mol–1 ;
- volume de la boisson étudiée contenu dans un verre de cocktail : V = 3,0 cL ;
- concentration en masse de sucre dans la boisson étudiée : 367 g·L–1 ;
- masse d’un morceau de sucre : 5,0 g.
Q1. Déterminer le nombre de morceaux de sucre équivalent à la quantité de sucre apportée par la boisson étudiée lorsqu’on boit un verre de cocktail. Commenter.
Calculons la masse de sucre contenue dans un verre de boisson :
$c_m=\frac{m}{V}$
$\frac{m}{V}=c_m$
$m=c_m \times V$
$m=367 \times 3,0{.10}^{-2}$
$m=11\ g$
Déterminons le nombre de carreaux de sucre correspondant :
| 1 carreau | 5,0 g |
| N carreaux | 11 g |
$N=\frac{11 \times 1}{5,0}$
$N=2,2$
Il y a l’équivalent de 2,2 carreaux de sucre dans un verre de cocktail.
La couleur verte de la boisson étudiée est obtenue par le mélange de deux colorants alimentaires. On cherche à les identifier parmi les trois colorants analysés dans le spectre d’absorbance n°2.
Q2. Donner, en justifiant, la couleur en solution aqueuse de chacun des colorants alimentaires E102, E131, et E133.
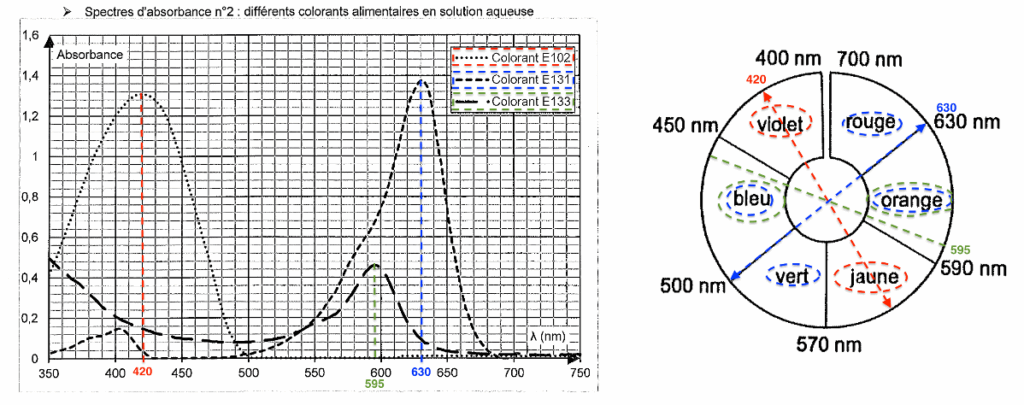
| Colorant | λmax | Couleur absorbée | Couleur du colorant (couleur complémentaire) |
| E102 | 420 nm | Violet | Jaune |
| E131 | 630 nm | Rouge-orange | Bleu-vert |
| E133 | 595 nm | Orange | Bleu |
Q3. Déterminer, en justifiant, les deux colorants majoritairement présents dans la boisson étudiée.
Les deux maximums présents sur le spectre d’absorbance de la solution S sont $\lambda_{max}=420\ \text{nm}$ (présence de E102) et $\lambda_{max}=630\ \text{nm}$ (présence de E131).
Les deux colorants majoritairement présents dans la solution sont le E102 et le E131.
La dose journalière admissible (DJA) d’un colorant est la masse maximale de colorant qu’une personne peut consommer par jour sans risque pour sa santé. Elle est habituellement exprimée en mg de substance par kg de poids corporel et par jour. Pour le colorant E102, elle est de 7,5 mg par kilogramme de masse corporelle et par jour.
Pour déterminer la concentration de ce colorant dans la boisson étudiée, on réalise une gamme de solutions étalons de concentrations différentes à partir d’une solution-mère S0 de colorant E102. On enregistre ensuite les spectres d’absorbance correspondants (figure 1).
Enfin, pour doser le colorant E102 dans la boisson étudiée, les spectres obtenus sont exploités à la longueur d’onde λ = 450 nm. On note Ci, avec i allant de 1 à 5, la concentration en colorant E102 de la solution Si.
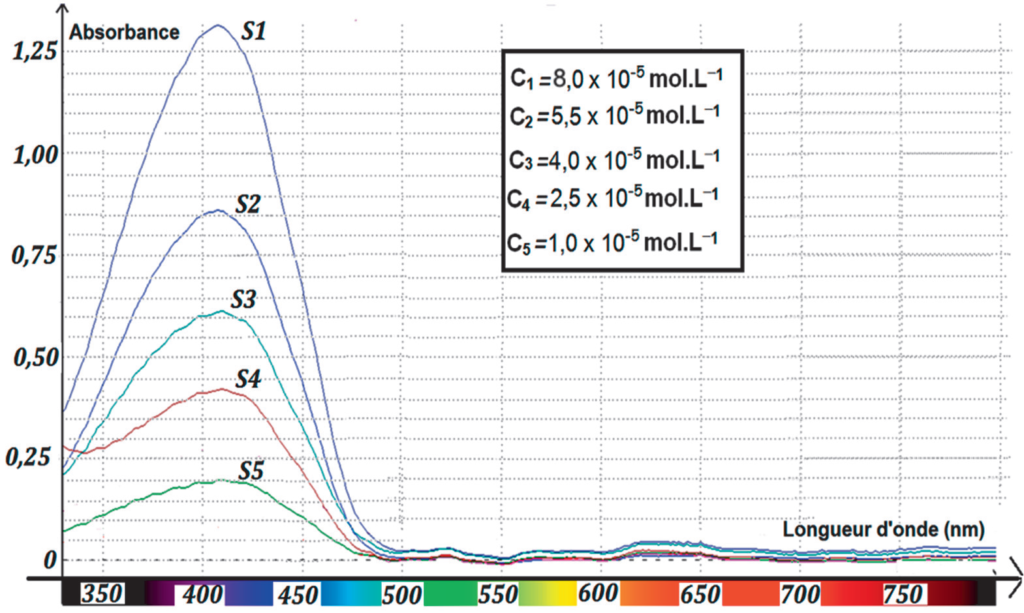
Figure 1. Spectres d’absorbance de 5 solutions de concentrations différentes en colorant E102.
Q4. À l’aide des spectres d’absorbance nos 1 et 2 fournis dans les données, expliquer le choix de la longueur d’onde λ = 450 nm plutôt que λ’ = 420 nm pour réaliser le dosage du colorant E102 dans la boisson étudiée.
Pour le E102, $\lambda_{max}=420\ \text{nm}$. Cependant, le E102 se trouve dans un mélange contenant aussi du E131. Pour $\lambda=420\ \text{nm}$, l’absorbance du E131 n’est pas nulle.
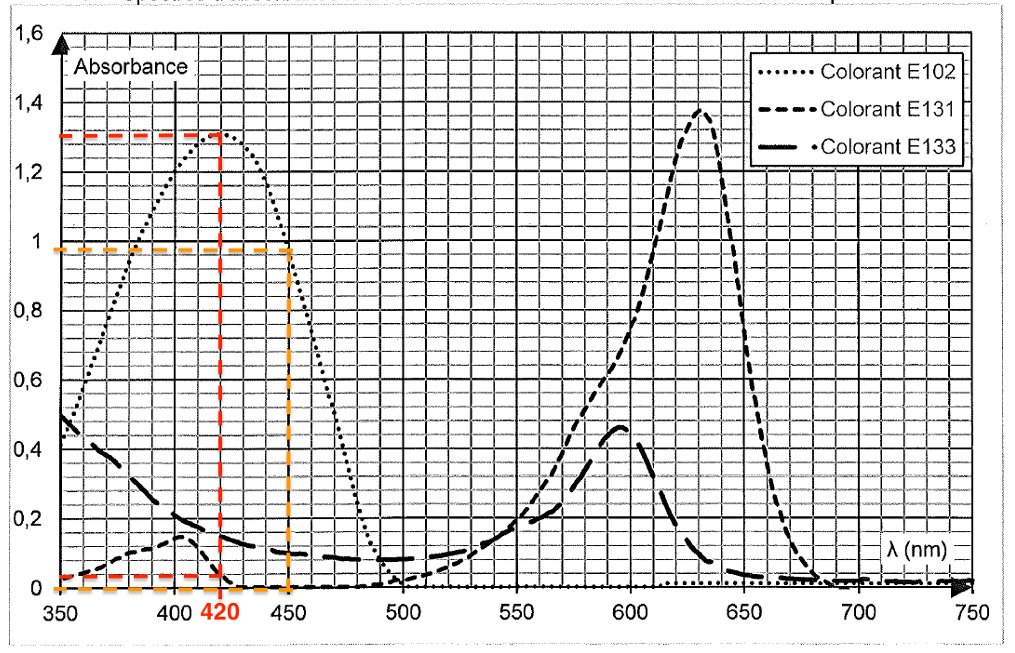
Or nous souhaitons doser le E102. Pour $\lambda=450\ \text{nm}$, l’absorbance du E131 est nulle. Ainsi, en choisissant $\lambda=450\ \text{nm}$, seul le E102 absorbe et est donc dosé.
On rappelle que le spectre d’absorbance n°1 est celui de la solution S de la boisson étudiée obtenue après dilution d’un facteur 4 de la solution commerciale.
Q5. Proposer un ensemble de verrerie permettant de préparer la solution S de la boisson étudiée diluée à partir de la solution commerciale.
Nous souhaitons faire une dilution de facteur $4$ :
$F=\frac{V_f}{V_m}=4$
$V_f=4 \times V_m$
Le volume fille est 4 fois plus grand que le volume mère.
On prend une pipette jaugée de $25\ \text{mL}$ (solution mère) et une fiole jaugée de $100\ \text{mL}$ (solution fille).
Q6. En explicitant la démarche suivie, montrer que, pour la longueur d’onde choisie de 450 nm, la loi de Beer- Lambert est vérifiée pour le colorant E102.
À l’aide de la figure 1, relevons les absorbances des solutions étalons pour $\lambda=450\ \text{nm}$ :
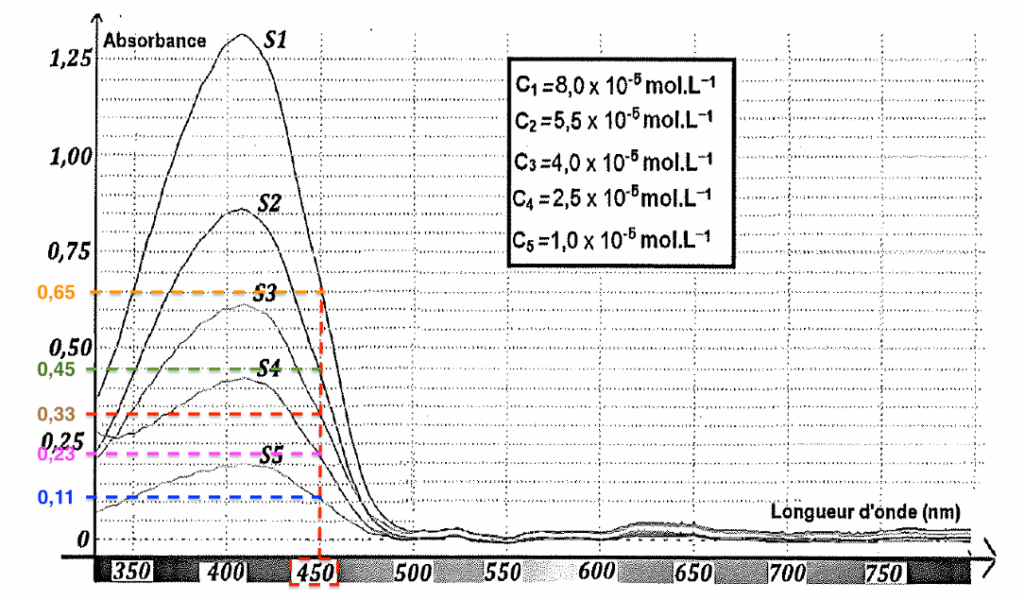
| Solution | 5 | 4 | 3 | 2 | 1 |
| Concentration (10-5 mol.L-1) | 1 | 2,5 | 4 | 5,5 | 8 |
| Absorbance | 0,11 | 0,23 | 0,33 | 0,45 | 0,65 |
Traçons A=f(c)
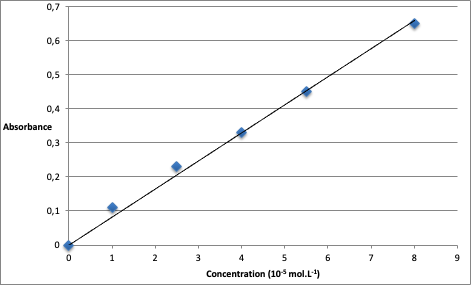
Graphiquement, c’est une droite passant par l’origine : la loi de Beer-Lambert est vérifiée.
Trouvons le coefficient directeur $k$ :
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{0,65-0}{8,0 \times 10^{-5}-0}$
$k=8,1 \times 10^{3}\ \text{L.mol}^{-1}$
$A=8,1 \times 10^{3}\ C$
Q7. Déterminer la masse de colorant E102 contenue dans un verre de cocktail. Commenter eu égard à la valeur de la DJA.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
D’après le spectre d’absorbance (solution S diluée par 4) à $\lambda=450\ \text{nm}$,
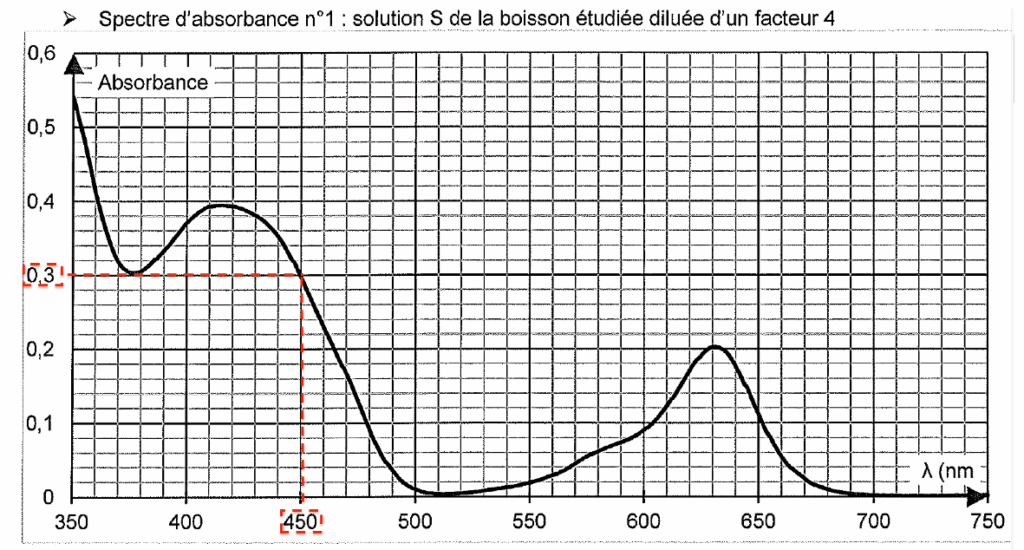
$A=8,1 \times 10^{3}\ C$
$C_{diluée}=\frac{A}{8,1 \times 10^{3}}=\frac{0,30}{8,1 \times 10^{3}}=3,7 \times 10^{-5}\ \text{mol.L}^{-1}$
La solution S est diluée d’un facteur 4 :
$C=4 \times C_{diluée}=4 \times 3,7 \times 10^{-5}=1,5 \times 10^{-4}\ \text{mol.L}^{-1}$
Déterminons la masse de colorant E102 contenue dans un verre :
$n=\frac{m}{M}\ \Rightarrow\ m=n \times M$
Or $n=C \times V$ donc $m=C \times V \times M$
$m=1,5 \times 10^{-4} \times 3,0{.10}^{-2} \times 534$
$m=2,4 \times 10^{-3}\ \text{g}$
$m=2,4\ \text{mg}$
La DJA est $7,5\ \text{mg.kg}^{-1}\ \text{jour}^{-1}$. Pour une personne de $70\ \text{kg}$ :
$DJA:\ m_{max}=70 \times 7,5=525\ \text{mg}$
| 1 verre | 2,4 mg |
| N verres | 525 mg |
$N=\frac{525 \times 1}{2,4}=219$
Cette personne peut boire $219$ verres avant d’atteindre la dose journalière admissible. Il n’y a donc aucun danger.
