Bac Métropole mars 2023 Sujet 2
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°23-PYCJ2ME1
Sujet et corrigé
EXERCICE 1 – ÉTUDE DE LA VITAMINE C CONTENUE DANS LES KIWIS (9 points)
L’acide ascorbique, couramment appelé vitamine C, intervient dans de nombreux processus métaboliques dans le corps humain. Comme l’organisme ne peut ni la synthétiser ni la stocker, les apports en vitamine C doivent se faire par l’alimentation.
Les kiwis jaunes et les kiwis verts font partie des fruits les plus riches en acide ascorbique. L’agence nationale de sécurité sanitaire de l’alimentation recommande un apport minimum en vitamine C de 110 mg par jour pour un adulte.

L’objectif de cet exercice est d’étudier les propriétés de l’acide ascorbique et de déterminer la quantité de kiwis nécessaire aux besoins journaliers d’un adulte en vitamine C.
Données :
- formule brute de l’acide ascorbique : C6H8O6 ;
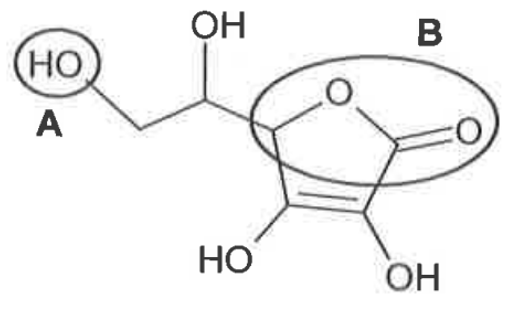
- formule topologique de l’acide ascorbique (ci-contre) ;
- masse molaire de l’acide ascorbique : M = 176 g·mol–1 ;
- couple acide-base associé à l’acide ascorbique : C6H8O6(aq) / C6H7O6–(aq) ;
- concentration standard : c° = 1,0 mol·L–1 ;
- données de spectroscopie infrarouge :
| Liaison | O–H | C–H | C=C | C=O |
| Nombre d’onde (en cm–1) | 3200 – 3700 | 2850 – 3100 | 1620 – 1680 | 1650 – 1730 |
| Allure de la bande caractéristique | Forte et large | Forte | Faible et fine | Forte et fine |
1. Quelques propriétés de l’acide ascorbique
Q1. Représenter la formule semi-développée de l’acide ascorbique puis nommer les familles fonctionnelles associées aux groupes A et B entourés sur la formule topologique.
Formule semi développée acide ascorbique
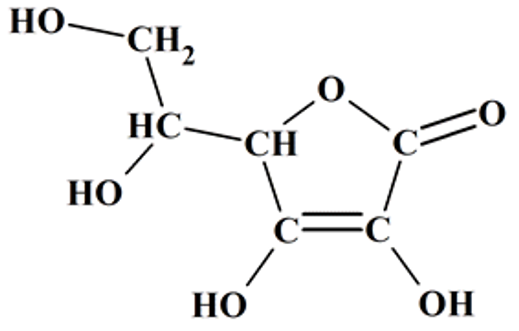
Famille fonctionnelle associée au groupe A : Alcool
Famille fonctionnelle associée au groupe B : Ester
Q2. Justifier que le spectre infrarouge de la figure 1 est compatible avec la structure de l’acide ascorbique.
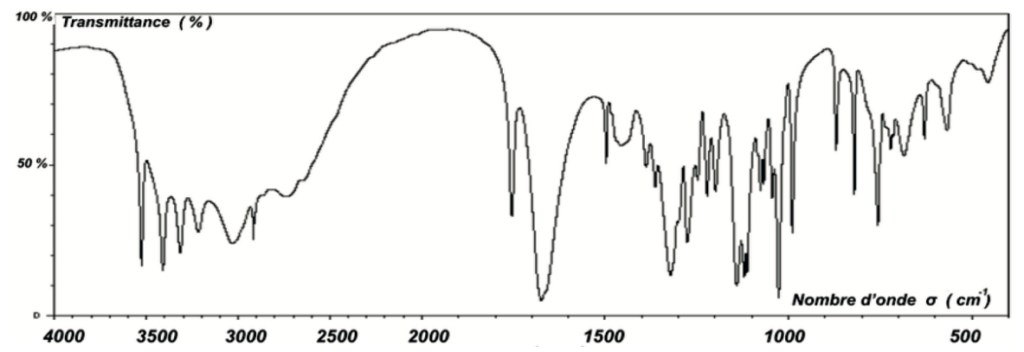
Figure 1. Spectre infrarouge de l’acide ascorbique

L’acide ascorbique comporte :
- des liaisons O-H (nombre d’onde entre 3200 et 3700 cm-1 Forte et large)
- une liaison C=O (nombre d’onde entre 1650 et 1750 cm-1 Forte et fine)
- une liaison C=C (nombre d’onde entre 1620 et 1680 cm-1 Faible et fine)
- des liaisons C-H (nombre d’onde entre 2850 et 3100 cm-1 Forte).
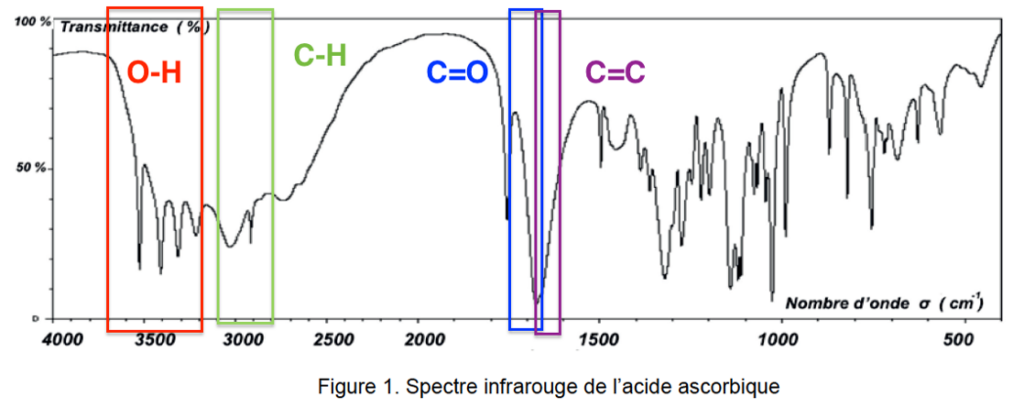
Le spectre infrarouge de la figure 1 comporte ces bandes caractéristiques : il est compatible avec la structure de l’acide ascorbique.
Pour étudier les propriétés acidobasiques de la vitamine C, on dissout 1,0 g d’acide ascorbique commercial dans une fiole jaugée de 50 mL puis on complète jusqu’au trait de jauge avec de l’eau distillée. La mesure du pH de la solution donne pH = 2,6.
Q3. Déterminer la quantité de matière initiale n0 d’acide ascorbique introduite dans la fiole jaugée.
${n}_{0}=\frac{{m}_{0}}{{M}}$
${n}_{0}=\frac{{1},{0}}{{176}}$
${n}_{0}={5},{7}\times{10}^{-{3}}\ {mol}$
La transformation entre l’acide ascorbique et l’eau est modélisée par la réaction d’équation :
C6H8O6(aq) + H2O(ℓ) ⇆ C6H7O6–(aq) + H3O+(aq)
Q4. Donner la définition d’un acide faible.
Un acide faible est un acide qui ne réagit pas totalement avec l’eau.
Q5. Montrer que l’acide ascorbique est un acide faible dans l’eau.
Méthode 1 :
Construisons un tableau d’avancement :
| $C_6{H_8O_6}{(aq)}\ $ | $\ H_2O{(l)}$ | $\rightleftarrows\ C_6{H_7O_6^-}{(aq)}\ $ | $+\ {H_3O}{(aq)}^+$ | |
| Etat initial | $n_0-x$ | Solvant | 0 | 0 |
| Etat intermédiaire | $n_0-x$ | Solvant | $x$ | $x$ |
| Etat final | $n_0-x_f$ | Solvant | $x_f$ | $x_f$ |
$x_f=n_{H_3O^+}=\left[H_3O^+\right]\times V$
$x_f=\left[H_3O^+\right]\times V$
$x_f=c^0\times{10}^{-pH}\times V$
$x_f=1,0\times{10}^{-2,6}\times 50\times{10}^{-3}$
$x_f=1,3\times{10}^{-4}\ mol$
$n_0-x_{max}=0$
$x_{max}=n_0$
$x_{max}=5,7\times{10}^{-3}\ mol$
$\tau=\frac{x_f}{x_{max}}$
$\tau=\frac{1,3\times{10}^{-4}}{5,7\times{10}^{-3}}$
$\tau=0,023$
$\tau\neq1$ : la réaction entre l’acide ascorbique et l’eau est limitée : l’acide ascorbique est donc un acide faible.
Méthode 2 :
$-\log(c)=-\log\left(\frac{n_0}{V}\right)$
$-\log\left(c\right)=-\log\left(\frac{5,7\times{10}^{-3}}{50\times{10}^{-3}}\right)=0,94$
$-\log\left(c\right)\neq pH$ : L’acide ascorbique est donc un acide faible.
Q6. Donner l’expression de la constante d’acidité KA du couple associé à l’acide ascorbique en fonction des concentrations [C6H8O6], [C6H7O6–], [H3O+] à l’équilibre et de la concentration standard c° puis montrer que la valeur du pKA est proche de 4,2.
$K_A=\frac{\left[C_6H_7O_6^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[C_6H_8O_6\right]_{eq}\times c^0}$
Or, d’après le tableau d’avancement :
$\left[H_3O^+\right]{eq}=\frac{x_f}{V}$
$\left[C_6H_7O_6^-\right]{eq}=\frac{x_f}{V}=\left[H_3O^+\right]{eq}$
$\left[C_6H_8O_6\right]{eq}=\frac{n_0-x_f}{V}=\frac{n_0}{V}-\frac{x_f}{V}=\frac{n_0}{V}-\left[H_3O^+\right]_{eq}$
$K_A=\frac{\left[H_3O^+\right]{eq}\times\left[H_3O^+\right]{eq}}{\left(\frac{n_0}{V}-\left[H_3O^+\right]_{eq}\right)\times c^0}$
$K_A=\frac{\left[H_3O^+\right]^2}{\left(\frac{n_0}{V}-\left[H_3O^+\right]\right)\times c^0}$
Or
$\left[H_3O^+\right]=c^0\times{10}^{-pH}$
$K_A=\frac{\left(c^0\times{10}^{-pH}\right)^2}{\left(\frac{n_0}{V}-c^0\times{10}^{-pH}\right)\times c^0}$
$K_A=\frac{\left(1,0\times{10}^{-2,6}\right)^2}{\left(\frac{5,7\times{10}^{-3}}{50\times{10}^{-3}}-1,0\times{10}^{-2,6}\right)\times1,0}$
$K_A=5,7\times{10}^{-5}$
${\rm pK}_A=-\log\left(K_A\right)$
${\rm pK}_A=-\log\left(5,7\times{10}^{-3}\right)$
${\rm pK}_A=4,2$
2. Acide ascorbique dans un kiwi jaune
Pour déterminer la concentration en acide ascorbique d’un kiwi jaune, on le mixe jusqu’à en obtenir du jus dont le pH est de 3,5.
Q7. Déterminer l’espèce acide-base prédominante associée à l’acide ascorbique présente dans le jus d’un kiwi jaune.
Diagramme de prédominance :

$\left[C_6H_8O_6\right]>\left[C_6H_7O_6^-\right]$ $\left[C_6H_7O_6^-\right]>\left[C_6H_8O_6\right]$
pH = 3,5: $C_6H_8O_6$ prédomine dans le jus de kiwi jaune.
La quantité d’acide ascorbique présent dans un kiwi jaune est déterminée à l’aide d’un dosage par excès. Le principe de ce dosage est le suivant :
- on met le jus de kiwi en présence d’une quantité connue de diiode I2. Seul l’acide ascorbique réagit avec le diiode, introduit en excès ;
- on détermine ensuite par titrage la quantité de diiode restant ;
- on en déduit alors la quantité d’acide ascorbique dans le kiwi jaune.
Protocole du dosage
- Étape 1 : réaction de l’acide ascorbique avec le diiode
Introduire la totalité du jus d’un kiwi jaune mixé dans une fiole jaugée de 250 mL, puis compléter avec de l’eau distillée jusqu’au trait de jauge. On appelle S la solution ainsi obtenue.
Introduire dans un erlenmeyer un volume V = 50,0 mL de la solution S, ainsi qu’un volume V1 = 20,0 mL d’une solution aqueuse de diiode I2 à la concentration C1 = 2,9×10–2 mol∙L–1.
Cette transformation peut être modélisée par la réaction d’équation suivante :
C6H8O6(aq)+ I2(aq) → C6H6O6(aq)+ 2 I–(aq)+ 2 H+(aq)
- Étape 2 : titrage du diiode restant par les ions thiosulfate S2O32−
Titrer le contenu de l’erlenmeyer préparé lors de l’étape 1 par une solution aqueuse de thiosulfate de sodium de concentration C2 = 5,00×10–2 mol∙L–1, en présence d’un indicateur coloré spécifique au diiode.
On obtient un volume à l’équivalence V2 = 16,5 mL.
La transformation mise en jeu lors du titrage peut être modélisée par la réaction d’équation suivante :
I2 (aq) + 2 S2O32−(aq) → S4O62−(aq) + 2 I−(aq)
Q8. En exploitant le résultat du titrage, montrer que la quantité de matière de diiode dosé lors de l’étape 2 est égale à 4,13×10−4 mol.
Équation de la réaction support du titrage :
${I_2}{(aq)}+2S_2{O_3^{-2}}{(aq)}\rightarrow S_4{O_6^{-2}}{(aq)}+2I{(aq)}^-$
A l’équivalence :
$\frac{n_{I_2\ dosé}}{1}=\frac{n_{S_2O_3^{-2}\ eq}}{2}$
$n_{I_2\ dosé}=\frac{C_2\times V_2}{2}$
$n_{I_2\ dosé}=\frac{5,00\times10^{-2}\times16,5\times10^{-3}}{2}$
$n_{I_2\ dosé}=4,13\times10^{-4}\ mol$
Q9. Après avoir calculé la masse d’acide ascorbique contenue dans un kiwi jaune, déterminer combien il faudrait en manger pour satisfaire les besoins journaliers en acide ascorbique d’un adulte.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
$C_6{H_8O_6}{(aq)}+{I_2}{(aq)}\rightarrow C_6{H_6O_6}{(aq)}+2I{(aq)}^-+2H_{(aq)}^+$
D’après cette équation :
$\frac{n_{{C_6H}8O_6}}{1}=\frac{n{I_2^{réagit}}}{1}$
Or
$n_{I_2}^{réagit}=n_{I_2}^{initial}-n_{I_2}^{dosé}$
$n_{{C_6H}8O_6}=n{I_2}^{initial}-n_{I_2}^{dosé}$
Avec :
$n_{I_2}^{initial}=C_1\times V_1$
$n_{{C_6H}8O_6}=C_1\times V_1-n_{I_2}^{dosé}$
$n_{{C_6H}8O_6}=2,9\times{10}^{-2}\times20,0\times{10}^{-3}-4,13\times{10}^{-4}$
$n{{C_6H}_8O_6}=1,67\times{10}^{-4}\ mol$
Calculons la masse d’acide ascorbique :
$m_{C_6H_8O_6}=n_{C_6H_8O_6}\times M_{C_6H_8O_6}$
$m_{C_6H_8O_6}=1,67\times{10}^{-4}\times176$
$m_{C_6H_8O_6}=2,94\times{10}^{-2}\ g$
Cette masse est celle contenue dans le prélèvement de 50,0 mL
| $2,94\times{10}^{-2}\ g$ | 50,0 mL |
| $m_{acide}$ | 250,0 mL |
$m_{acide}=\frac{250,0\times2,94\times{10}^{-2}}{50,0}$
$m_{acide}=1,47\times{10}^{-1}\ g$
Il y a 0,147 g d’acide ascorbique dans un kiwi jaune.
Besoins journaliers : 110mg
| 1 kiwi | $1,47\times{10}^{-1}\ g$ |
| N | $110\times{10}^{-3}\ g$ |
$N=\frac{110\times{10}^{-3}}{1,47\times{10}^{-1}}$
$N=0,74$
Un kiwi suffirait pour satisfaire les besoins journaliers en acide ascorbique d’un adulte.
Le même dosage est réalisé avec un kiwi vert de même masse. On obtient un nouveau volume à l’équivalence pour le titrage du diiode restant V’2 = 19,7 mL.
Q10. Expliquer sans calcul si le kiwi vert contient plus ou moins d’acide ascorbique que le kiwi jaune.
${V^\prime}_2>V_2$ : la quantité restante de $I_2$ est donc plus grande. La quantité d’acide ascorbique qui a réagit est donc inferieure à celle contenue dans un kiwi jaune.
3. Oxydation de l’acide ascorbique par le bleu de méthylène
L’acide ascorbique est un réducteur, ce qui conditionne sa conservation à l’air libre. Dans cette partie, pour des raisons pratiques, on étudie ses propriétés réductrices en le faisant réagir avec du bleu de méthylène.
Au contact du bleu de méthylène, noté BM+, l’acide ascorbique C6H8O6 contenu dans le jus de kiwi se transforme en un nouveau composé de formule brute C6H6O6.
Données :
- couple oxydant / réducteur associé à l’acide ascorbique : C6H6O6(aq) / C6H8O6(aq) ;
- couple oxydant / réducteur associé au bleu de méthylène : BM+(aq) / BMH(aq).
Q11. À l’aide des demi-équations électroniques de chacun des couples mis en jeu, établir l’équation de la réaction modélisant la transformation chimique ayant lieu entre l’acide ascorbique C6H8O6 et le bleu de méthylène BM+.
Couples :
$C_6{H_6O_6}{(aq)}/C_6{H_8O_6}{(aq)}$
$BM^+(aq)/BMH(aq)$
$C_6{H_8O_6}{(aq)}=C_6{H_6O_6}{(aq)}+2H_{(aq)}^++2e^-$
$BM^+(aq)+H_{(aq)}^++2e^-=BMH(aq)$
$C_6{H_8O_6}{(aq)}+BM^+(aq)\rightleftarrows C_6{H_6O_6}{(aq)}+BMH(aq)+H_{(aq)}^+$
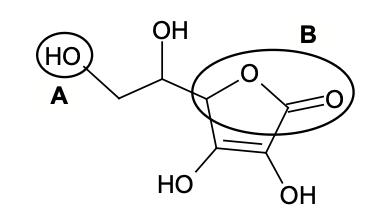
On réalise le suivi cinétique de cette réaction à deux températures différentes. Après traitement des résultats, on trace sur la figure 2 l’évolution temporelle de la concentration CASC de l’acide ascorbique, pour les deux températures choisies.
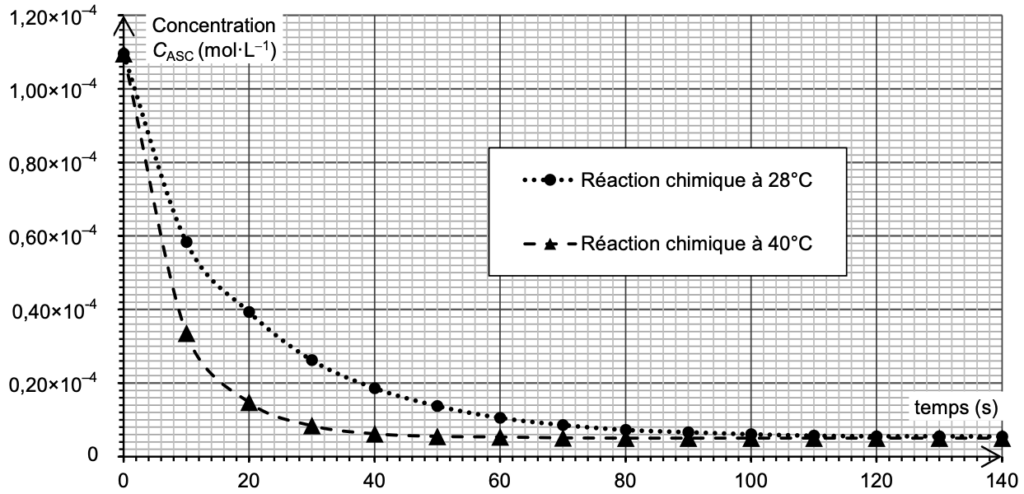
Figure 2. Évolution temporelle de la concentration CASC de l’acide ascorbique en solution
Q12. Exprimer la vitesse volumique de disparition de l’acide ascorbique en fonction de CASC puis déterminer sa valeur à l’instant initial à la température de 28 °C.
$v_d=-\frac{dC_{ASC}(t)}{dt}$
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{0-1,1\times{10}^{-4}}{20-0}=-5,5\times{10}^{-6}\ mol.L^{-1}.s^{-1}$
$v_i\ pour\ 28^\circ C=-\frac{dC_{ASC}(t)}{dt}=-k$
$v_i\ pour\ 28^\circ C=5,5\times10^{-6}\ mol.L^{-1}.s^{-1}$
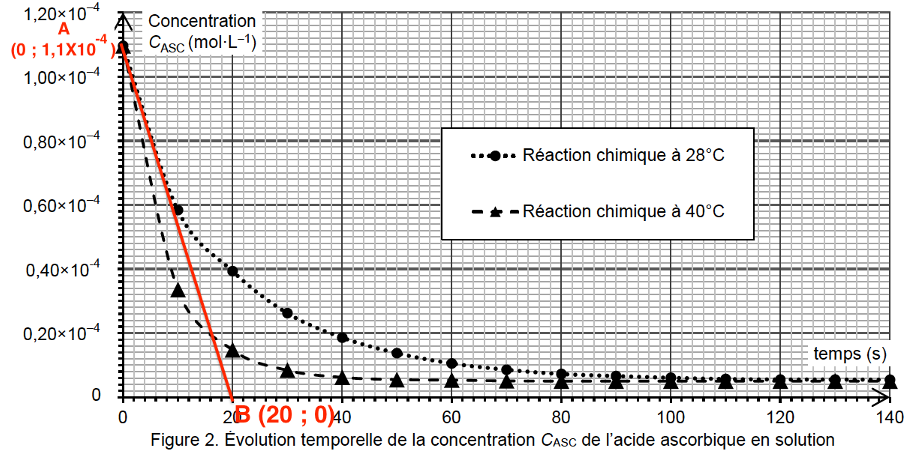
Q13. En utilisant les courbes de la figure 2, identifier en justifiant deux facteurs cinétiques de la réaction entre l’acide ascorbique et le bleu de méthylène.
1er facteur cinétique : la température. Lorsque la température est plus élevée (courbe à 40°C), la concentration du réactif diminue plus rapidement.
2nd facteur cinétique : la concentration. Au cours de la réaction le coefficient directeur de la tangente en un point diminue. Plus la concentration est faible, plus la vitesse de réaction est petite.