Polynésie 2025 Sujet 2
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°25-PYCJ2PO1
Le télescope spatial James Webb (noté JWST) est un télescope développé par la NASA avec la participation de l’Agence Spatiale Européenne et de l’Agence Spatiale Canadienne. Ce télescope JWST se trouve en permanence à une distance de 1,5 millions de kilomètres du centre de la Terre au point de Lagrange noté L2.
Pour le système Terre-Soleil, il existe 5 positions appelées points de Lagrange notés de L1 à L5 (voir figure 1). Sous l’effet de l’action du Soleil et de la Terre, un satellite placé sur l’un de ces points a un mouvement de rotation autour du Soleil de même période que celle de la Terre. Les positions relatives du satellite, du Soleil et de la Terre restent alors inchangées au cours du temps.
Cette position assure au télescope JWST de demeurer pendant toute l’année dans l’ombre portée de la Terre et donc à l’abri du rayonnement thermique du Soleil.
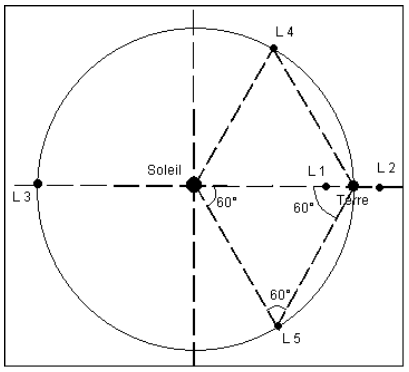
Figure 1. Les points de Lagrange.
Les objectifs de cet exercice sont de déterminer la période de révolution du télescope JWST et d’analyser une méthode de détermination de la distance à laquelle se trouve une galaxie.
Données :
- distance Terre – Soleil : DT-S = 149,6 × 106 km ;
- distance Terre – JWST : DT-J = 1,511 × 106 km ;
- masse de JWST : mJ = 6,17 × 103 kg ;
- masse de la Terre : MT = 5,97 × 1024 kg ;
- masse du Soleil : MS = 1,99 × 1030 kg ;
- constante de gravitation universelle : G = 6,67×10–11 N·m2·kg–2.
Mouvement orbital du télescope JWST.
Q1. Indiquer les raisons pour lesquelles il n’aurait pas été judicieux de placer le télescope JWST au point de Lagrange L1 (voir figure 1).
Q2. Représenter, sans souci d’échelle, l’alignement du Soleil, de la Terre et du télescope JWST situé en L2. Ces trois corps seront représentés par des points notés S, T et J. Faire apparaître sur la figure la distance Terre – Soleil notée DT-S et la distance Terre – JWST notée DT-J. Calculer la distance DS-J du Soleil au télescope JWST.
Q3. Exprimer la force d’attraction gravitationnelle, notée FT-J, qu’exerce la Terre sur le télescope JWST en fonction de G, mJ, MT et DT-J puis la calculer.
La force d’attraction gravitationnelle, notée $\overrightarrow{F}_{S-J}$, qu’exerce le Soleil sur le télescope JWST a pour valeur $F_{S-J} = 35,9\ \text{N}$.
Q4. Représenter, sur le schéma réalisé à la question Q2 et sans souci d’échelle, le overrightarrowteur $\overrightarrow{F}_{T-J}$ représentant la force exercée par la Terre sur le télescope JWST et le overrightarrowteur $\overrightarrow{F}_{S-J}$ représentant la force exercée par le Soleil sur le télescope JWST.
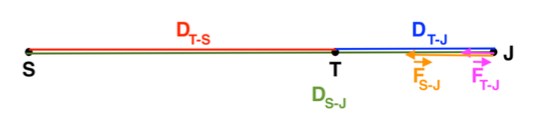
On note $\overrightarrow{F}$ la force correspondant à la résultante des forces $\overrightarrow{F}_{T-J}$ et $\overrightarrow{F}_{S-J}$ agissant sur le télescope JWST ; on a donc $\overrightarrow{F} = \overrightarrow{F}_{T-J} + \overrightarrow{F}_{S-J}$
Q5. Vérifier que la valeur de la force $\overrightarrow{F}$ vaut approximativement F = 37,0 N.
On admet que le centre de masse du télescope JWST a une trajectoire circulaire de rayon DS-J = 151,1×106 km centrée sur le Soleil. La Terre, le Soleil et le télescope JWST restent alignés en permanence.
La force de gravitation totale exercée sur le télescope JWST peut s’exprimer à l’aide de la relation :
$$F = Gm_J \cdot \left(\frac{M_S}{D_{S-J}^2} + \frac{M_T}{D_{T-J}^2}\right)$$
Pour simplifier les calculs, on introduit la distance effective Deff entre le Soleil et le télescope JWST, définie par la relation :
$$F = Gm_J \cdot \frac{M_S}{D_{\text{eff}}^2}$$
Q6. Exprimer la distance effective Deff en fonction de MS, MT, DS-J et DT-J et vérifier que cette distance effective a pour valeur Deff = 1,49×1011 m.
Q7. Sur un schéma représentant la trajectoire circulaire du télescope JSWT, représenter, sans souci d’échelle, les overrightarrowteurs $\overrightarrow{u}_n$ et $\overrightarrow{u}_t$ du repère de Frenet, respectivement normal et tangent à la trajectoire, au niveau du télescope JWST. Représenter également la force $\overrightarrow{F}$.
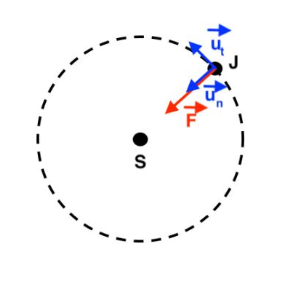
L’accélération du télescope JWST s’écrit $\overrightarrow{a} = a_n \overrightarrow{u}_n + a_t \overrightarrow{u}_t$.
Q8. Donner l’expression de l’accélération normale an du télescope JWST en fonction de la vitesse v et du rayon de la trajectoire DS-J.
Dans la situation particulière étudiée, la force d’attraction gravitationnelle $\overrightarrow{F}$ qu’exercent le Soleil et la Terre sur le télescope JWST peut s’écrire :
$$\overrightarrow{F} = G\cdot \frac{m_J\cdot M_S}{D_{\text{eff}}^2}\ \overrightarrow{u}_n$$
Q9. En appliquant la deuxième loi de Newton dans le référentiel d’étude, supposé galiléen, déterminer l’expression du vecteur accélération du centre de masse du télescope JWST en fonction de $G$, $M_S$, $D_{\text{eff}}$ et $\overrightarrow{u}_n$.
Q10. Montrer que la vitesse v du télescope JWST s’écrit :
$$v = \sqrt{\frac{G\cdot M_S \cdot D_{S-J}}{D_{\text{eff}}^2}}$$
Q11. En déduire que la période de révolution $T$ du télescope JWST est donnée par la relation $T=2\pi \sqrt{\frac{D_{S-J}\cdot D_{\text{eff}}^2}{G\cdot M_S}}$. Calculer sa valeur en jours et vérifier la cohérence aoverrightarrow la valeur attendue.
Vitesse d’éloignement de la galaxie TGS153Z170.
La mesure du déplacement vers le rouge, par effet Doppler, de raies caractéristiques des spectres émis par des sources lointaines (galaxies, quasars, etc.) est la preuve d’un univers en expansion, aussi bien que le moyen de mesurer la vitesse d’éloignement de ces objets lointains. En faisant appel à des modèles cosmologiques, on peut tirer des informations sur la distance de ces sources à la Terre.
D’après Boratav & R. Kerner, Relativité, Ellipse, 1991
Spectre d’émission de l’hydrogène acquis sur Terre à l’aide d’une source immobile présente au laboratoire.
Spectre de la galaxie TGS153Z170 avec indexage des raies Hα, Hβ et Hɣ de l’hydrogène.
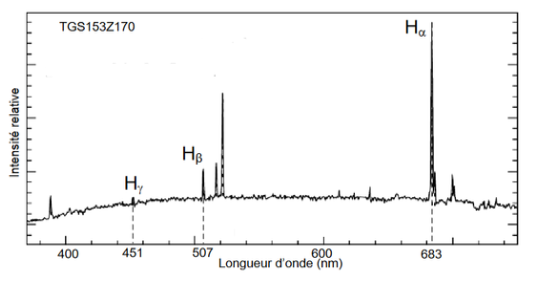
Source M. Colless et al. The 2dF Galaxy Redshift Survey)
Le télescope JWST est sensible aux longueurs d’onde comprises entre 0,6 µm et 28 µm.
Q12. Indiquer, en justifiant, la raison pour laquelle seule la raie Ha de l’atome d’hydrogène émise par la galaxie TGS153Z170 peut être observée par le télescope JWST.
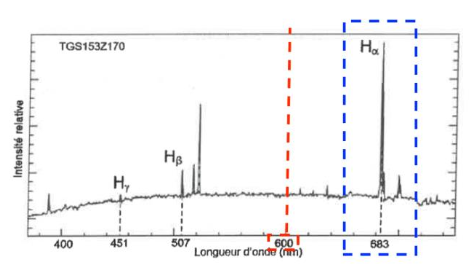
La longueur d’onde de la raie Hα dans le cas d’une source présente au laboratoire est notée $\lambda_H$ et sa fréquence associée $f_H$. Dans le cas d’une source présente dans la galaxie TGS153Z170 la longueur d’onde apparente de la raie Hα et notée $\lambda’_H$ et sa fréquence $f’_H$.
Q13. Préciser si la valeur de f’H est plus grande ou plus petite que la valeur de fH et indiquer si la galaxie TGS153Z170 d’éloigne ou se rapproche de la Terre.
On souhaite déterminer la vitesse de déplacement vGal de la galaxie TGS153Z170 par rapport à la Terre. Dans ce cas particulier, la relation entre les longueurs d’onde λH et λ‘H est donnée par la formule (1) ci-dessous.
$$\lambda’_H = \lambda_H \cdot \left(1 + \frac{v{\text{Gal}}}{c}\right)\qquad (1)$$
avec vGal la vitesse de déplacement de la galaxie TGS153Z170 par rapport à la Terre et c la célérité de la lumière dans le vide.
Donnée : célérité de la lumière dans le vide : c = 3,00×108 m·s–1.
Q14. À l’aide de la formule (1) ci-dessus, exprimer puis calculer la vitesse de déplacement vGal de la galaxie TGS153Z170 par rapport à la Terre.
En astrophysique, la loi de Hubble-Lemaître énonce que les galaxies s’éloignent les unes des autres à une vitesse approximativement proportionnelle à leur distance. Autrement dit, plus une galaxie est loin de nous, plus elle semble s’éloigner rapidement.
La loi de Hubble-Lemaître a pour expression : vGal = H0·D, où :
- vGal est la vitesse d’éloignement de la galaxie en m·s–1 par rapport à la Terre ;
- H0 est la constante de Hubble avec H0 = 70×103 m·s−1·Mpc−1 ;
- D est la distance entre la Terre et la galaxie en Mpc (Mégaparsec).
Donnée : unité de distance le Mégaparsec : 1 Mpc = 3,1×1022 m.
Q15. Calculer, en Mégaparsec puis en mètres, la distance D à laquelle la galaxie TGS153Z170 se trouve de la Terre.