Bac Métropole Septembre 2023 Sujet 2
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°23-PYCJ2ME3
Sujet et corrigé
EXERCICE 1 – JUSTE UNE IMPRESSION GUSTATIVE ? (9 points)
Il existe plus de 7 000 variétés de pommes à la texture et au goût variés. Lors de leur dégustation, certaines semblent plus acides que d’autres, entraînant une sensation moins sucrée en bouche.
L’objectif de cet exercice est de comparer la teneur en sucre et en acide de jus de plusieurs variétés de pommes, afin de voir s’il existe un lien entre ces deux teneurs et l’impression gustative que ces pommes laissent en bouche.

1. Étude de l’acidité d’un jus de pomme Granny Smith
Une pomme contient différents acides comme l’acide malique, l’acide tartrique et l’acide citrique. L’acide malique étant majoritairement présent, on émet l’hypothèse dans cette première partie qu’il est le seul acide présent dans le jus de pomme étudié.
Données :
- formule semi-développée de l’acide malique :
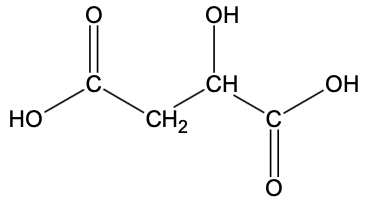
- l’acide malique C4H6O5 est un diacide que l’on notera H2A ;
- masse molaire de l’acide malique : M(H2A) = 134,0 g·mol–1 ;
- valeurs des pKA à 25 °C des couples acide-base associés à l’acide malique :
- H2A(aq) / HA–(aq) : pKA1 = 3,5 ;
- HA–(aq) / A2–(aq) : pKA2 = 5,1.
Q1. Représenter la formule topologique de la molécule d’acide malique, puis entourer les groupes caractéristiques et nommer les familles fonctionnelles correspondantes.
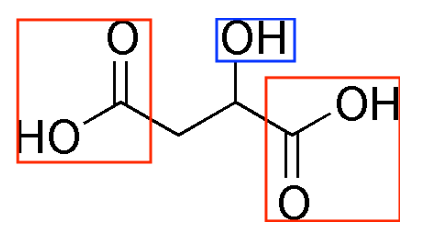
Formule topologique de la molécule d’acide malique :
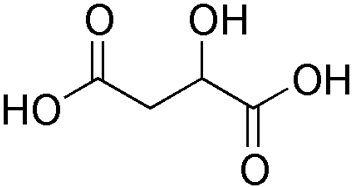
Familles fonctionnelles
OH : Alcool
COOH : acide carboxylique
On souhaite déterminer la concentration en masse d’acide malique dans le jus de pomme étudié. Pour cela on réalise un titrage, avec suivi pH-métrique, d’un volume VA = 20,0 mL de ce jus par une solution aqueuse d’hydroxyde de sodium de concentration CB = 1,0×10–1 mol·L–1.
Q2. Schématiser et légender le montage permettant de réaliser ce titrage, en indiquant le nom et la position des espèces titrante et titrée.
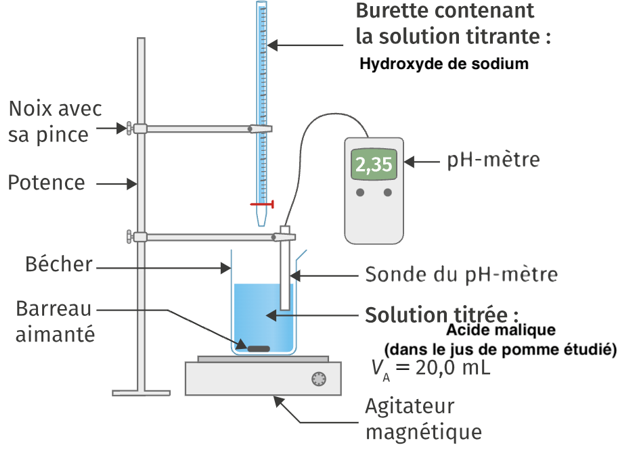
La courbe obtenue lors du titrage de l’acide malique dans le jus de pomme Granny Smith est donnée en figure 1.
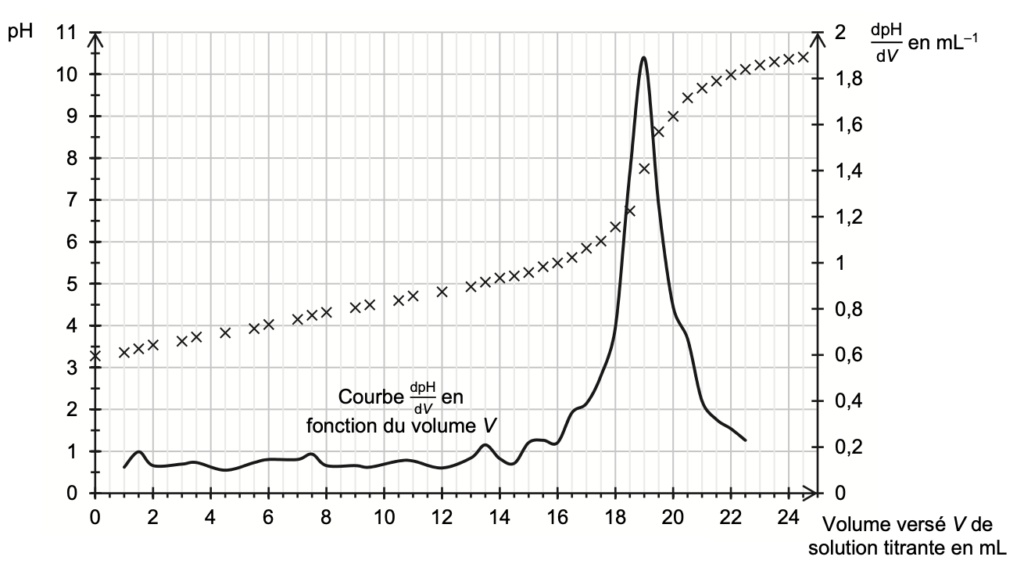
Figure 1. Courbe de titrage par suivi pH-métrique
Q3. Établir le diagramme de prédominance des différentes formes acide-base associées à l’acide malique.
- H2A(aq) / HA–(aq) : pKA1 = 3,5 ;
- HA–(aq) / A2–(aq) : pKA2 = 5,1.
Diagramme de prédominance :

Q4. Déterminer graphiquement le pH de la solution à la fin du titrage. Identifier alors, parmi les deux équations proposées ci-dessous, la réaction support du titrage :
(1) H2A(aq) + HO–(aq) → AH–(aq) + 2 H2O(ℓ)
(2) H2A(aq) + 2 HO–(aq) → A2–(aq) + 2 H2O(ℓ)
Graphiquement, à la fin du titrage : pH=10,5.
Pour pH=10,5, l’espèce A2– est prédominante (Q3).
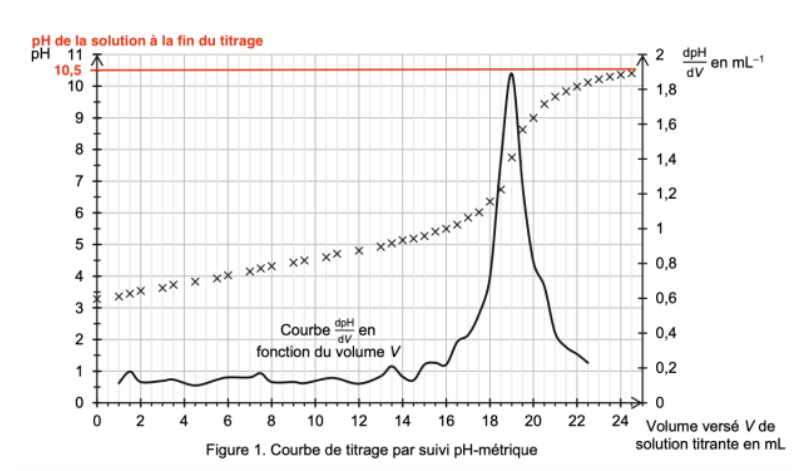
Ainsi, la réaction support du titrage produit l’espèce A2–.
La réaction support du titrage est la réaction (2) : H2A(aq) + 2 HO–(aq) → A2–(aq) + 2 H2O(ℓ)
Q5. Montrer que la concentration en masse d’acide malique dans le jus de pomme étudié est de 6,4 g·L–1.
H2A(aq) + 2 HO–(aq) → A2–(aq) + 2 H2O(ℓ)
A l’équivalence :
$\frac{n_{H_2A}^i}{1}=\frac{n_{HO^-}^{eq}}{2}$
$C_AV_A=\frac{C_BV_{eq}}{2}$
$C_A=\frac{C_BV_{eq}}{V_A}$
$C_A=\frac{C_BV_{eq}}{2\times V_A}$
On détermine graphiquement $V_{eq}$ qui se repère au maximum de la courbe $\frac{dpH}{dV}$ :
$V_{eq}=19,0\ mL$
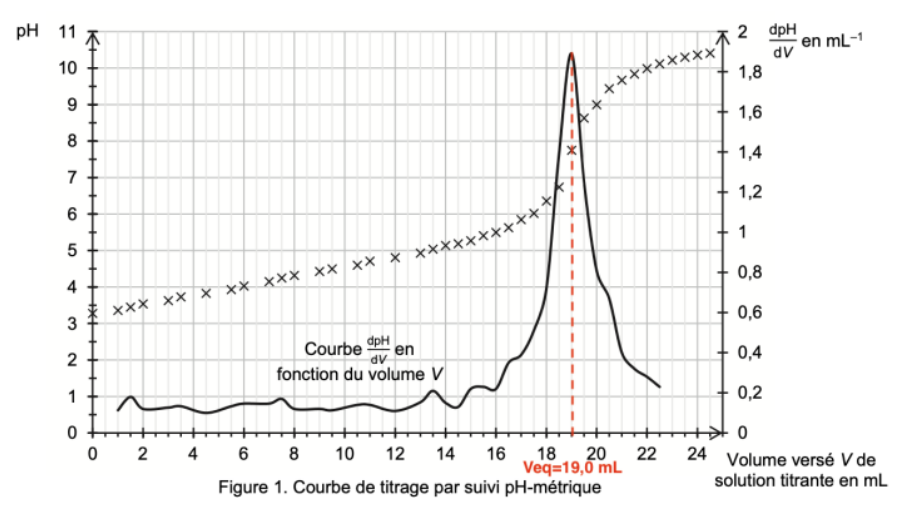
$C_A=\frac{1,0{\times10}^{-1}\times19,0{\times10}^{-3}}{2\times20,0{\times10}^{-3}}$
$C_A=4,8{\times10}^{-2}\ mol{.L}^{-1}$
$C_{mA}=C_A\times M$
$C_{mA}=4,8{\times10}^{-2}\times134,0$
$C_{mA}=6,4\ g{.L}^{-1}$
2. Dosage du glucose dans le jus de pomme Granny Smith
Une pomme contient différents sucres, notamment le glucose de formule brute C6H12O6. Dans cette partie, on souhaite doser le glucose présent dans le jus de pomme Granny Smith identique à celui de la partie 1.
Données :
- protocole expérimental :
- introduire 10,0 mL de jus de pomme dans une fiole jaugée de 50 mL, puis compléter avec de l’eau distillée jusqu’au trait de jauge. On obtient la solution nommée S0 ;
- introduire, dans un bécher, 10,0 mL de solution S0, puis ajouter 20,0 mL d’une solution aqueuse de diiode, de concentration [I2] = 5,0×10–2 mol·L–1, et une solution aqueuse d’hydroxyde de sodium jusqu’à obtenir un volume V1 = 75,0 mL. Mettre sous agitation pendant 60 minutes. On appelle S1 la solution obtenue.
- on modélise la transformation ayant lieu dans la solution S1, supposée totale, par la réaction d’équation :
I2(aq) + 3 HO–(aq) + C6H12O6(aq) ⟶ C6H11O7–(aq) + 2 H2O(ℓ) + 2 I–(aq)
- une solution aqueuse de diiode est de couleur jaune-brun et les autres espèces présentes sont incolores en solution aqueuse ;
- masse molaire du glucose : M(C6H12O6) = 180,2 g·mol–1 ;
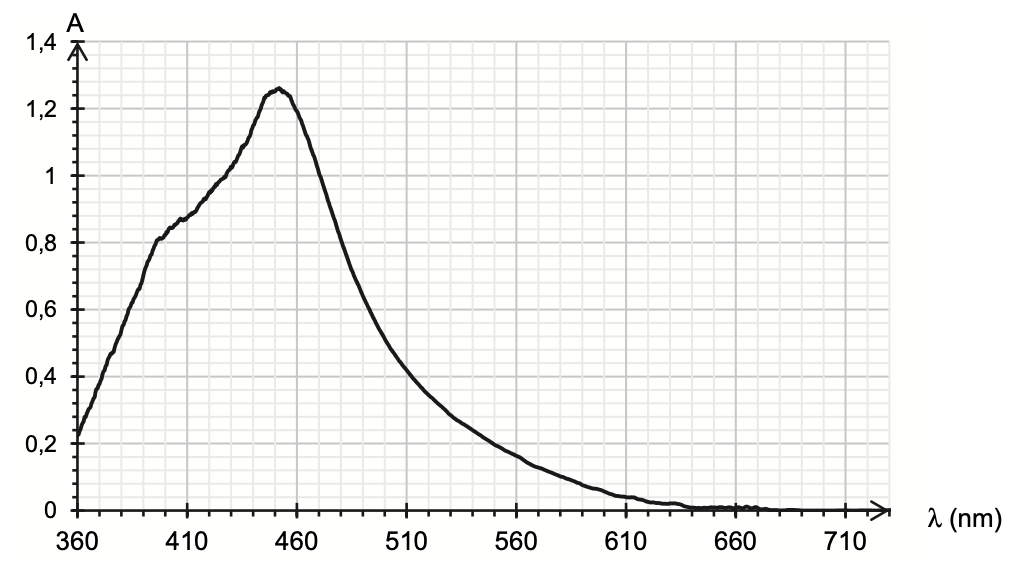
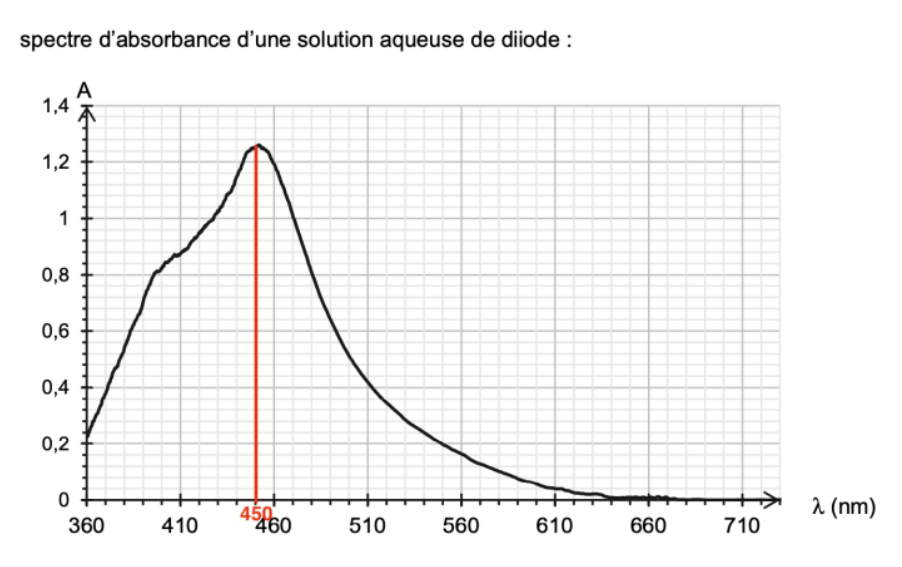
- spectre d’absorbance d’une solution aqueuse de diiode :
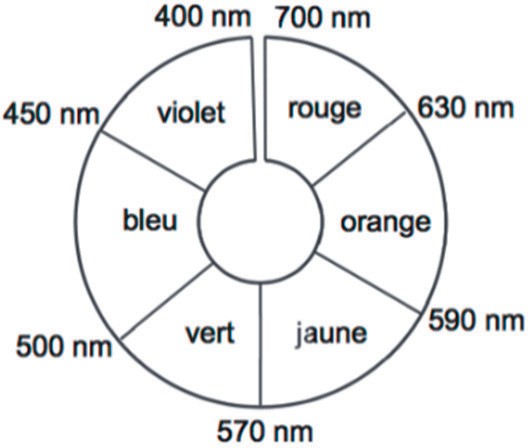
- cercle chromatique :
Q6. Montrer que la quantité de matière de diiode n0(I2) initialement présente dans la solution S1 est proche de 1,0×10–3 mol.
$\left[I_2\right]=\frac{n_0\left(I_2\right)}{V}$
$\frac{n_0\left(I_2\right)}{V}=\left[I_2\right]$
$n_0\left(I_2\right)=\left[I_2\right]\times V$
$n_0\left(I_2\right)=5,0\times{10}^{-2}\times20\times{10}^{-3}$
$n_0\left(I_2\right)=1,0\times{10}^{-3}\ mol$
Q7. Sachant que le glucose est le réactif limitant de la réaction ayant lieu dans la solution S1, montrer que la relation entre la quantité de matière finale de diiode nf(I2), la quantité de matière initiale de glucose n0(C6H12O6) et la quantité de matière initiale de diiode n0(I2), est :
n0(C6H12O6) = n0(I2)- nf(I2)
| $I_2(aq)\$ | $+\ 3\ {\rm HO}^-\left(aq\right)$ | $+\ C_6H_{12}O_6\left(aq\right)$ | $\rightarrow\ C_6H_{11}O_7^-\left(aq\right)\ $ | $+\ 2H_2O\left(l\right)\ $ | $+\ 2I^-\left(aq\right)$ | |
| État initial | $n_0\left(I_2\right)$ | Excès | $n_0\left(C_6H_{12}O_6\right)$ | 0 | Solvant | 0 |
| État intermédiaire | $n_0\left(I_2\right)-x$ | Excès | $n_0\left(C_6H_{12}O_6\right)-x$ | x | Solvant | 2x |
| État final $x_f=x_{max}$ (Réaction totale) | $n_0\left(I_2\right)-x_{max}=n_f\left(I_2\right)$ | Excès | $n_0\left(C_6H_{12}O_6\right)-x_{max}=0$ | xf | Solvant | 2xf |
D’après le sujet : « le glucose est le réactif limitant »
$n_0\left(C_6H_{12}O_6\right)-x_{max}=0$
$n_0\left(C_6H_{12}O_6\right)=x_{max}$
Or
$n_0\left(I_2\right)-x_{max}=n_f\left(I_2\right)$
$-x_{max}=n_f\left(I_2\right)-n_0\left(I_2\right)$
$x_{max}=-n_f\left(I_2\right)+n_0\left(I_2\right)$
$x_{max}=n_0\left(I_2\right)-n_f\left(I_2\right)$
Ainsi :
$n_0\left(C_6H_{12}O_6\right)=n_0\left(I_2\right)-n_f\left(I_2\right)$
On veut déterminer la quantité de matière nf(I2) dans la solution S1 à l’aide d’un dosage spectrophotométrique selon le protocole décrit ci-dessous.
- Diluer la solution S1 d’un facteur 10, on obtient la solution S2.
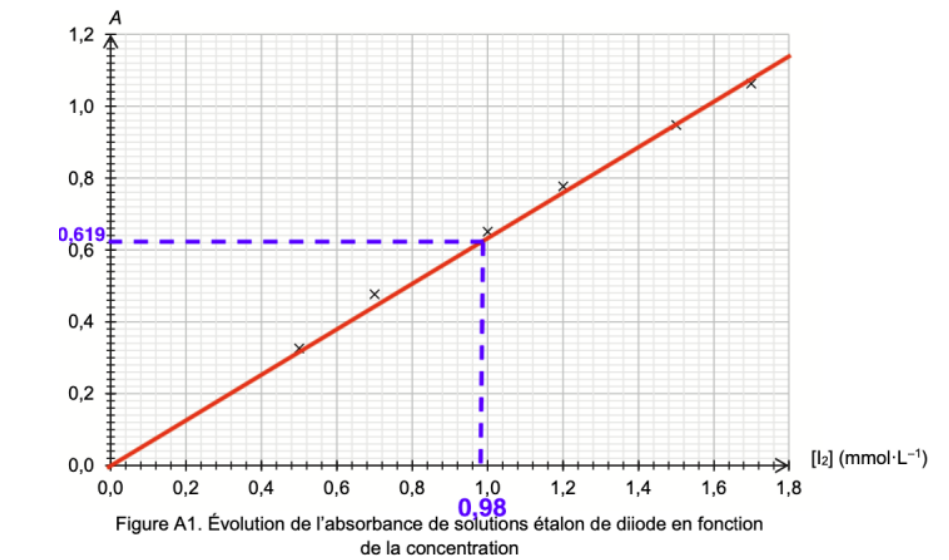
- Préparer 6 solutions étalons de concentrations connues en diiode I2 et en mesurer l’absorbance à la longueur d’onde appropriée ; les mesures sont reportées sur le graphe de la figure A1 de l’ANNEXE 1 À RENDRE AVEC LA COPIE.
- Mesurer l’absorbance de la solution S2 à la même longueur d’onde.
On mesure une valeur d’absorbance A = 0,619 pour la solution S2.
Q8. Justifier la couleur de la solution aqueuse de diiode.
$\lambda_{max}=450\ nm$
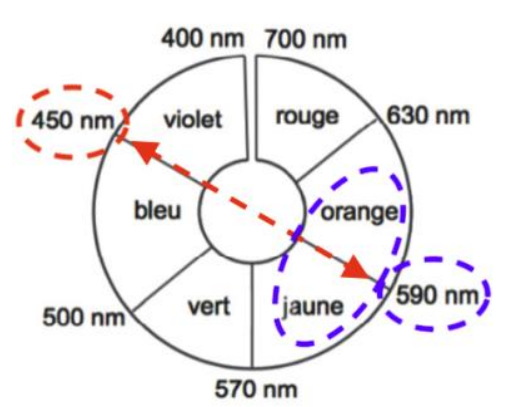
La couleur de la solution est la couleur complémentaire (couleur diamétralement opposée sur le cercle chromatique) : le jaune-orange
D’où la couleur de la solution aqueuse de diiode est de couleur jaune-brun.
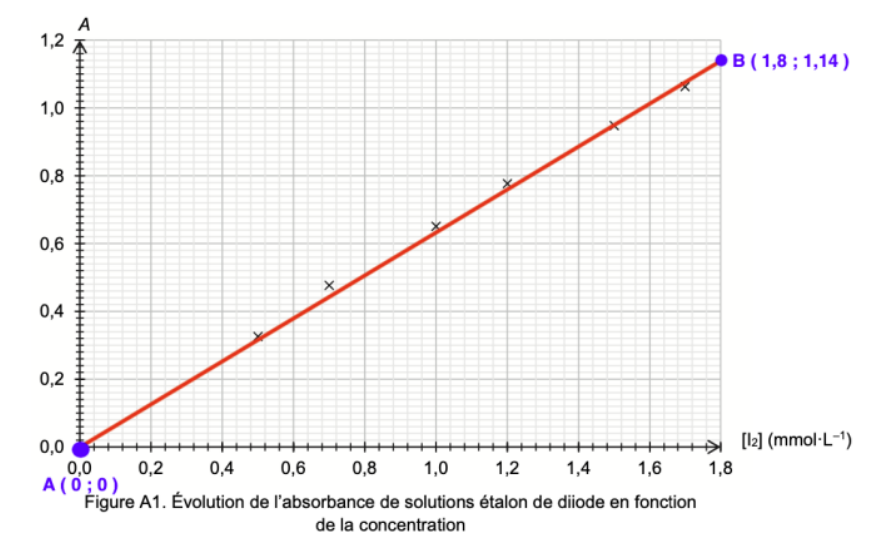
Q9. En utilisant et en complétant la figure A1 de l’ANNEXE 1 À RENDRE AVEC LA COPIE, montrer que nf(I2) dans la solution S1 est de l’ordre de 7×10–4 mol.
L’absorbance mesurée est : $A = 0,619$
Méthode 1 :
Graphiquement :$\ \left[I_2\right]_2=0,98\ mmol{.L}^{-1}$
Méthode 2 :
Trouvons le coefficient directeur K
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{1,14-0}{1,80-0}$
$k=0,63\ L.{\rm mmol}^{-1}$
$A=0,63\ \left[I_2\right]$
$0,63\ \left[I_2\right]=A$
$\left[I_2\right]=\frac{0,619\ }{0,63}$
$\left[I_2\right]_2=0,98\ mmol{.L}^{-1}$
Or la solution S1 est diluée d’un facteur 10 pour obtenir la solution S2.
$\left[I_2\right]_1=10\times\left[I_2\right]_2$
$\left[I_2\right]_1=10\times0,98$
$\left[I_2\right]_1=9,8\ mmol{.L}^{-1}\ $
$\left[I_2\right]_1=\frac{n_f\left(I_2\right)}{V_1}$
$\frac{n_f\left(I_2\right)}{V_1}=\left[I_2\right]_1$
$n_f\left(I_2\right)=\left[I_2\right]_1\times V_1$
$n_f\left(I_2\right)=9,8\times{10}^{-3}\ \times75\times{10}^{-3}$
$n_f\left(I_2\right)=7,4\times{10}^{-4}\ mol\ $
Ainsi, nf(I2) dans la solution S1 est de l’ordre de $7\times10^{-4}\ mol$.
Q10. Déterminer alors la concentration en masse de glucose contenu dans le jus de pomme étudié.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
$C_m=\frac{m_{glucose}}{V}$
Or
$n_0\left(C_6H_{12}O_6\right)=\frac{m_{glucose}}{M\left(C_6H_{12}O_6\right)}$
$\frac{m_{glucose}}{M\left(C_6H_{12}O_6\right)}=n_0\left(C_6H_{12}O_6\right)$
$m_{glucose}=n_0\left(C_6H_{12}O_6\right)\times M\left(C_6H_{12}O_6\right)$
donc
$C_{m,0}=\frac{n_0\left(C_6H_{12}O_6\right)\times M\left(C_6H_{12}O_6\right)}{V}$
Or
$n_0\left(C_6H_{12}O_6\right)=n_0\left(I_2\right)-n_f\left(I_2\right)$ (Q7.)
$C_{m,0}=\frac{\left(n_0\left(I_2\right)-n_f\left(I_2\right)\right)\times M\left(C_6H_{12}O_6\right)}{V}$
$C_{m,0}=\frac{\left(1,0\times{10}^{-3}\ -7,4\times{10}^{-4}\right)\times180,2\ }{10,0\times{10}^{-3}}$
$C_{m,0}=4,7\ g.L^{-1}$
C’est la concentration en masse de glucose dans la solution nommée S0.
Rappel du sujet : « introduire 10,0 mL de jus de pomme dans une fiole jaugée de 50 mL, puis compléter avec de l’eau distillée jusqu’au trait de jauge. On obtient la solution nommée S0. »
Le facteur de dilution est :
$F=\frac{V_{fille}}{V_{mere}}=\frac{50,0}{10,0}=5$
Il nous faut trouver la concentration en masse de glucose contenu dans le jus de pomme étudié.
$C_m=5\times C_{m,0}$
$C_m=5\times4,7$
$C_m=24\ g.L^{-1}$
3. Perception en bouche d’un jus de pomme
En plus du glucose, le saccharose est un autre sucre présent dans le jus de pomme ; il contribue également à la perception du goût sucré. La teneur en saccharose est évaluée en degré Brix (°B) : un degré Brix équivaut à 1 g de saccharose dans 100 g de solution.
Pour évaluer la perception en bouche d’un jus de pomme, un des critères utilisés par les industriels est le rapport R, sans dimension, entre sa teneur en saccharose évaluée en degré Brix et son titre massique d’acide malique, noté tm. Pour la majorité des consommateurs, on considère que l’équilibre entre les saveurs acides et sucrées est satisfaisant si ce rapport R est compris entre 30 et 40.
Données :
- $R = \frac{{°B}}{t_m}$ avec °B le degré Brix et tm le titre massique en acide malique exprimé en pourcentage.
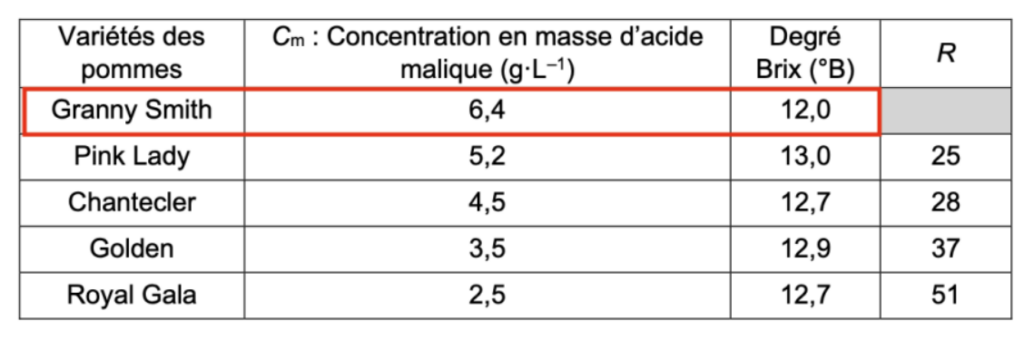
- résultats obtenus pour des jus de plusieurs variétés de pomme :
| Variétés des pommes | Cm : Concentration en masse d’acide malique (g·L–1) | Degré Brix (°B) | R |
| Granny Smith | 6,4 | 12,0 | |
| Pink Lady | 5,2 | 13,0 | 25 |
| Chantecler | 4,5 | 12,7 | 28 |
| Golden | 3,5 | 12,9 | 37 |
| Royal Gala | 2,5 | 12,7 | 51 |
Q11. Déterminer, en pourcentage, le titre massique tm d’acide malique dans le jus de pomme Granny Smith sachant que la masse volumique de ce jus de pomme est de 1,04 x103 g·L–1. Vérifier que le rapport R pour ce jus de pomme est inférieur à 25.
$t_m=\frac{m_{acide}}{m_{solution}}\times100$
Or
$C_m=\frac{m_{acide}}{V}$
$\frac{m_{acide}}{V}=C_m$
$m_{acide}=C_m\times V$
Or
$\rho=\frac{m_{solution}}{V}$
$\frac{m_{solution}}{V}=\rho$
$m_{solution}=\rho\times V$
D’où
$t_m=\frac{m_{acide}}{m_{solution}}\times100$
$t_m=\frac{C_m\times V}{\rho\times V}\times100$
$t_m=\frac{C_m}{\rho}\times100$
$t_m=\frac{6,4}{1,04\times{10}^3}\times100$
$t_m=0,62$
$R=°Btm$
$R=\frac{12,0}{0,62}$
$R=19$
Le rapport R pour ce jus de pomme est bien inférieur à 25.
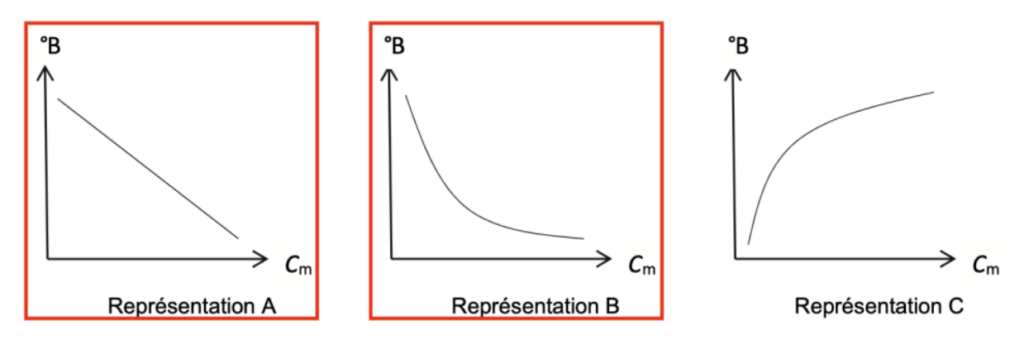
Q12. Choisir en justifiant, parmi les trois représentations graphiques A, B et C ci-dessous de °B = f(Cm), celle(s) qui pourrai(en)t traduire l’affirmation indiquée en début d’exercice : « Lors de leur dégustation, certaines semblent plus acides que d’autres, entraînant une sensation moins sucrée en bouche. »
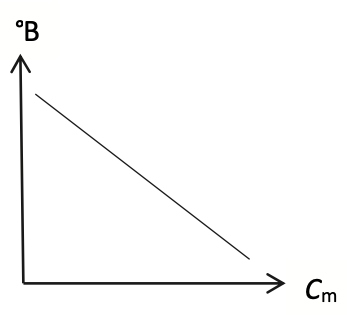
Représentation A
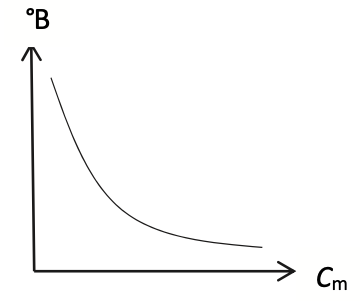
Représentation B
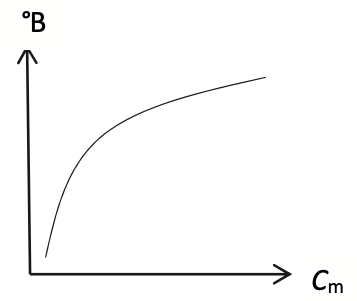
Représentation C
« Lors de leur dégustation, certaines semblent plus acides que d’autres, entrainant une sensation moins sucrée en bouche. »
Certaines semblent plus acides que d’autres : Cm augmente
Entrainant une sensation moins sucrée en bouche : La teneur en saccharose est évaluée en degré Brix (°B) diminue.
Celle(s) qui pourrai(en)t traduire l’affirmation indiquée en début d’exercice : doivent montrer que lorsque Cm augmente °B diminue : A et B.
Les résultats du tableau des analyses de différentes variétés de pomme sont reportés sur le graphe de la figure A2 de l’ANNEXE 1 À RENDRE AVEC LA COPIE.
Q13. Entourer sur le graphe de la figure A2 de l’ANNEXE 1 À RENDRE AVEC LA COPIE la mesure correspondant à la variété « Granny Smith ».
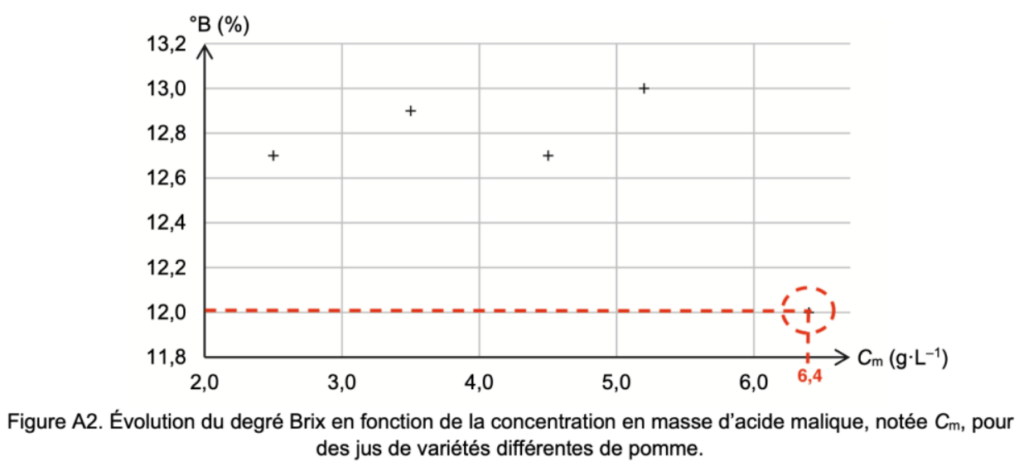
Q14. Commenter ce graphique au regard de l’existence potentielle d’un lien entre les teneurs °B et Cm étudiées et l’impression gustative laissée en bouche.
Ce graphique montre qu’il n’y a pas de lien potentiel entre les teneurs °B et Cm étudiées et l’impression gustative laissée en bouche.
ANNEXE 1 À RENDRE AVEC LA COPIE
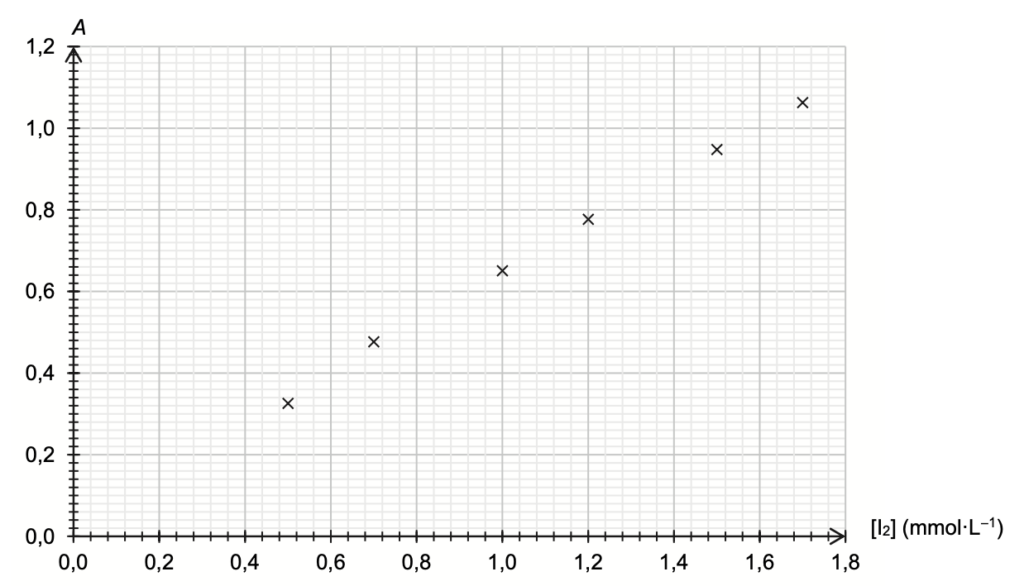
Figure A1. Évolution de l’absorbance de solutions étalon de diiode en fonction de la concentration
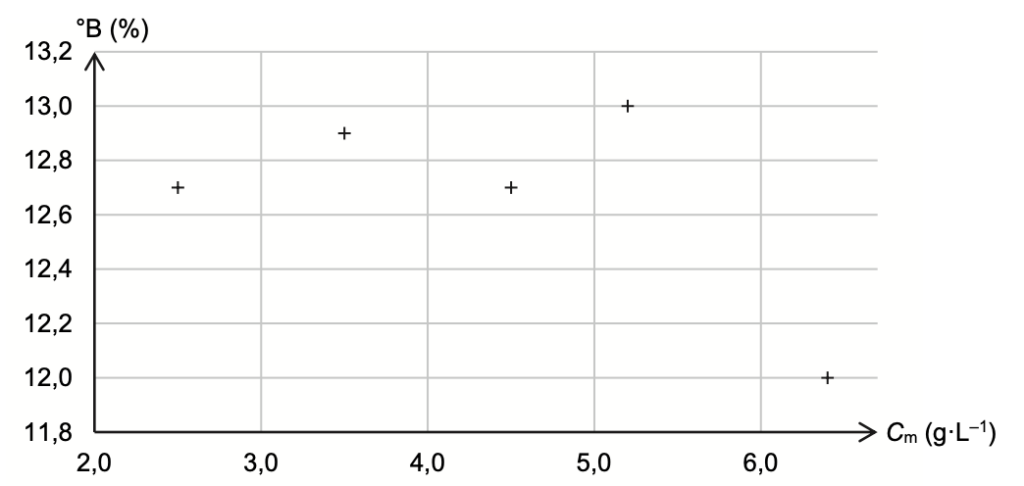
Figure A2. Évolution du degré Brix en fonction de la concentration en masse d’acide malique, notée Cm, pour des jus de variétés différentes de pomme.
