Métropole Septembre 2022 Sujet 1
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n° 22-PYCJ1ME3
Sujet et corrigé
L’acide méthanoïque, ou acide formique, est produit par des fourmis rouges qui l’utilisent pour se défendre. Il est synthétisé dans l’industrie pour être utilisé dans de nombreux domaines comme le textile, l’agroalimentaire, ou encore la fabrication de solvants.
Les objectifs de cet exercice sont d’étudier les propriétés acido-basiques de l’acide méthanoïque puis son utilisation dans la synthèse du méthanoate d’éthyle qui est un solvant organique.
Données :
- couple acide-base acide méthanoïque / ion méthanoate : HCOOH(aq) / HCOO–(aq) ;
- table de données de bandes d’absorption en spectroscopie infra-rouge (IR) :
| Liaison | C=O | O-H (acide carboxylique) | C-H |
| Nombre d’onde (cm–1) | 1700 – 1800 | 2500 – 3200 | 2800 – 3000 |
| Allure de la bande | Forte et mince | Forte et large | Forte et mince |
- propriétés physico-chimiques de différentes espèces chimiques :
| Espèce | Acide méthanoïque | Éthanol | Méthanoate d’éthyle | Eau |
| Formule brute | CH2O2 | C2H6O | C3H6O2 | H2O |
| Masse molaire moléculaire | 46,0 g·mol–1 | 46,1 g·mol–1 | 74,1 g·mol–1 | 18,0 g·mol–1 |
| Température d’ébullition | 101 °C | 79 °C | 54 °C | 100 °C |
- sur l’étiquette du flacon de l’acide méthanoïque concentré commercial utilisé, on lit que le titre massique minimum est de 85 %. La densité mesurée de ce produit est mesurée, elle vaut 1,19.
1. Propriétés acido-basiques de l’acide méthanoïque
Pour étudier les propriétés acido-basiques de l’acide méthanoïque, une solution aqueuse d’acide méthanoïque, notée S, est préparée à partir de 1,0 mL d’acide méthanoïque concentré commercial dilué dans une fiole jaugée de 250 mL.
Le titrage d’un volume V = 25,0 mL de solution S est réalisé et suivi par pH-métrie. La solution titrante est une solution aqueuse d’hydroxyde de sodium de concentration cB égale à 0,20 mol·L–1. La courbe du suivi pH- métrique est donnée en figure 1.
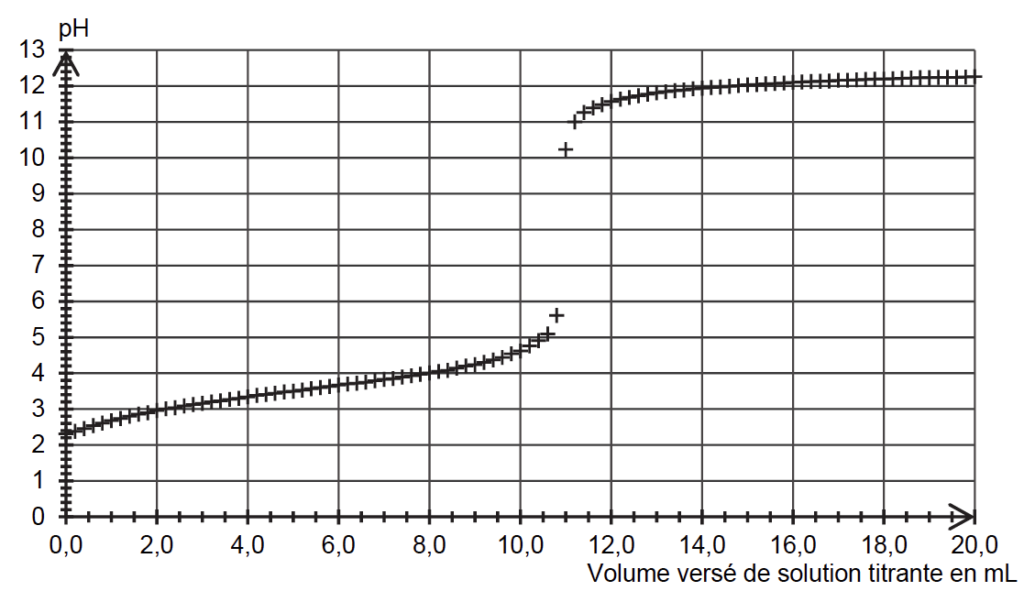
Q1. Écrire l’équation de la réaction support du titrage.
Acide méthanoïque $HCOOH$
Hydroxyde de sodium $\left({\rm Na}^+ + {\rm HO}^-\right)$
Équation de la réaction support du titrage :
$$HCOOH_{(aq)} + {\rm HO}_{(aq)}^- \rightarrow {\rm HCOO}_{(aq)}^- + H_2O_{(l)}$$
Q2. Déterminer la valeur de la concentration en quantité de matière d’acide méthanoïque présent dans la solution S.
L’équivalence correspond au mélange stœchiométrique des réactifs pour la réaction mis en jeu. A l’équivalence, il y a changement du réactif limitant.
Veq trouvé à l’aide de la méthode des tangentes parallèles : Veq =11,0 mL
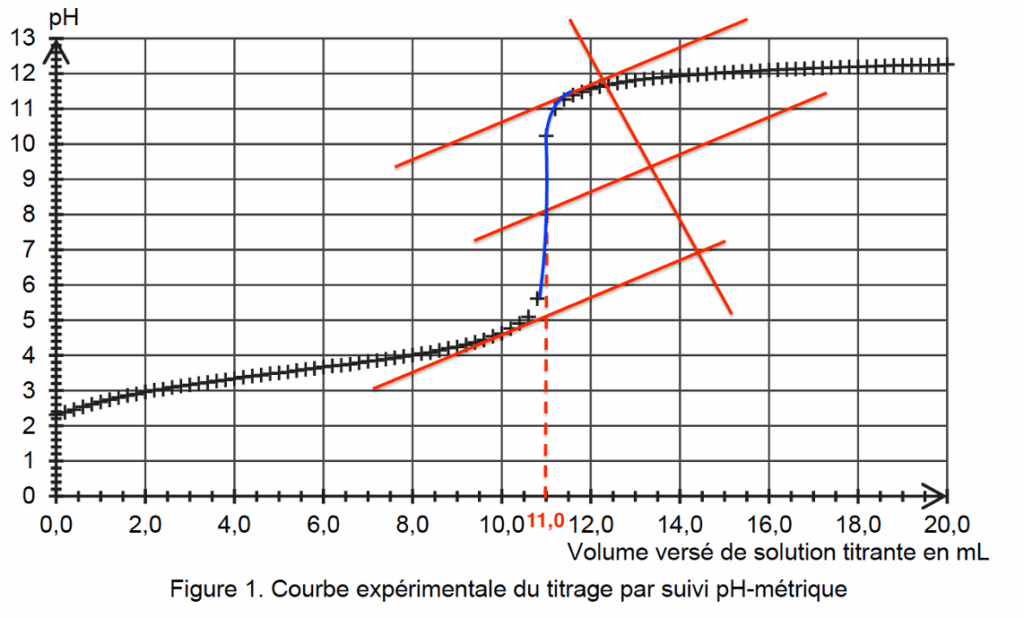
À l’équivalence :
$$\frac{n_{HCOOH}^i}{1} = \frac{n_{{\rm HO}^-}^{eq}}{1}$$
$$c_S \times V = c_B \times V_{eq}$$
$$c_S = \frac{c_B \times V_{eq}}{V}$$
$$c_S = \frac{0,20 \times 11,0 \times 10^{-3}}{25,0 \times 10^{-3}}$$
$$c_S = 8,8 \times 10^{-2}\ {\rm mol.L^{-1}}$$
Q3. En déduire la valeur du titre massique d’acide méthanoïque de la bouteille utilisée. Commenter.
D’après l’énoncé : S est préparée à partir de 1,0 mL d’acide méthanoïque concentré commercial dilué dans une fiole jaugée de 250 mL.
C’est une dilution :
$$n = n_S$$
$$c \times V = c_S \times V_S$$
$$c = \frac{c_S \times V_S}{V}$$
$$c = \frac{8,8 \times 10^{-2} \times 250 \times 10^{-3}}{1,0 \times 10^{-3}}$$
$$c = 22\ {\rm mol.L^{-1}}$$
Le titre massique ou pourcentage massique est défini par :
$$w = \frac{m_{soluté}}{m_{solution}}$$
Or
$$n_{soluté} = \frac{m_{soluté}}{M}$$
$$m_{soluté} = n_{soluté} \times M$$
D’où
$$w = \frac{n_{soluté} \times M}{m_{solution}}$$
Or
$$\rho_{solution} = \frac{m_{solution}}{V_{solution}}$$
$$m_{solution} = \rho_{solution} \times V_{solution}$$
D’où
$$w = \frac{n_{soluté} \times M}{\rho_{solution} \times V_{solution}}$$
Or
$$c = \frac{n_{soluté}}{V_{solution}}$$
$$n_{soluté} = c \times V_{solution}$$
D’où
$$w = \frac{c \times V_{solution} \times M}{\rho_{solution} \times V_{solution}}$$
$$w = \frac{c \times M}{\rho_{solution}}$$
Or
$$d = \frac{\rho_{solution}}{\rho_{eau}}$$
$$\rho_{solution} = d \times \rho_{eau}$$
D’où
$$w = \frac{c \times M}{d \times \rho_{eau}}$$
$$w = \frac{22 \times 46,0}{1,19 \times 1000}$$
$$w = 0,85$$
$$w = 85\ %$$
D’après l’énoncé : sur l’étiquette du flacon de l’acide méthanoïque concentré commercial utilisé, on lit que le titre massique minimum est de $85\ %$.
Le titre massique d’acide méthanoïque mesuré est en accord avec la mention de l’étiquette.
On utilise les valeurs de pH mesurées au cours de ce titrage pour déterminer si l’acide méthanoïque peut être considéré comme un acide fort ou un acide faible. L’exploitation des mesures de pH permet d’obtenir la figure 2.
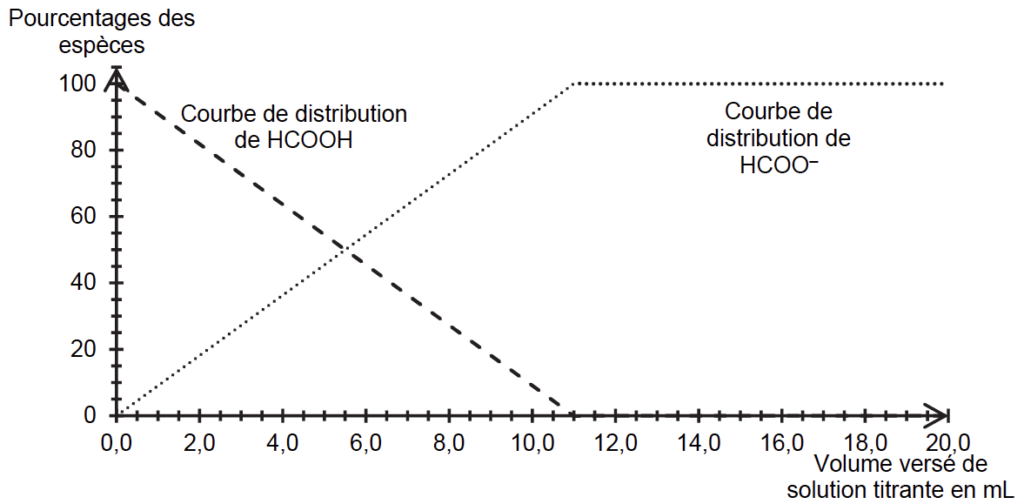
Figure 2. Courbes de distribution obtenues à partir des mesures de pH effectuées lors du titrage
Q4. Écrire l’équation de la réaction dont la constante thermodynamique d’équilibre correspond à la constante d’acidité KA du couple acide méthanoïque / ion méthanoate.
Équation de la réaction dont la constante thermodynamique d’équilibre correspond à la constante d’acidité KA du couple acide méthanoïque / ion méthanoate :
$$HCOOH_{(aq)} + H_2O_{(l)} \rightleftarrows {\rm HCOO}_{(aq)}^- + {H_3O}_{(aq)}^+$$
Q5. Estimer, en expliquant la démarche, à l’aide des figures 1 et 2, la valeur de la constante d’acidité KA du couple acide méthanoïque / ion méthanoate à la température du titrage.
$$K_A = \frac{\left[{\rm HCOO}^-\right]_{eq} \times \left[H_3O^+\right]_{eq}}{\left[HCOOH\right]_{eq} \times c^0}$$
$$pK_A = -\log(K_A)$$
$$pK_A = -\log\left(\frac{\left[{\rm HCOO}^-\right]_{eq} \times \left[H_3O^+\right]_{eq}}{\left[HCOOH\right]_{eq} \times c^0}\right)$$
$$pK_A = -\log\left(\frac{\left[{\rm HCOO}^-\right]_{eq}}{\left[HCOOH\right]_{eq}}\right) – \log\left(\frac{\left[H_3O^+\right]_{eq}}{c^0}\right)$$
$$pK_A = -\log\left(\frac{\left[{\rm HCOO}^-\right]_{eq}}{\left[HCOOH\right]_{eq}}\right) + pH$$
Donc
$$pH = pK_A + \log\left(\frac{\left[{\rm HCOO}^-\right]_{eq}}{\left[HCOOH\right]_{eq}}\right)$$
Lorsque $\left[{\rm HCOO}^-\right]_{eq} = \left[HCOOH\right]_{eq}$ alors $pH = pK_A$.
D’après la figure 2, $\left[{\rm HCOO}^-\right]_{eq} = \left[HCOOH\right]_{eq}$ pour un volume versé de solution titrante $V = 5,5\ {\rm mL}$.
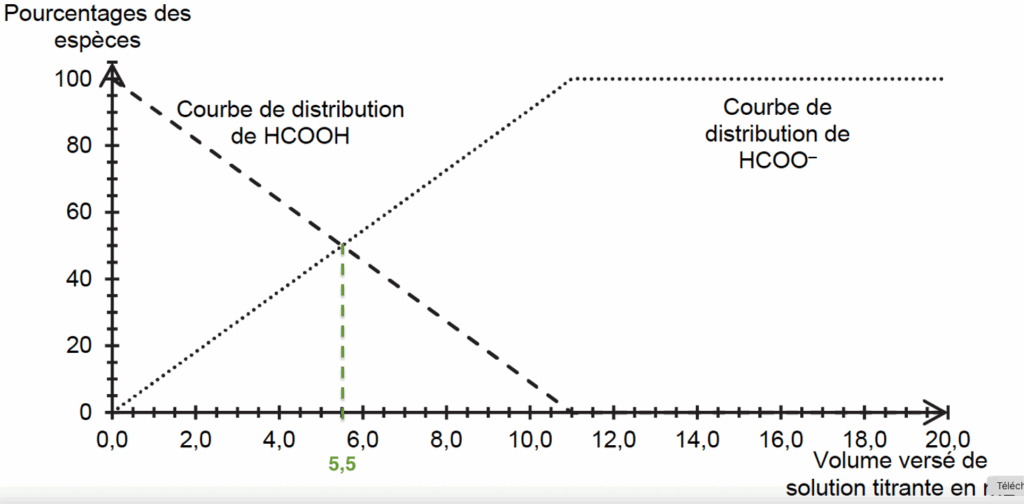
D’après la figure 1 pour un volume versé de solution titrante V= 5,0 mL : pH=3,6
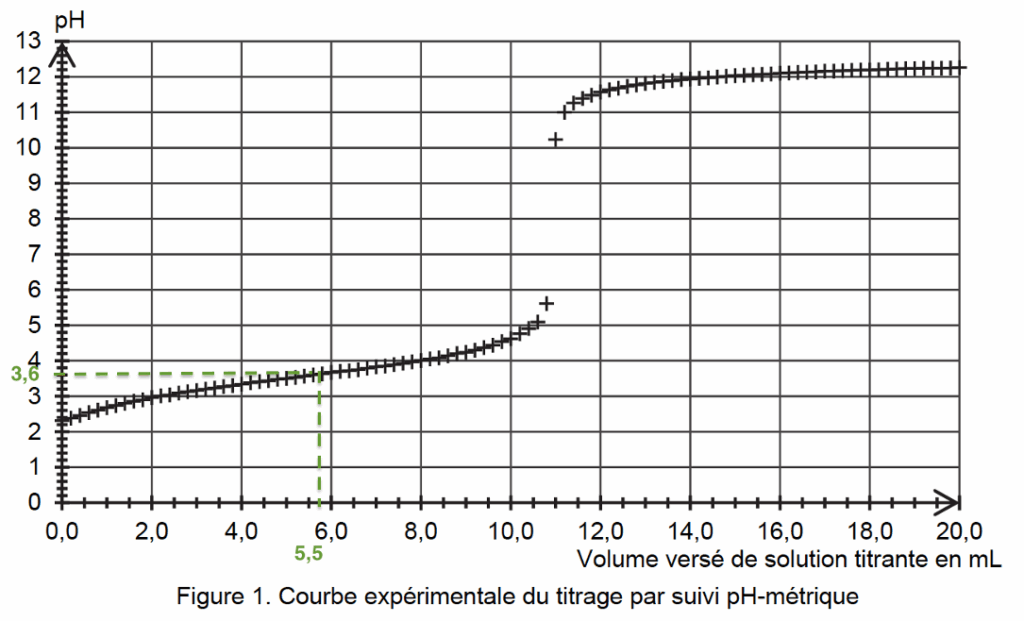
Donc $pK_A = 3,6$
$$K_A = 10^{-pK_A}$$
$$K_A = 10^{-3,6}$$
$$K_A = 2,5 \times 10^{-4}$$
La valeur tabulée de la constante d’acidité associée à ce couple est égale à 1,75×10-4 à 25 °C.
Q6. Identifier une des causes expliquant l’écart entre la valeur tabulée et la valeur calculée à la question Q5 de la constante d’acidité KA du couple acide méthanoïque / ion méthanoate.
La valeur tabulée de la constante d’acidité associée à ce couple est égale à 1,75×10-4 à 25 °C.
Cette valeur est donnée pour une température de 25 °C. Or la température n’est pas mesurée dans notre cas.
Une température différente peut être l’une des causes expliquant l’écart entre la valeur tabulée et la valeur calculée à la question Q5
On étudie une solution aqueuse d’acide méthanoïque de concentration initiale en soluté apportée cA.
Q7. Montrer que le quotient de réaction, noté Qr, associé à la réaction écrite à la question Q4, s’écrit :
$Q_r=\frac{[H_3O^+]^2}{(C_A-[H_3O^+])C^0}$
avec c° la concentration standard.
| $$HCOOH_{(aq)}$$ | $$+ H_2O_{(l)}$$ | $$\rightleftarrows {\rm HCOO}_{(aq)}^-$$ | $$+ {H_3O}_{(aq)}^+$$ | |
| État initial | cAV | Solvant | 0 | 0 |
| État intermédiaire | cAV-x | Solvant | x | x |
| État final | cAV-xeq | Solvant | xeq | xeq |
$$[{\rm HCOO}^-] = \frac{x}{V}$$
$$[H_3O^+] = \frac{x}{V}$$
$$[HCOOH] = c_A – \frac{x}{V}$$
Ainsi :
$$[{\rm HCOO}^-] = [H_3O^+]$$
$$[HCOOH] = c_A – [H_3O^+]$$
$$Q_r = \frac{[{\rm HCOO}^-] \times [H_3O^+]}{[HCOOH] \times c^0}$$
$$Q_r = \frac{[H_3O^+]^2}{(c_A – [H_3O^+]) \times c^0}$$
Q8. Montrer que l’on peut estimer la valeur de KA à une température donnée avec la relation suivante :
$K_A=\frac{\tau_f^2C_A}{(1-\tau_f)C^0}$
avec τf le taux d’avancement final.
$$K_A = Q_{r,eq}$$
$$K_A = \frac{[H_3O^+]_{eq}^2}{(c_A – [H_3O^+]_{eq}) \times c^0}$$
$$c_A V – x_{max} = 0$$
$$x_{max} = c_A V$$
$$x_{eq} = n_{H_3O^+}^{eq}$$
$$x_{eq} = [H_3O^+]_{eq} \times V$$
$$\tau_f = \frac{x_{eq}}{x_{max}}$$
$$\tau_f = \frac{[H_3O^+]_{eq} \times V}{c_A V}$$
$$\tau_f = \frac{[H_3O^+]_{eq}}{c_A}$$
$$[H_3O^+]_{eq} = \tau_f \times c_A$$
D’où
$$K_A = \frac{[H_3O^+]_{eq}^2}{(c_A – [H_3O^+]_{eq}) \times c^0}$$
$$K_A = \frac{(\tau_f \times c_A)^2}{(c_A – \tau_f \times c_A) \times c^0}$$
$$K_A = \frac{\tau_f^2 \times c_A^2}{c_A \times (1 – \tau_f) \times c^0}$$
$$K_A = \frac{\tau_f^2 \times c_A}{(1 – \tau_f) \times c^0}$$
Le taux d’avancement τf vérifie une équation du 2nd degré de la forme :
A · τf2 + B · τf + C = 0 avec A, B et C des constantes.
Le calcul du taux d’avancement est effectué à l’aide d’un programme écrit en langage Python dont un extrait est donné en figure 3.
| 4 | # Demandes des valeurs utiles |
| 5 | cA=float(input(« Indiquer la concentration apportée cA (en mol/L) de l’acide : »)) |
| 6 | KA=float(input(« Indiquer la valeur de la constante d’acidité KA : »)) |
| 7 | c0 = 1.0 # valeur de la concentration standard en mol/L |
| 8 | |
| 9 | # Equation du 2nd degré vérifiée par le taux d’avancement |
| 10 | # équation du type : A*tau^2 + B*tau + C = 0 |
| 11 | A = ? # expression de A |
| 12 | B = ? # expression de B |
| 13 | C = ? # expression de C |
Figure 3. Extrait du programme écrit en langage Python
Q9. Compléter les lignes 11, 12 et 13 permettant au programme d’être exécuté. Détailler la démarche.
D’après l’énoncé : le taux d’avancement $\tau_f$ vérifie une équation du second degré de la forme :
$$(A \times \tau_f)^2 + B \times \tau_f + C = 0$$
Mettons l’équation trouvée à la question 8 sous cette forme :
$$K_A = \frac{\tau_f^2 \times c_A}{(1 – \tau_f) \times c^0}$$
$$K_A \times (1 – \tau_f) \times c^0 = \tau_f^2 \times c_A$$
$$\tau_f^2 \times c_A – K_A \times (1 – \tau_f) \times c^0 = 0$$
$$c_A \times \tau_f^2 + K_A \times c^0 \times \tau_f – K_A \times c^0 = 0$$
Par identification :
$A = c_A$
$B = K_A \times c^0$
$C = -K_A \times c^0$
Ainsi nous pouvons compléter les lignes 11, 12 et 13 permettant au programme d’être exécuté :
Ligne 11 : $A = c_A$
Ligne 12 : $B = K_A \times c^0$
Ligne 13 : $C = -K_A \times c^0$
Pour une solution aqueuse d’acide méthanoïque de concentration apportée égale à 8,8×10-2 mol·L–1, le résultat obtenu par le programme est donné ci-dessous :
Indiquer la concentration apportée cA (en mol/L) de l’acide :0.088
Indiquer la valeur de la constante d’acidité KA :1.75e-4
Il y a 2 solutions possibles pour le taux d’avancement final :
tau1 = -0.046
tau2 = 0.044
Q10. À partir des résultats ci-dessus du programme, déterminer en justifiant si l’acide méthanoïque peut être considéré comme un acide fort ou un acide faible dans l’eau dans les conditions de l’expérience.
Il y a deux solutions possibles pour le taux d’avancement final :
$\tau_1 = -0,046$
$\tau_2 = 0,044$
Nous ne gardons que la valeur positive de $\tau$ :
$\tau = \tau_2 = 0,044$
Le taux d’avancement est inférieur à 1, la réaction est limitée : l’acide méthanoïque peut être considéré comme un acide faible dans l’eau dans les conditions de l’expérience.
2. Synthèse du méthanoate d’éthyle à partir d’acide méthanoïque
Le méthanoate d’éthyle peut être utilisé, par exemple, comme solvant organique, mais également pour donner une odeur de rhum à un aliment.
La synthèse du méthanoate d’éthyle se fait à partir d’acide méthanoïque et d’éthanol. L’équation de la réaction modélisant cette transformation chimique peut s’écrire :

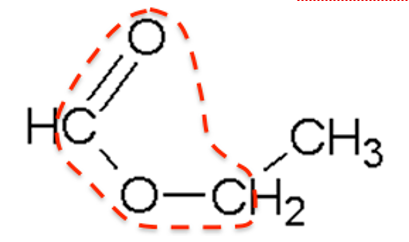
Q11. Écrire sur votre copie la formule semi-développée du méthanoate d’éthyle, entourer le groupe caractéristique et nommer la famille fonctionnelle associée.
Formule semi-développée du méthanoate d’éthyle :
Famille fonctionnelle : ester
Q12. Les spectres IR de l’acide méthanoïque et du méthanoate d’éthyle sont donnés en figure 4. Attribuer, en justifiant, chaque spectre à l’espèce chimique correspondante.
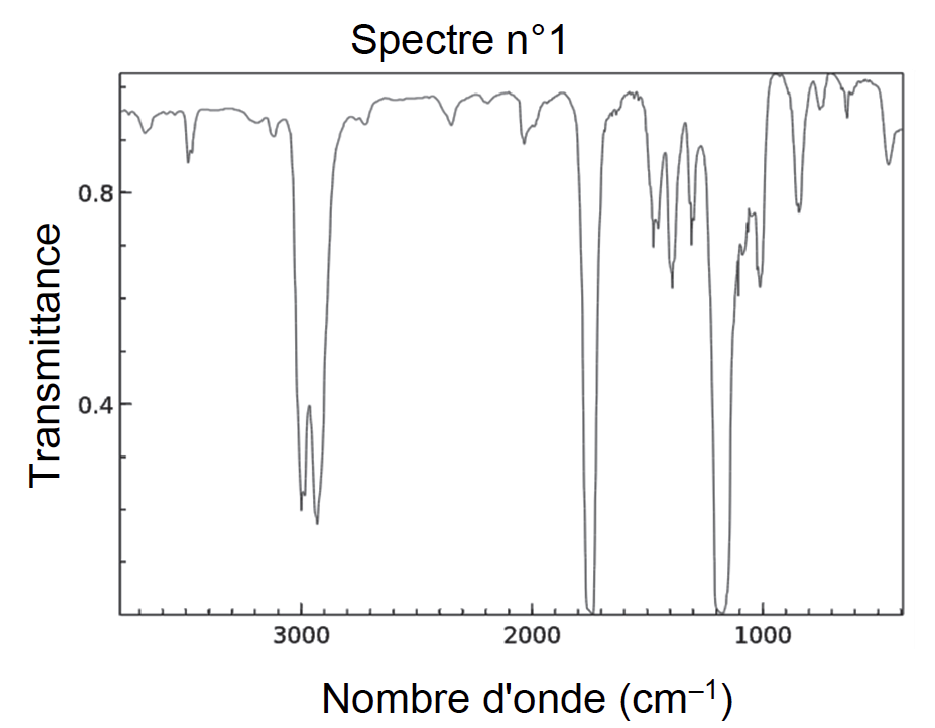
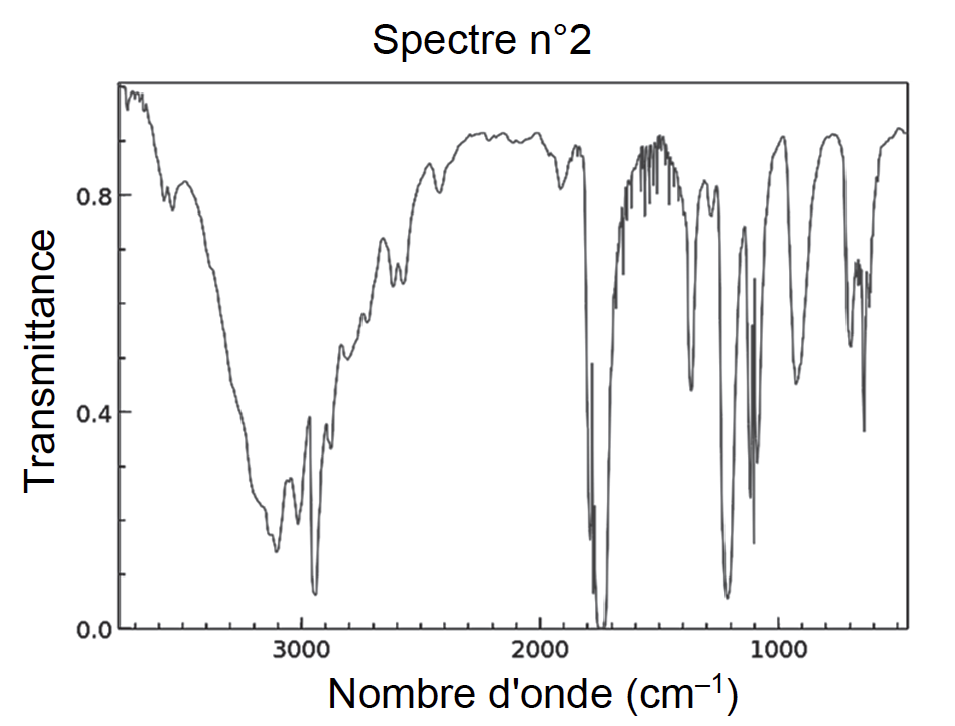
Figure 4. Spectres Infra-Rouge (IR) de deux molécules
Liaison dans l’acide méthanoïque :
- C=O. Nombre d’onde 1700 – 1800 cm−1
- O−H (acide carboxylique). Nombre d’onde 2500 – 3200 cm−1
- C−H. Nombre d’onde 2800 – 3000 cm−1
Liaison dans méthanoate d’éthyle :
- C=O. Nombre d’onde 1700 – 1800 cm−1
- C−H. Nombre d’onde 2800 – 3000 cm−1
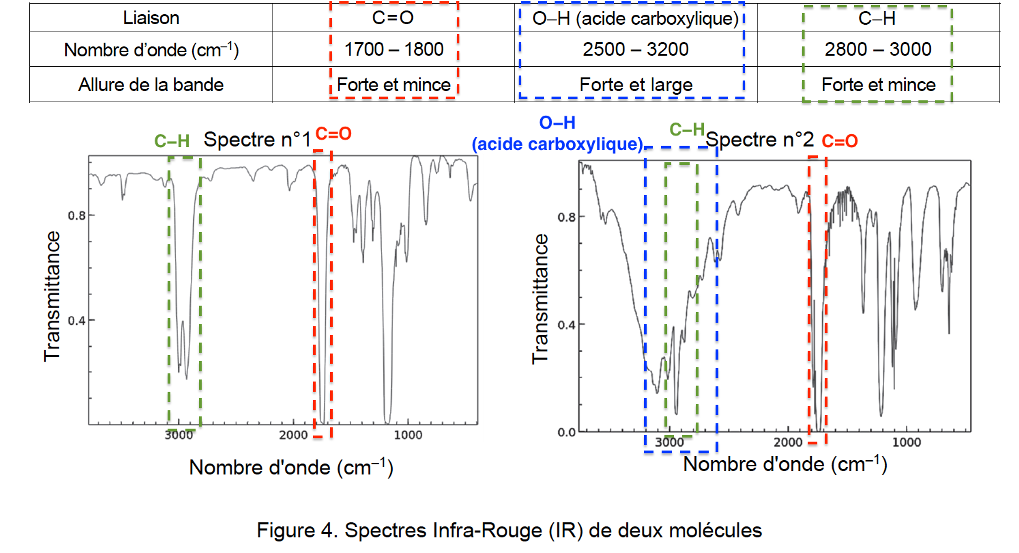
Le spectre IR n°1 est celui du méthanoate d’éthyle.
Le spectre IR n°2 est celui de l’acide méthanoïque.
On réalise la synthèse du méthanoate d’éthyle selon le protocole suivant :
- introduire dans un ballon 11,5 g d’éthanol, 11,5 g d’acide méthanoïque, 5 gouttes d’acide sulfurique concentré et quelques grains de pierre ponce ;
- chauffer à reflux durant 45 min ;
- laisser refroidir.
Q13. Citer un intérêt à l’utilisation d’un montage à reflux.
Un montage à reflux permet d’accélérer la réaction sans perte de matière.
Pour déterminer le rendement de la synthèse, on réalise un titrage de l’acide méthanoïque restant dans le milieu réactionnel à la fin de la synthèse. On en déduit que la valeur de la quantité de matière d’acide méthanoïque restante est égale à 0,13 mol.
Q14. Calculer le rendement de cette synthèse.
$n_{acide\ méthanoïque}^i = \frac{m_{acide\ méthanoïque}}{M_{acide\ méthanoïque}}$
$n_{acide\ méthanoïque}^i = \frac{11,5}{46,0}$
$n_{acide\ méthanoïque}^i = 0,25\ mol$
$n_{éthanol}^i = \frac{m_{éthanol}}{M_{éthanol}}$
$n_{éthanol}^i = \frac{11,5}{46,1}$
$n_{éthanol}^i = 0,25\ mol$

| Équation | |||||
| État initial | x=0mol | 0,25 | 0,25 | 0 | 0 |
| État intermédiaire | x | 0,25–x | 0,25–x | x | x |
| État final | x=xf | 0,25–xf | 0,25–xf | xf | xf |
Calculons $x_{max}$ :
$0,25 – x_{max} = 0$
$x_{max} = 0,25\ mol$
D’après le texte : la valeur de la quantité de matière d’acide méthanoïque restante est égale à $0,13\ mol$.
Calculons $x_f$ :
$0,25 – x_f = 0,13$
$-x_f = 0,13 – 0,25$
$-x_f = -0,12$
$x_f = 0,12\ mol$
Calculons le rendement :
$\eta = \frac{n_{exp}}{n_{Th}}$
$\eta = \frac{x_f}{x_{max}}$
$\eta = \frac{0,12}{0,25} = 0,48 = 48\ %$
Pour optimiser le rendement de la synthèse, on modifie certaines conditions expérimentales. Les différentes modifications sont présentées dans le tableau de la figure 5.
| Voie n° | Protocole | Rendement |
| 1 | À l’aide d’un montage à reflux, on fait réagir durant 45 minutes 0,50 mol d’éthanol, 0,25 mol d’acide méthanoïque, 5 gouttes d’acide sulfurique concentré et quelques grains de pierre ponce. | 67 % |
| 2 | À l’aide d’un montage à reflux, on fait réagir durant 45 minutes 1,0 mol d’éthanol, 0,25 mol d’acide méthanoïque, 5 gouttes d’acide sulfurique concentré et quelques grains de pierre ponce. | 76 % |
| 3 | À l’aide d’un montage de distillation fractionnée, on fait réagir durant 45 minutes 0,50 mol d’éthanol, 0,25 mol d’acide méthanoïque, 5 gouttes d’acide sulfurique concentré et quelques grains de pierre ponce. | 93 % |
Lors de la synthèse utilisant la voie n°3, le thermomètre au sommet de la colonne de distillation (colonne de Vigreux) indique une température de 54 °C.
Q15. À l’aide du tableau de la figure 5, identifier les conditions expérimentales mises en œuvre dans les protocoles qui permettent d’optimiser le rendement de la synthèse.
Le rendement de la synthèse est optimisé lorsqu’il est le plus grand. La voie 3 permet le plus grand rendement.

Les conditions expérimentales mises en œuvre dans les protocoles qui permettent d’optimiser le rendement de la synthèse sont :
- Montage de distillation fractionnée durant 45 minutes
- 0,50 mol d’éthanol
- 0,25 mol d’acide méthanoïque
- 5 gouttes d’acide sulfurique concentré
- Quelques grains de pierre ponce.
