Bac Centres étrangers 2021 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2G11
Sujet et corrigé
Mots-clés : couples acide-base, titrage avec suivi pH-métrique.
« L’ammoniaque » est une solution obtenue en dissolvant du gaz ammoniac, NH3(g), dans l’eau. Cette solution est présente dans de nombreux produits d’entretien.
On dispose d’une bouteille « d’ammoniaque » achetée dans le commerce dont l’étiquette précise : « Ammoniaque concentration 13% ».
« 13% » correspond au titre massique de la solution commerciale en ammoniac.

On souhaite mettre en œuvre un protocole permettant de déterminer la concentration en ammoniac dans la solution commerciale.
Données à 25°C :
- Masse molaire de l’ammoniac : M(NH3) = 17,0 g⋅mol−1
- Produit ionique de l’eau : Ke = 1,0 ⋅ 10−14
- Densité de la solution d’ammoniaque commerciale : d = 0,97
- pKa = − log Ka
- couple acide-base : NH4+(aq)/NH3(aq), pKa = 9,2
- NH4+ est la formule chimique de l’ion ammonium
Étude préliminaire : étude du couple ion ammonium/ammoniac
L’ammoniac est très soluble dans l’eau.
1. Préciser si l’ammoniac est un acide ou une base en solution aqueuse. Justifier.
L’ammoniac NH3 est une base car capable de capter un proton H+ :
$$NH_3+\ H^+={\rm NH}_4^+$$
2. Écrire l’équation de la réaction modélisant la transformation mise en jeu entre l’ammoniac dissous, NH3 (aq), et l’eau.
$$NH_{3(aq)}+\ H_2O_{(l)}={\rm NH}_{4(aq)}^++HO_{(aq)}^-$$
3. Donner la valeur de la constante d’acidité Ka 𝑎 du couple NH4+(aq)/NH3(aq).Rappeler la relation la liant, à l’équilibre, aux concentrations des espèces.
$$pK_A=-\log{\left(K_A\right)}$$
$$K_A={10}^{-pK_A}$$
$$K_A={10}^{-9,2}=6,3.{10}^{-10}$$
Relation la liant, à l’équilibre, aux concentrations des espèces :
$$K_A=\frac{\left[NH_3\right]_{eq} \times \left[H_30^+\right]_{eq}}{\left[{\rm NH}_4^+\right]_{eq}}$$
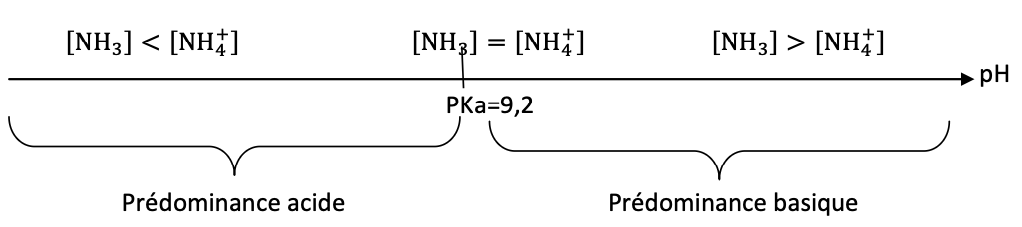
4. Tracer le diagramme de prédominance du couple NH4+(aq)/NH3(aq).
Diagramme de prédominance :
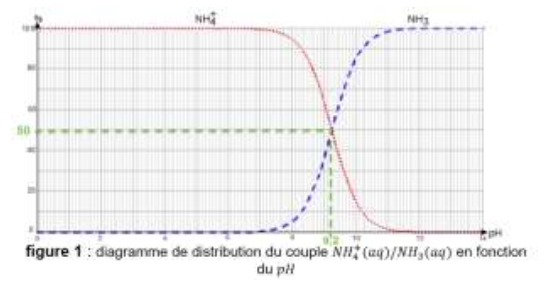
5. Expliquer comment retrouver le pKa du couple NH4+(aq)/NH3(aq) à partir du diagramme de distribution représenté en figure 1.
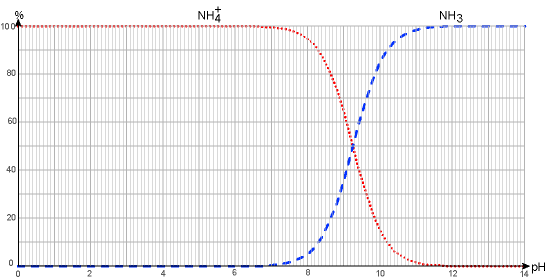
figure 1 : diagramme de distribution du couple NH4+(aq)/NH3(aq) en fonction du pH
Lorsque [NH3]=[NH4+] , pH= pKA
On lit sur la Figure 1 : [NH3]=[NH4+] pour pH=9,2
Donc pKA=9,2
Concentration attendue en ammoniac dans la solution commerciale
6. À partir de la donnée figurant sur l’étiquette, montrer que la concentration en quantité de matière de l’ammoniac dans la solution commerciale est de l’ordre de 7,4 mol. L−1.
$$c_A=\frac{n_A}{V_{sol}}$$
Or
$$n_A=\frac{m_A}{M_A}$$
$$ \Longrightarrow c_A=\frac{m_A}{M_A \times V_{sol}}$$
Or $$P_A=\frac{m_A}{m_{sol}} , m_A=P_A \times m_{sol} $$
$$\Longrightarrow c_A=\frac{P_A \times m_{sol}}{M_A \times V_{sol}}$$
Or $$\rho_{sol}=\frac{m_{sol}}{V_{sol}}$$
$$\Longrightarrow c_A=\frac{P_A \times \rho_{sol}}{M_A}$$
Or
$$d_{sol}=\frac{\rho_{sol}}{\rho_{eau}}$$
$$\rho_{sol}=d_{sol} \times \rho_{eau}$$
$$\Longrightarrow c_A=\frac{P_A \times d_{sol} \times \rho_{eau}}{M_A}$$
$$c_A=\frac{0,13 \times 0,97 \times 1000}{17}=7,4\ mol.L^{-1} $$
Titrage de la solution « d’ammoniaque » commerciale
La solution S0 de la bouteille « d’ammoniaque » étant trop concentrée pour réaliser le titrage, une solution Sd, 100 fois moins concentrée est préparée et on réalise un titrage suivi par
pH-métrie de cette solution diluée.
- On prélève un volume Vd = 10,0 mL de solution Sd.
- On titre ce prélèvement par une solution d’acide chlorhydrique (H3O+(aq), Cl−(aq)) de concentration CA = (5,00 ± 0,02) × 10−2 mol⋅L−1.
Les résultats des mesures effectuées au cours du titrage et leur exploitation sont présentés dans la figure 2.
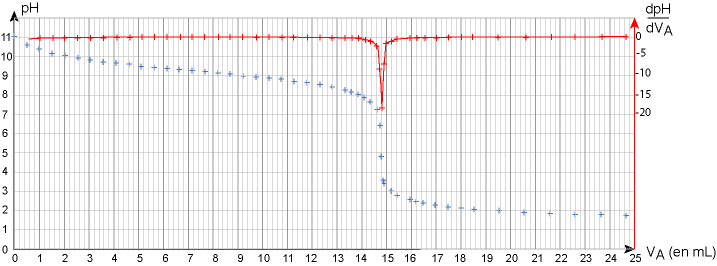
figure 2 : évolution du pHet de sa dérivée en fonction de VA
7. À partir des résultats expérimentaux,
– déterminer la valeur du pH de la solution Sd ;
– déterminer l’espèce de couple ammonium/ammoniac prédominante au début du titrage, et celle prédominante à la fin du titrage ;
– en déduire que l’équation de la réaction acide-base support du titrage est la suivante :
NH3(aq) + H3O+(aq) → NH4+(aq) + H2O(ℓ)
pH de la solution Sd : lorsque VA=0mL , la réaction n’a pas commencée , le pH est celui de la solution Sd . Par lecture graphique pH=11
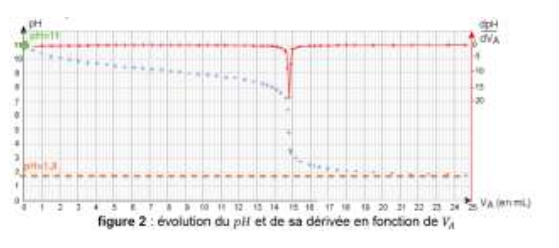
- Détermination l’espèce de couple ammonium/ammoniac prédominante au début du titrage, et celle prédominante à la fin du titrage
En début de titrage, pH=11 , prédominant au début du titrage (Diagramme de prédominance de la question 4).
A la fin du titrage, pH=1,8 (lecture graphique figure 2),
prédominant (Diagramme de prédominance de la question 4).

Équation de la réaction acide-base support du titrage
D’après le sujet « on titre ce prélèvement par une solution d’acide chlorhydrique (H3O+ (aq), Cl-(aq)) »
Les espèces $NH_3$ et $H_30^+$ sont présentes au début du titrage , elles réagissent ensemble pour former ${\rm NH}_4^+$ (présent en fin de titrage) : $$NH_{3(aq)}+H_3O_{(aq)}^+\rlhar{\rm NH}_{4(aq)}^++H_2O_{(l)}$$
8. Définir l’équivalence du titrage et déterminer le volume équivalent 𝑉𝐸 de ce titrage.
L’équivalence correspond au mélange stœchiométrique des réactifs pour la réaction mis en jeu. A l’équivalence, il y a changement du réactif limitant.
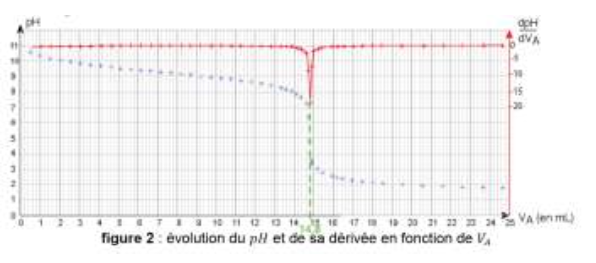
Veq trouvé au pic de la courbe $\frac{dpH}{dV_A}$
Veq =14,8 mL
9. Déterminer la valeur de la concentration Cd en ammoniac dans la solution Sd.
A l’équivalence :
$$\frac{n_{NH_3}^i}{1}=\frac{n_{H_30^+}^{eq}}{1}$$
$$c_d \times V_d=c_A \times V_{eq}$$
$$c_d=\frac{c_A \times V_{eq}}{V_d}$$
$$c_d=\frac{5,00.{10}^{-2} \times 14,8}{10,0}$$
$$c_d=7,40.{10}^{-2}mol.L^{-1}$$
Les incertitudes-types sur les volumes prélevés sont estimées à 0,2 mL.
Par ailleurs, l’incertitude-type u(Cd) sur la concentration Cd se déduit des grandeurs mesurées par :
$\frac{u(C_d)}{C_d}= \sqrt{\left (\frac{u(V_E)}{V_E}\right)^2+\left (\frac{u(C_A)}{C_A}\right)^2+\left (\frac{u(V_D)}{V_D}\right)^2}$
Enfin, dans ces conditions expérimentales, le rapport entre la concentration 𝐶 de la solution S0 de la bouteille « d’ammoniaque » et son incertitude u(𝐶) est considéré comme étant le même qu’entre la concentration Cd de la solution diluée Sd et son incertitude u(Cd) :
$\frac{u(C)}{C}=\frac{u(C_d)}{C_d}$
10. Déterminer la valeur de l’incertitude-type u(𝐶) sur la concentration en ammoniac de la solution S0 commerciale. Écrire le résultat de la mesure de cette concentration 𝐶 avec son incertitude.
Le sujet nous donne deux formules :
Formule 1 : $$\frac{u\left(C_d\right)}{C_d}=\sqrt{\left(\frac{u(V_e)}{V_e}\right)^2+\left(\frac{u(C_a)}{C_a}\right)^2+\left(\frac{u(V_d)}{V_d}\right)^2}$$
Formule 2 : $$\frac{u\left(C\right)}{C}=\frac{u\left(C_d\right)}{C_d}$$
Déterminons $u\left(C\right)$ :
$$u\left(C\right)=C \times \frac{u\left(C_d\right)}{C_d}$$
Or la solution a été diluée 100 fois : $C=100 \times C_d$
D’où
$$u\left(C\right)=100 \times C_d \times \frac{u\left(C_d\right)}{C_d}$$
$$u\left(C\right)=100 \times u\left(C_d\right)$$
Or $$u\left(C_d\right)=C_d \times \sqrt{\left(\frac{u(V_e)}{V_e}\right)^2+\left(\frac{u(C_a)}{C_a}\right)^2+\left(\frac{u(V_d)}{V_d}\right)^2}$$
D’ou
$$u\left(C\right)=100 \times C_d \times \sqrt{\left(\frac{u(V_e)}{V_e}\right)^2+\left(\frac{u(C_a)}{C_a}\right)^2+\left(\frac{u(V_d)}{V_d}\right)^2}$$
$$u\left(C\right)=100 \times 7,40.{10}^{-2} \times \sqrt{\left(\frac{0,2}{14,8}\right)^2+\left(\frac{0,02}{5}\right)^2+\left(\frac{0,2}{10,0}\right)^2}$$
$$u\left(C\right)=0,2\ mol.L^{-1}$$
$$C=100 \times C_d=100 \times 7,40.{10}^{-2}=7,40\ mol.L^{-1}$$
$$C=7,40\pm0,2\ \ mol.L^{-1}$$
11. Confronter la valeur de la concentration déterminée expérimentalement avec l’indication de l’étiquette de la bouteille « d’ammoniaque » commerciale. Commenter.
D’après la question 10 la valeur de la concentration déterminée expérimentalement est comprise : $7,2\ mol.L^{-1}<C<7,6\ mol.L^{-1}$
L’indication de l’étiquette de la bouteille « d’ammoniaque » commerciale (question 6) $c_A=7,4\ mol.L^{-1}$ est bien comprise dans cet intervalle.
