Bac Amérique du Sud 2022 Sujet 2
Exercice A – (5 points) – Au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n°22-PYCJ2AS1
Sujet et corrigé
EXERCICE A. LE PLA OU ACIDE POLYLACTIQUE
Mots-clés : titrage avec suivi colorimétrique
Le PLA ou acide polylactique est un polymère dont la demande est croissante. Il est utilisé dans le secteur des emballages, des fibres, de la vaisselle jetable ou encore dans les matériaux d’impression pour les imprimantes 3D.
Il est souvent biosourcé car obtenu à partir de ressources renouvelables (amidon de maïs) et peut remplacer avantageusement de nombreux polymères pétrosourcés, car il possède des propriétés similaires à celles du PS (polystyrène) ou du PET (polyéthylène téréphtalate). De plus son recyclage chimique est possible. Il peut donc être une alternative à la pollution des milieux naturels par les plastiques.
1. La molécule d’acide lactique
On donne la formule topologique de la molécule d’acide lactique :
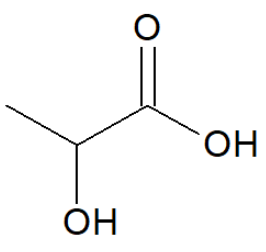
1.1. Dans la nomenclature officielle, l’acide lactique se nomme acide 2-hydroxypropanoïque. Justifier ce nom.
acide 2-hydroxy propanoïque.
2-hydroxy : car sur le 2ème atome de carbone de la chaine carbonée, il y a un groupe hydroxyle OH
propan : car la chaine carbonée comporte 3 atomes de carbone
acide oïque : car il y a un groupe carboxyle COOH
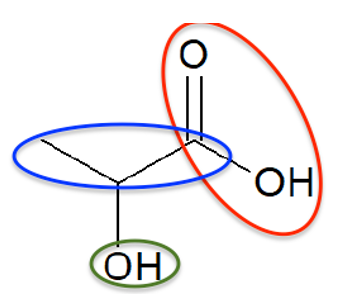
1.2. Écrire le couple acide base associé à l’acide lactique en utilisant les schémas de Lewis.
L’acide lactique est un acide. Il se transforme en base en perdant un proton H+ :
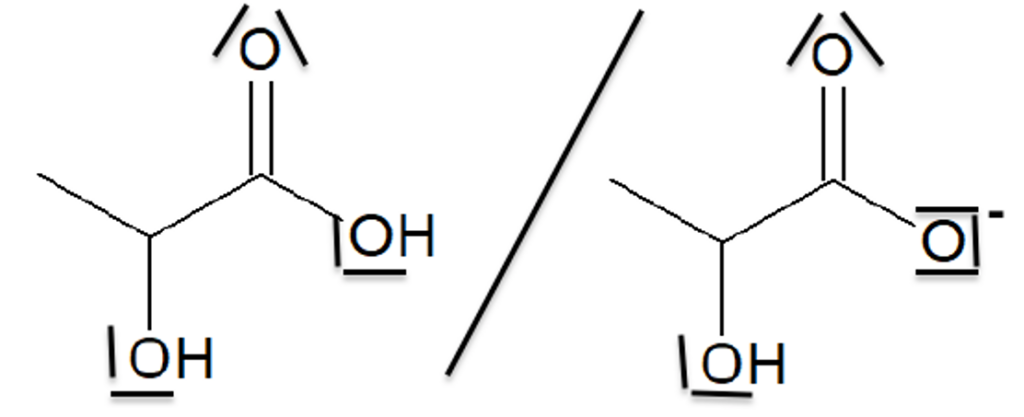
Une solution d’acide lactique de concentration en soluté apporté 𝐶 = 2,0 × 10–2 mol·L–1 a un pH égal à 2,8.
1.3. Indiquer si, dans ces conditions expérimentales, cet acide est fort ou faible. Justifier.
Pour un acide fort, l’acide réagit totalement avec l’eau : $\left[H_3O^+\right]=c$
$pH=-\log{\frac{\left[H_3O^+\right]}{c^0}}=-\log{c}$
Dans notre cas :
$-\log{c}=-\log{\left(2,0\times {10}^{-2}\right)}$
$-\log{c}=1,7$
$1,7\neq pH$
donc l’acide n’a pas réagit totalement avec l’eau, c’est un acide faible.
1.4. Écrire l’équation de la réaction qui modélise la transformation chimique entre l’acide lactique et l’eau, en notant AH l’acide lactique.
${\rm AH}{(aq)}+{H_2O}{(l)}\rightleftarrows A_{(aq)}^-+{H_3O}_{(aq)}^+$
2. Synthèse de l’acide polylactique (PLA)
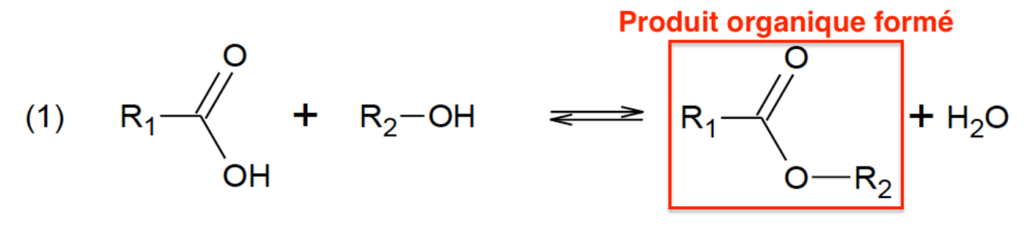
L’une des méthodes suivies pour la polymérisation industrielle de l’acide lactique utilise une réaction de type :

où R1 et R2 sont des groupes alkyles.
2.1. Citer la famille fonctionnelle à laquelle appartient le produit organique formé.
Le produit organique formé est un ester.
Les molécules d’acide lactique réagissent entre elles en chaîne selon l’équation de la réaction (1) et forment le PLA dont le début de la chaîne est représenté ci-après :

2.2. Parmi les groupements d’atomes encadrés, indiquer celui qui correspond au motif du polymère obtenu.
Le motif du polymère est le plus petit motif qui se répète dans la chaîne :

Le motif du polymère est le n°2.
3. Dégradation de l’acide polylactique (PLA)
Une dépolymérisation du PLA consiste à faire réagir le polymère avec du méthanol. Le PLA est ainsi transformé en lactate de méthyle. Celui-ci peut ensuite être transformé en lactide, pouvant reconduire ultérieurement au polymère, dans la perspective du recyclage du PLA.
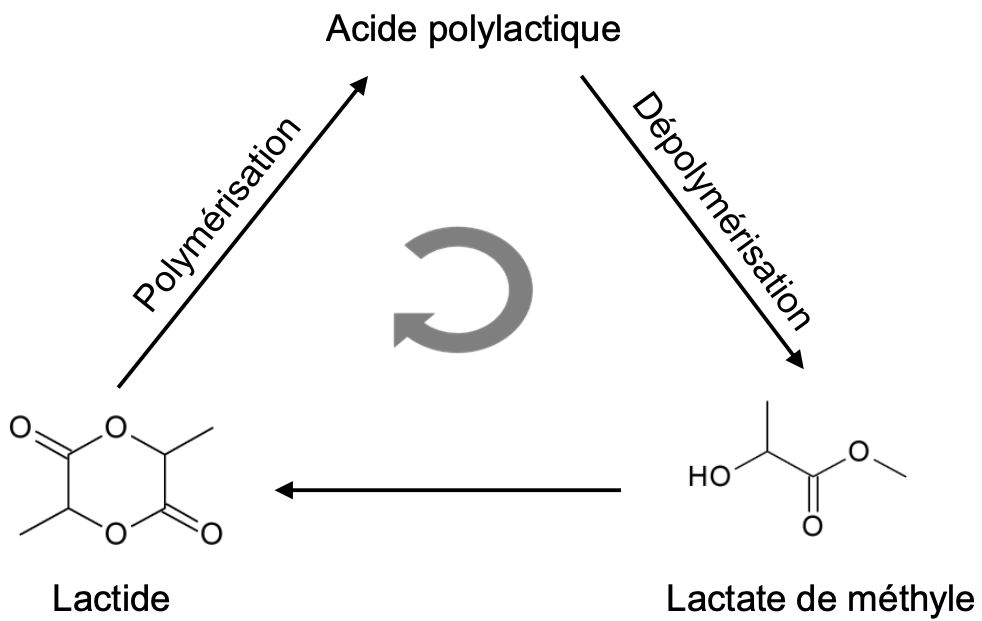
D’après Industrial & Engineering Chemistry Research https://pubs.acs.org/doi/10.1021/acs.iecr.0c01122#
La dépolymérisation du PLA est réalisée à différentes températures : 70 °C, 90 °C et 110 °C. On obtient les courbes suivantes :
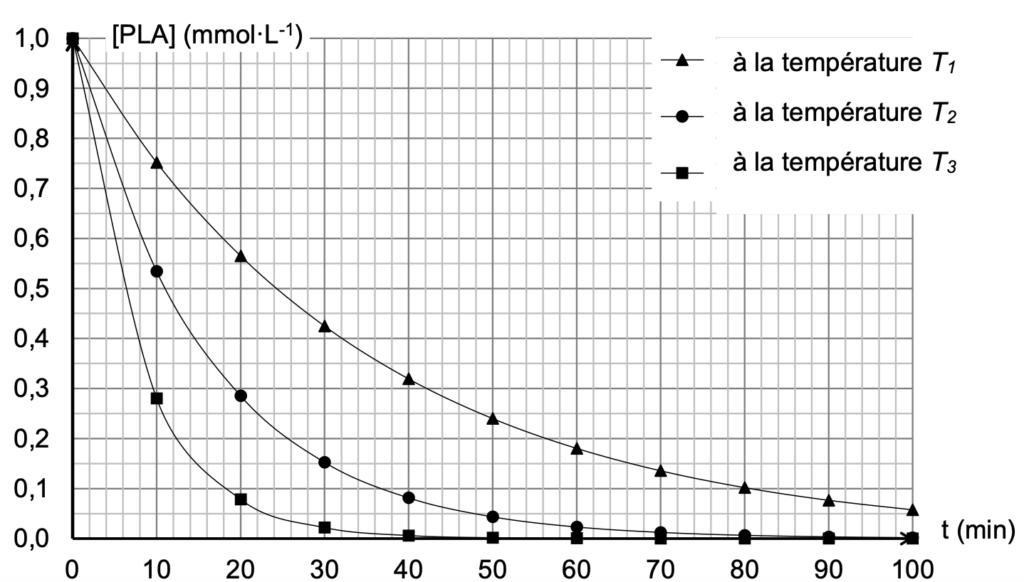
Figure 1. Étude de la dégradation chimique du PLA
3.1. Attribuer à 𝑇1, 𝑇2 et 𝑇3 la valeur de température correspondante. Justifier.
La température est un facteur cinétique. Plus la température est élevée, plus la réaction est rapide : plus la concentration de PLA atteint 0 mol.L-1 rapidement.
Donc
- T1=70°C
- T2=90°C
- T3=110°C
3.2. L’exploitation de la courbe obtenue à la température 𝑇1 permet d’obtenir les résultats suivants :
| Date 𝑡 (min) | 0 | 20 | 40 | 60 | 80 |
| [𝑃𝐿𝐴] (mol·L-1) | 1,0 × 10−3 | 5,6 × 10−4 | 3,2 × 10−4 | 1,8 × 10−4 | 1,0 × 10−4 |
| Vitesse volumique de disparition du PLA (mol·L-1 ·s-1) | ? | 2,7 × 10−7 | 1,5 × 10−7 | 8,5 × 10−8 | 4,8 × 10−8 |
3.2.1. Définir la vitesse volumique de disparition du PLA.
Vitesse volumique de disparition du PLA :
$v_d=-\frac{d\left[PLA\right]_{(t)}}{dt}$
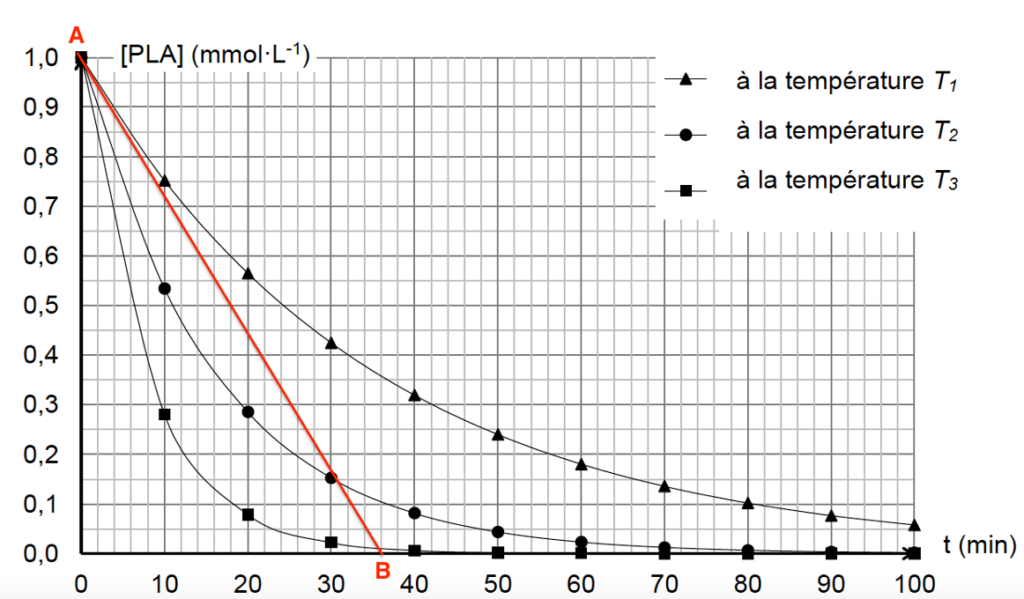
3.2.2. Déterminer graphiquement la valeur de la vitesse volumique de disparition du PLA à la date 𝑡 = 0 s pour la température 𝑇1 afin de compléter le tableau ci-dessus. Décrire la méthode utilisée.
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
Pour T1 à t=0 min :
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{0-1,0.{10}^{-3}}{\left(36-0\right)\times 60}=-4,6.{10}^{-7}mol.L^{-1}.s^{-1}$
$v_{t=0\ min}=-\frac{d\left[PLA\right]{(t)}}{dt}=-k$
$v{t=0\ min}=4,6.{10}^{-7}mol.L^{-1}.s^{-1}$
3.2.3. Montrer, en explicitant la démarche, que l’évolution de la concentration en PLA suit une loi de vitesse d’ordre 1.
Dans le cas d’une loi de vitesse d’ordre 1, la relation existante entre la vitesse volumique de disparition v du PLA , la concentration en PLA [PLA] et une constante de vitesse notée k est :
$v_d=k\times \left[PLA\ \right]_{(t)}$
Méthode 1 :
Faisons le rapport
| Date t (min) | 0 | 20 | 40 | 60 | 80 |
| [PLA] (mol·L-1) | 1,00E-03 | 5,60E-04 | 3,20E-04 | 1,80E-04 | 1,00E-04 |
| Vitesse volumique de disparition du PLA (mol·L-1 ·s-1) | 4,60E-07 | 2,70E-07 | 1,50E-07 | 8,50E-08 | 4,80E-08 |
| Rapport vd/[PLA] | 4,60E-04 | 4,82E-04 | 4,69E-04 | 4,72E-04 | 4,80E-04 |
Le rapport vd/[PLA] est quasiment constant : l’évolution de la concentration en PLA suit une loi de vitesse d’ordre 1.
Méthode 2 :
Traçons $v_d=f\left(\left[PLA\ \right]_{(t)}\right)$
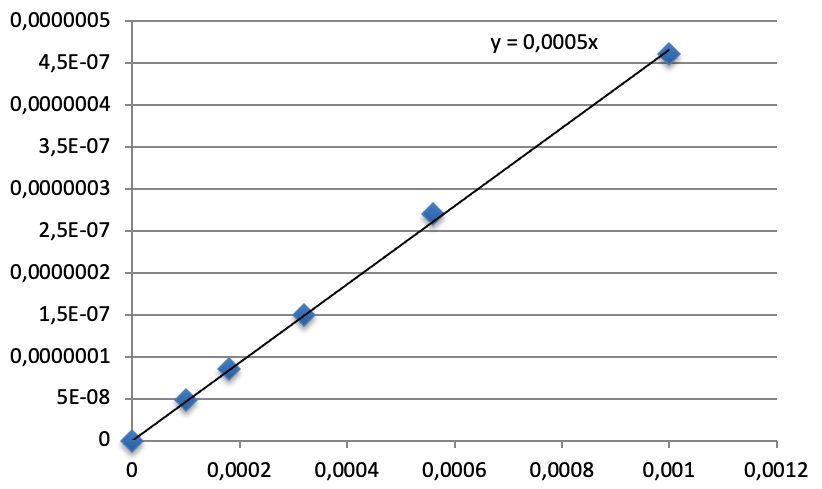
C’est une droite passant par l’origine :\ $v_d=k\times \left[PLA\ \right]_{(t)}$.
L’évolution de la concentration en PLA suit une loi de vitesse d’ordre 1.
