Polynésie 2022 Sujet 2
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n° 22-PYCJ2P01
Sujet et corrigé
Le sel d’oseille est une substance chimique présente sous forme d’un solide cristallin blanc, incolore et inodore. Il était historiquement extrait de certaines plantes telles que l’oseille ou la rhubarbe. On le nomme aussi, en nomenclature officielle, l’acide éthanedioïque ou plus communément acide oxalique. Cette substance est actuellement utilisée dans l’industrie pour la création de polymères mais peut être aussi employée dans de nombreux autres domaines : produit nettoyant, répulsif à frelon en apiculture, etc.
L’objectif de cet exercice est de valider deux hypothèses sur le type d’acidité de l’acide oxalique puis dans un second temps de retrouver la formulation de cet acide dans un produit ménager.
1. Première hypothèse : l’acide oxalique est un diacide fort.
Données :
- Tableau regroupant les électronégativités des atomes de carbone, d’oxygène et d’hydrogène :
| Carbone | Oxygène | Hydrogène | |
| Électronégativité | 2,55 | 3,44 | 2,20 |
- Formule semi-développée de l’acide oxalique :
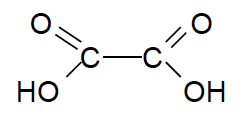
1.1. Donner la définition d’une espèce acide selon Brönsted puis, justifier le terme diacide pour l’acide oxalique.
Un acide est une espèce capable de céder un proton H+.
L’acide oxalique est un diacide car il est capable de céder deux protons H+.
1.2. Représenter sur votre copie la représentation de Lewis de l’acide oxalique ainsi que celle de l’une des deux autres formes acido-basiques. Justifier le caractère acide des atomes d’hydrogène dans la molécule.
Formule de Lewis de l’acide oxalique
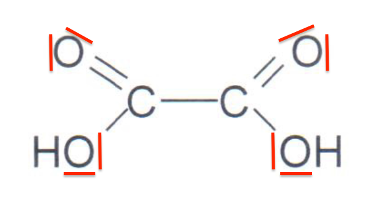
Formule de Lewis de l’une des formes acido-basiques de l’acide oxalique
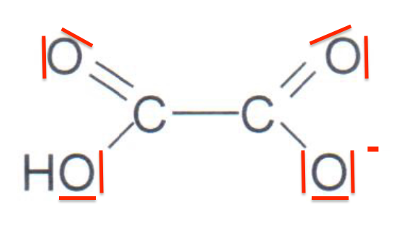
Chaque atome d’hydrogène de la molécule fait parti d’un groupe carboxyle. Ils ont tous un caractère acide.
1.3. Donner les deux couples acide/base associés à l’acide oxalique puis donner la particularité de l’espèce chimique présente dans les deux couples.
Acide oxalique $C_2H_2O_4$
Couples :
$C_2H_2O_4/C_2HO_4^-$
$C_2HO_4^-/C_2O_4^{2-}$
$C_2HO_4^-$ est la base du 1er couple et l’acide du 2nd : c’est une espèce amphotère.
Au laboratoire, on mesure la valeur du pH d’une solution d’acide oxalique de concentration en acide apporté C0 égale à 5,00×10 – 2 mol·L–1. La valeur du pH obtenu est de 1,47.
On souhaite modéliser la transformation chimique entre l’acide oxalique et l’eau en émettant l’hypothèse que l’acide oxalique se comporte comme un diacide fort. On notera AH2(aq) l’acide oxalique et A2–(aq) l’ion oxalate.
1.4. Écrire l’équation de la réaction modélisant cette transformation chimique.
$$AH_{2(aq)}+2H_2O_{(l)}\rightarrow A_{(aq)}^{2-}+2H_3O_{(aq)}^+$$
1.5. En déduire que, dans le cas de l’hypothèse précédente, la valeur de la concentration en quantité de matière en ions oxonium [H3O+] est égale à 1,00×10–1 mol·L–1. On pourra s’appuyer sur un tableau d’avancement.
L’acide oxalique est un diacide fort, la réaction avec l’eau est totale.
$$\frac{n_{H_3O^+}^f}{2}=\frac{n_{AH_2}^i}{1}$$
$$\frac{\left[H_3O^+\right]\times V}{2}=C_0\times V$$
$$\left[H_3O^+\right]=2C_0$$
$$\left[H_3O^+\right]=2\times 5,00.{10}^{-2}$$
$$\left[H_3O^+\right]=1,00.{10}^{-1}\ mol.L^{-1}$$
Donnée :
- La concentration standard c° est égale à 1,0 mol·L–1
1.6. À l’aide du résultat précédent, calculer la valeur du pH théorique de la solution puis, justifier l’hypothèse que l’acide oxalique est un diacide fort n’est pas valide.
$$pH=-\log\left(\frac{\left[H_3O^+\right]}{c^0}\right)$$
$$pH=-\log\left(\frac{1,00.{10}^{-1}}{1,0}\right)$$
$$pH=1,0$$
Cette valeur du pH a été trouvée en supposant que l’acide oxalique est un diacide fort.
Or ${\rm pH}_{exp}=1,47$.
La mesure du pH expérimentale est différente de celle calculée en supposant que l’acide oxalique est un diacide fort.
L’hypothèse que l’acide oxalique est un diacide fort n’est pas valide.
2. Deuxième hypothèse : l’acide oxalique se comporte comme un monoacide faible en solution.
Données :
- La concentration en acide apporté C0 de la solution d’acide oxalique est égale à 5,00×10–2 mol·L–1.
- Valeur du pKa de la première acidité : pKa1 = 1,2.
- Équation de la réaction associée à la première acidité :
AH2(aq) + H2O(l) ⇄ AH–(aq) + H3O+(aq)
- Rappel de la valeur expérimentale du pH de la solution d’acide oxalique : pHexp = 1,47.
2.1. Écrire l’équation de la réaction modélisant la transformation chimique de l’espèce AH– avec l’eau associée à la deuxième acidité.
$$AH_{(aq)}^-+H_2O_{(l)}\rightleftarrows A_{(aq)}^{2-}+H_3O_{(aq)}^+$$
2.2. À l’aide de la figure 1, déterminer la valeur du pKa de la deuxième acidité de l’acide oxalique.
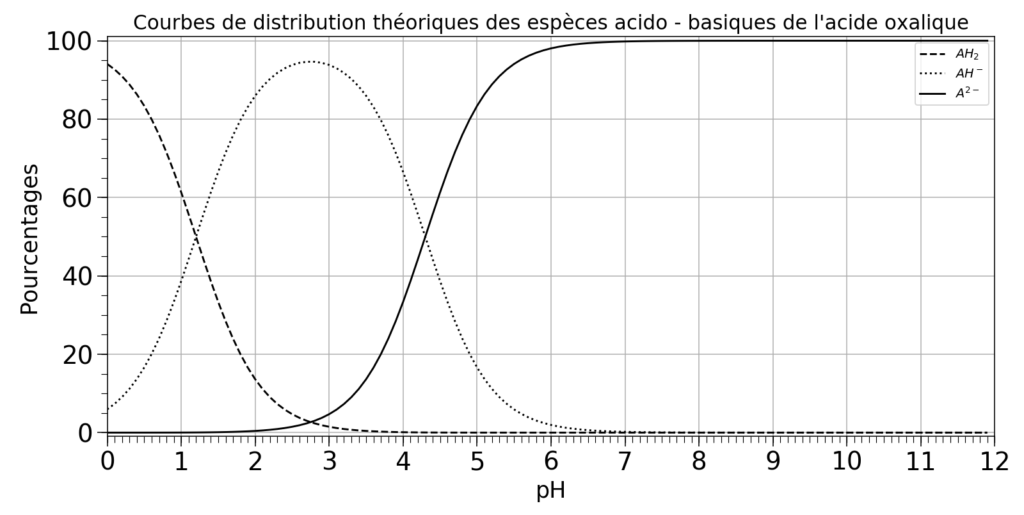
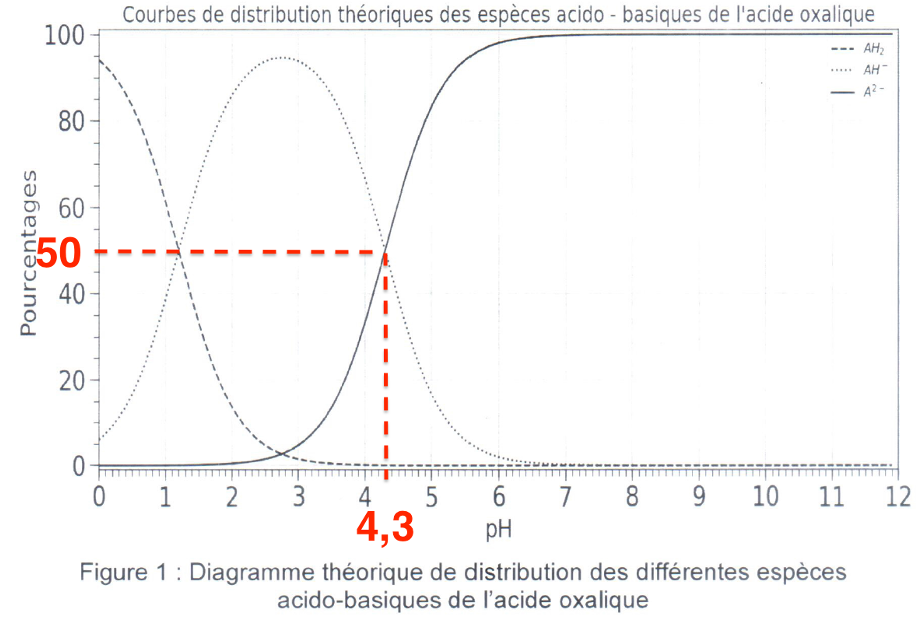
Figure 1 : Diagramme théorique de distribution des différentes espèces acido-basiques de l’acide oxalique
$$pH=pKa+\log\left(\frac{\left[Base\right]}{\left[Acide\right]}\right)$$
$$pH=pKa+\log\left(\frac{\left[A^{2-}\right]}{\left[{\rm HA}^-\right]}\right)$$
Lorsque
$$\left[A^{2-}\right]=\left[{\rm HA}^-\right]$$
$$\frac{\left[A^{2-}\right]}{\left[{\rm HA}^-\right]}=1$$
$$\log\left(\frac{\left[A^{2-}\right]}{\left[{\rm HA}^-\right]}\right)=0$$
$$pH=pKa$$
On lit donc $pKa=pH$ lorsque les courbes se croisent (autant d’acide que de base)
$pKa=4,3$
2.3. À l’aide de la figure 1 et de la valeur du pH réel de la solution, donner le pourcentage approximatif de chaque espèce présente dans la solution puis, justifier que l’on peut émettre l’hypothèse selon laquelle l’acide oxalique se comporte comme un monoacide.
Pour ${\rm pH}_{exp}=1,47$
Graphiquement :
$H_2A : 35%$
${\rm HA}^- : 65%$
$A^{2-} : 0%$
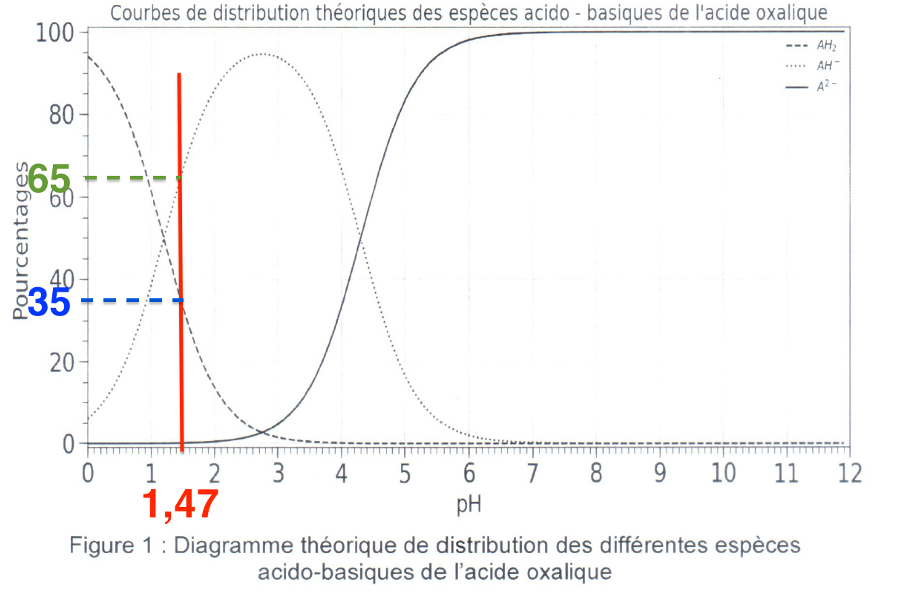
Il n’y a pas de $A^{2-}$, ainsi l’acide $H_2A$ ne donne qu’un seul proton pour se transformer en ${\rm HA}^-$, on peut donc émettre l’hypothèse que l’acide oxalique se comporte comme un monoacide.
Dans le cadre de cette deuxième hypothèse, nous allons essayer de retrouver la valeur du pH théorique de la solution.
2.4. À partir de l’équation de la réaction présentée en données, exprimer la constante d’acidité Ka1 en fonction de la concentration des différentes espèces chimiques à l’équilibre.
$$K_{a_1}=\frac{\left[{\rm HA}^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[H_2A\right]_{eq}\times c^0}$$
2.5. À l’aide la question précédente, justifier que la concentration en ion oxonium, notée h, vérifie l’équation du second degré suivante :
h² + Ka1·h – Ka1· C0 = 0 avec h = [H3O+]eq
$$K_{a_1}=\frac{\left[{\rm HA}^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[H_2A\right]{eq}\times c^0}$$
D’après le tableau d’avancement :
$$\left[{\rm HA}^-\right]{eq}=\left[H_3O^+\right]{eq}$$
$$\left[H_2A\right]{eq}=C_0-\left[H_3O^+\right]{eq}$$
$$K{a_1}=\frac{\left[H_3O^+\right]{eq}\times\left[H_3O^+\right]{eq}}{\left(C_0-\left[H_3O^+\right]{eq}\right)\times c^0}$$
$$K{a_1}=\frac{\left[H_3O^+\right]{eq}^2}{\left(C_0-\left[H_3O^+\right]{eq}\right)\times c^0}$$
$$\frac{\left[H_3O^+\right]{eq}^2}{\left(C_0-\left[H_3O^+\right]{eq}\right)\times c^0}=K_{a_1}$$
$$\left[H_3O^+\right]{eq}^2=K{a_1}\times\left(C_0-\left[H_3O^+\right]{eq}\right)\times c^0$$
$$\left[H_3O^+\right]{eq}^2=K_{a_1}\times C_0\times c^0-K_{a_1}\left[H_3O^+\right]{eq}\times c^0$$
$$\left[H_3O^+\right]{eq}^2-K_{a_1}\times C_0\times c^0+K_{a_1}\left[H_3O^+\right]_{eq}\times c^0=0$$
Or
$c^0=1,0$
Donc :
$$\left[H_3O^+\right]{eq}^2-K{a_1}\times C_0+K_{a_1}\left[H_3O^+\right]{eq}=0$$
Posons $h=\left[H_3O^+\right]{eq}$
$$h^2-K_{a_1}\times C_0+K_{a_1}h=0$$
On trouve :
$$h^2+K_{a_1}h-K_{a_1}\times C_0=0$$
Pour retrouver la concentration en ions oxonium, nous utilisons un code python incomplet donné en figure 2 permettant de calculer directement la concentration h en ions oxonium, ainsi que la valeur du pH théorique de la solution.
| code python | |
| 1 | import math |
| 2 | pKa1=float(input(« pKa1 du couple : « )) |
| 3 | concentration=float(input(« Concentration apportée en mol/L : « )) |
| 4 | Ka1= |
| 5 | ### Coefficients du polynome du deuxieme degre |
| 6 | a = 1 |
| 7 | b = Ka1 |
| 8 | c = -Ka1*concentration |
| 9 | ### Calcul du discriminant |
| 10 | Delta=b**2-4*a*c |
| 11 | ### Solution pour [H3O+] |
| 12 | h=(-b +sqrt(Delta))/(2*a) |
| 13 | ### pH final |
| 14 | pH = -math.log10(h) |
| 15 | ### Ecriture des resultats |
| 16 | print (‘h=’,format(h, »3.2E »), »mol/L », ‘ ‘, »pH final : »,round(pH,2)) |
| résultat du code |
h= 3.29E-02 mol/L pH final : 1.48 |
Figure 2. Code python permettant de calculer la concentration h en ions oxonium et la valeur du pH théorique de la solution.
2.6. Compléter la ligne 4 du code python par la formule permettant au programme de calculer la valeur de la constante d’acidité Ka1.
Ka1=10**(-pKa1)
2.7. À l’aide du résultat calculé par python et des données, justifier le fait que l’acide oxalique se comporte bien comme un monoacide faible.
Avec l’hypothèse que l’acide oxalique se comporte comme un monoacide, on obtient :
$$pH_{théorique}=1,48$$
Or
${\rm pH}{exp}=1,47$
Donc
$$pH{théorique}=pH_{exp}$$
L’acide oxalique se comporte bien comme un monoacide.
3. Formulation de l’acide oxalique.
Lors de l’achat de l’acide oxalique, on peut le trouver sous deux formes différentes. Dans un cas, il peut être pur et dans l’autre, il peut se trouver sous forme dihydratée. Un agent de laboratoire trouve un récipient contenant un solide blanc portant une étiquette avec la mention «acide oxalique» sans aucune autre précision.
Ne sachant pas si le produit est dihydraté ou non, il décide de faire un titrage par suivi pH-métrique d’une solution aqueuse de ce solide. Pour cela, il fabrique une solution connue par dissolution d’une masse d’acide oxalique m = 0,27 g avec une incertitude-type u(m) = 0,01 g dans une fiole jaugée de volume V = 100,0 mL avec une incertitude-type u(V) = 0,1 mL.
Données :
- L’incertitude u(X) sur une grandeur X lorsqu’elle est obtenue à partir d’autres grandeurs indépendantes s’écrit pour l’opération division :
si $X= \frac{Y}{Z}$ alors $u(X)= X \times \sqrt{\left (\frac{u(Y)}{Y}\right)^2+\left (\frac{u(Z)}{Z}\right)^2}$
u(X) est aussi appelée incertitude-type composée pour l’opération division. Les autres incertitudes-types sont souvent issues de l’évaluation de type B (une seule mesure).
- Tableau regroupant des informations sur les deux formulations de l’acide oxalique
| acide oxalique pur | acide oxalique dihydraté |
|
|---|---|---|
| formule brute | C2H2O4 | C2H2O4, 2H2O |
| masse molaire (g·mol– 1) | 90,0 | 126 |
| pictogramme de sécurité |  toxicité aigüe |  toxicité |
| utilisation | dans l’industrie | produit ménager |
3.1. Calculer la concentration en masse Cm de la solution fabriquée accompagnée de son incertitude-type u(Cm).
$$c_m=\frac{m}{V}$$
$$c_m=\frac{0,27}{100,0.{10}^{-3}}$$
$$c_m=2,7\ g.L^{-1}$$
$$u\left(c_m\right)=c_m.\sqrt{\left(\frac{u(m)}{m}\right)^2+\left(\frac{u(V)}{V}\right)^2}$$
$$u\left(c_m\right)=2,7\times\sqrt{\left(\frac{0,01}{0,27}\right)^2+\left(\frac{0,1}{100,0}\right)^2}$$
$$u\left(c_m\right)=0,1\ g.L^{-1}$$
$$c_m=2,7\pm0,1\ g.L^{-1}$$
L’équation support du titrage est : C2H2O4 + 2 HO– → C2O42– + 2 H2O
3.2. Justifier le coefficient 2 devant l’ion hydroxyde dans l’équation de réaction.
C’est un diacide, il libère 2 protons H+ , ainsi 2 HO– réagissent.
3.3. Donner une caractéristique indispensable de la transformation chimique afin que l’on puisse l’utiliser lors d’un dosage par titrage direct.
Pour qu’une réaction soit utilisée lors d’un titrage direct, il faut que la réaction soit totale.
3.4. Après avoir défini l’équivalence, donner la relation entre les quantités de matière des espèces titrée ntitrée et titrante ntitrante à l’équivalence.
L’équivalence est atteinte lorsque les réactifs sont introduits dans des proportions stœchiométriques.
$$\frac{n_{HO^-}^{eq}}{2}=\frac{n_{C_2H_2O_4}^i}{1}$$
$$\frac{n_{titrante}}{2}=n_{titrée}$$
L’agent de laboratoire prélève un volume V égal à 20,0 mL de la solution fabriquée précédemment. Il la titre à l’aide d’une solution d’hydroxyde de sodium de concentration en quantité de matière [ HO– ] = 0,10 mol·L–1.
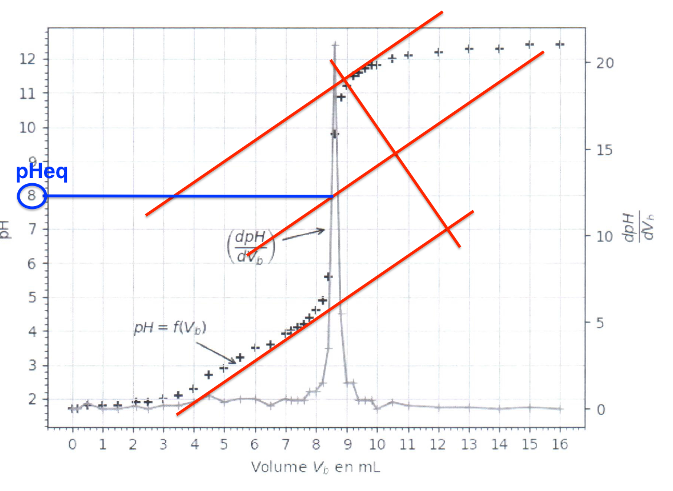
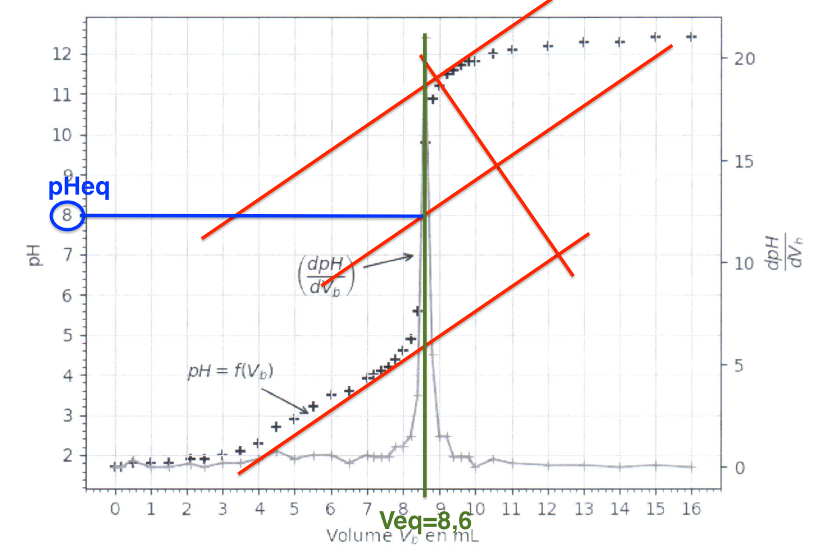
La courbe de dosage par titrage pH-métrique est présentée figure 3.

Figure 3 : Représentation graphique du pH et 𝑑𝑝𝐻/𝑑𝑉𝑏 en fonction du volume de solution d’hydroxyde de sodium lors du titrage de l’acide oxalique par les ions hydroxyde
Données :
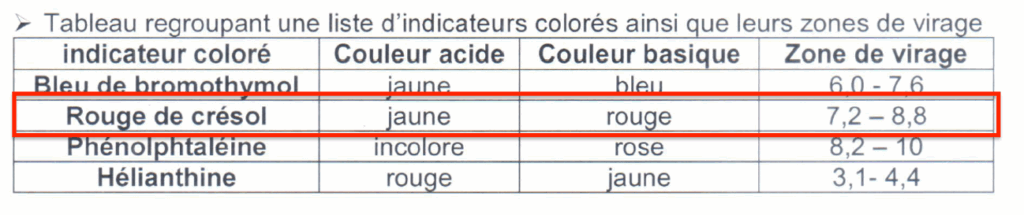
- Tableau regroupant une liste d’indicateurs colorés ainsi que leurs zones de virage
| indicateur coloré | Couleur acide | Couleur basique | Zone de virage |
| Bleu de bromothymol | jaune | bleu | 6,0 – 7,6 |
| Rouge de crésol | jaune | rouge | 7,2 – 8,8 |
| Phénolphtaléine | incolore | rose | 8,2 – 10 |
| Hélianthine | rouge | jaune | 3,1- 4,4 |
3.5. Proposer le nom d’un indicateur coloré convenable, ainsi que le changement de couleur obtenu lors de l’équivalence si l’agent de laboratoire avait choisi un titrage colorimétrique.
Trouvons ${\rm pH}{eq}$ à l’aide de la méthode des tangentes parallèles.
$${\rm pH}{eq}=8$$
Pour choisir un indicateur coloré, il faut que le ${\rm pH}_{eq}$ soit dans sa zone de virage.
Le rouge de crésol est un indicateur coloré convenable.
Changement de couleur : du jaune au rouge.
Pour la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche suivie est évaluée et nécessite d’être correctement présentée.
3.6. À l’aide de la figure 3, déterminer la concentration en quantité de matière en acide oxalique, puis justifier si le solide initial est dihydraté ou non.
$$\frac{n_{C_2H_2O_4}^i}{1}=\frac{n_{HO^-}^{eq}}{2}$$
$$C\times V=\frac{\left[HO^-\right]\times V_{eq}}{2}$$
$$C=\frac{\left[HO^-\right]\times V_{eq}}{2\times V}$$
Avec $V_{eq}=8,6\ mL$ (méthode des tangentes parallèles ou lecture graphique au pic de la dérivée)
$$C=\frac{0,10\times 8,6}{2\times 20,0}$$
$$C=2,2.{10}^{-2}\ mol.L^{-1}$$
Les masses molaires de l’acide oxalique pur et dihydraté sont différentes. Calculons la masse molaire :
$$c_m=C\times M$$
$$M=\frac{c_m}{C}$$
$$M=\frac{2,7}{2,2.{10}^{-2}}$$
$$M=123\ g.{\rm mol}^{-1}$$
Cette masse molaire correspond à celle de l’acide oxalique dihydraté.
