L’eau de boisson des poules

Bac La Réunion 2023 Sujet 1

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°23-PYCJ1LR1

Sujet et corrigé

EXERCICE I – L’EAU DE BOISSON DES POULES (9 points)

Dans un élevage, l’eau de boisson des poules doit être constamment traitée. Elle doit être désinfectée tout au long de la chaîne de distribution, par exemple avec du peroxyde d’hydrogène H₂O₂, aussi appelé eau oxygénée.

Afin d’éviter le développement d’une flore intestinale pathogène et de servir de vermifuge, le 𝑝𝐻 de l’eau doit être constamment maintenu entre 5,5 et 6,5.

Données :

• Masse molaire du peroxyde d’hydrogène : 𝑀(H₂O₂) = 34,0 g ⋅ mol⁻¹
• Couples d’oxydoréduction mis en jeu :
  • H₂O₂(aq) / H₂O(l)
  • O₂(g) / H₂O₂(aq)
  • MnO₄⁻(aq) / Mn²⁺(aq)
• Réaction de dismutation du peroxyde d’hydrogène :

2 H₂O₂(aq) ⇄ 2 H₂O(l) + O₂(g)

C’est une réaction spontanée mais lente à température ambiante, voire très lente à la température d’un réfrigérateur.

Le récipient contenant le peroxyde d’hydrogène doit être conservé à l’abri de la lumière afin de ne pas accélérer la réaction de dismutation.

• Valeurs de 𝑝𝐾_A à 25 °C du couple acide-base associé :
  • au peroxyde d’hydrogène :              H₂O₂(aq) / HO₂⁻(aq)              𝑝𝐾_A = 11,7 ;
  • à l’acide acétique :                            C₂H₄O₂(aq) / C₂H₃O₂⁻(aq)     𝑝𝐾_A = 4,8.
• Valeur de la concentration standard 𝐶^o = 1,0 mol ⋅ L⁻¹

PARTIE A : Le traitement de l’eau de boisson d’un élevage industriel de poules

L’oxydosane est un décontaminant et acidifiant des eaux de boisson pour animaux. Il est notamment utilisé dans les élevages de poules pondeuses.

C’est une solution composée notamment de peroxyde d’hydrogène. La concentration en masse en peroxyde d’hydrogène dans celle-ci est de 248 g⋅L⁻¹.

Mode d’emploi (d’après le fabricant GEOSANE) :

Norme 1 : Pour la désinfection et l’acidification (présence de poules dans l’élevage)

• Incorporer OXYDOSANE à raison de 100 mL à 200 mL pour un total de 1000 L d’eau.
• Dose à adapter en fonction du 𝑝𝐻 souhaité et de la désinfection nécessaire.

Norme 2 : Durant le vide sanitaire (absence de poules dans l’élevage)

• Incorporer OXYDOSANE à raison de 2,00 L pour un total de 100 L d’eau.
• Temps de contact : au minimum 1 h.
• Faire suivre d’un long rinçage.

A.  Décontamination de l’eau en fin de chaine des abreuvoirs

Afin de vérifier que l’eau de boisson de l’élevage est toujours désinfectée en fin de chaine, l’éleveur prélève 𝑉₁ = 20,00 ± 0,05 mL de cette eau et décide de déterminer sa concentration 𝑐₁ en quantité de matière de peroxyde d’oxygène H₂O₂ .

Pour cela, il procède au titrage du peroxyde d’oxygène présent dans le volume 𝑉₁ prélevé, par une solution de permanganate de potassium (K⁺(aq), MnO₄⁻ (aq)) acidifiée de concentration en quantité de matière d’ions permanganate égale à [MnO₄⁻]_𝑖 = 𝑐₀ = (1,00 ± 0,04) × 10⁻³ mol ⋅ L⁻¹.

L’équation de la réaction support du titrage est la suivante :

2 MnO₄⁻ (aq) + 6 H⁺(aq)  + 5 H₂O₂ (aq) →  2 Mn²⁺(aq)  + 8 H₂O (l) + 5 O₂ (g)

Lors de ce titrage colorimétrique, le volume obtenu à l’équivalence est de 𝑉_𝑒𝑞 = (6,60 ± 0,05) mL. L’incertitude type 𝑢(𝑐₁) sur la concentration 𝑐₁ se calcule à l’aide de la formule :

$$u(c_1)=c_1\sqrt{\left(\frac{u(V_{eq})}{V_{eq}}\right)^2+\left(\frac{u(V_1)}{V_1}\right)^2+\left(\frac{u(c_0)}{c_0}\right)^2}$$

Couleur des espèces chimiques en solution :

Ion permanganate MnO4−	Ion hydrogène H+	Peroxyde d’oxygène H2O2	Ion manganèse Mn2+
violette	incolore	incolore	incolore

A.1 Faire la liste du matériel nécessaire pour réaliser le titrage.

Liste du matériel nécessaire pour réaliser le titrage :

• Burette graduée
• Erlenmeyer.
• Agitateur magnétique + barreau aimanté
• Support pour la burette graduée.
• Pipette jaugée + pipeteur (pour le prélèvement de la solution titrée).

A.2 Écrire les demi-équations électroniques mises en jeu lors du titrage permettant de retrouver l’équation de la réaction d’oxydo-réduction support du titrage.

Couples :
$MnO_4^-\left(aq\right)/{\rm Mn}^{2+}\left(aq\right)$
$O_2\left(g\right)/H_2O_2\left(aq\right)$

Demi-équations électroniques :
$$2\times \ \ \ \ MnO_4^-\left(aq\right)+8H^+\left(aq\right)+5e^-={\rm Mn}^{2+}\left(aq\right)+4\ H_2O(l)$$
$$5\times \ \ \ \ O_2\left(g\right)+2H^+\left(aq\right)+2e^-=H_2O_2\left(aq\right)$$

$$2MnO_4^-\left(aq\right)+6H^+\left(aq\right)+5\ H_2O_2\left(aq\right)\rightarrow2{\rm Mn}^{2+}\left(aq\right)+5\ O_2\left(g\right)+8\ H_2O(l)$$

A.3 Définir l’équivalence du titrage et indiquer comment la repérer expérimentalement.

L’équivalence est atteinte lorsque les réactifs ont été introduits dans les proportions stœchiométriques.

Avant l’équivalence, les ions permanganate sont en défaut, la solution est incolore.
Après l’équivalence, les ions permanganate sont en excès, la solution est violette.
On repère l’équivalence lorsque la solution devient violette (changement de couleur).

A.4 Déterminer la valeur de la concentration 𝑐₁ et de son incertitude type associée 𝑢(𝑐₁).

A l’équivalence :
$$\frac{n_{H_2O_2}^i}{5}=\frac{n_{MnO_4^-}^{eq}}{2}$$
$$\frac{c_1\times V_1}{5}=\frac{c_0\times V_{eq}}{2}$$
$$c_1=\frac{5\times c_0\times V_{eq}}{2\times V_1}$$
$$c_1=\frac{5\times 1,00\times {10}^{-3}\times 6,60\times {10}^{-3}}{2\times 20,0\times {10}^{-3}}$$
$$c_1=8,25\times {10}^{-4}mol.L^{-1}$$

$$u(c_1)=c_1\times \sqrt{\left(\frac{u(V_{eq})}{V_{eq}}\right)^2+\left(\frac{u(V_1)}{V_1}\right)^2+\left(\frac{u(c_0)}{c_0}\right)^2}$$
$$u(c_1)=8,25\times {10}^{-4}\times \sqrt{\left(\frac{0,05}{6,60}\right)^2+\left(\frac{0,05}{20,0}\right)^2+\left(\frac{0,04}{1,00}\right)^2}$$
$$u(c_1)=4\times {10}^{-5}mol.L^{-1}$$

$$c_1=8,25\times {10}^{-4}\pm 4\times {10}^{-5}mol.L^{-1}$$
$$c_1=\left(8,25\pm 0,4\right)\times {10}^{-4}mol.L^{-1}$$

A.5 Indiquer quelle norme, 1 ou 2, l’éleveur a suivi.

L’oxydosane est une solution composée notamment de peroxyde d’hydrogène de concentration en masse
248 g ⋅ L⁻¹.
Calculons la concentration molaire :
$$c=\frac{c_m}{M}$$
$$c=\frac{248}{34,0}$$
$$c=7,29\ mol.L^{-1}$$

Norme 1 : Incorporer OXYDOSANE à raison de 100 mL à 200 mL pour un total de 1000 L d’eau.
Calculons la concentration obtenue par dilution pour la norme 1 :
$$n_f=n_m$$
$$c_f\times V_f=c_m\times V_m$$
$$c_f=\frac{c_m\times V_m}{V_f}$$
$$c_f=\frac{7,29\ \times 100\times {10}^{-3}}{1000}$$
$$c_f=7,29\times {10}^{-4}mol.L^{-1}\ $$

$$n_f=n_m$$
$${c\prime}_f\times V_f=c_m\times {V\prime}_m$$
$${c\prime}_f=\frac{c_m\times {V\prime}_m}{V_f}$$
$${c\prime}_f=\frac{7,29\ \times 200\times {10}^{-3}}{1000}$$
$${c\prime}_f=1,46\times {10}^{-4}mol.L^{-1}\ $$

Pour la norme 1 la $1,46\times {10}^{-4}mol.L^{-1}\ <c<7,29\times {10}^{-4}mol.L^{-1}\ $

Norme 2 : Incorporer OXYDOSANE à raison de 2,00 L pour un total de 100 L d’eau.
Calculons la concentration obtenue par dilution pour la norme 2 :

Lors d’une dilution la quantité de matière se conserve :
$$n_f=n_m$$
$$c_f\times V_f=c_m\times V_m$$
$$c_f=\frac{c_m\times V_m}{V_f}$$
$$c_f=\frac{7,29\ \times 2,00}{100}$$
$$c_f=1,46\times {10}^{-1}mol.L^{-1}\ $$

Lors du dosage nous avons trouvé $c_1=\left(8,25\pm 0,4\right)\times {10}^{-4}mol.L^{-1}$. L’éleveur a suivi la norme 1.

Le fabricant préconise de placer le bidon d’OXYDOSANE, une fois ouvert, dans un endroit sombre et frais. Il peut ainsi être conservé pendant un mois. Passé ce délai, la désinfection n’est plus garantie.

A.6 Justifier le mode de conservation.

Le peroxyde d’hydrogène subit une réaction de dismutation.
D’après l’énoncé : « C’est une réaction spontanée mais lente à température ambiante, voire très lente à la température d’un réfrigérateur. Le récipient contenant le peroxyde d’hydrogène doit être conservé à l’abri de la lumière afin de ne pas accélérer la réaction de dismutation. »
Pour que la concentration de peroxyde d’hydrogène ne diminue pas ou peu, il faut ralentir la réaction de dismutation.
La température est un facteur cinétique. C’est pourquoi le bidon d’OXYDOSANE, est conservé au frais.
De plus la lumière accélère la réaction. C’est pourquoi le bidon d’OXYDOSANE, est conservé dans un endroit sombre.

PARTIE B : Le traitement de l’eau de boisson des poules d’un particulier

Un particulier possédant des poules doit aussi acidifier l’eau de boisson pour le bien-être et la bonne santé de ses poules. Le 𝑝𝐻 de cette eau doit être de 6 environ. Pour cela, il dilue du vinaigre dans de l’eau et obtient ainsi une solution aqueuse d’acide acétique de concentration en quantité de matière 𝑐₃ = 1,60 × 10⁻³ mol⋅L⁻¹.

B.1.  Étude de la formule de la molécule d’acide acétique

B.1.1 Écrire la formule topologique de l’acide acétique.

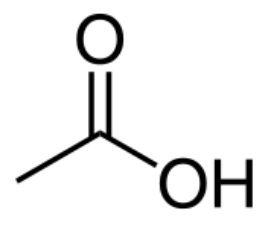
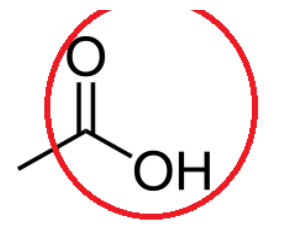
B.1.2 Entourer le groupe fonctionnel et nommer la famille à laquelle il appartient.

B.1.3 Donner le nom de l’acide acétique dans la nomenclature internationale.

Nom de l’acide acétique dans la nomenclature internationale : Acide éthanoïque

B.2.  L’acide acétique en solution

L’équation de la réaction modélisant la transformation chimique entre l’acide acétique et l’eau s’écrit :

C₂H₄O₂(aq)  +  H₂O (l)    ⇄     C₂H₃O₂⁻ (aq) +  H₃O⁺(aq)

B.2.1 Représenter le diagramme de prédominance associé au couple C₂H₄O₂(aq) / C₂H₃O₂⁻ (aq).

Diagramme de prédominance :

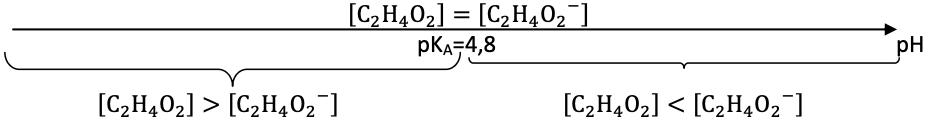
B.2.2 Exprimer la constante d’acidité 𝐾_A du couple C₂H₄O₂(aq) / C₂H₃O₂⁻ (aq).

$$K_A=\frac{\left[{C_2H_4O_2}^-\right]{eq}\times \left[H_3O^+\right]{eq}}{\left[C_2H_4O_2\right]_{eq}\times c^0}$$

B.2.3 À partir de l’expression de la constante d’acidité 𝐾_A, retrouver la relation :

$$pH=pK_A+\log\left(\frac{[C_2H_3O_2^-(aq)]}{[C_2H_4O_2(aq)]}\right)$$

$$K_A=\frac{\left[{C_2H_4O_2}^-\right]{eq}\times \left[H_3O^+\right]{eq}}{\left[C_2H_4O_2\right]{eq}\times c^0}$$
$${\rm pK}A=-log\left(K_A\right)$$
$${\rm pK}A=-log\left(\frac{\left[{C_2H_4O_2}^-\right]{eq}\times \left[H_3O^+\right]{eq}}{\left[C_2H_4O_2\right]{eq}\times c^0}\right)$$
$${\rm pK}A=-log\left(\frac{\left[H_3O^+\right]{eq}}{c^0}\right)-log\left(\frac{\left[{C_2H_4O_2}^-\right]{eq}}{\left[C_2H_4O_2\right]{eq}}\right)$$
$${\rm pK}A=pH-log\left(\frac{\left[{C_2H_4O_2}^-\right]{eq}}{\left[C_2H_4O_2\right]{eq}}\right)$$
$$pH-log\left(\frac{\left[{C_2H_4O_2}^-\right]{eq}}{\left[C_2H_4O_2\right]_{eq}}\right)={\rm pK}A$$
$$pH={\rm pK}A+log\left(\frac{\left[{C_2H_4O_2}^-\right]{eq}}{\left[C_2H_4O_2\right]{eq}}\right)$$

B.2.4 Calculer le 𝑝𝐻 réel de cette solution et vérifier si le particulier respecte la norme d’acidification pour l’eau de boisson de ses poules.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’est pas aboutie. La démarche est évaluée et nécessite d’être correctement présentée.

	$${C_2H_4O_2}{(aq)}$$	$$H_2O{(l)}\rightleftarrows$$	$${{C_2H_4O_2}^-}{(aq)}$$	$$+{H_3O}{(aq)}^+$$
État initial	$c_3$	Solvant	0	0
État intermédiaire	$c_3V-x$	Solvant	$x$	$x$
État final	$c_3V-x_f$	Solvant	$x_f$	$x_f$

$$K_A=\frac{\left[{C_2H_4O_2}^-\right]{eq}\times \left[H_3O^+\right]{eq}}{\left[C_2H_4O_2\right]_{eq}\times c^0}$$

$$\left[{C_2H_4O_2}^-\right]{eq}=\frac{n{{C_2H_4O_2}^-}}{V}=\frac{\mathbf{x}\mathbf{f}}{V}$$
$$\left[C_2H_4O_2\right]{eq}=\frac{n_{C_2H_4O_2}}{V}=\frac{\mathbf{c}\mathbf{3}\mathbf{V}-\mathbf{x}\mathbf{f}}{V}$$

$$K_A=\frac{\frac{x_f}{V}\times \left[H_3O^+\right]{eq}}{\frac{c_3V-x_f}{V}\times c^0}$$
$$K_A=\frac{\frac{x_f}{V}\times \left[H_3O^+\right]{eq}}{\left(\frac{c_3V}{V}-\frac{x_f}{V}\right)\times c^0}$$
$$K_A=\frac{\frac{x_f}{V}\times \left[H_3O^+\right]_{eq}}{\left(c_3-\frac{x_f}{V}\right)\times c^0}$$

Or
$$\left[H_3O^+\right]{eq}=\frac{n{H_3O^+}}{V}=\frac{x_f}{V}$$

D’où
$$K_A=\frac{\frac{x_f}{V}\times \left[H_3O^+\right]{eq}}{C-\frac{x_f}{V}\times c^0}$$
$$K_A=\frac{\left[H_3O^+\right]{eq}\times \left[H_3O^+\right]{eq}}{\left(c_3-\left[H_3O^+\right]{eq}\right)\times c^0}$$
$$K_A\times \left(c_3-\left[H_3O^+\right]{eq}\right)\times c^0={\left[H_3O^+\right]{eq}}^2$$
$$-{\left[H_3O^+\right]{eq}}^2+K_A\times \left(c_3-\left[H_3O^+\right]{eq}\right)\times c^0=0$$
$$-{\left[H_3O^+\right]{eq}}^2+K_A\times c_3 \times c^0-K_A\times \left[H_3O^+\right]{eq}\times c^0=0$$
$$-{\left[H_3O^+\right]{eq}}^2-K_A\times \left[H_3O^+\right]{eq}\times c^0+K_A\times c_3\times c^0=0$$

On remplace par les valeurs numériques :
$K_A={10}^{-pKa}={10}^{-4,8}=1,6\times {10}^{-5}$
$c^0=1$
$c_3=1,6\times {10}^{-3}$

$$-{\left[H_3O^+\right]{eq}}^2-1,6\times {10}^{-5}\times \left[H_3O^+\right]{eq}\times 1+1,6\times {10}^{-5}\times 1,6\times {10}^{-3}\times 1=0$$
$$-{\left[H_3O^+\right]{eq}}^2-1,6\times {10}^{-5}\times \left[H_3O^+\right]{eq}+2,6\times {10}^{-8}=0$$

C’est une équation du second degré :
$$\Delta=b^2-4ac$$
$$\Delta=\left(-1,6\times {10}^{-5}\right)^2-4\times -1\times 2,6\times {10}^{-8}$$
$$\Delta=1,0\times {10}^{-7}$$
$$\left[H_3O^+\right]_1=\frac{-b+\sqrt{\Delta}}{2a}$$
$$\left[H_3O^+\right]_1=\frac{-\left(-\ 1,6\times {10}^{-5}\right)+\sqrt{1,0\times {10}^{-7}}}{2\times -1}$$
$$\left[H_3O^+\right]_1=-1,7\times {10}^{-4}\ mol.L^{-1}$$

$$\left[H_3O^+\right]_2=\frac{-b-\sqrt{\Delta}}{2a}$$
$$\left[H_3O^+\right]_2=\frac{-\left(-\ 1,6\times {10}^{-5}\right)-\sqrt{1,0\times {10}^{-7}}}{2\times -1}$$
$$\left[H_3O^+\right]_2=1,5\times {10}^{-4}\ \ mol.L^{-1}$$

On ne garde pas la valeur négative.
$$\left[H_3O^+\right]=1,5\times {10}^{-4}\ \ mol.L^{-1}$$

$$pH=-log\left(\frac{\left[H_3O^+\right]_{eq}}{c^0}\right)$$
$$pH=-log\left(\frac{1,5\times {10}^{-4}\ \ }{1}\right)$$
$$pH=3,8$$

D’après l’énoncé : « Un particulier possédant des poules doit aussi acidifier l’eau de boisson pour le bien-être et la bonne santé de ses poules. Le pH de cette eau doit être de 6 environ. »
Le particulier ne respecte pas la norme d’acidification pour l’eau de boisson de ses poules.