Bac Amérique du nord 2022 Sujet 1
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1AN1
Sujet et corrigé
EXERCICES AU CHOIX DU CANDIDAT
Vous indiquerez sur votre copie les 2 exercices choisis : exercice A ou exercice B ou exercice C.
EXERCICE A : L’EPAISSEUR DU MATELAS DU SAUT A LA PERCHE (5 POINTS)
Mots-clés : mouvement dans un champ de pesanteur uniforme, aspects énergétiques, langage de programmation Python
Armand Duplantis est un athlète américano-suédois. Depuis février 2020, il détient le record du monde de saut à la perche en ayant franchi une barre à 6,18 m.
Le principe du saut à la perche repose sur la conversion de l’énergie cinétique, issue de la course d’élan du perchiste, en énergie potentielle de pesanteur.
L’athlète plante la perche en bas du sautoir et la plie. L’énergie cinétique issue de la course est alors transformée en énergie élastique et emmagasinée par la perche. Lorsque celle-ci se détend, elle restitue cette énergie élastique à l’athlète. On passe ainsi d’un mouvement horizontal, la course, à un mouvement vertical, le saut. Aujourd’hui, les perches en fibre de carbone restituent de manière quasiment intégrale l’énergie emmagasinée.
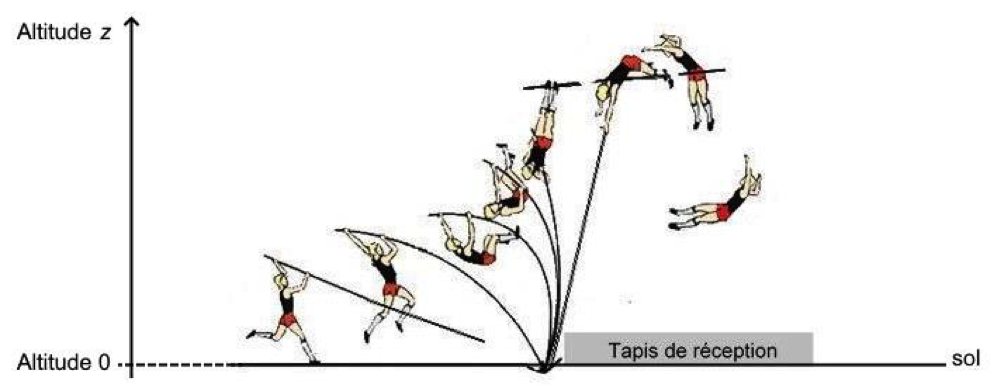
Différentes phases lors du saut à la perche
Dans cet exercice, il s’agit d’étudier les transferts d’énergie lors de la phase d’ascension, de déterminer la vitesse d’impact de l’athlète sur le tapis et de vérifier que l’épaisseur du matelas de réception évite que l’athlète ne se blesse.
Dans tout l’exercice, on assimile l’athlète à son centre de masse et on note z l’altitude par rapport au sol.
Données :
- masse de l’athlète : m = 79,0 kg ;
- intensité de la pesanteur terrestre : g = 9,81 N·kg-1.
A. Étude de la phase ascendante
Le mouvement complet d’Armand Duplantis, lors de son record du monde, est filmé puis étudié à l’aide d’un logiciel de pointage. Les données de la partie ascendante du mouvement sont traitées à l’aide d’un programme écrit en langage python qui permet de représenter l’évolution au cours du temps des énergies cinétique Ec, potentielle de pesanteur Epp, potentielle élastique Epe et mécanique Em du système défini par l’ensemble {sportif + perche}. Un extrait de ce programme est donné ci-dessous :
1 from math import *
2 import numpy as np
3 import matplotlib.pylab as plt
4
5 # Nombre de points de mesure
6 Np=21
7
8 #Valeurs des constantes
9 m=79.0 # en kilogramme
10 g=9.81 # en newton par kilogramme
11
12 # tableaux de valeurs contenant les valeurs de temps t en seconde,
13 # de hauteur z en mètre et de vitesse v du centre de gravité en mètre par seconde
14 t =np.array( [0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2])
15 z =np.array([1,1.032,1.058,1.118, liste incomplète])
16 v =np.array([10.063,9.522,8.512,7.365,6.463,5.695,5.032,4.5,3.897,3.464,3.212, liste incomplète])
17
18 # initialisation des énergies
19 Em =np.zeros(21)
20 Ec =np.zeros(21)
21 Epp =np.zeros(21)
22 Epe =np.zeros(21)
23
24 # calculs des valeurs des différentes énergies en fonction du temps
25 for i in range(0,Np) :
26 Em[i]=4775.0
27 Ec[i]= ………. # A compléter
28 Epp[i]=……… # A compléter
Extrait du programme écrit en langage python
Pour la partie ascendante du mouvement de l’athlète, on obtient les courbes suivantes :
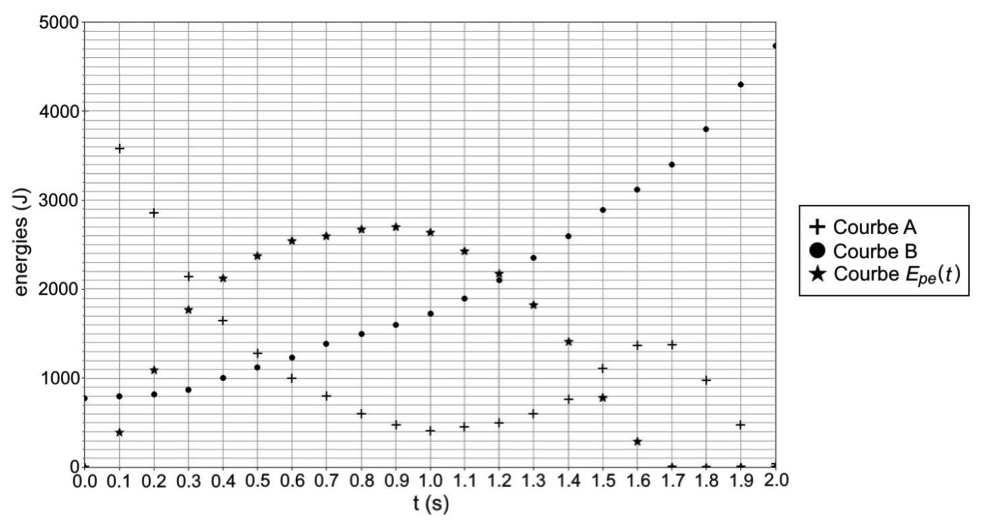
Courbes obtenues à l’aide du programme écrit en langage python
A.1. Identifier parmi les courbes A et B, celle représentant l’énergie cinétique et celle représentant l’énergie potentielle de pesanteur. Justifier les choix
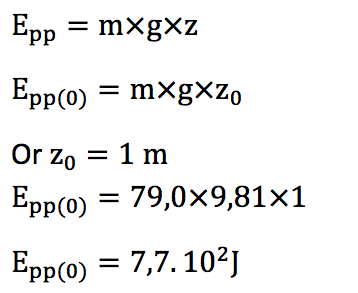
Initialement l’énergie de la courbe B est 7,7.102J. La courbe B représente l’énergie potentielle de pesanteur.
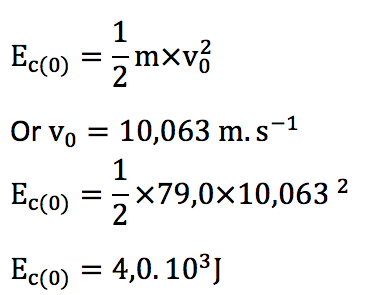
Initialement l’énergie de la courbe A est 4,0.103J. La courbe A représente l’énergie cinétique.
A.2. Recopier et compléter le code des lignes 27 et 28 du programme
Ligne 27 Ec[i]= 0,5*m*v[i]**2 # A compléter
Ligne 28 Epp[i]= m *g*z[i] # A compléter
A.3. Extraire du programme la valeur de la vitesse initiale d’Armand Duplantis.
Vitesse initiale d’Armand Duplantis : v0 = 10,063 m∙s-1.
L’énergie potentielle élastique augmente avec la déformation de la perche.
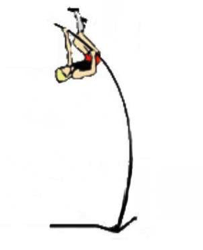
A.4. Identifier, parmi les trois situations ci-dessous, celle qui correspond à t = 0,9 s. Justifier.
| Situation 1 | Situation 2 | Situation 3 |
 |  |  |
Le sauteur à la perche dans différentes situations
à t = 0,9 s , l’énergie potentielle élastique est maximale.
Or l’énergie potentielle élastique augmente avec la déformation de la perche.
Ainsi la déformation de la perche est maximale à t = 0,9 s : Situation 2.
Armand Duplantis franchit la barre grâce à une technique d’enroulement. Ainsi, son centre de masse se situe en un point A légèrement au-dessous de la barre au moment du franchissement.
A.5. En exploitant le graphique précédent, déterminer la valeur de l’altitude maximale zA, par rapport au sol, atteinte par le centre de masse de l’athlète.
La valeur de l’altitude maximale zA, est atteinte pour Epp(A) max. Graphiquement : Epp(A)= 4750 J
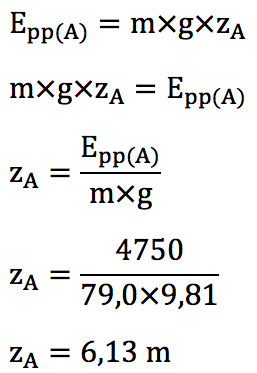
B. La vitesse d’impact sur le tapis de réception
Au moment du franchissement de la barre, le centre de masse de l’athlète se situe à l’altitude zA et sa vitesse est considérée comme nulle.
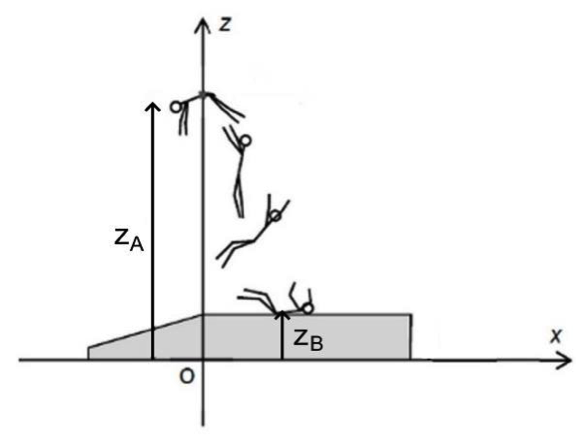
On note zB l’altitude du centre de masse de l’athlète au moment de son impact avec le tapis. On négligera l’action de l’air.
B.1. Justifier qu’après le franchissement de la barre, l’athlète est en chute libre.
D’après le texte : « On négligera l’action de l’air. »
L’athlète ne tient plus la perche, il n’est soumis qu’a son poids : il est en chute libre.
B.2. En utilisant le théorème de l’énergie cinétique ou la loi de conservation de l’énergie mécanique, déterminer l’expression de la vitesse d’impact de l’athlète sur le tapis en fonction de g, zA et zB.
Méthode 1 : Théorème de l’énergie cinétique
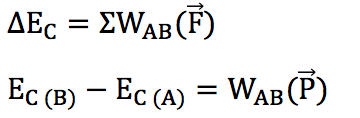
Or “Au moment du franchissement de la barre, le centre de masse de l’athlète se situe à l’altitude ZA et sa vitesse est considérée comme nulle.”
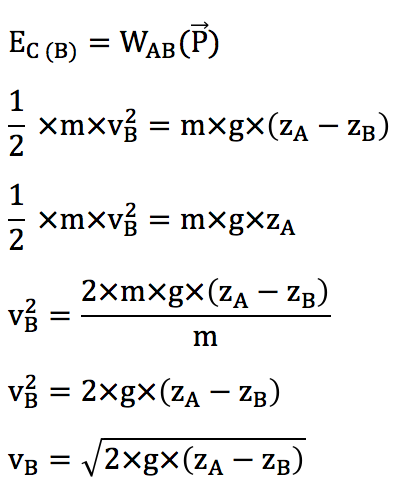
Méthode 2 : Loi de conservation de l’énergie mécanique : nous sommes en chute libre, il n’y a pas de frottements , l’énergie mécanique se conserve.
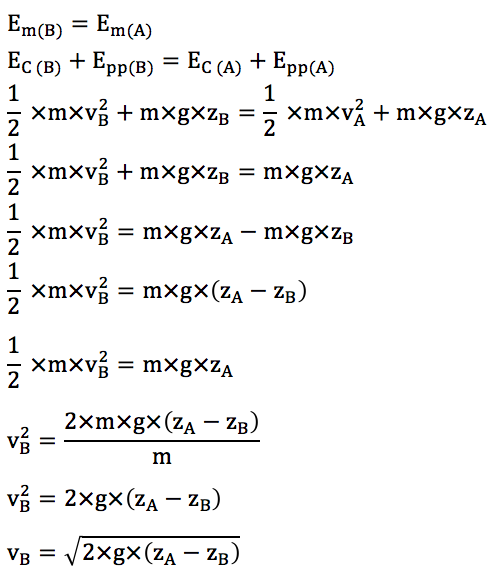
On donne zB – zA = 5,31 m.
B.3. Calculer la valeur de la vitesse d’impact de l’athlète.
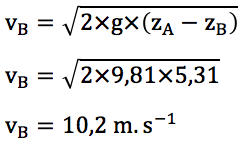
C. Épaisseur du matelas
On considère le repère (Oxz) représenté sur le schéma précédent.
Au moment où l’athlète arrive sur le matelas, son centre de masse est animé d’une vitesse v⃗0 dont la composante verticale est v0z = -10,2 m∙s-1.
On considère que la composante horizontale de la vitesse est nulle : v0x = 0.
On modélise l’action du matelas sur l’athlète par une force constante F⃗ T verticale vers le haut. Pour ne pas provoquer de blessures lors de la phase de réception, le matelas se déforme pour que
la valeur de l’accélération subie par le corps de l’athlète ne dépasse pas 10 fois l’accélération de la pesanteur, soit 10 × g.
On se place dans le cas où l’accélération est maximale : az = 10 × g.
C.1. Après avoir fait un bilan des forces s’exerçant sur Armand Duplantis lors de la réception et en utilisant la seconde loi de Newton, démontrer que la valeur FT de la force exercée par le tapis est égale à 8,52 kN.
Bilan des forces s’exerçant sur Armand Duplantis :
- Le poids
- l’action du matelas sur l’athlète
D’après la 2nd Loi de Newton :

C.2. En prenant l’instant du contact entre l’athlète et le tapis comme origine des temps et en se plaçant dans le repère (Oxz), montrer que les équations horaires du mouvement de l’athlète s’écrivent :
vz(t) = 10 × g × t + v0z
z(t) = 5 × g × t 2 + v0z × t + zB


C.3. Déterminer la durée de la phase de réception.
La durée de la phase de réception : temps pour lequel vz(tréception)=0 , il faut que l’athlète s’arrête.
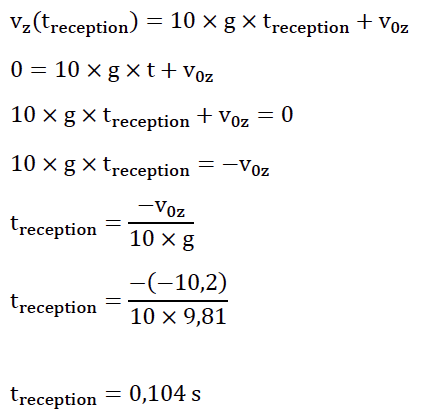
Le tapis de réception a une épaisseur de 82 cm.
C.4. Montrer que cette épaisseur est suffisante pour que l’athlète ne soit pas blessé par le sol.
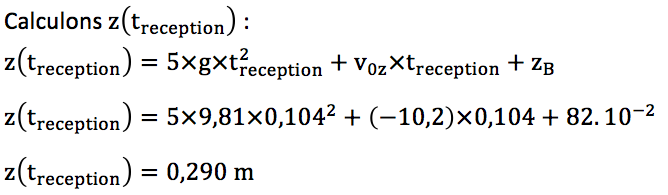
z(tréception)>0, cette épaisseur est donc suffisante pour que l’athlète ne soit pas blessé par le sol.
