Performances des bolomètres de Planck

Polynésie 2025 Sujet 1

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ1PO1

« Le satellite Planck est un satellite de l’Agence Spatiale Européenne (ESA) qui a fourni des cartes de tout le ciel dans le domaine sub-millimétrique et radio (30 à 850 GHz). L’objectif du satellite Planck a été d’analyser, avec la plus haute précision jamais atteinte, les restes du rayonnement qui remplissait l’Univers juste après le Big Bang, ce que nous observons aujourd’hui comme le Fond Diffus Cosmologique. » 
D’après https://www.ias.u-psud.fr/fr/content/planck-hfi

Dans la suite du sujet, le Fond Diffus Cosmologique sera noté CMB (de l’anglais, Cosmic Microwave Background). Les mesures du CMB sont réalisées par des bolomètres qui permettent de mesurer la puissance transportée par un rayonnement électromagnétique.

L’objectif de cet exercice est d’étudier les performances d’un des bolomètres du satellite Planck.

Données :

• célérité de la lumière : c = 3,00×10⁸ m·s^–1 ;
• différents domaines du spectre électromagnétique :

Nom du domaine	Rayon X	Ultraviolet	Visible	Infrarouge	Micro- onde	Radio
Domaine de longueur d’onde λ	de 0,01 à 100 nm	de 10 à 400 nm	de 400 à 800 nm	de 0,8 à 1 mm	de 1 à 300 mm	de 0,1 à 1 km

Le CMB se caractérise par un rayonnement thermique de température caractéristique T_CMB = 2,725 K. Afin d’étudier les variations de température autour de cette valeur, le satellite Planck est équipé d’un bolomètre sensible au rayonnement de fréquence f₀ = 217 GHz.

Q1. Calculer la longueur d’onde λ₀ correspondant à la fréquence f₀ et nommer le domaine du spectre auquel appartient l’onde électromagnétique associée au CMB.

Données :

• la puissance P_CN reçue par une surface S soumise au rayonnement d’un corps à la température T_CN est donnée par : P_CN = σ⋅T ⁴ ⋅S où σ est la constante de Stefan-Boltzmann, σ = 5,67×10–8 W·m–2·K–4 ;
• la surface de la partie sensible au CMB vaut S_CMB = 9,93×10^–8 m². Pour étudier le CMB autour de la fréquence f₀, un filtre est placé devant cette surface, il sélectionne 25,2 % de la puissance reçue.

Q2. Montrer que la puissance P_CMB reçue par le bolomètre de la part du CMB au travers du filtre vaut P_CMB = 7,82×10^–14 W.

Les bolomètres, comme indiqué sur le schéma simplifié ci-après, sont composés d’une partie sensible au rayonnement et d’un thermostat. L’énergie cédée par le rayonnement à la partie sensible provoque une élévation de sa température. Cette

partie sensible est en contact avec un thermostat plus froid qui permet d’évacuer l’énergie reçue, le matériau permettant le contact possède une résistance thermique R_contact.

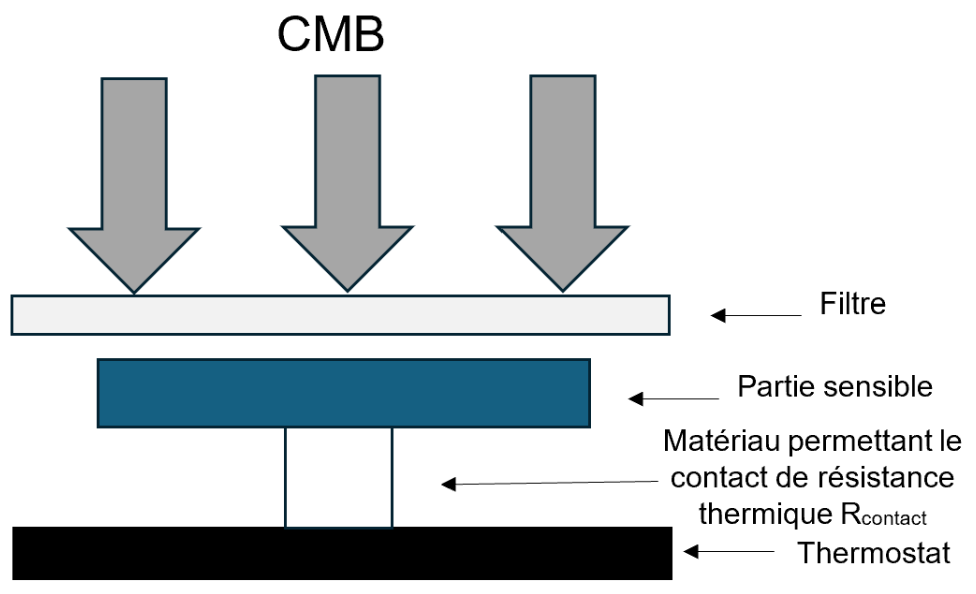
Schéma simplifié d’un bolomètre.

On cherche à modéliser l’évolution de la température de la partie sensible en fonction du temps par un bilan d’énergie. On note T_T la température du thermostat et T la température de la partie sensible du bolomètre.

Donnée :

• la puissance Psyst reçue par un système à la température Tsyst en contact avec un thermostat à la température T0 par l’intermédiaire d’une résistance thermique Rth s’exprime :

$$P_{\mathrm{syst}} = -\frac{(T_{\mathrm{syst}}-T_0)}{R_{\mathrm{th}}}$$

Q3. Exprimer la puissance P_T reçue par la partie sensible du bolomètre de la part du thermostat en fonction des grandeurs associées au bolomètre qui sont T, T_T et R_contact. Justifier le signe de la valeur de cette grandeur.

Q4. Exprimer le transfert thermique Q_tot échangé par la partie sensible du bolomètre avec l’ensemble des sources extérieures pendant une durée Δt en fonction de P_CMB, T, T_T, Δt et R_contact. On admettra que, pendant la durée Δt, la puissance reçue de la part du thermostat reste constante.

Q5. Énoncer le premier principe de la thermodynamique en précisant le nom de chaque grandeur ainsi que leur unité.

On démontre que l’équation différentielle régissant l’évolution de la température en fonction du temps est donnée par :

$$\frac{dT}{dt}+\frac{T}{R_{\mathrm{contact}}\cdot C_{\mathrm{bolo}}}=\frac{P_{\mathrm{CMB}}}{C_{\mathrm{bolo}}}+\frac{T_T}{R_{\mathrm{contact}}\cdot C_{\mathrm{bolo}}}$$

Donnée :

• température du thermostat relié à la partie sensible : T_T = 0,1 K ;
• résistance thermique du matériau qui permet le contact entre la partie sensible du bolomètre et le thermostat : R_contact = 3,75×10⁹ K·W^–1 ;
• capacité thermique de la partie sensible du bolomètre : C_bolo = 0,40×10^–12 J·K^–1 ;
• dans le système international d’unités le Watt est équivalent à des Joules par secondes J·s^–1.

Q6.   Par   une   analyse   dimensionnelle,   montrer   que   la   quantité τ = R_contact⋅C_bolo est homogène à un temps, appelé temps caractéristique. Calculer sa valeur.

Q7. Sachant que la fonction $T(t) = T_T + T_1\cdot \left(1 – e^{-t/\tau}\right)$ est la solution de l’équation différentielle satisfaisant à la condition initiale T(0) = T_T, donner l’expression de T₁ ainsi que sa valeur.

On admet que le bolomètre réalise une mesure de puissance fiable, dès que sa température se stabilise, au bout d’une durée égale à 5 τ.

Afin d’étudier le CMB, le ciel est divisé en petites zones. Le satellite Planck balaie chaque zone pendant une durée Δt_scan = 14 ms.

Q8. Montrer que le bolomètre du satellite Planck peut obtenir une mesure fiable du CMB.