Bac Asie 2024 Sujet 2
Exercice 3 – (4 points) – Durée 0h42 – Calculatrice autorisée
Sujet n°24-PYCJ2JA1
Sujet et corrigé
Exercice 3 – Santé alimentaire – ne pas abuser des nitrites (4 points)
L’agence nationale de sécurité sanitaire de l’alimentation (ANSES) a confirmé que les nitrites ajoutés dans certaines viandes pour leur conservation (viandes « en salaison ») sont un facteur de risque d’apparition du cancer colorectal. Elle recommande d’en réduire l’usage, sans les interdire.
À l’échelle individuelle, la dose journalière admissible (DJA) établie par l’autorité européenne de sécurité des aliments (EFSA) sert de repère pour permettre à chacun de réguler sa consommation et ainsi limiter les risques. Le principe d’une DJA est d’évaluer la quantité maximale d’un composé qu’un individu peut consommer quotidiennement toute sa vie sans risque pour sa santé. C’est une quantité exprimée en milligramme de composé par kilogramme de masse corporelle.
Donnée :
- Pour les nitrites, la DJA est de 0,07 mg par kilogramme de masse corporelle.
Dans cet exercice, on souhaite déterminer la quantité de nitrite contenue dans une tranche de viande en salaison et estimer combien de tranches peut manger une personne de 70 kg dans une journée en respectant la DJA.
Mode opératoire : dosage par spectrophotométrie
Pour déterminer la quantité d’ions nitrite présents dans une tranche de viande en salaison, on procède dans un premier temps à un traitement d’extraction de ces ions, non détaillé ici, suivi de leur mise en solution.
On souhaite alors procéder au dosage de ces ions par spectrophotométrie. Toutefois, les ions nitrite sont incolores en solution. Pour résoudre cette difficulté, on utilise le « réactif de Griess », une espèce chimique avec laquelle les ions nitrite interagissent de manière totale
pour former une nouvelle entité colorée. Le document 1 présente le spectre d’absorption de la solution après ajout du réactif de Griess.
Q1- Déterminer, en justifiant, la couleur de la solution ainsi obtenue.
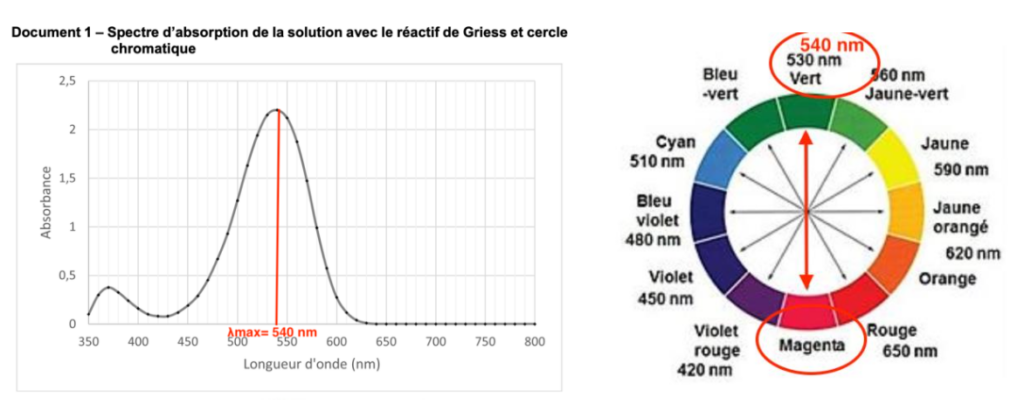
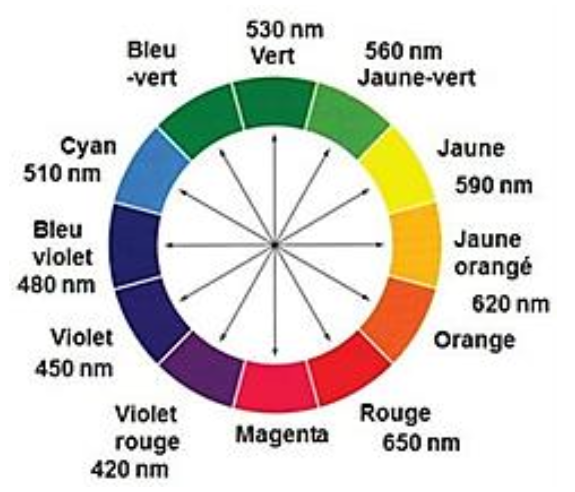
La couleur absorbée correspond à λmax=540 nm : couleur vert.
Sa couleur est la couleur complémentaire du vert (couleur opposée sur le cercle chromatique) : le magenta. La solution est donc de couleur magenta.
Q2- Préciser, en justifiant, la longueur d’onde à laquelle régler le spectrophotomètre pour réaliser les mesures d’absorbance.
La longueur d’onde à laquelle il faut régler le spectrophotomètre pour réaliser les mesures d’absorbance est λmax=540 nm.
Document 1 – Spectre d’absorption de la solution avec le réactif de Griess et cercle chromatique
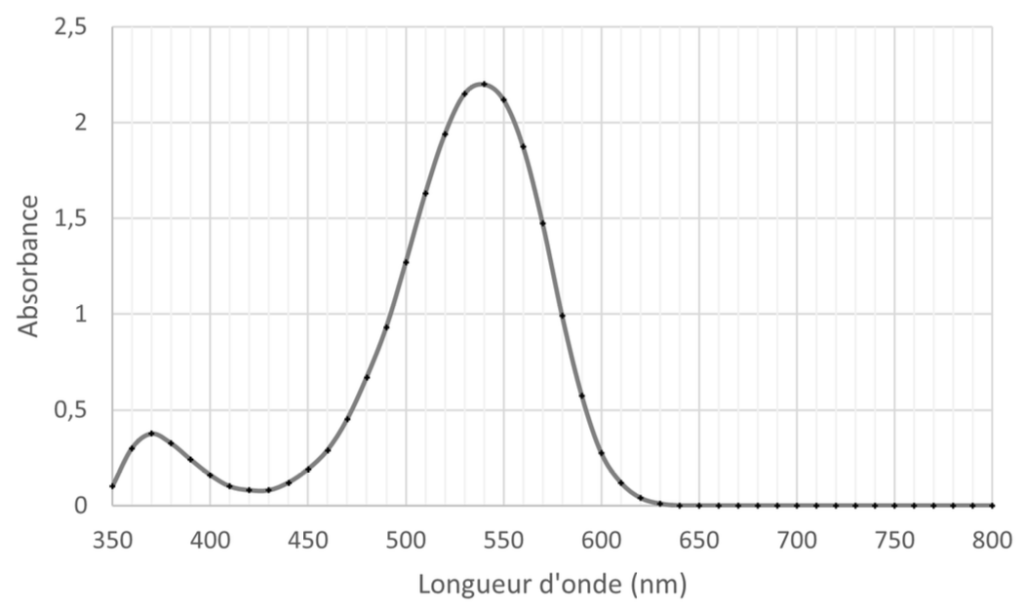
Pour tracer la courbe d’étalonnage, cinq solutions étalons sont préparées à partir d’une solution mère S0 ayant une concentration en ions nitrite : 𝑐0 = 3,0 × 10−3 mol ⋅ L−1. Les concentrations 𝑐f des solutions étalons sont indiquées dans le tableau ci-après.
| Solution | S1 | S2 | S3 | S4 | S5 |
| 𝑐f (mol ⋅ L−1) | 60 × 10−6 | 100 × 10−6 | 150 × 10−6 | 250 × 10−6 | 300 × 10−6 |
Le préparateur dispose de la verrerie suivante :
- Béchers : 50 mL ; 100 mL ; 250 mL.
- Éprouvettes graduées : 50 mL ; 100 mL ; 250 mL.
- Fioles jaugées : 50 mL ; 100 mL ; 250 mL.
- Pipettes jaugées : 5,0 mL ; 10,0 mL ; 20,0 mL.
Q3- Présenter la démarche expérimentale à mettre en œuvre pour préparer la solution étalon S1 en indiquant la verrerie à utiliser (dans la liste ci-dessus).
Calculons le facteur de dilution :
$$F=\frac{C_0}{C_1}$$
$$F=\frac{3,0\times{10}^{-3}}{60\times{10}^{-6}}$$
$$F=50$$
Or
$$F=\frac{V_1}{V_0}$$
$$\frac{V_1}{V_0}=F$$
$$V_1=F\times V_0$$
$$V_1=50\times V_0$$
Il faut choisir une fiole jaugée d’un volume 50 fois plus grand que celui de la pipette jaugée.
On choisit la pipette jaugée de 5,0 mL et la fiole jaugée de 250 mL.

Protocole de la dilution :
- Prendre une fiole jaugée de 250 mL.
- Ajouter à l’aide d’une pipette jaugée le volume V=5,0 de la solution mère à prélever dans la fiole jaugée.
- Ajouter au ¾ de l’eau distillée. Agiter.
- Ajuster avec de l’eau distillée jusqu’au trait de jauge.
- Homogénéiser
On ajoute le réactif de Griess à chaque solution pour obtenir la coloration. On homogénéise pendant dix minutes puis on mesure l’absorbance 𝐴 des solutions à la longueur d’onde déterminée à la question Q2. Les points de mesure sont rassemblés dans le document 2.
Q4- Justifier que les points obtenus sont compatibles avec la loi de Beer-Lambert.
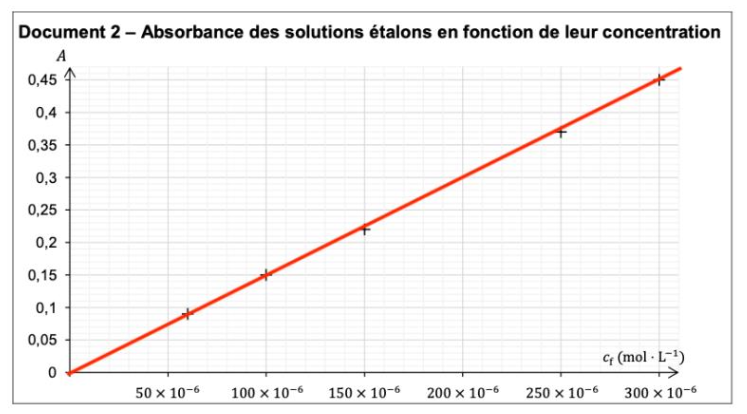
Document 2 – Absorbance des solutions étalons en fonction de leur concentration
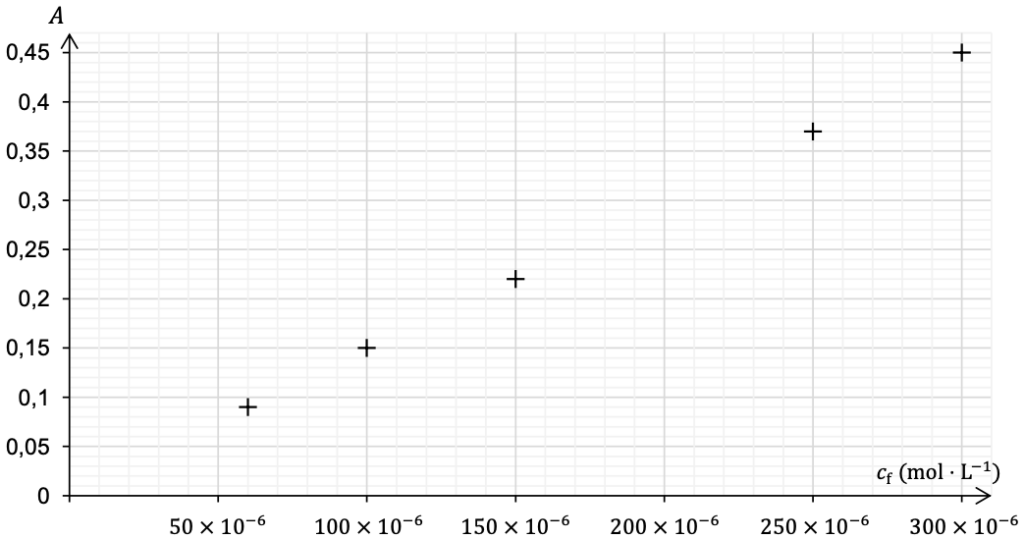
Le graphique est une droite passant par l’origine : A et C sont proportionnel ainsi A=KC.
La loi de Beer-Lambert est vérifié.
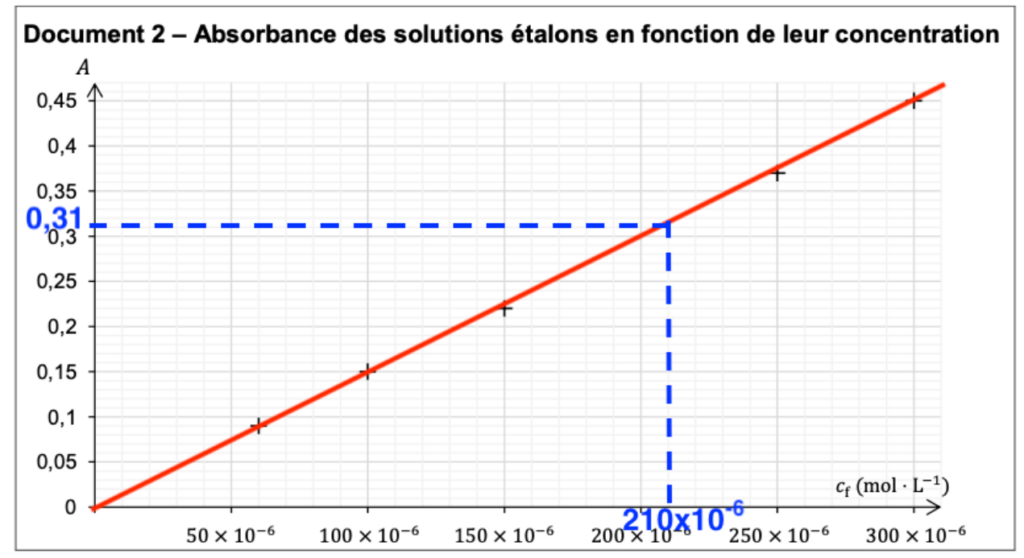
Le procédé d’extraction des ions nitrite de la tranche de viande en salaison a permis d’obtenir un volume 𝑉j = 50 mL d’une solution aqueuse Sj. On y ajoute le réactif de Griess et on procède à la mesure de l’absorbance dans les mêmes conditions que précédemment.
On mesure l’absorbance : 𝐴j = 0,31.
Q5- Déterminer la concentration en ions nitrite de la solution Sj.
Graphiquement, pour $A_j=0,31$ : $C=210\times{10}^{-6}\ \text{mol.L}^{-1}$
Combien peut-on manger de tranches ?
On souhaite déterminer combien de tranches de viande en salaison une personne de 70 kg
peut manger par jour en respectant la DJA. Hypothèses et données :
- Les tranches de viande en salaison sont supposées avoir toutes une masse et une teneur en nitrite proches de celles de la tranche étudiée précédemment.
- Masse molaire des ions nitrite : 𝑀(NO2−) = 46 g ⋅ mol−1.
- DJA des nitrites : 0,07 mg par kilogramme de masse corporelle.
- Masse corporelle de la personne considérée : 𝑚 = 70 kg.
Q6- Estimer la quantité de tranches de viande en salaison que la personne considérée peut manger par jour en respectant la DJA.
Dans cette question, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
Masse corporelle de la personne considérée : $m=70\ \text{kg}$.
DJA des nitrites : 0,07 mg par kilogramme de masse corporelle.
Calculons la masse de nitrite qu’une personne de 70 kg peut manger par jour en respectant la DJA.
| 0,07 mg | 1,0 Kg |
| $m_{max}$ | 70 Kg |
$$m_{max}=\frac{70\times0,07}{1,0}$$
$$m_{max}=4,9\ \text{mg}$$
$$m_{max}=4,9\times{10}^{-3}\ \text{g}$$
Calculons la masse de nitrite contenue dans une tranche :
$$n=\frac{m}{M}$$
$$\frac{m}{M}=n$$
$$m=n\times M$$
Or
$$c=\frac{n}{V}$$
$$\frac{n}{V}=c$$
$$n=c\times V$$
d’où
$$m=c\times V\times M$$
$$m=210\times{10}^{-6}\times50\times{10}^{-3}\times46$$
$$m=4,8\times{10}^{-4}\ \text{g}$$
Déterminons le nombre de tranches de viande en salaison que la personne considérée peut manger par jour en respectant la DJA.
| 1 tranche | $m=4,8\times{10}^{-4}\ \text{g}$ |
| N | $m_{max}=4,9\times{10}^{-3}\ \text{g}$ |
$$N=\frac{4,9\times{10}^{-3}\times1}{4,8\times{10}^{-4}}$$
$$N=10$$
Ainsi, une personne de 70 kg peut manger 10 tranches de tranches de viande en salaison par jour en respectant la DJA.
