Bac Amérique du Sud 2022 Sujet 1
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n°22-PYCJ1AS1
Sujet et corrigé
EXERCICE 1 commun à tous les candidats (10 points) SOLUTION DÉSINFECTANTE
Les autorités de santé rappellent qu’il est primordial de se laver régulièrement les mains avec de l’eau et du savon.
Toutefois, en l’absence de point d’eau, il est possible d’opter pour des gels ou solutions désinfectantes à la norme NF EN 14476.
On s’intéresse dans ce sujet à un désinfectant pour les mains ayant pour principe actif l’acide lactique en solution aqueuse.

Données :
- 100 g de solution désinfectante contient 1,75 g d’acide lactique ;
- masse molaire de l’acide lactique : 𝑀 = 90,1 g⋅mol−1 ;
- masse volumique de la solution désinfectante : 𝜌 = 1,00 g⋅mL−1 ;
- pH de la solution désinfectante : pH = 2,3.
- On considère que l’acide lactique est la seule espèce acide présente dans la solution désinfectante.
- conductivité ionique molaire à 25 °C :
- 𝜆(HO−) = 19,8 mS⋅m2⋅mol−1 ;
- 𝜆(Na+) = 5,01 mS⋅m2⋅mol−1 ;
- 𝜆(ion lactate) = 3,88 mS⋅m2⋅mol−1 ;
- incertitude-type sur la mesure d’une concentration 𝐶𝐴 donnée par la relation $C_A=\frac{C_B V_E}{V_A}$ :
$$\frac{u\left(C_A\right)}{C_A}=\sqrt{\left(\frac{u\left(V_A\right)}{V_A}\right)^2+\left(\frac{u\left(V_E\right)}{V_E}\right)^2+\left(\frac{u\left(C_B\right)}{C_B}\right)^2}$$
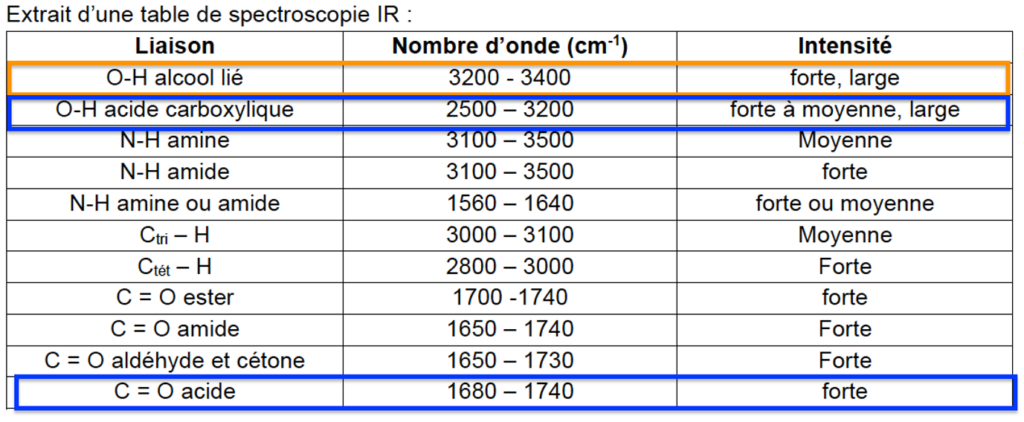
Extrait d’une table de spectroscopie IR :
| Liaison | Nombre d’onde (cm-1) | Intensité |
| O-H alcool lié | 3200 – 3400 | forte, large |
| O-H acide carboxylique | 2500 – 3200 | forte à moyenne, large |
| N-H amine | 3100 – 3500 | Moyenne |
| N-H amide | 3100 – 3500 | forte |
| N-H amine ou amide | 1560 – 1640 | forte ou moyenne |
| Ctri – H | 3000 – 3100 | Moyenne |
| Ctét – H | 2800 – 3000 | Forte |
| C = O ester | 1700 -1740 | forte |
| C = O amide | 1650 – 1740 | Forte |
| C = O aldéhyde et cétone | 1650 – 1730 | Forte |
| C = O acide | 1680 – 1740 | forte |
Partie A. Étude de l’acide lactique
L’autre nom de l’acide lactique est l’acide 2-hydroxypropanoïque. Sa formule développée est la suivante :
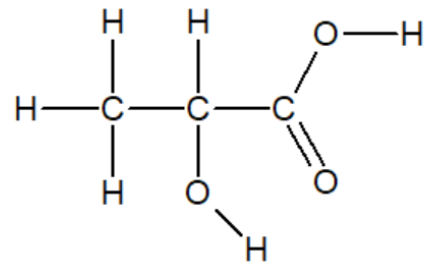
1. Établir le schéma de Lewis de la molécule d’acide lactique. Entourer et nommer ses groupes caractéristiques.
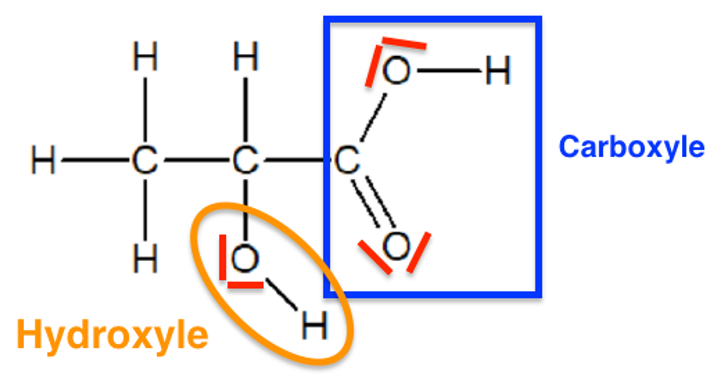
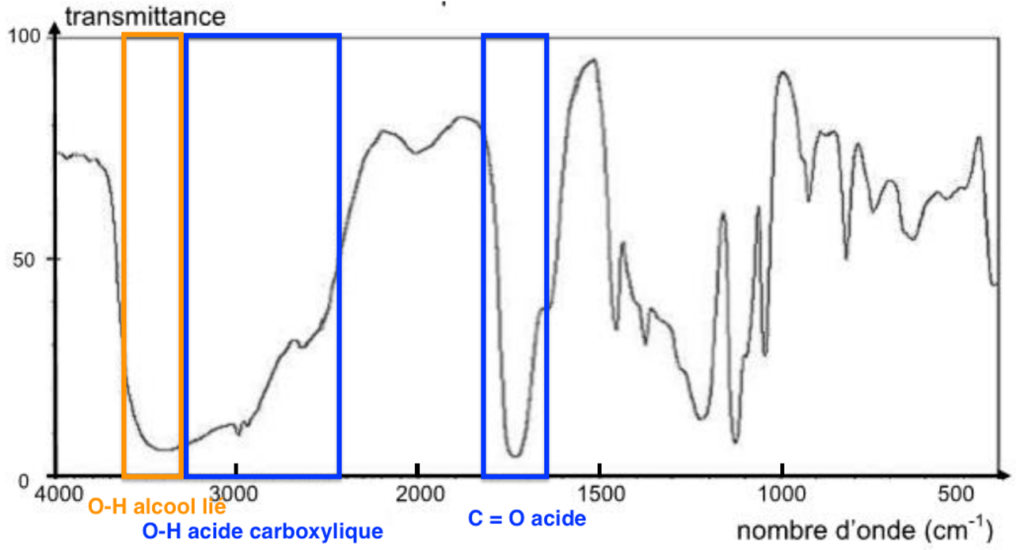
2. Le spectre IR de l’acide lactique est reproduit ci-dessous. Identifier deux bandes d’absorptions caractéristiques et repérer les liaisons correspondantes sur le schéma de Lewis de la molécule d’acide lactique.
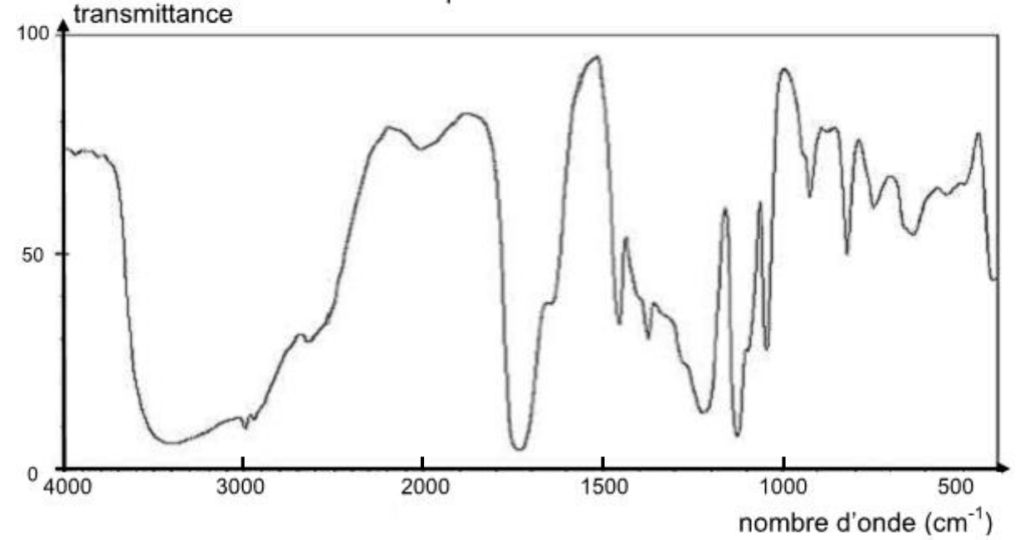
Figure 1. Spectre d’absorption IR de l’acide lactique
3. Vérifier que la valeur de la concentration en acide lactique apporté dans la solution désinfectante est voisine de 𝐶 = 0,20 mol⋅L−1.
D’après les données : « 100 g de solution désinfectante contient 1,75 g d’acide lactique »
$c_{acide\ lactique}=\frac{n_{acide\ lactique}}{V_{sol}}$
Or
$n_{acide\ lactique}=\frac{m_{acide\ lactique}}{M_{acide\ lactique}}$
Donc
$c_{acide\ lactique}=\frac{\frac{m_{acide\ lactique}}{M_{acide\ lactique}}}{V_{sol}}$
$c_{acide\ lactique}=\frac{m_{acide\ lactique}}{M_{acide\ lactique}\times V_{sol}}$
Or
$\rho_{sol}=\frac{m_{sol}}{V_{sol}}$
$V_{sol}=\frac{m_{sol}}{\rho_{sol}}$
Donc
$c_{acide\ lactique}=\frac{m_{acide\ lactique}}{M_{acide\ lactique}\times\frac{m_{sol}}{\rho_{sol}}}$
$c_{acide\ lactique}=\frac{m_{acide\ lactique}}{M_{acide\ lactique}}\times\frac{\rho_{sol}}{m_{sol}}$
$c_{acide\ lactique}=\frac{1,75}{90,1}\times\frac{1,00\times{10}^3}{100}$
$c_{acide\ lactique}=0,19\ mol.L^{-1}$
La valeur de la concentration en acide lactique apporté dans la solution désinfectante est voisine de $C=0,20\ mol\cdot L^{-1}$.
4. Rappeler la définition d’un acide de Brönsted.
Un Acide est une espèce capable de céder un proton H⁺.
5. Expliquer pourquoi, dans ces conditions, l’acide lactique est un acide faible. Un argument quantitatif est attendu.
Pour un acide fort $pH=-\log(c)$. Avec $c$ la concentration de l’acide fort.
$-\log(c)=-\log(0,20\ )$
$-\log(c)=0,70$
Or $pH=2,3$
$-\log(c)\neq pH$
L’acide lactique est donc un acide faible.
On note AH la molécule d’acide lactique pour la suite de l’exercice.
6. Écrire l’équation de la réaction modélisant la mise en solution aqueuse de cet acide.
$HA_{(aq)}+H_2O_{(l)}\rightleftarrows A^-{(aq)}+H_3O^+{(aq)}$
7. Compléter, sur l’annexe 1 à rendre avec la copie, le tableau d’avancement associé à cette transformation chimique à l’aide des notations de l’énoncé : 𝐶, 𝑝𝐻, 𝑉 et 𝑐𝑜, avec 𝑐𝑜 = 1 mol⋅L−1, concentration standard.
| Équation chimique | $HA_{(aq)}$ | $+H_2O_{(l)}$ | $ \rightarrow A^-{(aq)}$ | $+H_3O^+{(aq)}$ | |
| État du système | Avancement (mol) | Quantités de matière (mol) | |||
| État initial | $x=0$ | CV | ——— | 0 | 0 |
| État final | $x_f$ | $CV-x_f=CV-c^0\times{10}^{-pH}\times V$ | ——— | $x_f=c^0\times{10}^{-pH}\times V$ | $x_f=c^0\times{10}^{-pH}\times V$ |
$n_{AH}^i=CV$
$x_f=n_{H_3O^+}^f=\left[H_3O^+\right]_f\times V$
Or
$\left[H_3O^+\right]=c^0\times{10}^{-pH}$
Donc
$x_f=n_{H_3O^+}^f=c^0\times{10}^{-pH}\times V$
8. En utilisant la question précédente, exprimer la constante d’acidité K𝐴 du couple AH/A− en fonction des différentes concentrations à l’équilibre. En déduire la valeur de cette constante d’acidité. Commenter, sachant que la valeur de référence du pK𝐴 du couple acide lactique/ion lactate vaut 3,9.
$K_a=\frac{\left[A^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[HA\right]_{eq}\times c^0}$
$K_a=\frac{\frac{c^0\times{10}^{-pH}\times V}{V}\times\frac{c^0\times{10}^{-pH}\times V}{V}}{\frac{CV-c^0\times{10}^{-pH}\times V}{V}\times c^0}$
$K_a=\frac{c^0\times{10}^{-pH}\times c^0\times{10}^{-pH}}{\left(C-c^0\times{10}^{-pH}\right)\times c^0}$
$K_a=\frac{c^0\times{10}^{-2pH}}{C-c^0\times{10}^{-pH}}$
$K_a=\frac{1\times{10}^{-2\times2,3}}{0,20-1\times{10}^{-2,3}}$
$K_a=1,3\times{10}^{-4}$
$pK_a=-\log(K_a)$
$pK_a=-\log(1,3\times{10}^{-4})$
$pK_a=3,9$
La valeur trouvée correspond à la valeur de référence du $pK_a$ du couple acide lactique / ion lactate.
9. Un programme Python permet de tracer le diagramme de distribution du couple acide lactique/ion lactate noté AH/A−.
9.1. Établir, d’une part, la relation entre la concentration 𝐶 en acide lactique apporté, [𝐴𝐻]é𝑞 et [𝐴−]é𝑞 , et d’autre part la relation $pH=pK_A+log\left(\frac{\left[A^-\right]{eq}}{\left[AH\right]{eq}}\right)$
$\left[A^-\right]{eq}=c^0\times{10}^{-pH}$
$\left[HA\right]{eq}=C-c^0\times{10}^{-pH}$
Donc :
$C-c^0\times{10}^{-pH}=\left[HA\right]{eq}$
$C-\left[A^-\right]{eq}=\left[HA\right]{eq}$
$C=\left[HA\right]{eq}+\left[A^-\right]_{eq}$
$K_a=\frac{\left[A^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[HA\right]_{eq}\times c^0}$
$pK_a=-\log\left(\frac{\left[H_3O^+\right]{eq}}{c^0}\right)-\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}\right)$
$pK_a=pH-\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}\right)$
$pH=pK_a+\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]_{eq}}\right)$
9.2. À partir de ces deux relations, montrer que le pourcentage en acide AH, défini par $100\times\frac{\left[AH\right]_{eq}}{c}$, peut s’écrire $\frac{100}{1+10^{\left(pH-pK_A\right)}}$.
Pourcentage en acide AH, défini par $100\times\frac{\left[HA\right]_{eq}}{C}$
$C=\left[HA\right]{eq}+\left[A^-\right]{eq}$
$100\times\frac{\left[HA\right]{eq}}{C}=100\times\frac{\left[HA\right]{eq}}{\left[HA\right]{eq}+\left[A^-\right]{eq}}$
On divise le numérateur et le dénominateur par $\left[HA\right]_{eq}$ :
$100\times\frac{1}{1+\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}}$
Or
$pH=pK_a+\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}\right)$
$\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}\right)=pH-pK_a$
$\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}=10^{pH-pK_a}$
Donc
$100\times\frac{\left[HA\right]_{eq}}{C}=\frac{100}{1+10^{pH-pK_a}}$
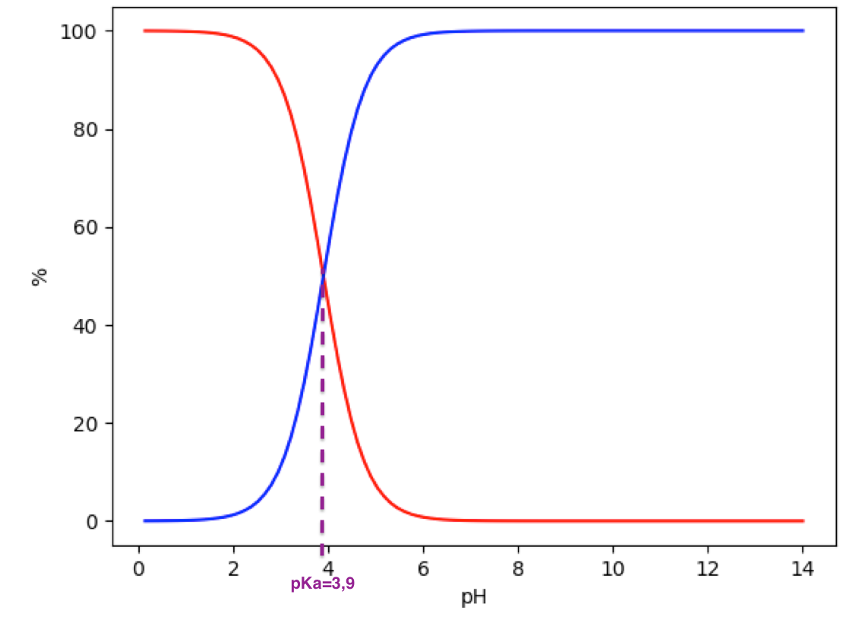
9.3. Un programme Python permet de tracer sur la figure 2 le diagramme de distribution du couple acide lactique/ion lactate noté AH/A−.
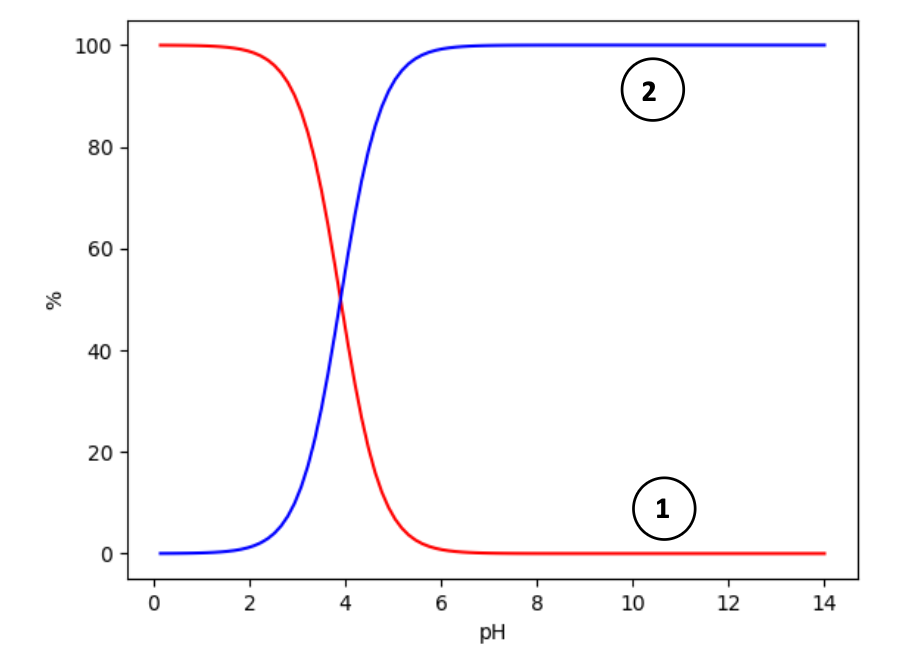
Figure 2. Diagramme de distribution du couple AH/A−
Indiquer à quelle espèce chimique correspond la courbe 1. Justifier. Expliquer comment il est possible de retrouver la valeur du pKA à partir d’une lecture graphique.
Le pourcentage en acide AH peut s’écrire :
$\frac{100}{1+10^{pH-pK_a}}$
Calculons lorsque le pH est nul :
$\frac{100}{1+10^{0-3,9}}=100$
Il y a 100 % d’acide AH lorsque le pH est nul. L’espèce chimique correspondant à la courbe 1 est l’acide AH.
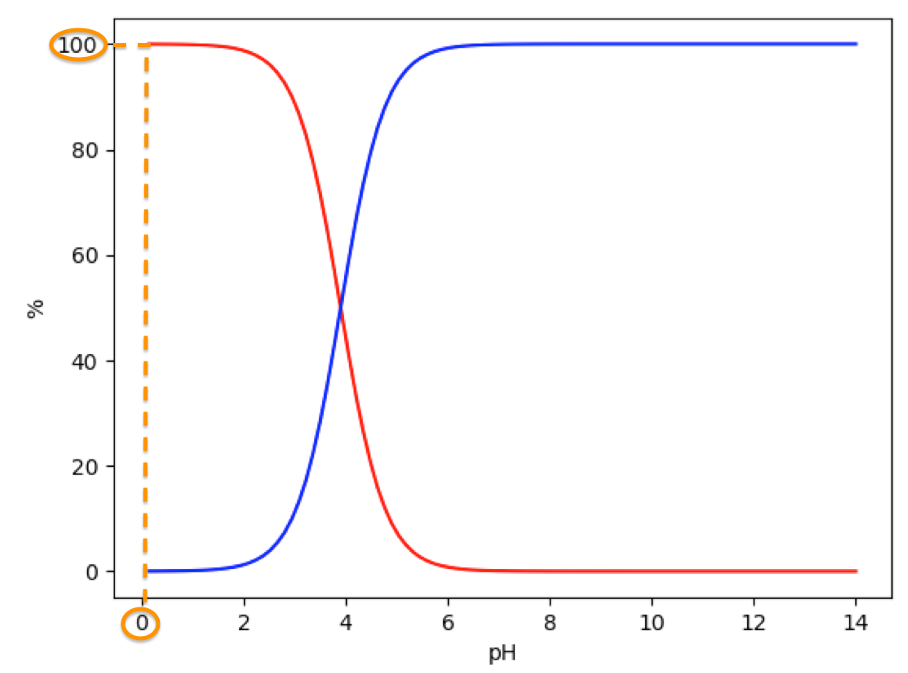
Méthode pour retrouver la valeur du $pK_a$ à partir d’une lecture graphique :
$pH=pK_a+\log\left(\frac{\left[A^-\right]{eq}}{\left[HA\right]{eq}}\right)$
Lorsque les courbes se croisent $\left[A^-\right]{eq}=\left[HA\right]{eq}$
Donc
$pH=pK_a+\log(1)$
$pH=pK_a$
La valeur du $pK_a$ est égale au pH lorsque les courbes se croisent.
Partie B. Titrage de l’acide lactique dans la solution désinfectante
Avant la commercialisation du produit, un laboratoire réalise un test de qualité sur sa solution désinfectante. Pour cela, un titrage acido-basique suivi par conductimétrie est réalisé après avoir dilué la solution désinfectante.
1. Proposer un protocole expérimental pour préparer 100,0 mL de solution désinfectante diluée 5 fois.
La solution S2 est obtenue par dilution d’un facteur cinq de la solution S1. Ainsi le volume V2 est 5 fois plus grand que V1.
Or on désire V2=100mL, on doit donc prendre V1=20mL
Protocole :
- Verser la solution mère dans un bécher
- Prélever à l’aide d’une pipette jaugée V1=20mL de la solution mère
- Introduire dans une fiole jaugée V2=100mL,
- Ajouter de l’eau distillée jusqu’au trait de jauge
- Homogénéiser la solution
Dans un bécher de 250 mL, on introduit un volume 𝑉𝐴 = 20,0 ± 0,05 mL de la solution désinfectante diluée. On ajoute 150 mL d’eau distillée. Le titrage est réalisé par une solution aqueuse d’hydroxyde de sodium de concentration en soluté apporté 𝐶𝐵 = (1,0 ± 0,1) × 10−1 mol⋅L−1. La courbe obtenue est donnée sur l’annexe 1 à rendre avec la copie.
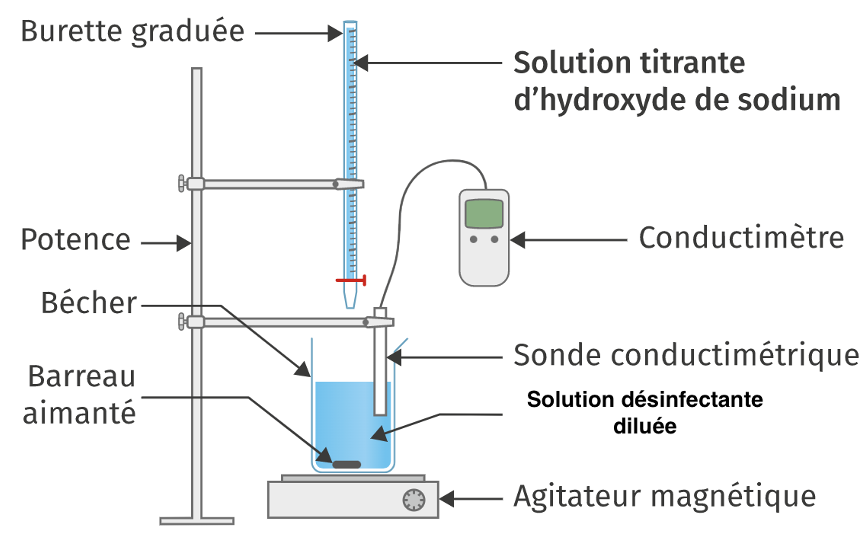
2. Schématiser et légender le dispositif de titrage sur la copie.
C’est un titrage par suivi conductimétrique.
3. Écrire l’équation de la réaction support du titrage.
Solution désinfectante AH
Hydroxyde de sodium $\left({\rm Na}^+ + {\rm HO}^-\right)$
Réaction acido-basique : ${\rm HO}^-$ réagit avec AH. ${\rm Na}^+$ est un ion spectateur.
Équation de la réaction support du titrage :
$AH_{(aq)}+{\rm HO}^-{(aq)}\rightarrow A^-{(aq)}+H_2O_{(l)}$
4. Interpréter qualitativement le changement de pente au voisinage de l’équivalence observé sur la courbe de titrage.
$AH_{(aq)}+{\rm HO}{(aq)}^-\rightarrow A{(aq)}^-+H_2O_{(l)}$
Avant l’équivalence :
$\left[A^-\right]$ augmente car c’est un produit de la réaction.
$\left[HO^-\right]$ est nulle car les ions $HO^-$ sont en défaut avant l’équivalence
$\left[{\rm Na}^+\right]$ augmente car les ions ${\rm Na}^+$sont spectateurs et ajoutés au cours du titrage.
| Ions | Avant l’équivalence |
| $\left[A^-\right]$ | ↗ |
| $\left[HO^-\right]$ | 0 |
| $\left[{\rm Na}^+\right]$ | ↗ |
Après l’équivalence :
$\left[A^-\right]$ reste car constant. $A^-$est un produit de la réaction or après l’équivalence, il n’y a plus de réaction entre $AH_{(aq)}$\ et\ ${\rm HO}_{(aq)}^-$ car tous les AH ont été consommés.
$\left[HO^-\right]$ augmente car les ions $HO^-$ sont en excès après l’équivalence et ils ne réagissent plus
$\left[{\rm Na}^+\right]$ augemente car les ions ${\rm Na}^+$sont spectateurs et ajoutés au cours du titrage.
| Ions | Après l’équivalence |
| $\left[A^-\right]$ | = |
| $\left[HO^-\right]$ | ↗ |
| $\left[HO^-\right]$ | ↗ |
Avant l’équivalence, la concentration des ions augmente donc la conductivité augmente.
Après l’équivalence, la concentration des ions augmente donc la conductivité augmente.
Comparons les deux augmentations :
$\lambda_{HO^-}>\lambda_{A^-}$ donc l’augmentation de la conductivité est plus importante après l’équivalence.
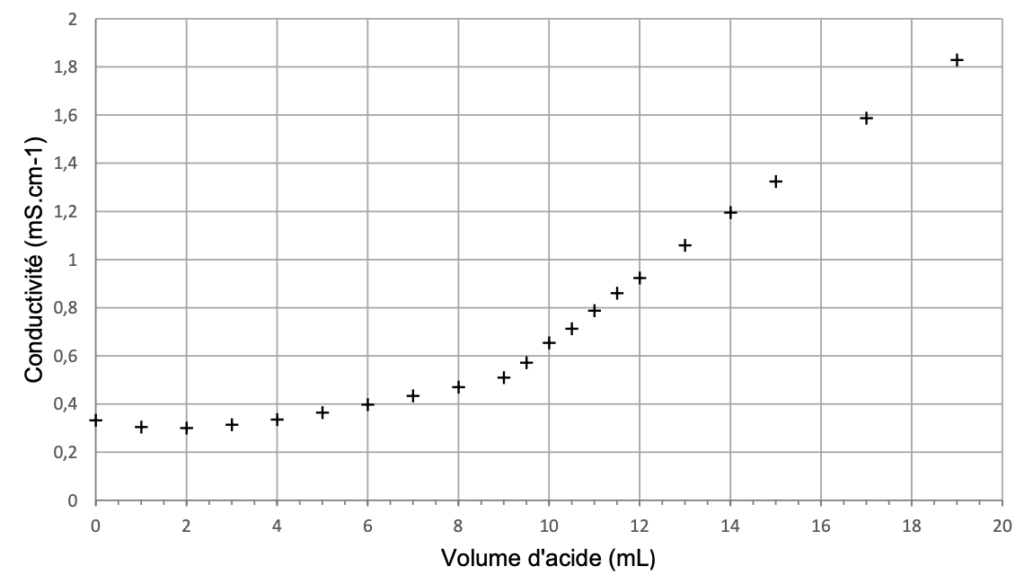
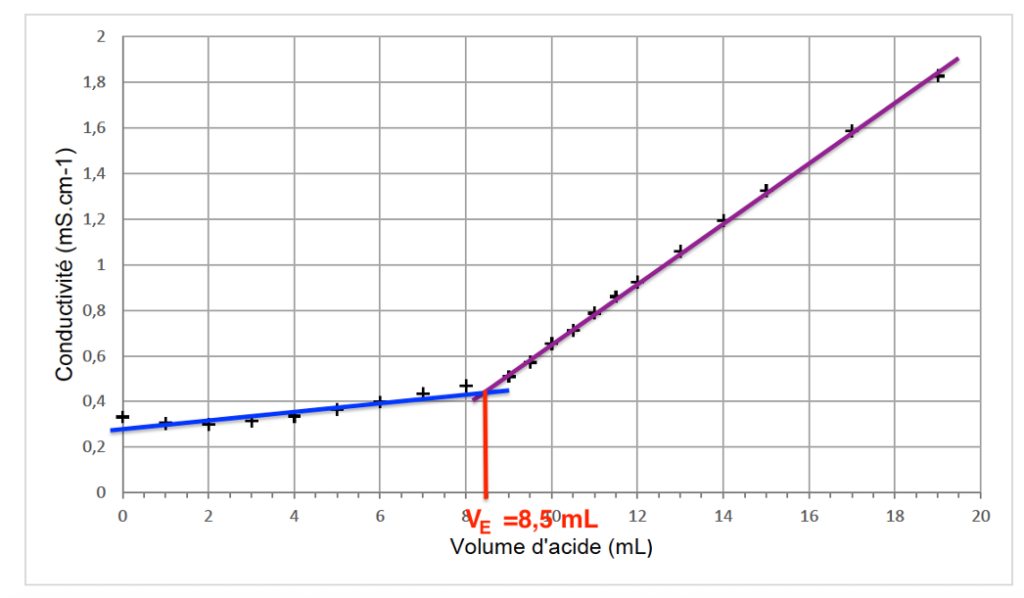
5. Déterminer graphiquement la valeur du volume à l’équivalence 𝑉𝐸 sur l’annexe 1 à rendre avec la copie.
La valeur du volume à l’équivalence VE se lit à l’intersection des deux droites : Graphiquement $V_E=8,5\ mL$.
On considère par la suite que l’incertitude-type sur 𝑉𝐸 est 𝑢(𝑉𝐸 ) = 0,1 mL.
6. Évaluer la concentration 𝐶 de la solution en acide lactique avant dilution. Évaluer l’incertitude- type sur la mesure sans prendre en compte la contribution liée à la dilution. Commenter.
À l’équivalence :
$\frac{n_{AH}^i}{1}=\frac{n_{HO^-}^{eq}}{1}$
$C_{A\ dilué}\times V_A=C_B\times V_E$
$C_{A\ dilué}=\frac{C_B\times V_E}{V_A}$
$C_{A\ dilué}=\frac{1,0\times{10}^{-1}\times8,5\times{10}^{-3}}{20,0\times{10}^{-3}}=4,3\times{10}^{-2}\ mol.L^{-1}$
Dilution par 5 :
$C_A=5\times C_{A\ dilué}$
$C_A=5\times4,3\times{10}^{-2}=0,22\ mol.L^{-1}$
Incertitude-type :
$\frac{u(C_A)}{C_A}=\sqrt{\left(\frac{u(V_A)}{V_A}\right)^2+\left(\frac{u(V_E)}{V_E}\right)^2+\left(\frac{u(C_B)}{C_B}\right)^2}$
$u(C_A)=C_A\times\sqrt{\left(\frac{u(V_A)}{V_A}\right)^2+\left(\frac{u(V_E)}{V_E}\right)^2+\left(\frac{u(C_B)}{C_B}\right)^2}$
$u(C_A)=0,22\times\sqrt{\left(\frac{0,05}{20,0}\right)^2+\left(\frac{0,1}{8,5}\right)^2+\left(\frac{0,1}{1,0}\right)^2}$
$u(C_A)=0,03$
$C_A=0,22\pm0,03\ mol.L^{-1}$
$0,19\ mol.L^{-1}<C_A<0,25\ mol.L^{-1}$
La valeur attendue $c_{acide\ lactique}=0,20\ mol.L^{-1}$ est comprise dans cet intervalle : les deux valeurs sont en accord.
ANNEXE 1 À RENDRE AVEC LA COPIE
Exercice 1, partie A, question 7. Tableau d’avancement
| Équation chimique | $+H_2O_{(l)}$ | ||||
| État du système | Avancement (mol) | Quantités de matière (mol) | |||
| État initial | $x=0$ | ——— | |||
| État final | $x_f$ | ——— | |||
Exercice 1, partie B, question 5. Titrage par suivi conductimétrique d’une solution diluée d’acide lactique