Suivi cinétique d’une décoloration

Bac Métropole Septembre 2024 Sujet 2

Exercice 3 – (5 points) – Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ2ME3

Exercice 3 – Suivi cinétique d’une décoloration (5 points)

La phénolphtaléine est une substance utilisée en chimie pour ses propriétés colorantes et acido-basiques. Elle est souvent choisie comme indicateur de pH, notamment pour repérer l’équivalence de certains titrages.

Les espèces associées à la phénolphtaléine en solution aqueuse sont représentées ci-dessous :

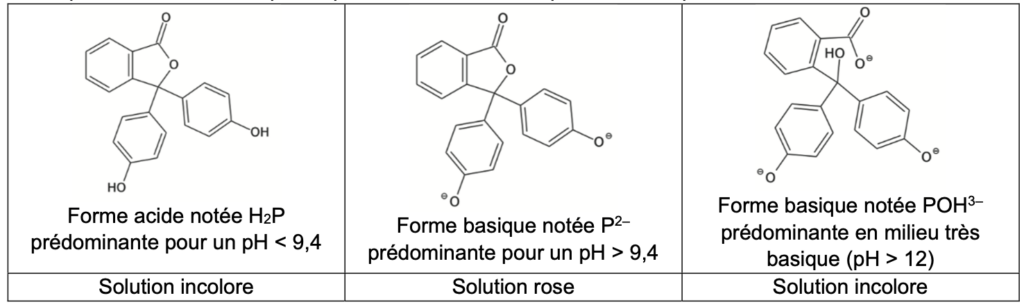
Les transformations mettant en jeu les espèces H2P et P^2– étant instantanées, la phénolphtaléine est utilisée pour distinguer un milieu basique (rose) d’un milieu acide (incolore).

Mis en milieu très basique (pH > 12), les ions P^2– réagissent lentement avec les ions hydroxyde OH^– pour former des ions POH^3– selon l’équation ci-après. Cette réaction s’accompagne d’une décoloration progressive de la solution rose de phénolphtaléine, ce qui peut être potentiellement gênant lors des titrages.

P^2–(aq) + OH^–(aq) → POH^3–(aq)

L’objectif de cet exercice est d’étudier la cinétique de la réaction associée à cette décoloration en milieu très basique.

Données :

produit ionique de l’eau à 25°C : K_e = 1,0×10⁻¹⁴ ;
concentration standard : c° = 1,0 mol·L^–1 ;
ci-contre, pictogramme de sécurité de la phénolphtaléine sous forme solide ou en solution de concentration supérieure à 3×10^–2 mol·L^–1.

Protocole du suivi cinétique de la décoloration ;

dans un bécher, introduire 30 mL d’une solution aqueuse d’hydroxyde de sodium de concentration C = 0,50 mol·L^–1 ;
déclencher le chronomètre (instant t = 0) lorsque l’on introduit dans le bécher 0,50 mL d’une solution basique de phénolphtaléine de concentration en ions P^2– égale à 1,6×10^–3 mol·L^–1 ;
mélanger rapidement, transvaser dans une cuve spectrophotométrique. Relever l’absorbance du milieu à une longueur d’onde appropriée toutes les 10 secondes pendant quinze minutes.

Dans cette expérience, on considère que les ions hydroxyde OH^– apportés par la solution d’hydroxyde de sodium sont en large excès par rapport aux ions P^2–. On considère que leur concentration reste constante pendant toute la durée de l’expérience :

[OH^–](t) = C = 0,50 mol·L^–1.

1. Étude des conditions initiales

Q1. Préciser la signification du pictogramme de sécurité associé à la phénolphtaléine. Justifier l’un des critères de choix des conditions expérimentales.

Le pictogramme de sécurité associé à la phénolphtaléine désigne un produit cancérogène.

La solution de phénolphtaléine est de concentration égale à 1,6×10^–3 mol·L^–1 ;

Cette concentration est inférieure à 1,6×10^–3 mol·L^–1 (concentration à partir de laquelle le pictogramme est indiquée sur la solution)

Q2. Estimer la valeur du pH de la solution aqueuse d’hydroxyde de sodium utilisée dans l’expérience. Commenter.

$pH=-log\left(\frac{\left[H_3O^+\right]}{c^0}\right)$

Or
$K_e=\frac{\left[H_3O^+\right]{eq}\times\left[{\rm HO}^-\right]{eq}}{{{(c}^0)}^2}$
$\frac{\left[H_3O^+\right]{eq}\times\left[{\rm HO}^-\right]{eq}}{{{(c}^0)}^2}=K_e$
$\left[H_3O^+\right]{eq}=\frac{K_e\times{{(c}^0)}^2}{\left[{\rm HO}^-\right]{eq}}$

D’ou
$pH=-log\left(\frac{\frac{K_e\times{{(c}^0)}^2}{\left[{\rm HO}^-\right]{eq}}}{c^0}\right)$
$pH=-log\left(\frac{K_e\times c^0}{\left[{\rm HO}^-\right]{eq}}\right)$
$pH=-log\left(\frac{1,0\times{10}^{-14}\times 1,0}{0,50}\right)$
$pH=14$

Q3. Montrer que, une fois que la solution de phénolphtaléine a été introduite dans la solution d’hydroxyde de sodium à la date t = 0, la concentration des ions P^2– est [P²⁻]₀ = 2,6×10⁻⁵ mol·L⁻¹.

Dans le bécher on introduit 0,50 mL d’une solution basique de phénolphtaléine de concentration en ions P^2– égale à 1,6×10^–3 mol·L^–1 ;

Dans ce meme bécher, on introduit 30 mL d’une solution aqueuse d’hydroxyde de sodium de concentration C = 0,50 mol·L^–1 ;

On cherche la concentration des ions P^2– dans ce mélange

$\left[P^{2-}\right]0=\frac{n_{P^{2-}}}{V_{Sol}}$

Or
$\left[P^{2-}\right]{introduite}=\frac{n_{P^{2-}}}{V_1}$
$\frac{n_{P^{2-}}}{V_1}=\left[P^{2-}\right]{introduite}$
$n_{P^{2-}}=\left[P^{2-}\right]_{introduite}\times V_1$

D’où
$\left[P^{2-}\right]0=\frac{\left[P^{2-}\right]{introduite}\times V_1}{V_{Sol}}$

Or
$V_{Sol}=V_1+V_2$

D’où
$\left[P^{2-}\right]0=\frac{\left[P^{2-}\right]{introduite}\times V_1}{V_1+V_2}$
$\left[P^{2-}\right]_0=\frac{1,6\times{10}^{-3}\times 0,50}{0,50+30}$
$\left[P^{2-}\right]_0=2,6\times{10}^{-5}\ mol\cdot L^{-1}$

2. Étude cinétique de la décoloration

Les résultats expérimentaux permettent de tracer l’évolution de la vitesse de disparition de l’ion P^2– en fonction de sa concentration (figure 1).

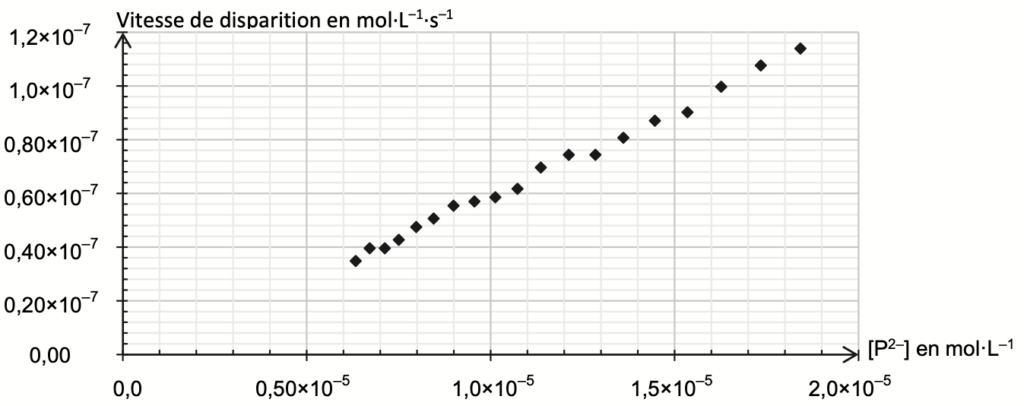
Figure 1. Évolution de la vitesse de disparition de la forme P^2– en fonction de la concentration en P^2– On fait l’hypothèse que l’évolution de la concentration suit une loi de vitesse d’ordre 1.

Q4. Expliquer en quoi les résultats expérimentaux donnés en figure 1 sont compatibles avec cette hypothèse. Dans ce cadre, la concentration en ions P^2– à l’instant t, notée [P^2–](t), est régie par l’équation différentielle :
$$ \frac{d [P^{2-}](t)}{dt}=-k\cdot [P^{2-}](t) $$

Lorsque l’évolution de la concentration suit une loi de vitesse d’ordre 1, la vitesse est proportionnelle à la concentration : v=kc

Les résultats expérimentaux donnés en figure 1 montrent une droite passant par l’origine : la vitesse de disparition v et la concentration$\left[P^{2-}\right]$ sont proportionnel : $v=k\times\left[P^{2-}\right]$

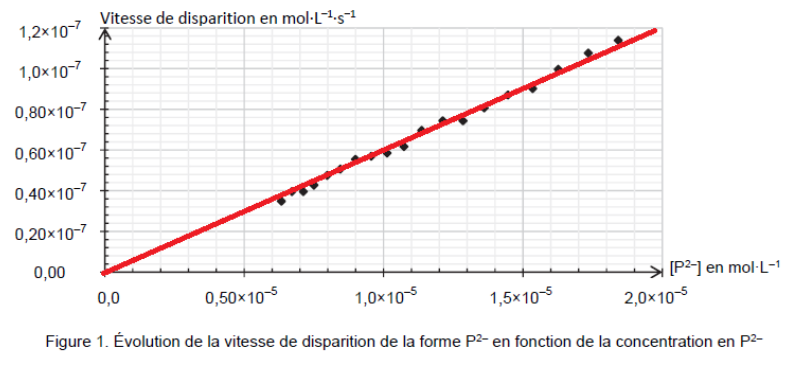
Ainsi, les résultats expérimentaux donnés en figure 1 sont compatibles avec l’hypothèse que l’évolution de la concentration suit une loi de vitesse d’ordre 1.

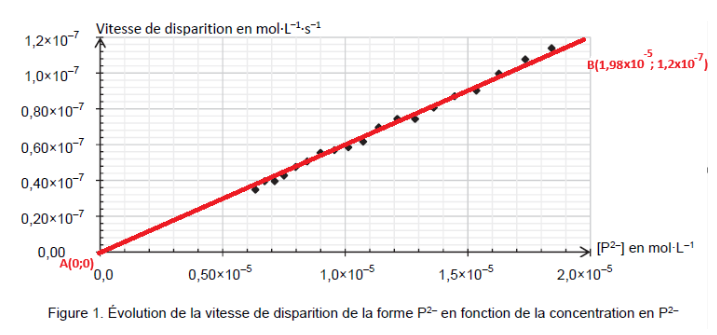
Q5. Déterminer le coefficient k à l’aide du graphique de la figure 1.

Le coefficient k est le coefficient directeur de la courbe :
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{1,2\times{10}^{-7}-0}{1,98\times{10}^{-5}-0}$
$k=6,0\times{10}^{-3}\ s^{-1}$

La figure 2 de L’ANNEXE À RENDRE AVEC LA COPIE présente l’évolution temporelle de la concentration de la forme P^2– de la phénolphtaléine.

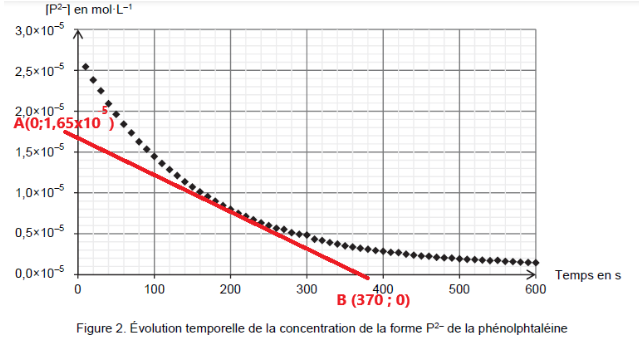
Q6. Déterminer, à l’aide de la figure 2 de L’ANNEXE À RENDRE AVEC LA COPIE, la valeur de la vitesse volumique de disparition vd de la forme P^2– de la phénolphtaléine à la date t = 200 s. On fera apparaître la construction effectuée sur le graphique.

$v_d=-\frac{d\left[P^{2-}\right]_{(t)}}{dt}$

La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.

Par exemple pour t=200s :
$k=\frac{y_B-y_A}{x_B-x_A}$
$k=\frac{0-1,65\times{10}^{-5}}{370-0}=-4,5.{10}^{-8}mol.L^{-1}.s^{-1}$
$v_{t=200s}=-\frac{d\left[P^{2-}\right]{(t)}}{dt}=-k$
$v{t=200s}=4,5.{10}^{-8}mol.L^{-1}.s^{-1}$

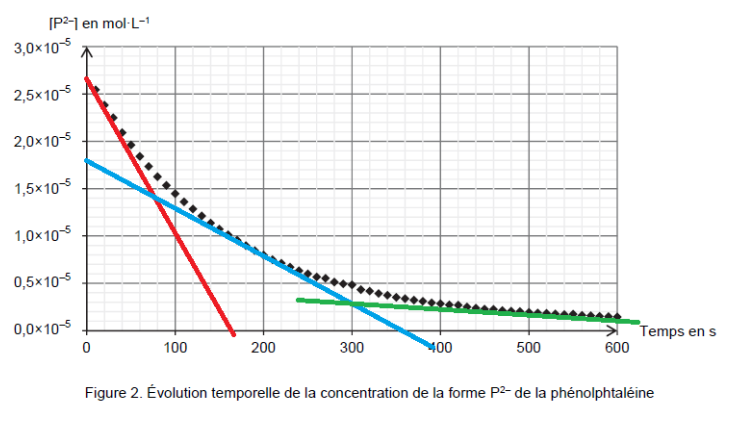
Q7. Indiquer, en justifiant la réponse, l’évolution de cette vitesse au cours du temps.

$v=-\frac{d\left[P^{2-}\right]_{(t)}}{dt}=-k$
Au cours du temps, la valeur absolue du coefficient directeur de la tangente en un point de la courbe diminue.
Ainsi, la vitesse de disparition diminue au cours du temps.

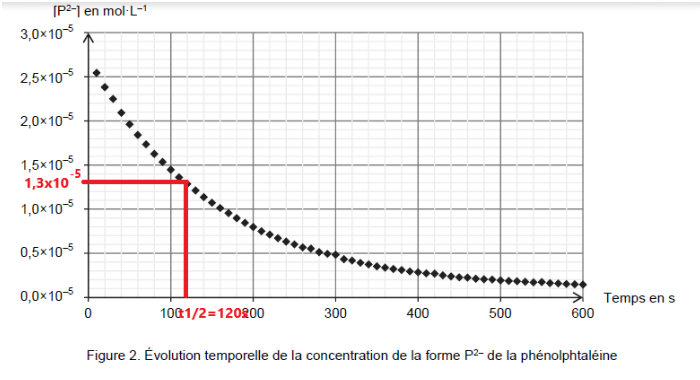
Q8. Définir le temps de demi-réaction t_1/2 et estimer sa valeur dans le cas de cette transformation chimique, considérée totale.

t_1/2 est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : x(t_1/2 ) = xf/2.
$\left[P^{2-}\right]{\left(t=t{1/2}\right)}=\frac{\left[P^{2-}\right]0}{2}$
$\left[P^{2-}\right]{\left(t=t_{1/2}\right)}=\frac{2,6\times{10}^{-5}}{2}$
$\left[P^{2-}\right]{\left(t=t{1/2}\right)}=1,3\times{10}^{-5}\ mol\cdot L^{-1}$

Graphiquement, pour
$\left[P^{2-}\right]{\left(t=t{1/2}\right)}=1,3\times{10}^{-5}\ mol\cdot L^{-1}$ on lit t1/2 =120 s

La concentration en ions P^2– de la phénolphtaléine suit la loi d’équation : [P^2–](t)=[P^2–]₀ · e⁻^k∙t, où k correspond à la constante déterminée à la question Q5.

Q9. Déterminer la relation entre k et t_1/2.

$\left[P^{2-}\right]_{\left(t\right)}=\left[P^{2-}\right]_0{\times e}^{-k\times t}$

Ainsi :
$\left[P^{2-}\right]{\left(t=t{1/2}\right)}=\left[P^{2-}\right]0{\times e}^{-k\times t{1/2}}$
$\left[P^{2-}\right]0{\times e}^{-k\times t{1/2}}=\left[P^{2-}\right]{\left(t=t{1/2}\right)}$
Or
$\left[P^{2-}\right]{\left(t=t{1/2}\right)}=\frac{\left[P^{2-}\right]_0}{2}$

Donc
$\left[P^{2-}\right]0{\times e}^{-k\times t{1/2}}\ =\frac{\left[P^{2-}\right]0}{2}$
$e^{-k\times t{1/2}}=\frac{1}{2}$
$ln\left(e^{-k\times t_{1/2}}\right)=ln\left(\frac{1}{2}\right)$
$-k\times t_{1/2}=-\ln\left(2\right)$
$t_{1/2}=\frac{\ln{\left(2\right)}}{k}$

Q10. Comparer la valeur de t_1/2 obtenue avec cette relation avec la valeur trouvée à la question Q8. Commenter.

Calculons t_1/2 :
$t_{1/2}=\frac{\ln{\left(2\right)}}{k}$
$t_{1/2}=\frac{\ln{\left(2\right)}}{6,0\times{10}^{-3}}$
$t_{1/2}=116\ s$

La valeur de t_1/2 calculée et celle mesurée (t_1/2 =120 s) à la question Q8 sont semblables.

Ainsi, l’hypothèse que l’évolution de la concentration suit une loi de vitesse d’ordre 1 est vérifiée.

Q11. Commenter la valeur de t_1/2 obtenue au regard de l’utilisation de la phénolphtaléine comme indicateur coloré de certains titrages de solutions acides.

t_1/2 =120 s : la réaction est lente (la concentration diminue de moitié toute les 120s soit 2 minutes).
La décoloration des ions P^2– est lente. La couleur permettant de repérer l’équivalence est persistante.
La décoloration progressive de la solution rose de phénolphtaléine, n’est pas gênante lors des titrages.
Ainsi, la phénolphtaléine peut servir à un dosage par titrage.
Attention : au bout d’un temps correspondant à 5 fois t_1/2 soit 10 min, la coloration aura disparu.

ANNEXE À RENDRE AVEC LA COPIE

Figure 2. Évolution temporelle de la concentration de la forme P^2– de la phénolphtaléine