Suivi cinétique par conductimétrie de l’hydrolyse du chlorure de tertiobutyle

Bac Polynésie 2024 Sujet 2

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°24-PYCJ2PO1

EXERCICE 1 – SUIVI CINÉTIQUE PAR CONDUCTIMÉTRIE DE L’HYDROLYSE DU CHLORURE DE TERTIOBUTYLE (9 POINTS)

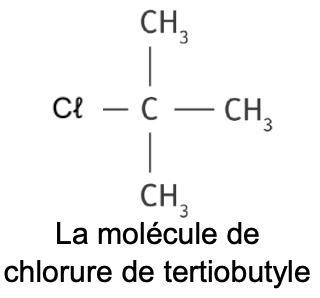
L’objectif de cet exercice est de suivre l’évolution temporelle de l’hydrolyse du chlorure de tertiobutyle.

Suivi conductimétrique de l’hydrolyse du chlorure de tertiobutyle.

Lorsqu’une transformation chimique lente met en jeu une espèce ionique, la conductimétrie permet d’étudier sa cinétique.

Données :

• Le chlorure de tertiobutyle a pour formule (CH₃)₃C-Cℓ. Pour simplifier, il sera noté par la suite RCℓ où le groupe alkyle R représente (CH₃)₃C- ;
• L’équation de la réaction modélisant l’hydrolyse du chlorure de tertiobutyle est :
  • RCℓ(aq) + 2 H2O(ℓ) → ROH(aq) + H₃O⁺(aq) + Cℓ^– (aq)
• La valeur de la masse volumique ρ du chlorure de tertiobutyle : ρ = 0,850 g·mL^–1 ;
• Tableau regroupant les masses molaires atomiques des atomes de carbone, d’hydrogène et de chlore :

Atomes	Carbone C	Hydrogène H	Chlore Cℓ
Masses molaires en g·mol–1	12,0	1,00	35,5

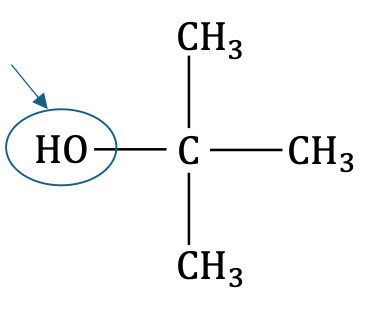
Q1. Représenter la formule semi-développée de l’alcool ROH produit lors de l’hydrolyse du chlorure de tertiobutyle. Entourer et nommer le groupe caractéristique présent.

Pour réaliser l’étude cinétique de l’hydrolyse du chlorure de tertiobutyle, on met en œuvre le protocole suivant :

• Verser un volume V_e = 200 mL d’un mélange d’eau et de propanone dans un bécher ;
• Placer le bécher dans un cristallisoir rempli d’eau ;
• Installer une sonde conductimétrique et un dispositif d’agitation ;
• À l’aide d’une pipette jaugée, verser un volume V = 1,0 mL de chlorure de tertiobutyle dans le volume Ve et déclencher l’enregistrement à cet instant ;
• Mesurer la conductivité σ toutes les 5 minutes pendant environ 100 minutes en prenant soin de stopper l’agitation pendant les mesures.

La courbe représentant la variation de la conductivité σ en fonction du temps t est donnée figure 1.

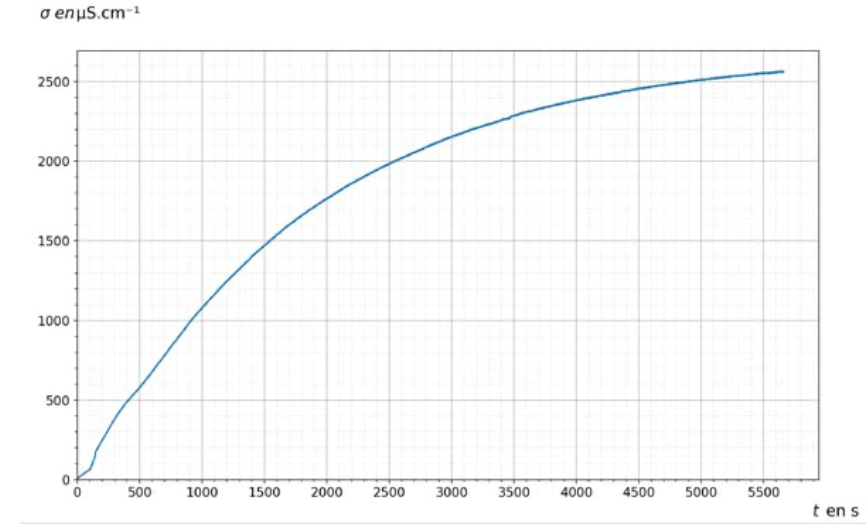
Figure 1. Représentation graphique des variations de la conductivité σ de la solution en fonction du temps t.

Donnée :

• Loi de Kohlrausch donne, pour une solution diluée, l’expression de la conductivité σ :

$$\sigma=\sum_{i=1}^{n}\lambda_i\cdot [X_i]$$

avec λ_i la conductivité molaire ionique de l’ion X_i et [X_i ] la concentration en quantité de matière de l’ion X_i .

Q2. À partir de la loi de Kohlrausch, exprimer la conductivité σ de la solution en fonction des concentrations en quantité de matière en ions oxonium H₃O⁺ et en ions chlorure Cℓ– respectivement notées [H₃O⁺] et [Cℓ^–] et des conductivités molaires ioniques de chaque ion notées λ_H3O⁺ et λ_Cℓ–.

D’après la loi de Kohlrausch, la conductivité de la solution s’exprime par :
$$\sigma=\left[{H_3O}^+\right]\times\lambda_{{H_3O}^+}+[{\rm Cl}^-]\times \lambda Cl^-$$

Q3. En déduire une expression de σ en fonction de la concentration en quantité de matière en ions oxonium [H₃O⁺] et des conductivités molaires ioniques λ_H3O⁺ et λ_Cℓ–.

Or, à l’état finale de la réaction, $n_{{H_3O}^+}=n_{{Cl}^-}$ (par proportions stœchiométriques).
Donc $\frac{n_{{H_3O}^+}}{V}=\frac{n_{{Cl}^-}}{V}$, et $\left[{H_3O}^+\right]=\left[{Cl}^-\right]$
$$\sigma=\left[{H_3O}^+\right]\times\lambda_{{H_3O}^+}+\left[{\rm Cl}^-\right]\times\lambda_{{\rm Cl}^-}=\left[{H_3O}^+\right]\times\lambda_{{H_3O}^+}+\left[{H_3O}^+\right]\times\lambda_{{\rm Cl}^-}$$
$$\sigma=\left[{H_3O}^+\right]\times\left(\lambda_{{H_3O}^+}+\lambda_{{\rm Cl}^-}\right)$$

Q4. À partir de l’expression établie à la question précédente, justifier qu’il est possible de réaliser un suivi cinétique par conductimétrie de l’hydrolyse du chlorure de tertiobutyle.

D’après l’équation de réaction : $${RCl}{(aq)}+2\ {H_2O}{(l)}\longrightarrow{ROH}{\left(aq\right)}+{{H_3O}^+}{\left(aq\right)}+{{Cl}^-}{\left(aq\right)}$$
${H_3O}^+$ est un produit. Donc, au cours de la réaction, la concentration $\left[{H_3O}^+\right]$ augmente.
Or d’après la relation $\sigma=\left[{H_3O}^+\right]\times\left(\lambda{{H_3O}^+}+\lambda_{{\rm Cl}^-}\right)$, la conductivité de la solution varie en fonction de $\left[{H_3O}^+\right]$, et $\sigma$ va augmenter aussi. Il est donc possible de réaliser un suivi cinétique par conductimétrie de l’hydrolyse du chlorure de tertiobutyle.

Q5. Calculer la valeur de la quantité de matière initiale de chlorure de tertiobutyle introduit notée n₀.

Formules : $n=\frac{m}{M}$ et $\rho=\frac{m}{V}$ donc $m=\rho\times V$
D’après l’énoncé : $\rho=0,850\ g/mL$ et $V=1,0\ mL$
$$M_{{({CH}3)}3C-Cl}=3\cdot M{{CH}3}+M_C+M{Cl}=3\times\left(M_C+3\cdot M_H\right)+M_C+M{Cl}$$
A.N. : $M=3\times\left(12,0+3\times1,00\right)+12,0+35,5=92,5\ g/mol$
$$n_0=\frac{\rho\times V}{M}=\frac{0,850\times1,0}{92,5}=9,2\cdot{10}^{-3}\ mol$$

Q6. En déduire la valeur de la concentration en quantité de matière initiale en chlorure de tertiobutyle c₀ dans le mélange réalisé conformément au protocole.

$$C_0=\frac{n_0}{V+V_E}=\frac{9,2\cdot{10}^{-3}}{(1,0+200)\cdot{10}^{-3}}=4,6\cdot{10}^{-2}\ mol/L$$

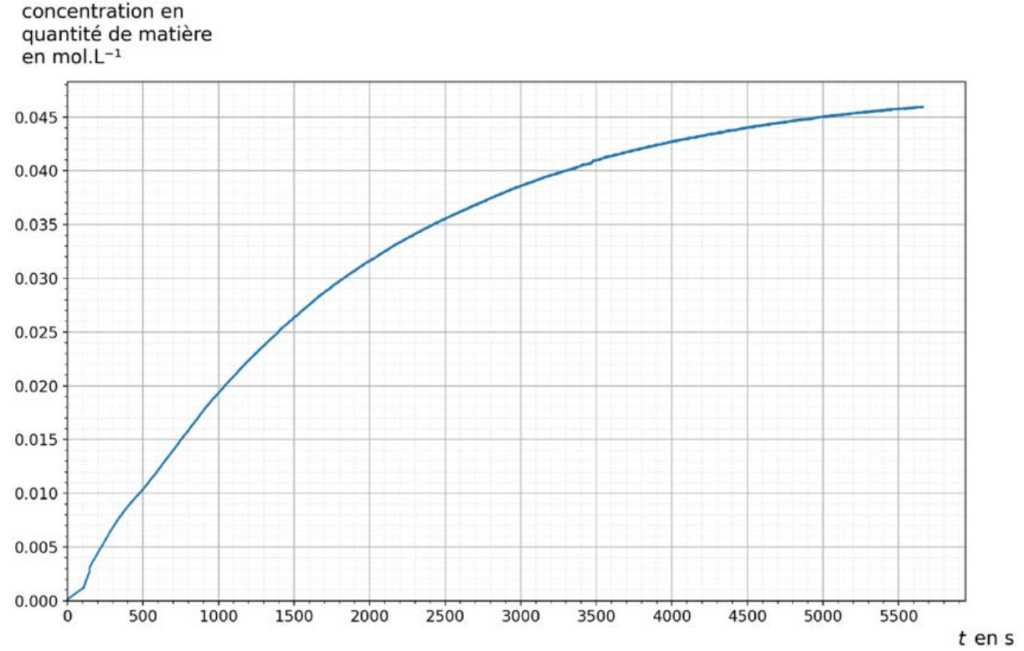
Les courbes représentant la concentration en quantité de matière en chlorure de tertiobutyle [RCℓ] et la concentration en quantité de matière en ions oxonium [H₃O⁺] en fonction du temps t sont données figure 2.

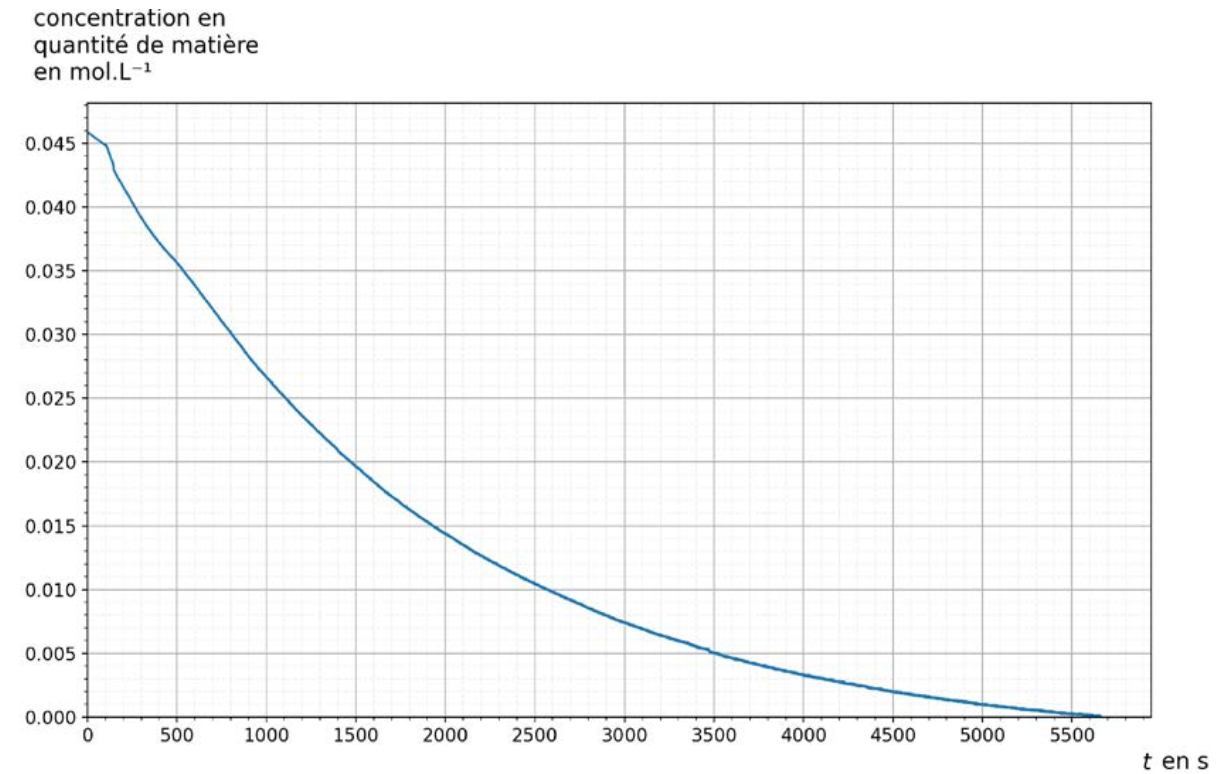
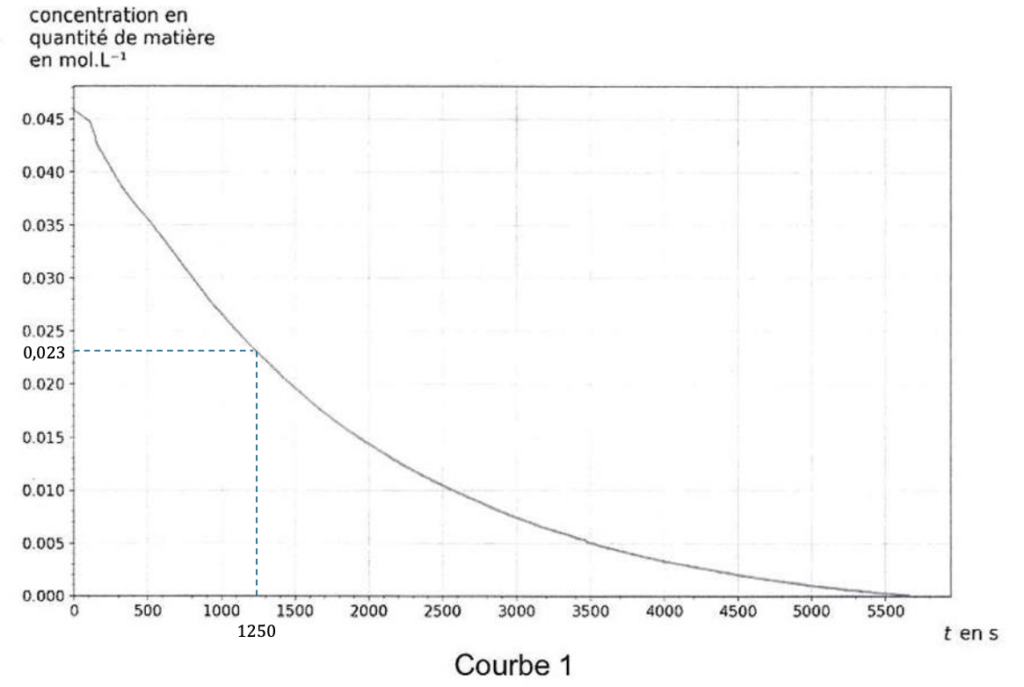
Courbe 1

Courbe 2

Figure 2. Représentations graphiques des variations des concentrations en quantité de matière [RCℓ] et [H₃O⁺] en fonction du temps.

Q7. Associer, en justifiant votre choix, chaque courbe 1 et 2 à chacune des espèces chimiques RCℓ et H₃O⁺.

D’après l’équation de réaction, RCl est un réactif et réagit avec l’eau, donc $[RCl]$ diminue, et c’est ce qu’on observe sur la courbe 1. Donc la courbe 1 montre l’évolution de la concentration de RCl dans la solution au cours du temps. ${H_3O}^+$ est un produit de la réaction, donc $[{H_3O}^+]$ augmente, et c’est ce qu’on observe sur la courbe 2. Donc la courbe 2 montre l’évolution de la concentration de ${H_3O}^+$ dans la solution au cours du temps.

Q8. À l’aide d’une des deux courbes, montrer que l’hydrolyse du chlorure de tertiobutyle est totale.

D’après la courbe 1, on voit que $\left[RCl\right]=0\ mol/L$ au bout de $t=5700\ s$ environ. Cela montre que les molécules de RCl ont tous réagi avec l’eau, et donc, que la réaction de l’hydrolyse du chlorure de tertiobutyle est totale.

Q9. Définir le temps de demi-réaction noté t_1/2 d’une transformation chimique.

Le temps de demi-réaction $t_{1/2}$ est la durée nécessaire au bout de laquelle la moitié du réactif limitant a disparu en ayant réagi. Et donc, sa quantité de matière a été divisée par 2.

Q10. Estimer graphiquement sa valeur t_1/2 à l’aide d’une des deux courbes de la figure 2.

Loi de vitesse.

Q11. Donner l’expression de la vitesse volumique de disparition v_RCℓ du chlorure de tertiobutyle.

La vitesse volumique de disparition du chlorure de tertiobutyle s’exprime par :
$$v_{RCl}=-dRCl/dt$$

Q12. Indiquer qualitativement comment évolue la vitesse volumique de disparition du chlorure de tertiobutyle v_RCℓ au cours du temps en justifiant votre réponse.

$v_{RCl}$ semble être rapide au début de la réaction (à $t=0\ s$), puis la vitesse ralentit après $t_{1/2}=1250\ s$ jusqu’à devenir lente après $t=3500\ s$.

Si la cinétique de la transformation est d’ordre 1 alors la vitesse volumique de disparition du chlorure de tertiobutyle peut également s’écrire : v_RCℓ (t) = k·[RCℓ]_(t) où k est une constante positive.

Q13. Donner l’allure de la courbe représentant la vitesse volumique de disparition du chlorure de tertiobutyle vRCℓ en fonction de la concentration en chlorure de tertiobutyle [RCℓ] en sachant que la réaction suit une loi d’ordre 1.

Si la réaction est une loi d’ordre 1, alors la courbe représentant $v_{RCl}$ en fonction de $\left[RCl\right]$ aurait l’allure d’une droite de pente positive passant par l’origine. Il y a donc proportionnalité entre $v_{RCl}$ et $\left[RCl\right]$.

Q14. Établir l’expression de l’équation différentielle du premier ordre vérifiée par [RCℓ](t).

On a $v_{RCl}=-\frac{d\left[RCl\right]{\left(t\right)}}{dt}$ et $v_{RCl}=k\cdot RCl$ ; donc $-\frac{d\left[RCl\right]{\left(t\right)}}{dt}=k\cdot [RCℓ]$
$$\frac{d\left[RCl\right]{\left(t\right)}}{dt}=-k\cdot [RCℓ]$$

La solution de l’équation différentielle est de la forme [RCℓ](t) = A· e^–k·t.

Q15. Déterminer la valeur de A à partir des conditions initiales de la transformation d’hydrolyse du chlorure de tertiobutyle.

On a donc $[RCℓ]=A\cdot e-k\cdot t$
Or, d’après les conditions initiales, on sait que $[RCℓ]=4,6\cdot10-2\ mol/L$
$$[RCℓ]=A\cdot e-k\times0=4,6\cdot 10-2\ mol/L$$
$$A\cdot e^0=A\times1=A=4,6\cdot {10}^{-2}\ mol/L$$
Donc la valeur de A est : $A=4,6\cdot {10}^{-2}\ mol/L$

Pour linéariser l’expression de la solution, on utilise la fonction logarithme népérien. La courbe représentant le logarithme népérien de la concentration en chlorure de tertiobutyle ln[RCℓ] en fonction du temps t est donnée figure 3.

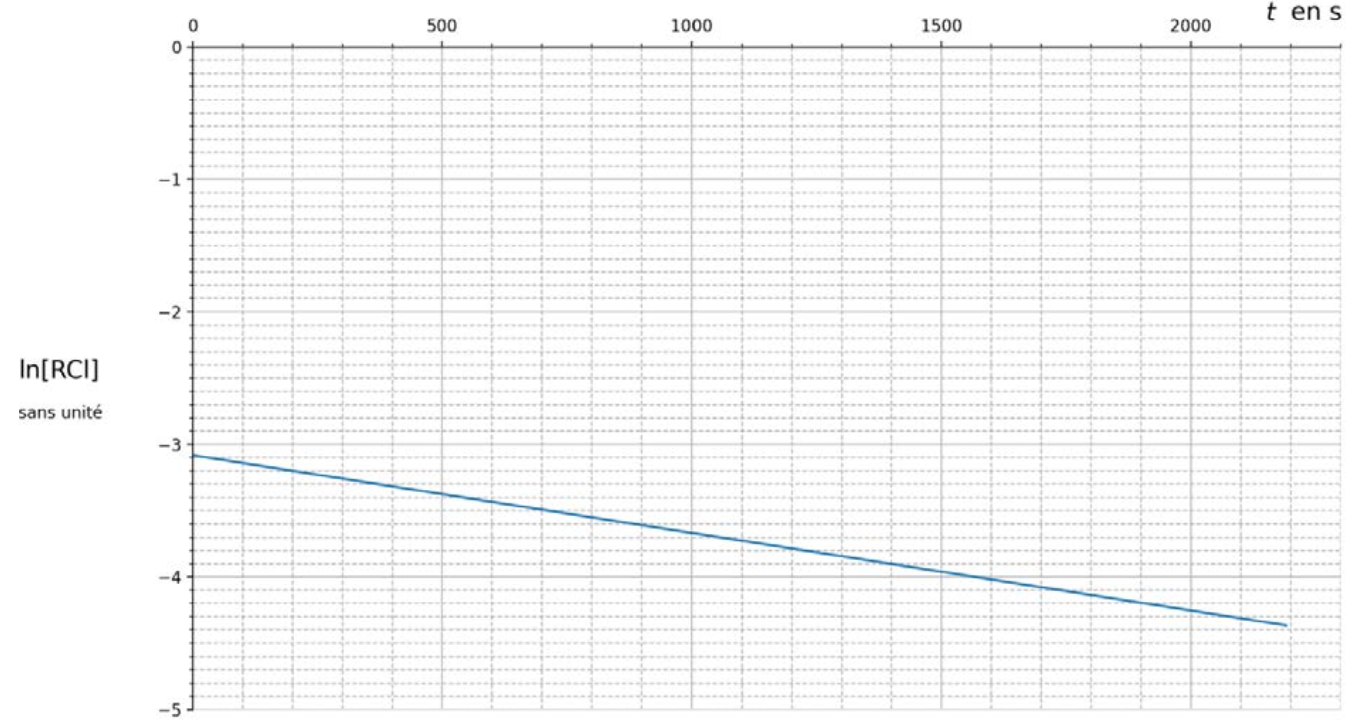
Figure 3. Représentation graphique des variations du logarithme népérien de la concentration en chlorure de tertiobutyle ln[RCℓ] en fonction du temps t.

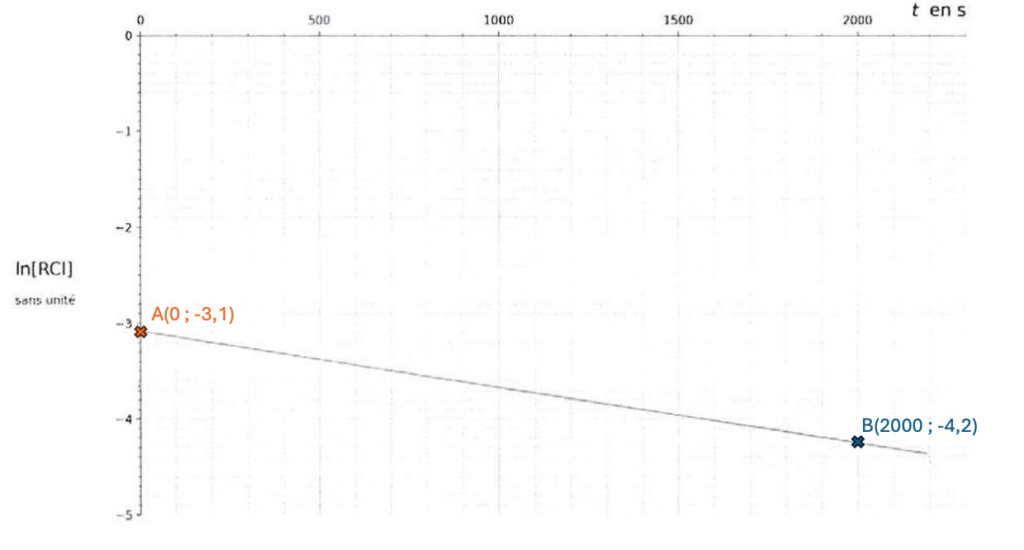
Q16. Calculer la valeur du coefficient directeur noté a de la droite obtenue.

Données :

• La valeur de k dans l’expression de la vitesse volumique de disparition du chlorure de tertiobutyle vRCℓ (t) = k·[RCℓ](t) est k = –a ;
• Le temps de demi-réaction noté t_1/2 s’exprime en fonction de k : $t_{1/2}=\frac{\ln 2}{k}$∙

Q17. À l’aide de l’expression précédente, calculer la valeur du temps de demi-réaction t_1/2 et comparer à la valeur obtenue à la question Q10.

$$k=-a=-\left(-5,5\cdot{10}^{-4}\right)=5,5\cdot{10}^{-4}\ s^{-1}$$
Or : $$t_{1/2}=\frac{\ln(2)}{k}$$
A.N. : $$t_{1/2}=\frac{\ln(2)}{5,5\cdot{10}^{-4}\ }=1260\ s.$$
Donc $t_{1/2}=1260\ s$.
On a donc une valeur plus précise et très proche de celle trouvée à la question Q10.