Centres étrangers 2022 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1G11
Sujet et corrigé
Mots-clés: Synthèse organique, spectroscopie IR, quotient de réaction, rendement
Du fait de son odeur fruitée, l’éthanoate d’octyle est un ester utilisé pour préparer des arômes artificiels, en particulier des arômes d’orange.

Cet exercice porte sur la synthèse de l’éthanoate d’octyle. Dans un premier temps, on détermine le rendement d’un protocole donné de synthèse de l’éthanoate d’octyle. Dans un second temps, on cherche à optimiser ce protocole afin d’augmenter le rendement.
Equation de la réaction de synthèse

Protocole simplifié de la synthèse de l’éthanoate d’octyle
Synthèse
Introduire, dans un ballon, une quantité 𝑛1 = 0,100 mol d’acide éthanoïque et 𝑛2 = 0,100 mol d’octan-1-ol.
Ajouter quelques grains de pierre ponce.
Adapter un réfrigérant à eau sur le ballon.
Chauffer à reflux à 40 °C pendant 2 heures.
Après chauffage, laisser refroidir jusqu’à température ambiante.
Traitement du milieu réactionnel
Ajouter, par le haut du réfrigérant, 50 mL d’une solution aqueuse d’hydrogénocarbonate de sodium.
Transvaser le contenu du ballon dans une ampoule à décanter.
Extraire la phase organique.
Données :
- Sur les espèces chimiques mises en jeu
| Espèce chimique | Acide éthanoïque | Octan-1-ol | Ethanoate d’octyle |
|---|---|---|---|
| Formule brute | C2H4O2 | C8H18O | C10H20O2 |
| Représentation topologique | 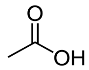 | 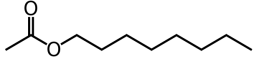 |
|
| Solubilité en solution aqueuse | Totale | Faible | Très faible |
| Masse molaire | 60,0 g·mol-1 | 130 g·mol-1 | 172 g·mol-1 |
- Table de données de spectroscopie infrarouge
| Liaison | O – H | C = O |
| Nombres d’onde (en cm-1) | 3 200 à 3 500 | 1 650 à 1 740 |
| Intensité du pic | Forte | Forte |
| Largeur du pic | Large | Fine |
Rendement de la synthèse
Une première analyse de la phase organique obtenue après la synthèse est faite par chromatographie sur couche mince (CCM). Celle-ci révèle la présence de deux espèces chimiques. Une séparation est réalisée. Deux liquides, A et B, de masse respective 𝑚𝐴 = 4,30 g et 𝑚𝐵 = 11,34 g sont obtenus.
Leurs spectres IR sont donnés ci-dessous :
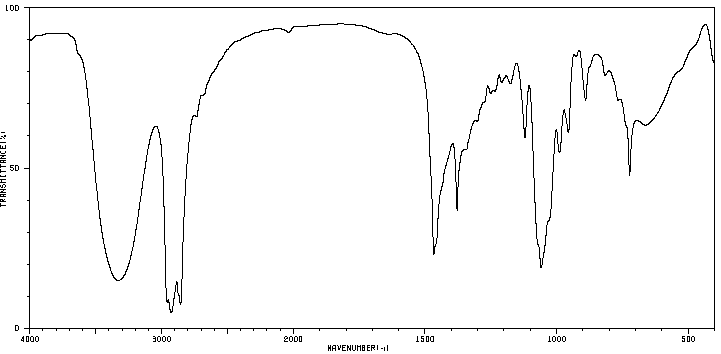
Spectre du liquide A
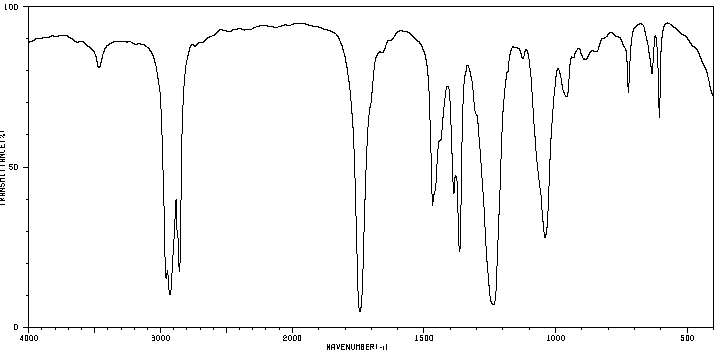
https://sdbs.db.aist.go.jp/sdbs/cgi-bin/direct_frame_top.cgi
1. Expliquer l’intérêt d’ajouter une solution aqueuse dans le milieu réactionnel avant de procéder à la séparation par décantation (comme indiqué dans la partie « traitement du milieu réactionnel » du protocole).
Dans l’étape de séparation nous voulons récupérer le produit ethanoate d’octyle. L’ethanoate d’octyle est très faiblement soluble dans une solution aqueuse. Ainsi l’ajout de la solution aqueuse permet d’extraire l’ethanoate d’octyle.
2. Identifier, en justifiant, les espèces chimiques pouvant être présentes dans la phase organique.
Les espèces pouvant être présente dans la phase organique sont celle qui sont faiblement solubles dans la solution aqueuse :
- Octan-1-ol (réactif restant si la réaction n’est pas totale)
- Ethanoate d’octyle
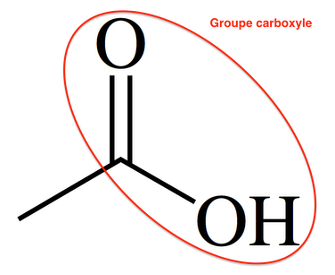
3. Recopier et nommer les groupes fonctionnels présents dans les molécules d’acide éthanoïque et d’éthanoate d’octyle.
Groupe carboxyle
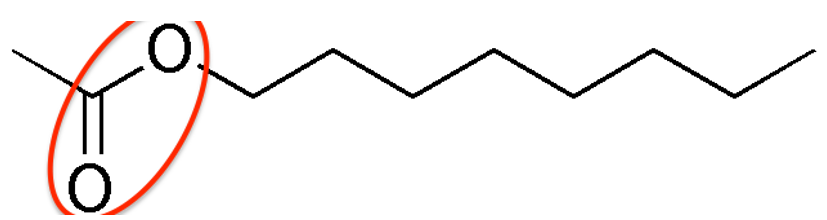
Groupe ester
4. À l’aide des deux spectres, montrer que le liquide A correspond à l’alcool et le liquide B à l’ester.

L’alcool (liaison 0-H) présente une bande entre 3200 et 3500 cm-1.
Elle est présente dans le spectre A :
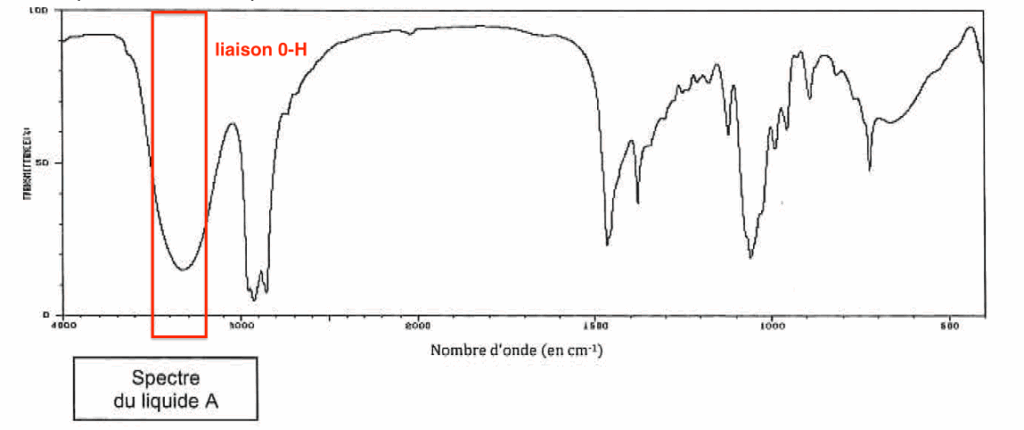
L’ester (liaison C=O) présente une bande entre 1650 et 1740 cm-1 . Elle est présente dans le spectre B :
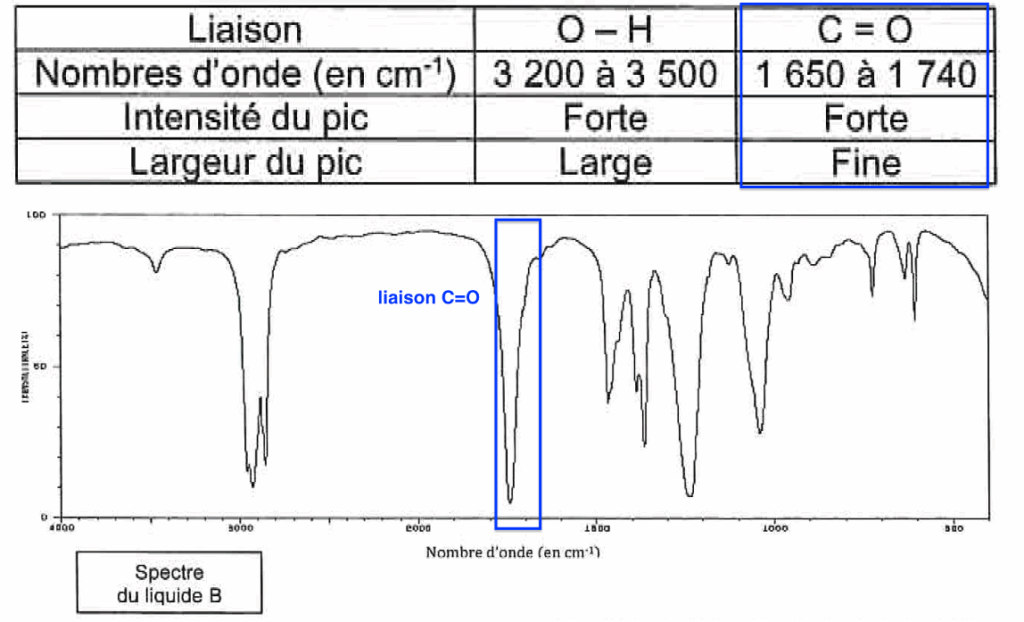
5 Déterminer les quantités de matière en octan-1-ol et en éthanoate d’octyle obtenues.
$$n_{Octan-1-ol}=n_A$$
$$n_{Octan-1-ol}=\frac{m_A}{M_A}$$
$$n_{Octan-1-ol}=\frac{4,30}{130}$$
$$n_{Octan-1-ol}=3,3\times10^{-2}\ mol$$
$$n_{\text{Éthanoate d’octyle}}=n_B$$
$$n_{\text{Éthanoate d’octyle}}=\frac{m_B}{M_B}$$
$$n_{\text{Éthanoate d’octyle}}=\frac{11,34}{172}$$
$$n_{\text{Éthanoate d’octyle}}=6,59\times10^{-2}\ mol$$
Le rendement de la synthèse est défini par :
$\eta = \frac{n(C_{10}H_{20}O_{2})_f}{n(C_{10}H_{20}O_{2})_{max}}$
où 𝑛(𝐶10𝐻20𝑂2)𝑓 représente la quantité de matière d’éthanoate d’octyle à l’état final, à l’équilibre, et 𝑛(𝐶10𝐻20𝑂2)𝑚𝑎𝑥 la quantité de matière d’éthanoate d’octyle si la réaction était totale.
6. Calculer le rendement de cette synthèse.
$$\eta=\frac{n_{(C_{10}H_{20}O_2)f}}{n_{(C_{10}H_{20}O_2)max}}$$
$n_{(C_{10}H_{20}O_2)f}=n_{\text{Éthanoate d’octyle}}=6,59\times10^{-2}\ mol$
$n_{(C_{10}H_{20}O_2)max}=x_{max}=0,100\ mol$
$$\eta=\frac{n_{(C_{10}H_{20}O_2)f}}{n_{(C_{10}H_{20}O_2)max}}$$
$$\eta=\frac{6,59\times10^{-2}}{0,100}$$
$$\eta=0,659$$
$$\eta=65,9%$$
Optimisation de la synthèse
Durant la synthèse, avant la séparation des deux phases, le quotient de réaction peut être exprimé en fonction des quantités de matière des espèces suivant la relation :
$Q_r = \frac{n(C_{10}H_{20}O_{2}) \times n(H_{2}O) }{n(C_{2}H_{4}O_{2}) \times n(C_{8}H_{18}O)}$
Données :
- La constante d’équilibre de la réaction de synthèse vaut 𝑄𝑟,é𝑞 = 𝐾 = 4,0.
- Avec un mélange équimolaire initial en acide et en alcool, le rendement de cette réaction de synthèse a pour valeur : 𝜂 = 66 %.
Afin d’augmenter le taux d’avancement de la synthèse, on introduit un réactif en excès.
7. En raisonnant sur le quotient de réaction, expliquer pourquoi l’ajout d’un réactif permet de déplacer l’équilibre.
$$Q_r=\frac{n_{(C_{10}H_{20}O_2)}\times n_{(H_2O)}}{n_{(C_2H_4O_2)}\times n_{(C_8H_{18}O)}}$$
En ajoutant un réactif, $n_{(C_2H_4O_2)}$ ou $n_{(C_8H_{18}O)}$ augmente.
Ainsi $Q_r$ diminue car il est inversement proportionnel aux quantités de matière des réactifs.
$Q_r$ devient inférieur à $K$ : la réaction a lieu dans le sens direct.
On note :
- 𝑛’1 la nouvelle quantité d’acide éthanoïque initiale ;
- pour rappel, 𝑛2 , la quantité d’octan-1-ol initiale (𝑛2 = 0,100 mol) ;
- 𝑥é𝑞 l’avancement de la réaction à l’équilibre.
On admet que le quotient de réaction dans l’état d’équilibre du système peut s’exprimer sous la forme :
$Q_{r,èq} = \frac{x_{eq}^2}{(n’_1-x_{eq}) \times (n_2-x_{eq})}$
8. Déterminer la quantité 𝑛′ d’acide éthanoïque à introduire pour obtenir un rendement d’au moins 0,95.
$$x_{max}=n_{\text{réactif limitant}}=n_2=0,100\ mol$$
Le rendement :
$$\eta=\frac{x_{eq}}{x_{max}}$$
On souhaite un rendement de $0,95$. Ainsi :
$$x_{eq}=\eta\times x_{max}$$
$$x_{eq}=0,95\times0,100$$
$$x_{eq}=9,5\times10^{-2}\ mol$$
$$Q_{r,eq}=\frac{x_{eq}^2}{(n_1^\prime-x_{eq})\times(n_2-x_{eq})}$$
$$Q_{r,eq}=\frac{(9,5\times10^{-2})^2}{(n_1^\prime-9,5\times10^{-2})\times(0,100-9,5\times10^{-2})}$$
$$4,0=\frac{9,0\times10^{-3}}{(n_1^\prime-9,5\times10^{-2})\times5,0\times10^{-3}}$$
$$4,0\times(n_1^\prime-9,5\times10^{-2})\times5,0\times10^{-3}=9,0\times10^{-3}$$
$$2,0\times10^{-2}\times(n_1^\prime-9,5\times10^{-2})=9,0\times10^{-3}$$
$$(n_1^\prime-9,5\times10^{-2})=\frac{9,0\times10^{-3}}{2,0\times10^{-2}}$$
$$(n_1^\prime-9,5\times10^{-2})=0,45$$
$$n_1^\prime=0,45+9,5\times10^{-2}$$
$$n_1^\prime=0,545\ mol$$
Pour obtenir un rendement au moins égal à $0,95$, il faut introduire $n_1^\prime\geq0,545\ mol$.
