Nouvelle Calédonie 2025 Sujet 2

Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée

Sujet n°25-PYCJ2NC1

EXERCICE I – SYNTHÈSE D’UN ÉDULCORANT : L’ASPARTAME (9 points)

L’aspartame remplace le sucre dans des régimes hypocaloriques. Il est synthétisé à partir d’acide aspartique et de phénylalanine méthylée.

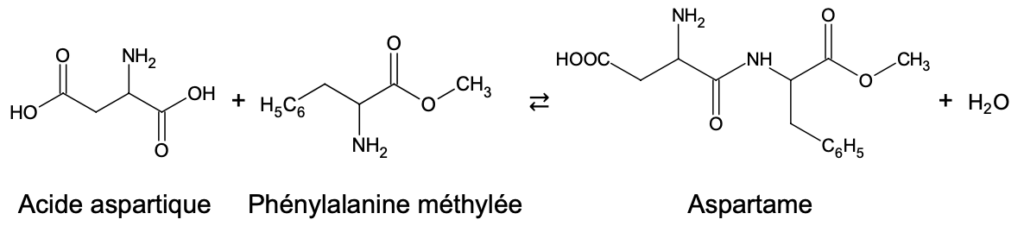
Figure 1 – Équation de réaction de formation de l’aspartame

L’objet de cet exercice est d’étudier les propriétés acido-basiques des espèces chimiques intervenant dans la synthèse de l’aspartame, puis la stratégie à envisager pour le synthétiser.

Les parties A, B et C de cet exercice sont indépendantes et peuvent être traitées séparément.

Données :

L’acide aspartique existe en solution aqueuse sous quatre formes que l’on note : H₃Asp⁺, H₂Asp, HAsp⁻ et Asp^2–.
Les valeurs des pK_A des couples acide-base de ces quatre formes sont :

pK_A1	pK_A2	pK_A3
1,9	?	9,6

Extrait du diagramme de distribution :

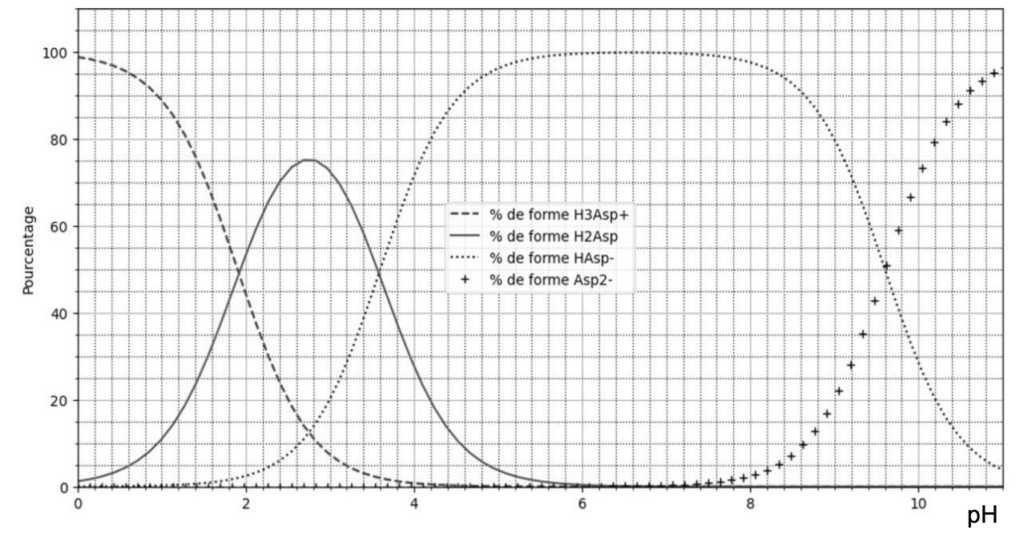
Figure 2 – Diagramme de distribution de l’acide aspartique sous ses formes H₃Asp⁺, H₂Asp, HAsp⁻ et Asp^2–

La formule topologique de H₂Asp en solution aqueuse est :

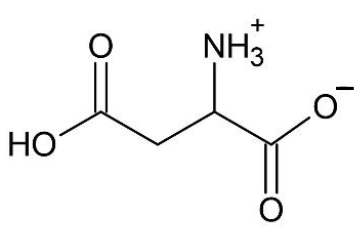
M(H₂Asp) = 133 g∙mol^–1.
Produit ionique de l’eau : 𝐾_𝑒 = 1,0 × 10^–14.
Couple acide-base : H2O(𝓁) /HO^–(aq).
Concentration standard : c ^॰ = 1,0 mol∙L^–1.
Électronégativités selon Pauling : χ(H) = 2,20 ; χ(C) = 2,55 ; χ(N) = 3,00 et χ(O) = 3,44.

Partie A – L’acide aspartique

1. Tracer le diagramme de prédominance de l’acide aspartique et faire apparaître les quatre formes associées.

Diagramme de prédominance :

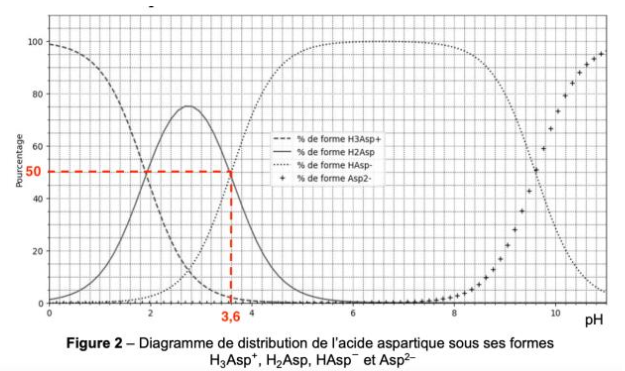
2. Déterminer, en justifiant, la valeur de pK_A2 .

Lorsque $\left[H_2Asp\right]{eq}=\left[{\rm HAsp}^-\right]{eq}$
$$pH={\rm pK}_{A2}$$

Graphiquement $\left[H_2Asp\right]{eq}=\left[{\rm HAsp}^-\right]{eq}$ pour $pH=3,6$
Ainsi, ${\rm pK}_{A2}=3,6$

3. Justifier que H₂Asp est une espèce amphotère.

L’espèce chimique H₂Asp est la base du couple : H₃Asp⁺ / H₂Asp
L’espèce chimique H₂Asp est l’acide du couple : H₂Asp / HAsp⁻
Ainsi, l’espèce chimique H₂Asp est une espèce amphotère.

4. Sachant que le pK_A d’un acide carboxylique est inférieur au pK_A d’une amine, représenter la formule topologique de HAsp⁻ correspondant à la perte d’un proton sur la molécule H₂Asp.

H₂Asp :

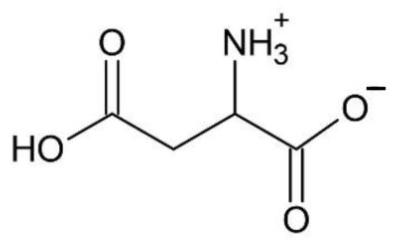
D’après le sujet : « le pK_A d’un acide carboxylique est inférieur au pK_A d’une amine »
Ainsi, le groupement le plus acide est celui d’un carboxyle : c’est donc COOH qui perd le proton H⁺ en premier, tandis que l’amine garde son proton H⁺.

HAsp⁻ :

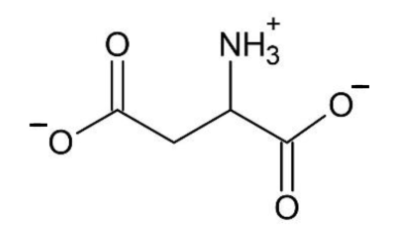
Titrage pH-métrique de l’acide aspartique

On souhaite déterminer la masse d’acide aspartique contenue dans un échantillon du commerce dont la masse est de 250 mg.

On dissout la totalité de l’échantillon dans 100 mL d’eau distillée sans variation de volume. Le pH de la solution au début de l’expérience vaut 2,8. Le titrage est effectué en introduisant des volumes de solution aqueuse d’hydroxyde de sodium (Na⁺(aq) + HO^–(aq)) de concentration en quantité de matière C_b = 0,100 mol∙L^–1. On verse un volume maximal de réactif titrant de 17,5 mL.

5. Justifier la forme prédominante de l’acide aspartique dans la solution au début du titrage.

Le pH de la solution au début de l’expérience vaut 2,8
Diagramme de prédominance :

Pour pH=2,8 H₂Asp est prédominant

6. Réaliser le schéma légendé du montage mis en œuvre pour réaliser le titrage.

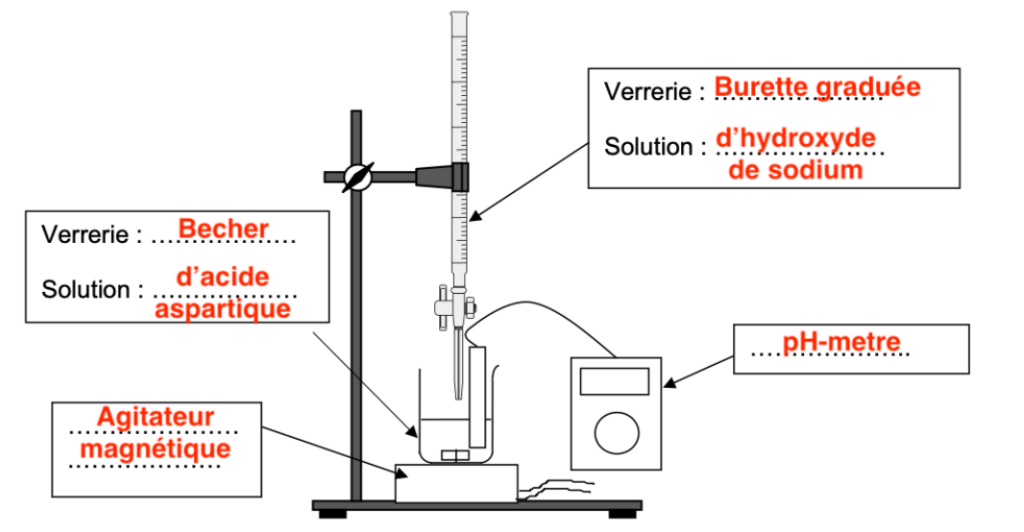
L’équation de la réaction support du titrage mis en œuvre s’écrit :

H₂Asp(aq) + HO⁻(aq) → HAsp⁻(aq)+ H₂O(𝓁)

7. Définir l’équivalence.

L’équivalence est atteinte lorsque les réactifs sont introduits dans les proportions stœchiométriques.

La courbe du titrage est donnée sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11.

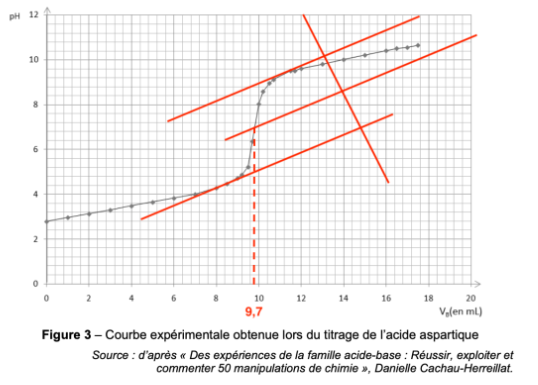
8. Déterminer graphiquement, à l’aide de la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, la valeur du volume équivalent V_E de solution d’hydroxyde de sodium.

On détermine graphiquement le volume à l’équivalence avec la méthode des tangentes parallèles : $V_E=9,7\ mL$

9. Calculer la valeur de la masse d’acide aspartique contenue dans l’échantillon.

$$H_2Asp(aq)+{\rm HO}^-\left(aq\right)\rightarrow{\rm HAsp}^-\left(aq\right)+H_2O\left(l\right)$$
A l’équivalence :
$$\frac{n_{H_2Asp}^i}{1}=\frac{n_{{\rm HO}^-}^{eq}}{1}$$

$$n(H_2Asp)=n_e({\rm HO}^-)$$

$$\frac{m(H_2Asp)}{M(H_2Asp)}=C_B\times V_E$$
$$m(H_2Asp)=C_B\times V_E\times M(H_2Asp)$$
$$m(H_2Asp)=0,100\times 9,7\times{10}^{-3}\times 133$$
$$m(H_2Asp)=0,13\ g$$
Calculer la valeur de la masse d’acide aspartique contenue dans l’échantillon est de 0,13 g.

Partie B – Étude de la phénylalanine méthylée

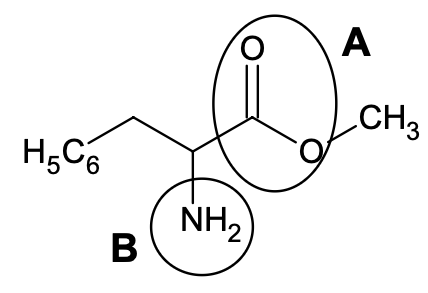
Figure 4 – Formule topologique de la phénylalanine méthylée

10. Nommer les groupes caractéristiques A et B entourés sur la figure 4. Pour la suite de l’exercice, on note la phénylalanine méthylée R-N̅H₂.

Groupe caractéristique A : Carboxyle (non demandé : famille des ester)
Groupe caractéristique B : Amine (non demandé : famille des Amine).

11. Justifier, à partir de la structure de R-N̅H₂, son caractère basique au sens de Brønsted.

Une base est une espèce capable de capter un proton H⁺.
$R-\bar{N}H_2$ est une capable de capter un proton H⁺ : $R-\bar{N}H_2$ est une base au sens de Brønsted.

12. En déduire la formule de l’acide conjugué de R-N̅H₂.

$R-\bar{N}H_2$ est une capable de capter un proton H⁺ pour devenir $R-NH_3^+$.
Ainsi, l’acide conjugué de $R-\bar{N}H_2$ est $R-NH_3^+$.

13. Établir l’équation de la réaction de la phénylalanine méthylée avec l’eau.

Équation de la réaction de la phénylalanine méthylée avec l’eau.
$$R-\bar{N}H_2(aq)+H_2O(l)\rightleftarrows R-NH_3^+(aq)+{\rm HO}^-\left(aq\right)$$

Soit un volume V = 1,00 L d’une solution S de phénylalanine méthylée de concentration en quantité de matière c = 1,00 × 10^–1 mol∙L^–1. Le pH de cette solution est égal à 12,9.

14. Calculer le taux d’avancement final 𝜏 et conclure sur la force de la base, la phénylalanine méthylée.

Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche pertinente, même non aboutie, sera valorisée.

Construisons un tableau d’avancement :
$$n_{R-\bar{N}H_2}^i=C\times V$$

	$$R-\bar{N}H_2(aq)$$	$$+H_2O(l)\rightleftarrows$$	$$R-NH_3^+(aq)$$	$$+\ {\rm HO}^-\left(aq\right)$$
État initial	$$C\times V$$	Solvant	0	0
État intermédiaire	$$C\times V-x$$	Solvant	$$x$$	$$x$$
État final	$$C\times V-x_f$$	Solvant	$$x_f$$	$$x_f$$

$$\tau=\frac{x_f}{x_{max}}$$

Trouvons $x_{max}$ :
$$C\times V-x_{max}=0$$
$$x_{max}=C\times V$$

Trouvons $x_f$ :
$$n_{{\rm HO}^-}^f=x_f$$
$$x_f=n_{{\rm HO}^-}^f$$
$$x_f=\left[{\rm HO}^-\right]_{eq}\times V$$

$$K_e=\frac{\left[H_3O^+\right]{eq}\times\left[{\rm HO}^-\right]{eq}}{{{(c}^0)}^2}$$
$$\frac{\left[H_3O^+\right]{eq}\times\left[{\rm HO}^-\right]{eq}}{{{(c}^0)}^2}=K_e$$
$$\left[{\rm HO}^-\right]{eq}=\frac{K_e\times{{(c}^0)}^2}{\left[H_3O^+\right]{eq}}$$

D’où
$$x_f=\frac{K_e\times{{(c}^0)}^2}{\left[H_3O^+\right]_{eq}}\times V$$

Or $\left[H_3O^+\right]_{eq}=c^0\times{10}^{-pH}$

D’où
$$x_f=\frac{K_e\times{{(c}^0)}^2}{c^0\times{10}^{-pH}}\times V$$
$$x_f=\frac{K_e\times c^0}{{10}^{-pH}}\times V$$

$$\tau=\frac{x_f}{x_{max}}$$
$$\tau=\frac{\frac{K_e\times c^0}{{10}^{-pH}}\times V}{C\times V}$$
$$\tau=\frac{\frac{K_e\times c^0}{{10}^{-pH}}}{C}$$
$$\tau=\frac{K_e\times c^0}{C{\times10}^{-pH}}$$
$$\tau=\frac{{1,0\times 10}^{-14}\times 1,0}{1,0\times{10}^{-1}\times{10}^{-12,9}}$$
$$\tau=0,79$$
$$\tau=79%$$

Le taux d’avancement final $\tau$ de cette réaction est de 79%.

Partie C – Stratégie de synthèse

On souhaite créer une liaison entre l’acide aspartique et la phénylalanine méthylée pour obtenir l’aspartame selon l’équation de réaction donnée figure 1 en début d’exercice.

15. Identifier en expliquant, parmi les catégories suivantes, celle à laquelle appartient cette transformation : oxydoréduction, acide-base, addition, élimination, substitution.

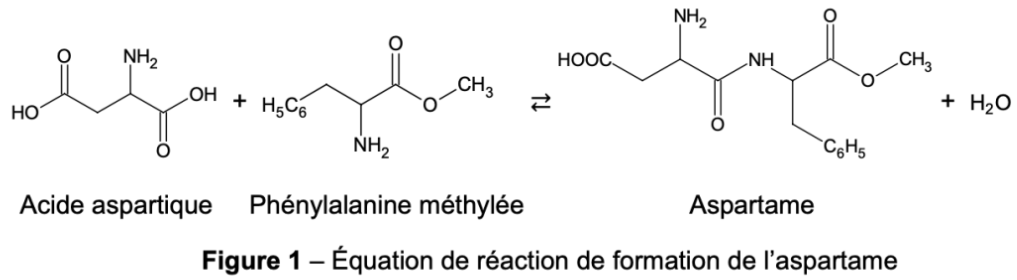
Lors de la formation de l’aspartame, la fonction acide carboxylique réagit avec fonction amine et il se forme une liaison amide.
La transformation représentée correspond à une réaction de substitution.

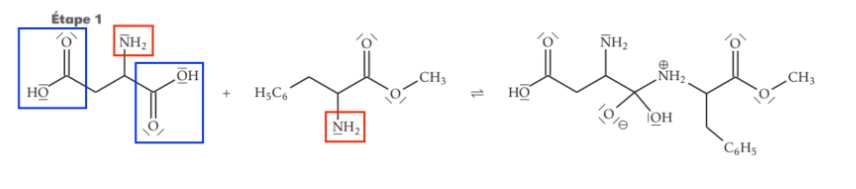
16. Sur l’étape 1 de la figure 5 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, faire apparaître les sites donneurs et accepteurs de doublet d’électrons des réactifs impliqués lors de la synthèse.

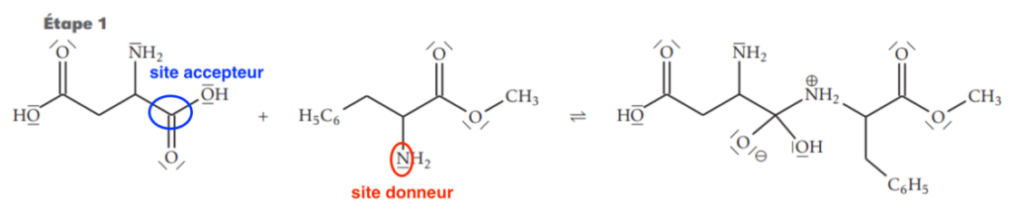
17. Représenter, sur l’étape 1 de la figure 5 de l’ANNEXE À RENDRE AVEC LA COPIE page 11/11, les flèches courbes de l’acte élémentaire correspondant à l’obtention de l’intermédiaire réactionnel.

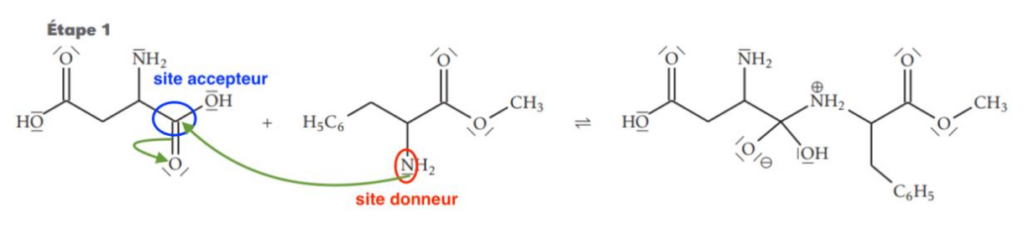
Lors d’une formation de liaison, le doublet d’électrons se déplace du site donneur vers un site accepteur.
Lors d’une rupture de liaison, la flèche part de la liaison vers l’atome le plus électronégatif.

18. Identifier, en justifiant, l’intermédiaire réactionnel de cette synthèse.

L’intermédiaire réactionnel est le produit formé à la fin de l’étape 1 puis consommé en étape 2.

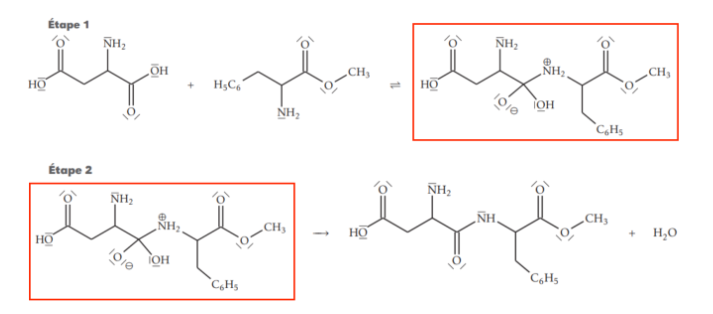
L’intermédiaire réactionnel de cette synthèse est :

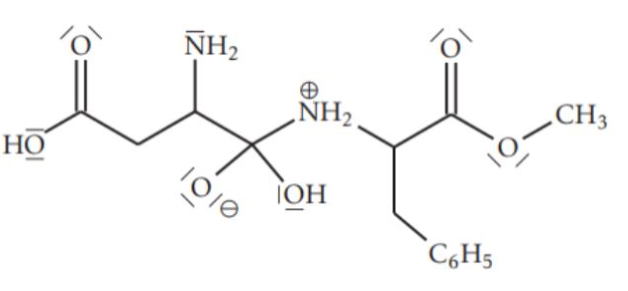
19. Justifier que d’autres intermédiaires réactionnels sont susceptibles de se former.

La fonction acide carboxylique réagit avec fonction amine et il se forme une liaison amide.
Or il n’y a pas qu’une fonction acide carboxylique et une fonction amine.
Ainsi, d’autres réactions entre un acide carboxylique et une fonction amine que celle de l’étape 1 peut avoir lieu.
C’est pourquoi d’autres intermédiaires réactionnels sont susceptibles de se former.

20. Proposer une stratégie à adopter pour s’assurer de la formation de l’aspartame uniquement.

Pour s’assurer de la formation de l’aspartame uniquement, il faut :
• Protéger la fonction acide carboxylique et la fonction amine qu’on ne souhaite pas voir réagir
• Faire la réaction désirée
• Déprotéger ensuite la fonction acide carboxylique et la fonction amine qui avaient été protégé

ANNEXE À RENDRE AVEC LA COPIE

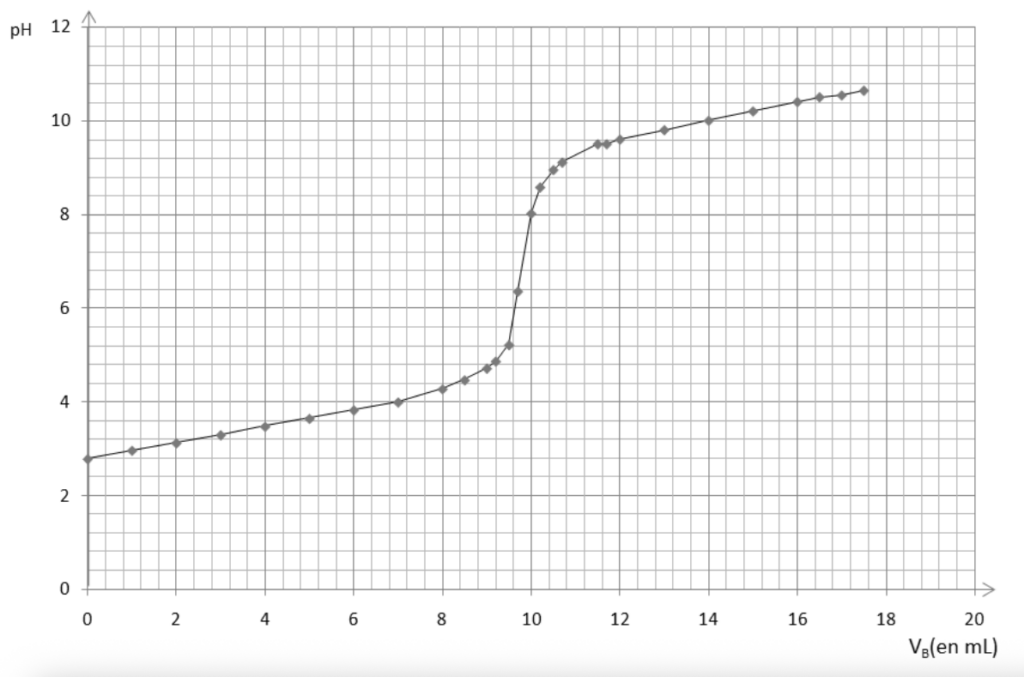
Figure 3 – Courbe expérimentale obtenue lors du titrage de l’acide aspartique

Source : d’après « Des expériences de la famille acide-base : Réussir, exploiter et commenter 50 manipulations de chimie », Danielle Cachau-Herreillat.

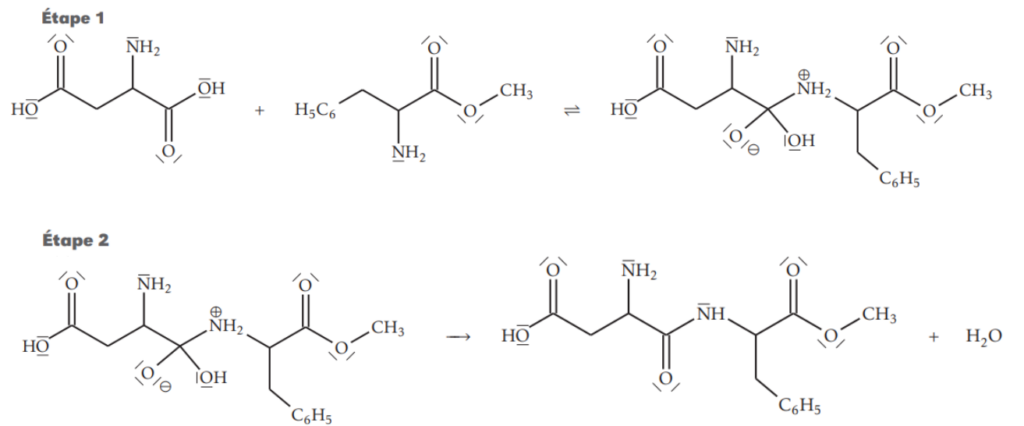
Figure 5 – Mécanisme réactionnel simplifié de la synthèse de l’aspartame